Im Gegensatz zu Dreiecksungleichungen bei Halbnormen, -Halbnormen oder der Subadditivität mit Stetigkeitskonstante der Addition bei Quasihalbnormen kann man im Allgemeinen bei mehreren Summanden bei topologischen Algebren für mehrere Summanden in einer Addition nicht notwendig das gleiche Gaugefunktional unabhängig von der Anzahl der Summanden wählen. Das Kaskaden-Lemma für Summen ist notwendig, um für die Stetigkeit der Cauchy-Multiplikation und eine unterschiedliche Anzahl der Summanden ein Abschätzung zu erhalten, die die Cauchy-Multiplikation stetig auf der Polynomalgebra macht.
-Halbnormen oder der Subadditivität mit Stetigkeitskonstante der Addition bei Quasihalbnormen kann man im Allgemeinen bei mehreren Summanden bei topologischen Algebren für mehrere Summanden in einer Addition nicht notwendig das gleiche Gaugefunktional unabhängig von der Anzahl der Summanden wählen. Das Kaskaden-Lemma für Summen ist notwendig, um für die Stetigkeit der Cauchy-Multiplikation und eine unterschiedliche Anzahl der Summanden ein Abschätzung zu erhalten, die die Cauchy-Multiplikation stetig auf der Polynomalgebra macht.
Kaskadierende Summe mit Gaugefunktionalen
[Bearbeiten]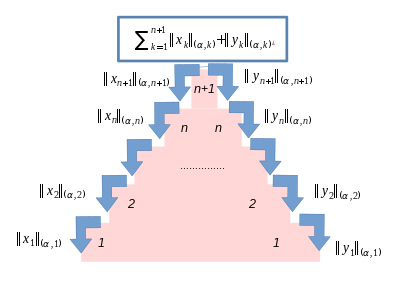
Sei  eine topologische Algebra mit dem basiserzeugenden
eine topologische Algebra mit dem basiserzeugenden  -Gaugefunktionalsystem
-Gaugefunktionalsystem  , dann gibt es für alle
, dann gibt es für alle  eine Stetigkeitssequenz
eine Stetigkeitssequenz  , die folgende Eigenschaften besitzt:
, die folgende Eigenschaften besitzt:
- (KA1)
 für
für  und
und 
- (KA2)

Für den Beweis verwendet man Ungleichung für die Stetigkeit der Addition für ein basiserzeugendes Gaugefunktionalsystem aus dem Topologisierungslemma für Algebren. Der Beweis gliedert sich in 3 Teile:
- Stetigkeitssequenz wird induktiv definiert,
- (KA1) Isotonie der Stetigkeitssequenz
- (KA2) Kaskadenungleichung
Mit der Stetigkeitssequenzen der Multiplikation erzeugen, d.h. es gibt zu jedem Gaugefunktional  ein
ein  mit
mit

für alle  . Zu
. Zu  gilt es wieder ein
gilt es wieder ein  -Gaugefunktional
-Gaugefunktional  mit
mit

für alle  . Man definiert nun
. Man definiert nun  .
.
Ist nun  gegeben, so kann man wieder zu diesem
gegeben, so kann man wieder zu diesem  -Gaugefunktional
-Gaugefunktional  wieder
wieder  finden, für das dann wiederum die folgende Ungleichung gilt:
finden, für das dann wiederum die folgende Ungleichung gilt:
 für alle
für alle 
- Man definiert nun

Beweis 3 - Abschätzung von Summen mit 4 Summanden
[Bearbeiten]Mit der obigen Konstruktion kann man Summen mit 4 Summanden wie folgt abschätzen:

Beweis 4 - Abschätzung von Summen mit 3 Summanden
[Bearbeiten]Mit der obigen Konstruktion kann man Summen kann man auch für 2 oder 3 Summanden anwenden, indem man einzelne Vektoren als Nullvektoren definiert. Im weiteren Verlauf wird die Abschätzung lediglich für 3 Summanden für das Kaskadenlemma benötigt und man setzt  .
.

Beweis 5 - (KA1) Isotonie der Stetigkeitssequenz
[Bearbeiten]Die Stetigkeitssequenz von Gaugefunktionalen ist isoton (d.h.  ), denn für alle
), denn für alle  gilt:
gilt:

Beweis 6 - (KA2) - Kaskadenungleichung
[Bearbeiten]Die Stetigkeitssequenz von Gaugefunktionalen wird schrittweise für 3 Summanden angewendet:

Insgesamt folgt die Behauptung. 
Sei  eine topologische Algebra mit dem basiserzeugenden
eine topologische Algebra mit dem basiserzeugenden  -Gaugefunktionalsystem
-Gaugefunktionalsystem  , dann gibt es für alle
, dann gibt es für alle  eine isotone Stetigkeitssequenz
eine isotone Stetigkeitssequenz  , die folgende Eigenschaften besitzt:
, die folgende Eigenschaften besitzt:
- (KA1)
 für
für  und
und 
- (KA2)
 für alle
für alle  .
.
Sei  eine topologische Algebra mit dem basiserzeugenden
eine topologische Algebra mit dem basiserzeugenden  -Gaugefunktionalsystem
-Gaugefunktionalsystem  , dann gibt es für alle
, dann gibt es für alle  eine isotone Stetigkeitssequenz
eine isotone Stetigkeitssequenz  , die folgende Eigenschaften besitzt:
, die folgende Eigenschaften besitzt:
- (SA1)
 für
für  und
und 
- (SA2)

Das Korollar 2 erhält man unmittelbar aus Korollar 1 durch Setzung von  .
.
Beweisen Sie das Korollar 1 unter Verwendung der Lemmas über Kaskadensummen und über die Stetigkeit der Multiplikation in einer topologischen Algebra (siehe Topologisierungslemma für Algebren)
Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.
Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Topologische Invertierbarkeitskriterien' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.




































