Laurent-Reihe

Einleitung

Die Laurent-Reihe (nach Pierre Alphonse Laurent) ist eine unendliche Reihe ähnlich einer Potenzreihe, aber zusätzlich mit negativen Exponenten. Allgemein hat eine Laurent-Reihe in ${\textstyle x}$ mit Entwicklungspunkt ${\textstyle c}$ diese Gestalt:

f(x)=\sum _{n=-\infty }^{\infty }c_{n}(x-a)^{n}

${\textstyle c_{n}}$ Koeffizienten
${\textstyle a}$ Entwicklungspunkt der Reihe

Hauptteil und Nebenteil

Die Reihe der Terme mit negativen Exponenten nennt man den Hauptteil der Laurent-Reihe, die Reihe der Terme mit nichtnegativen Exponenten nennt man den Nebenteil oder den regulären Teil.

Zusammenhang Potenzreihen

Eine Laurent-Reihe mit verschwindendem Hauptteil ist eine Potenzreihe; hat sie außerdem nur endlich viele Terme, dann ist sie ein Polynom. Hat eine Laurent-Reihe insgesamt nur endlich viele Terme (mit negativem oder positivem Exponent), dann nennt man sie ein Laurent-Polynom.

Geschichte

Die Laurent-Reihe wurde 1843 von dem französischen Mathematiker Pierre Alphonse Laurent vorgestellt. Aufzeichnungen im Nachlass des deutschen Mathematikers Karl Weierstraß deuten jedoch darauf hin, dass dieser sie bereits 1841 entdeckt hatte.

Laurent-Zerlegung

Das Prinzip der Entwicklung einer holomorphen Funktion in eine Laurent-Reihe basiert auf der Laurent-Zerlegung. Dazu betrachte man ein Kreisringgebiet ${\mathcal {R}}=\{z\in \mathbb {C} \;|\;r<|z|<R\}$ . Nun definiere man zwei holomorphe Funktionen $g$ und $h$ :

g\colon U_{R}(0)\rightarrow \mathbb {C}

h\colon U_{\frac {1}{r}}(0)\rightarrow \mathbb {C}

.

Darstellung der Laurentreihe durch 2 holomorphe Funktionen

Seien $g:G\rightarrow \mathbb {C}$ und $h:G\rightarrow \mathbb {C}$ zwei holomorphe Funktionen mit Entwicklungspunkt $z_{0}\in G$

f(z):=g(z-z_{o})+{\hat {h}}(z-z_{o})

mit

{\hat {h}}(z):=h(1/z)

$g$ und $h$ sind holomorphe Funktionen auf $G_{o}:=\{z-z_{o}\in \mathbb {C} \ |\ z\in G\}$ , die sich um 0 in eine Potenzreihe in $G_{o}$ entwickeln lassen.

Konvergenzmenge der Laurentreihe

Die Funktionen $g$ und $h$ lassen sich lokal als Potenzreihe auf einer Kreisscheibe in $G_{o}:=\{z-z_{o}\in \mathbb {C} \ |\ z\in G\}$ darstellen (Holomorphiekriterium). Dann konvergiert ${\hat {h}}$ mit ${\hat {h}}(z):=h(1/z)$ auf dem Komplement einer Kreisschreibe.

Schnittmenge von Konvergenzbereichen

Wenn bei $f(z)$ der Hauptteil $g(z)$ und der ${\hat {h}}(z)$ konvergent sein $z$ im Schnitt der Konvergenzmenge liegen. Ist $r>R$ ist die Konvergenzmenge leer, da $z$ zugleich auf einer Kreisscheibe von Radius $R$ und im Komplement der Kreisscheibe mit Radius $r$ liegen muss.

Konvergenzradien

Seien $R_{g}>0$ und $R_{h}>0$ die Konvergenzradien für die Funktionen $g$ und $h$ . Berechen Sie den Radius $R_{\hat {h}}>0$ der Konvergenzmenge von ${\hat {h}}(z):=h(1/z)$ für den alle $z\in G_{o}$ mit $|z|>R_{\hat {h}}>0$ konvergieren.

Geometrie der Konvergenzmenge

$h$ ist um den Mittelpunkt holomorph konvergent auf der Kreisscheiben mit dem Radius $1/r$ . Da das Argument der Funktion $h$ innerhalb des so definierten Kreisgebietes liegen muss, erkennt man schnell, dass die Funktion $h(1/z)$ für Werte $|z|>r$ definiert ist. Damit ist auch die Summe der beiden Funktionen

f(z)=g(z)+h\left({\frac {1}{z}}\right)

auf dem Kreisring ${\mathcal {R}}$ analytisch.

Eindeutigkeit der Zerlegung

Es lässt sich zeigen, dass sich jede auf einem Ringgebiet holomorphe Funktion auf diese Weise zerlegen lässt. Setzt man dazu noch $h(0)=0$ voraus, so ist die Zerlegung eindeutig.

Entwickelt man diese Funktion nun in Form von Potenzreihen so ergibt sich folgende Darstellung:

f(z)=g(z)+h\left({\frac {1}{z}}\right)=\sum _{n=0}^{\infty }a_{n}z^{n}+\sum _{n=1}^{\infty }b_{n}z^{-n}=\sum _{n=-\infty }^{\infty }a_{n}z^{n}

.

Dabei wurde $b_{n}\equiv a_{-n}$ definiert. Außerdem folgt $b_{0}=0$ aus der Bedingung $h(0)=0$ .

Zerlegung mit Entwicklungspunkt

Erweitert man diese Überlegungen nun auf die Entwicklung um einen Punkt $c$ , und nicht so wie eben um den Ursprung, so ergibt sich die eingangs angeführte Definition der Laurent-Reihe für eine holomorphe Funktion $f$ um den Entwicklungspunkt $c$ :

f(z)=\sum _{n=-\infty }^{\infty }a_{n}(z-c)^{n}

Beispiel

Im Folgenden bezeichnet ${\textstyle \mathbb {K} }$ wahlweise die reellen oder komplexen Zahlen.

f\colon \mathbb {K} \to \mathbb {K} \colon x\mapsto {\begin{cases}\exp \left(-{\frac {1}{x^{2}}}\right),&x\neq 0\\0,&{\text{sonst}}\end{cases}}

.

Die Funktion ist unendlich oft reell differenzierbar, sie ist jedoch an der Stelle $x=0$ nicht komplex differenzierbar und hat dort sogar eine wesentliche Singularität.

Einsetzen in Taylorreihe

Indem man nun ${\textstyle z=-{\frac {1}{x^{2}}}}$ in die Potenzreihenentwicklung der Exponentialfunktion einsetzt,

exp(z)=\sum _{n=0}^{\infty }{\frac {z^{n}}{n!}}=\sum _{n=0}^{\infty }{\frac {\left(-{\frac {1}{x^{2}}}\right)^{n}}{n!}}

erhält man die Laurent-Reihe von ${\textstyle f}$ mit Entwicklungspunkt ${\textstyle 0}$ :

f(x)=\sum _{n=0}^{\infty }(-1)^{n}{\frac {x^{-2n}}{n!}}=\underbrace {\sum _{n=-\infty }^{-1}{\frac {(-1)^{n}}{(-n)!}}x^{2n}} _{\mbox{Hauptteil}}+1

Konvergenzbereich Laurentreihe

Der Nebenteil $g(x)=1$ konvergiert auf ganz $\mathbb {C}$ und der Hauptteil (und damit auch die Laurent-Reihe insgesamt) konvergiert für jede komplexe Zahl ${\textstyle x\neq 0}$ .

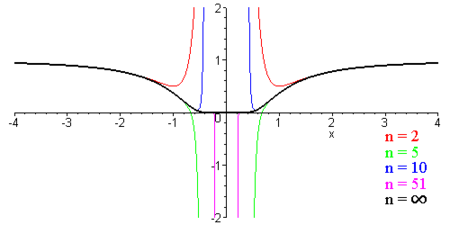
Approximation der Funktion durch Partial-Summen

Das Bild zeigt, wie sich die Partialsummenfolge

f_{n}(x)=\sum _{j=0}^{n}(-1)^{j}{\frac {x^{-2j}}{j!}}

an die Funktion annähert.

Graphen der Partial-Summen im Vergleich zur Funktion

.

Da Graphen in $\mathbb {C}$ Teilmengen von 4-dimensionalen $\mathbb {R}$ -Vektoräumen sind, wird hier der Graph für Werte aus $x\in \mathbb {R} \setminus \{0\}$ geplottet. Die Laurententwicklung lässt sich in 0 stetig fortsetzen.

Konvergenz von Laurent-Reihen

Laurent-Reihen sind wichtige Hilfsmittel der Funktionentheorie, vor allem zur Untersuchung von Funktionen mit isolierten Singularitäten.

Kreisringe und Kreisscheibe

Laurent-Reihen beschreiben komplexe Funktionen, die auf einem Kreisring holomorph sind, so wie Potenzreihen Funktionen beschreiben, die auf einer Kreisscheibe holomorph sind.

Sei

\sum _{n=-\infty }^{\infty }a_{n}(z-c)^{n}

eine Laurent-Reihe in $z$ mit komplexen Koeffizienten $a_{n}$ und Entwicklungspunkt $c$ .

Konvergenzradien - Inneres vom Kreisring

Es gibt es zwei eindeutig bestimmte Zahlen $r$ und $R$ , so dass Folgendes gilt:

Die Laurent-Reihe konvergiert auf dem offenen Kreisring

A:=\{z:r<\vert z-c\vert <R\}

normal, also insbesondere absolut und lokal gleichmäßig. Damit meint man, dass Haupt- und Nebenteil normal konvergieren. Lokal gleichmäßige Konvergenz impliziert gleichmäßige Konvergenz auf jeder kompakten Teilmenge von

A

, also insbesondere auf den Bildern von Kurven in

A

. Die Laurent-Reihe definiert auf

A

eine holomorphe Funktion

f

.

Außerhalb vom Kreisring

Außerhalb des Kreisrings divergiert die Laurent-Reihe. Das heißt, dass für jeden Punkt im Äußeren von $A$ mit

\mathbb {C} \setminus {\overline {A}}:=\{z:r>\vert z-c\vert \vee \vert z-c\vert >R\}

,

die Reihe der Terme mit positiven (Nebenteil) oder die Terme mit negativen Exponenten (Hauptteil) divergiert.

Rand von Kreisringen

Auf dem Rand des Kreisrings kann man keine allgemeinen Aussagen machen, außer dass es mindestens einen Punkt auf der äußeren Begrenzung und mindestens einen Punkt auf der inneren Begrenzung gibt, in die $f$ nicht holomorph fortgesetzt werden kann.

Es ist möglich, dass $r=0$ und $R=\infty$ ist, es kann aber auch sein, dass $r=R$ ist.

Konvergenzradien und Cauchy-Hadamard

Die beiden Radien können wie folgt mit der Formel von Cauchy-Hadamard berechnet werden:

r=\limsup _{n\to \infty }\vert a_{-n}\vert ^{1/n}

R={\frac {1}{\limsup _{n\to \infty }\vert a_{n}\vert ^{1/n}}}

Man setzt ${\frac {1}{0}}=\infty$ und ${\frac {1}{\infty }}=0$ in der zweiten Formel.

Auf Kreisringen definierte Funktionen

Umgekehrt kann man mit einem Kreisring $A:=\{z:r<\vert z-c\vert <R\}$ und einer auf $A$ holomorphen Funktion $f$ beginnen. Dann existiert immer eine eindeutig bestimmte Laurent-Reihe mit Entwicklungspunkt $c$ , die (mindestens) auf $A$ konvergiert und dort mit $f$ übereinstimmt. Für die Koeffizienten gilt

a_{n}={\frac {1}{2\pi \mathrm {i} }}\oint _{\partial U_{\varrho }(c)}{\frac {f(\zeta )}{\left(\zeta -c\right)^{n+1}}}\mathrm {d} \zeta

für alle $n\in \mathbb {Z}$ und ein $\varrho \in (r,R)$ . Wegen des Integralsatzes von Cauchy kommt es auf die Auswahl von $\varrho$ nicht an.

Gelochte Kreisscheibe

Der Fall $r=0$ , also der einer holomorphen Funktion $f$ auf einer gelochten Kreisscheibe um $c$ , ist besonders wichtig. Der Koeffizient $a_{-1}$ der Laurentreihenentwicklung von $f$ heißt Residuum von $f$ in der isolierten Singularität $c$ , er spielt eine große Rolle im Residuensatz.

Formale Laurent-Reihen

Formale Laurent-Reihen sind Laurent-Reihen in der Unbestimmten ${\textstyle X}$ , die ohne Rücksicht auf Konvergenzbetrachtungen benutzt werden.

Laurent-Reihen auf kommutativen Ringen

Die Koeffizienten ${\textstyle a_{k}}$ können dann aus einem beliebigen kommutativen Ring stammen. In dieser Situation ist es jedoch nur sinnvoll, Laurent-Reihen mit nur endlich vielen negativen Exponenten zu betrachten, also mit einem so genannten endlichen Hauptteil, und die Entwicklungsstelle mit ${\textstyle c=0}$ wegzulassen.

Gleichheit von formalen Laurent-Reihen

Zwei solche formale Laurent-Reihen sind per Definition genau dann gleich, wenn sie in allen Koeffizienten übereinstimmen. Zwei Laurent-Reihen werden addiert, indem ihre entsprechenden Koeffizienten addiert werden und weil sie nur endlich viele Terme mit negativem Exponenten haben, können sie durch Faltung ihrer Koeffizientenfolgen multipliziert werden, so wie es mit Potenzreihen gemacht wird. Mit diesen Verknüpfungen wird die Menge aller Laurent-Reihen über einem kommutativen Ring ${\textstyle R}$ zu einem kommutativen Ring, der mit ${\textstyle R\left(\!\left(X\right)\!\right)}$ bezeichnet wird.

Laurent-Reihen und Itegritätsringe

Ist $K$ ein Körper, dann bilden die formalen Potenzreihen in der Unbestimmten ${\textstyle X}$ über ${\textstyle K}$ einen Integritätsring, der mit $K\left[\!\left[X\right]\!\right]$ bezeichnet wird. Sein Quotientenkörper ist isomorph zum Körper ${\textstyle K\left(\!\left(X\right)\!\right)}$ der Laurent-Reihen über ${\textstyle K}$ .

Aufgaben

Sei $K_{r_{1},r_{2}}:=\{z\in \mathbb {C} \,|\,r_{1}<|z|<r_{2}\}$ . Konstruieren Sie eine Laurent-Reihe, die diesen Kreisring als Konvergenzbereich hat und auf $\mathbb {C} \setminus {\overline {K_{r_{1},r_{2}}}}$ nicht konvergiert. Verwenden Sie dabei als Idee geometrische Reihen mit $\sum _{n=0}^{+\infty }q^{n}$ konvergiert für $q\in \mathbb {C}$ für $|q|<1$ .

Aufgaben zu Laurent-Reihen und b-adischen Zahlsystemen

Analysieren Sie den Zusammenhang zwischen Laurent-Reihen und dem p-adischen Zahlensystem (z.B. Dualsysstem, Hexaldezimalsystem)! Welche Gemeinsamkeiten und welche Unterschiede gibt es?
Stellen Sie die Zahl ${\frac {1}{7}}$ als Funktionswert einer Laurent-Reihe im 4er-Zahlensystem $x=4$ dar, wobei $c_{n}\in \{0,1,2,3\}$ gilt und berechnen Sie die Koeffizienten $c_{n}$ !

f(x):=\sum _{n=-\infty }^{+\infty }c_{n}\cdot z^{n}

dar

Literatur

Eberhard Freitag & Rolf Busam: Funktionentheorie 1, Springer-Verlag, Berlin, ISBN 3-540-67641-4

Siehe auch

Seiteninformation

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Funktionentheorie' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Laurent-Reihe
siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.