Projekt:Mathematik ist überall/Fraktale

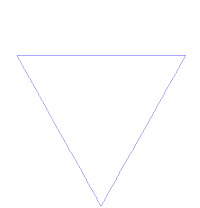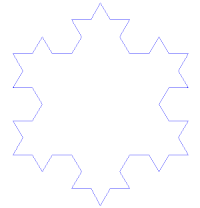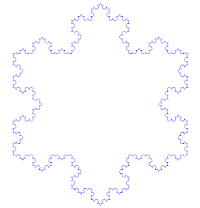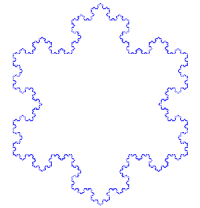Der Begriff „Selbstähnlichkeit“ ist sprachlich eher als Fehlgriff zu bewerten. Eigentlich resultiert er aus dem Bemühen der Mathematik, die Essenz des Forschungsgebiets einfach auszudrücken. Wenn allerdings ein „Selbst“ sich nicht mindestens ähnlich ist, dann hat das „Selbst“ ein Problem.

Grob gesehen handelt es sich bei „selbstähnlichen“ Gebilden um Fraktale. Das sind Objekte, deren Geometrie nicht – oder nicht ausreichend – mit herkömmlichen Mitteln zu beschreiben ist. Die Mathematik benutzt dann gern gebrochene Dimensionen (engl: fractal dimensions), um eine bessere mathematische Beschreibung zu ermöglichen.

Ein Beispiel ist die Kochsche Schneeflocke. Die Entwicklung dieser Figur führt nach unendlich vielen Schritten zwar zu einer begrenzten Fläche, aber ihr Umfang ist dann unendlich.

Gebrochene Dimensionen

Die Mathematik findet „Gebrochenes“ offensichtlich interessant. So hat sie einer ihrer alten Grundlagen, den Zahlen, die solide Basis entzogen und „gebrochene Basen“ eingeführt – und jetzt will sie auch noch die Geometrie ihrer Dimensionen berauben.

Im Jahre 1967 stellte der französische Mathematiker Benoît Mandelbrot genau diese Frage. Die Antwort bescherte der Mathematik gleich zwei neues Gebiete. Die Chaostheorie und die Fraktale.

Damit ist auch ein direkter Bezug mit der Kochschen Schneeflocke gegeben, denn wird ihr Umfang mit immer mehr „Zacken“ versehen, wird er immer länger. So ist es nur eine Frage, wie detailliert Küsten- oder andere Begrenzungslinien vermessen werden.

Schnell wurden auch andere Bereiche unter diesen neuen Gesichtspunkten untersucht. Selbst Blutgefäße, Nervengeflechte (Hirn), Baumkronen usw. verlangten nach neuen Möglichkeiten der „Vermessung“.

Zu diesem Gebiet der Mathematik ist sehr viel anschauliches Material verfügbar. Eine der ergiebigsten Fundgruben ist dabei die Universität Bremen.

Begrenzt aber Unendlich

Die erste Reaktion auf diese Überschrift besteht oft in der Aussage: „Das ist ein Widerspruch“. Nun, hier geht es um Mathematik. Daher ist also äußerste Vorsicht geboten, wenn das Wort „Widerspruch“ benutzt wird. Eine andere Variante der diesen Abschnitt überschreibenden Aussage lautet:

„Unendlich, aber nicht grenzenlos.“

Und tatsächlich: Es ist kein Widerspruch. Es sind solche Objekte, wie die Kochsche Schneeflocke, die derartige Eigenschaften besitzen.

Sie sind deshalb so interessant, weil der Beweis dieser Eigenschaft so einfach ist. Jede Seite hat den gleichen Aufbau und damit die gleiche Entwicklung.

Dieser Vorgang wiederholt sich in jeder weiteren Generation an jedem geraden Teilstück des Umfangs. Der Beweis ist nun sehr einfach. Der Umfang wird bestimmt durch die Addition aller Seitenlängen. Bei jedem Schritt verlängert sich jede Seite um den Faktor ${\frac {4}{3}}\$ . Wenn mit $U_{0}\$ der Anfangszustand (gleichseitiges Dreieck) der Schneeflocke bezeichnet wird und jede Seite die Länge 1 hat, dann gilt: $U_{0}=3\,;\ U_{1}=3\cdot {\frac {4}{3}}=4\,;\ U_{2}=3\cdot \left({\frac {4}{3}}\right)^{2}={\frac {48}{9}}\,;...$

Dann ergibt sich für den n-ten Schritt und den anschließenden Grenzübergang

$U_{n}=3\cdot \left({\frac {4}{3}}\right)^{n}\,;\ U=\lim _{n\to \infty }3\cdot \left({\frac {4}{3}}\right)^{n}=\infty \qquad q.e.d.$

Fraktale haben offensichtlich Eigenschaften, die von normalen Objekten sehr unterschiedlich sind. Dieses Gebiet der Mathematik ist noch sehr jung und die Auswirkungen auf andere Wissenschaften sind kaum abzusehen. Die folgenden Abschnitte werden „Selbstähnlichkeit“ in Bereichen zeigen, die kaum noch Gegenstand eingehender Untersuchungen sind, weil sie so einfach erscheinen. Vorher müssen sind aber kurz einige Überlegungen und Gegebenheiten angesprochen werden.

Die Mutter aller Fraktale

So etwas wie das „Urfraktal“ gibt es nicht! Aber das gleichseitige Dreieck ist derart oft anzutreffen, dass es sich für die weiteren Betrachtungen wie keine anderes Objekt anbietet.

Bereits die ältesten überlieferten „Anordnungen“ von Zahlen unterlagen der Form eines Dreiecks. So zeigte bereits im Jahre 1303 der chinesische Mathematiker Zhu Shijie das heute nach Blaise Pascal benannte Dreieck.

Diese Zahlenanordnung ist seit Jahrhunderten bekannt und liefert immer wieder Überraschendes. Ein Grund für das häufige Auftreten des gleichseitigen Dreiecks in diesem Zusammenhang könnte tatsächlich im Pascalschen Dreieck selbst liegen. Die angeordneten Zahlen sind Tetraederzahlen. Das Dreieck ist nur ein zweidimensionaler Tetraeder. So betrachtet ist das Dreieck dem (Pascalschen) Dreieck entnommen. Wie die Abbildung zeigt, sind im Pascalschen Dreieck gleich alle Dimensionen für Tetraeder enthalten. Damit entsprechen also die „1“-Zellen „null-dimensionalen“ Tetraedern.

Geometrie oder Muster?

Die Zahlen im Pascalschen Dreieck nehmen sehr schnell große Werte an. Das macht es schwierig, nach gemeinsamen Eigenschaften zu suchen. Glücklicherweise gibt es mittlerweile Computer, denen diese Aufgabe übergeben werden kann.

Eine Eigenschaft von natürlichen Zahlen ist die Parität , also die Feststellung, ob eine Zahl gerade oder ungerade ist. Bekannt ist, dass diese Eigenschaft von Zahl zu Zahl wechselt.

Dreiecke in Dreiecken

Die nebenstehende Abbildung zeigt die Tetraederzahlen (Binomialkoeffizienten) als „Minidreieck“, wenn die Eigenschaft ungerade vorhanden ist.

Hier zeigt sich ein selbstähnliches Muster. Es sind jetzt Dreiecke, die alternieren. Sie haben ihre Grundseite mal unten und mal oben. Gleichzeitig sind sie ihrerseits wieder aus Dreiecken aufgebaut. Es ist tatsächlich ein „fraktales“ Muster.

Tetraeder sind jedoch nicht zu erkennen, oder? Vielleicht nicht in der Höhe (die fehlt), dafür aber als geometrisches Gitter. Mit etwas gutem Willen sind vier Dreiecke zu erkennen: Ein helles, umgeben von drei dunkleren. Werden die drei dunklen „hochgeklappt“ ist ein Tetraeder vorhanden. Dabei ergibt sich für jede Seitenfläche des Tetraeders wieder ein entsprechendes Gitter. Der Tetraeder kann also in immer kleinere Tetraeder „zusammengeklappt“ werden.

In der nebenstehenden Abbildung sind die blauen Dreiecke also die Grundflächen der Tetraeder, welche aus den Seitenflächen „zusammengeklappt“ werden können. Es zeigt sich, dass auch die Tetraeder selbstähnlich sind. Werden die Seitenflächen nach innen (in Richtung des Körpermittelpunkts) „geklappt“, ergeben sich „Durchdringungen“ mehrerer Teraederspitzen. Diese „Körper“ entpuppen sich ihrerseits als die Projektionen der „höherdimensionalen“ Tetraeder auf die jeweils niedrigere Dimension.

Aus den Mustern, das die einzelnen „Punkte“ bilden, wird eine geometrische Figur einfach dadurch „erklärt“, dass zusammenhängende Punkte eine „Linie“ bilden. Die für Strecken erforderlichen Punkte ergeben sich dann einfach durch den Ort, an dem kein „Linienpunkt“ mehr vorhanden ist. So gelingt es, aus einem Muster eine geometrische Figur zu „erklären“.

Selbstähnlicher Zufall

Können zufällige Ereignisse selbstähnlich sein? Nein, aber ihre Abfolge. Genauer gesagt, das Muster von Orten, die mit einem zufälligen Ereignis assoziiert werden. Hört sich kompliziert an, ist aber ganz einfach. Es genügt ein Würfel, ein gezeichnetes Dreieck, Lineal und Bleistift.

Der Ablauf

Einen beliebigen Ausgangspunkt $p_{0}\$ wählen.
Würfeln, und bei mehr als 3 Augen einfach 3 abziehen.
Das Lineal vom Punkt $p_{0}\$ zur Ecke mit erwürfelter Zahl anlegen.
Genau auf der halben Strecke den neuen $p_{1}\$ markieren.
Dieser Punkt ist der neue Ausgangspunkt und der ganze Vorgang wird wiederholt.

Nachsehr vielen Wiederholungen ergibt sich ein Muster, ähnlich dem hier gezeigten.

Wie kann das sein? Der Zufall kennt keine Muster. Es liegt an der „Adressierung“ der Dreiecke. Sie erfolgt indirekt über die Cantor-Menge. Eine genaue Besprechung würde den hier gesteckten Rahmen sprengen. Hier wird nur auf die Arbeiten von Peitgen, Jürgens, Saupe und Barnsley verwiesen.

Selbstähnliche Logik

Logik hat etwas mit „wahr“ und „falsch“ zu tun. Wie soll hier etwas ähnlich sein und zu was ähnlich? Im Abschnitt „Logisch! Oder?!“ wurde von der Berechenbarkeit der Logik gesprochen und auf den Kurs zu Syllogismen verwiesen. Die dort besprochenen Gegebenheiten werden hier benutzt, um die „Selbstähnlichkeit“ der Logik zu zeigen.

Logik ist berechenbar; diese Tatsache ist bereits ein Selbstbezug. Die gängigen Computer arbeiten mit dem Dualsystem. Mit sog. logischen Schaltkreise werden die Berechnungen auf Basis der Logik ausgeführt. Wenn also die Schaltkreise mit Logik rechnen und die Logik berechenbar ist, dann kann die Logik mit Logik berechnet werden.

Derartige Bezüge auf sich selbst sind ein Indiz für Selbstähnlichkeit. Um den Nachweis zu führen, muss ganz unten angefangen werden. Die Mathematik meint sowas wörtlich. Es muss bei Operationen für eine logischen Aussage („wahr“, „nicht wahr“) und den möglichen Ergebnissen aller Operationen begonnen werden. Alle Operationen?! Wie viele gibt es denn überhaupt?

Wieviele logische Operationen?

	Aussage (bzw. $x\$ )	Ergebnis (bzw. $y\$ )
1. Nichts oder „NA_UND?“-Gatter	„wahr“	„wahr“
1. Nichts oder „NA_UND?“-Gatter	„falsch“	„falsch“

2. Dagegen oder „NEGATIONS“-Gatter	„wahr“	„falsch“
2. Dagegen oder „NEGATIONS“-Gatter	„falsch“	„wahr“

3.Trotzdem oder „IMMER“-Gatter	„wahr“	„wahr“
3.Trotzdem oder „IMMER“-Gatter	„falsch“	„wahr“

4. Ablehnen oder „NIEMALS“-Gatter	„wahr“	„falsch“
4. Ablehnen oder „NIEMALS“-Gatter	„falsch“	„falsch“

Also ich kann mir sehr viele Operationen vorstellen. Wirklich? Mathematik hilft sogar bei „überbordender Phantasie“. Vorstellungskraft ist gut, Nachweis der Existenz ist besser. Die Schaltkreise – ab jetzt „Gatter“ genannt – werden jetzt über die zur Verfügung stehenden Möglichkeiten hergeleitet und mit Namen (nicht den richtigen) versehen.

Was kann mit „wahr“ oder „falsch“ unternommen werden um ein Egebnis zu erhalten? Erst einmal muss das Ergebnis entweder „wahr“ oder „falsch“ sein, denn sonst würde der Wertebereich der Logik verlassen werden. Nachdem das geklärt ist; was kann mit einer logischen Aussage angestellt werden?

Nun, mehr Operationen als die nebenstehenden für eine logische Aussage existieren nicht. Wenn jetzt noch „wahr“ mit 1 und „falsch“ mit 0 bewertet wird und die „Aussage“ mit $x\$ und das „Ergebnis“ mit $y\$ bezeichnet wird, kann die Rechnerei losgehen.

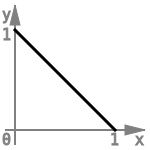
Von den vier Operationen dürfte die Negation am bekanntesten sein. Sie wird einfach als lineare Funktion angesehen, mit dem Graphen:

Die Funktion hat die allgemeine Form $y=f(x)=m\cdot x+b\$ . Diese Form ist bekannt. Es erleichtert die ganze Sache, wenn wir statt m und b hier andere Bezeichner verwenden:

$y=f(x)=a_{0}+a_{1}\cdot x\$
Aus der Wahrheitstabelle werden die Werte für x und y entnommen.

x	y
0	1
1	0

Nun müssen nur noch die as bestimmt werden. Es sind zwei Unbekannte, aber auch zwei Gleichungen; eine für x=0 und eine x=1 mit bekanntem y. In den allgemeinen Gleichungen sind die Zeilenummern der Wahrheitstabelle an den Variablen x und y als „geklammerte Exponenten“ vorhanden.

${\begin{aligned}a_{0}+a_{1}\cdot x^{\left(1\right)}=y^{\left(1\right)}\;;\ a_{0}+a_{1}\cdot {0}={1}\\a_{0}+a_{1}\cdot x^{\left(2\right)}=y^{\left(2\right)}\;;\ a_{0}+a_{1}\cdot {1}={0}\\\end{aligned}}$

Die Unbekannten sind mit $a_{0}=1\$ und $a_{1}=-1\$ schnell bestimmt. Für die Gleichung der Negation ergibt sich:

$y=f(x)=1+(-1)\cdot x=1-x\$

Alle auf einmal

Die eben gezeigte Vorgehensweise ist für Mathematiker nicht zu akzeptieren. Sie werden sofort an die lineare Algebra erinnert, denn das ist es, was sie in den ersten Semestern lernten. Für Mathematiker ist dieses Teilgebiet der Mathematik ungefähr so wichtig, wie ein Computer für Informatiker.

Deshalb wird das Gleichungssystem auch anders gesehen. Für Mathematiker steht statt der beiden Gleichungen einfach

${\begin{pmatrix}1&0\\1&1\end{pmatrix}}\cdot {\begin{pmatrix}a_{0}\\a_{1}\end{pmatrix}}={\begin{pmatrix}y^{\left(0\right)}\\y^{\left(1\right)}\end{pmatrix}}$

Damit lassen sich auch alle anderen Operationen ermitteln. Mit Matrizen und Vektoren lässt sich ähnlich einfach umgehen, wie mit normalen Zahlen. Es können nun alle vier Operationen in einer Gleichung geschrieben werden, um die entsprechenden $a_{s}\$ zu finden.

${\begin{pmatrix}a_{0}\\a_{1}\end{pmatrix}}={\begin{pmatrix}y^{\left(1\right)}\\y^{\left(2\right)}\end{pmatrix}}\cdot {\begin{pmatrix}1&0\\1&1\end{pmatrix}}^{-1}={\begin{pmatrix}y^{\left(1\right)}\\y^{\left(2\right)}\end{pmatrix}}\cdot {\begin{pmatrix}1&0\\-1&1\end{pmatrix}}$

Damit ergeben sich die einzelnen Komponenten des Vektors aus

$a_{0}=y^{\left(1\right)}\$

$a_{1}=-y^{\left(1\right)}+y^{\left(2\right)}\$

Der Exponent „-1“ bei der Matrix bedeutet einfach „invertierte Matrix“. Sie ist wichtig für die weiteren Betrachtungen und es ist normalerweise recht schwierig sie zu ermitteln. Hier aber nicht. Mathematik liebt es kurz und bündig. Die Matrix erhält den Namen

$\Psi ^{\left(1\right)}={\begin{pmatrix}1&0\\1&1\end{pmatrix}}$

Die hochgestellte „(1)“ bezeichnet die Anzahl der Aussagen (x-Variablen), die von den Operationen betroffen sind. Die allgemeine Schreibweise ist nun

${\vec {a}}={\vec {y}}\cdot \left(\Psi ^{\left(1\right)}\right)^{-1}$

Mehr Aussagen

Die bisherigen Operationen waren auf eine Aussage beschränkt. Umfangreicher wird es bei mehreren Aussagen. Es sind jetzt Verknüpfungen wie „ODER“, „UND“, sowie Relationen wie „gleich“, „ungleich“ zu berücksichtigen. Für den Anfang genügen zwei Aussagen. Wieder wird mit Tabelle und Gleichung(en) begonnen.

$x_{2}\$	$x_{1}\$	$y\$
$0\$	$0\$	$y^{\left(1\right)}\$
$0\$	$1\$	$y^{\left(2\right)}\$
$1\$	$0\$	$y^{\left(3\right)}\$
$1\$	$1\$	$y^{\left(4\right)}\$

Die Gleichung lautet:

$y=a_{0}+a_{1}\cdot x_{1}+a_{2}\cdot x_{2}+a_{12}\cdot x_{1}\cdot x_{2}$

Die Matrix für das Gleichungssystem ist jetzt

$\Psi ^{\left(2\right)}={\begin{pmatrix}1&0&0&0\\1&1&0&0\\1&0&1&0\\1&1&1&1\end{pmatrix}}$

Wieder bezeichnet das hochgestellte „(2)“ die Anzahl der Variablen. Die invertierte Matrix ist auch jetzt erforderlich, um die allgemeine Schreibweise verwenden zu können. Diese Matrix wird hier einfach mal so gezeigt.

$\left(\Psi ^{\left(2\right)}\right)^{-1}={\begin{pmatrix}1&0&0&0\\-1&1&0&0\\-1&0&1&0\\1&-1&-1&1\end{pmatrix}}$

Die Ähnlichkeiten zu den „kleinen“ Matrizen sind unübersehbar – würden Mathematiker mit einem Hang zur linearen Algebra feststellen. Weil dieser „Hang“ aber nicht so weit verbreitet ist, im nächsten Abschnitt die einfache Erklärung.

Selbsterzeugung

Die beiden großen Matrizen erzeugen sich selbst aus den kleinen. Es sind die letzten umfangreichen Formeln. Sie sind nur vorhanden, um die Voraussetzungen zu zeigen. Es geht nämlich auch viel einfacher, aber der mathematische Hintergrund wäre nicht mehr zu erkennen.

$\Psi ^{\left(2\right)}={\begin{pmatrix}1&0&0&0\\1&1&0&0\\1&0&1&0\\1&1&1&1\end{pmatrix}}={\begin{pmatrix}{\boldsymbol {1}}\cdot {\begin{pmatrix}1&0\\1&1\end{pmatrix}}&{\boldsymbol {0}}\cdot {\begin{pmatrix}1&0\\1&1\end{pmatrix}}\\\\{\boldsymbol {1}}\cdot {\begin{pmatrix}1&0\\1&1\end{pmatrix}}&{\boldsymbol {1}}\cdot {\begin{pmatrix}1&0\\1&1\end{pmatrix}}\end{pmatrix}}$

$\left(\Psi ^{\left(2\right)}\right)^{-1}={\begin{pmatrix}1&0&0&0\\-1&1&0&0\\-1&0&1&0\\1&-1&-1&1\end{pmatrix}}={\begin{pmatrix}{\boldsymbol {1}}\cdot {\begin{pmatrix}1&0\\-1&1\end{pmatrix}}&{\boldsymbol {0}}\cdot {\begin{pmatrix}1&0\\-1&1\end{pmatrix}}\\\\{\boldsymbol {-1}}\cdot {\begin{pmatrix}1&0\\-1&1\end{pmatrix}}&{\boldsymbol {1}}\cdot {\begin{pmatrix}1&0\\-1&1\end{pmatrix}}\end{pmatrix}}$

Dieser „Selbstaufbau“ sieht komplizierter aus als er ist. Die Klammern machen die Angelegenheit etwas übersichtlicher. Die allgemeine Formulierung für noch mehr Variablen ist unter dem Beitrag Syllogismen zu sehen.

Zellulärer Automat

Selbsterzeugung ist ein Indiz für Selbstähnlichkeit. Sind beide Kriterien vorhanden, kann sehr oft eine Vereinfachung des Aufbaus gefunden werden. Tatsächlich kann die Matrix $\Psi ^{\left(g\right)}\$ für jede Generation g durch einen zellulären Automaten aufgebaut werden. Dieser Automat ist bereits aus dem Schulunterricht bekannt.

Die „Umwelt“ des Automaten besteht aus einer Matrix, deren erste Spalte und letzte Zeile mit 1 belegt ist. Alle anderen Elemente $\psi _{i,k}\$ sind 0 (Null). Das erste „Element“, welches betrachtet wird, ist in der Matrix (Umwelt) farblich gekennzeichnet. Sein „Zustand“ (0 oder 1) ist bestimmt durch die links und unten liegenden Nachbar-Elemente.

Wenn die Matrix n Zeilen und m Spalten hat, ist das erste Element $\psi _{(n-1),\;(m-1)}\$ . Die „Nachbarn“ sind die Elemente $\psi _{n,\;(m-1)}\$ (linker „Nachbar“) und $\psi _{(n-1),\;m}\$ (unterer „Nachbar“). Sind die „Nachbarn“ gleich, hat das Element den Zustand 0, sind sie ungleich, wird das Element zu 1.

Die „Bearbeitungsrichtung“ der vielleicht zu ändernden Elemente ist durch die farblichen Pfeile angegeben. Dabei wird zuerst die Zeile bis zum Ende bearbeitet. Ist die Zeile beendet, wird mit der darüber liegenden weitergemacht.

${\begin{bmatrix}1&0&\cdots &0\\1&\color {BurntOrange}{\boldsymbol {\uparrow }}&\ddots &0\\\vdots &\color {BurntOrange}{\boldsymbol {0}}&\color {BurntOrange}{\boldsymbol {\rightarrow }}&\vdots \\1&1&\cdots &1\end{bmatrix}}$

Das ist ein zellulärer Automat. Der Zustand eines Elements ist abhängig von der sog. Überführungsfunktion. Für eine Matrix mit n Zeilen und m Spalten lautet sie:

$\psi _{n,\;m}=\left(\psi _{(n+1),\;m}+\psi _{n,\;(m+1)}\right)\ mod\ 2\$

Es ergibt sich die gleiche Matrix, wie sie mit der vorher gezeigten Methode erzeugt wird. Aber noch etwas ist interessant, wird die „modulo 2“-Operation in der „Überführungsfunktion“ weggelassen, entsteht das bekannte Pascalsche Dreieck.

${\begin{pmatrix}{\boldsymbol {1}}&4&10&20\\{\boldsymbol {1}}&{\boldsymbol {3}}&6&10\\{\boldsymbol {1}}&2&{\boldsymbol {3}}&4\\{\boldsymbol {1}}&{\boldsymbol {1}}&{\boldsymbol {1}}&{\boldsymbol {1}}\end{pmatrix}}$

Es geht also noch viel einfacher. Die ungeraden Zahlen sind fett dargestellt und entsprechen damit einer 1 in der ursprünglichen Matrix. Mit dieser Übereinstimmung lassen sich viele Parallelen zur Zahlentheorie, Geometrie und sogar zur Topologie ziehen.

Erbliche Eigenschaften

Werden zwei Zahlen addiert, „erbt“ das Ergebnis (Summe) bestimmte Eigenschaften der Summanden. Diese „Vererbung“ ist bestimmten Regeln unterworfen. So kann durchaus von einer Art „Dominanz“ gesprochen werden. Die Eigenschaften der Summanden seien G für gerade und U für ungerade. Damit ergibt sich für die Summe:

$G+G=G\$

$G+U=U\$

$U+G=U\$

$U+U=G\$

Offensichtlich ist die Eigenschaft G immer dann vorhanden, wenn die Summanden gleich sind. Das G entspricht so einer 0 (Null) und U einer 1. Es genügt also, nur das kleinstwertige Bit der dual kodierten Summanden zu betrachten um die entsprechende Eigenschaft der Summe zu kennen. Das ist das Wesentliche der Addition, denn ein Addierer im Computer macht genau das Gleiche, allerdings für jedes Bit.

Vererbung graphischer Eigenschaften

Der Aufbau aus kleinen $2\times 2\$ Matrizen ist auch hier deutlich. Die Tetraederzahlen wurden bereits erwähnt und hier zeigt sich ein „fließender“ Übergang von der kleinsten Matrix zum Tetraeder(gitter). Dabei sind alle ungeraden Elemente blau und alle geraden rot gefärbt.

Das Teraedergitter ist ein Eulerscher Graph. Vom Startpunkt können alle Linien so gezogen werden, dass der Endpunkt wieder dem Startpunkt entspricht. Weil jedes der gleichseitigen Dreiecke durch Halbierung der Seiten wieder ein Teraedergitter ergibt, gilt die erwähnte Eigenschaft auch für jedes kleinere Gitter. Interessant ist nun, dass große Gitter, nun aus vier kleinen Gittern bestehend, ist wieder ein Eulerscher Graph. Die Eigenschaft wird also ebenfalls „vererbt“ und beibehalten. Weil gleichseitige Dreiecke auch als zweidimensionale Tetraeder angesehen werden können, gelten die Möglichkeiten der „Vererbung“ auch für höhere Dimensionen. Aus dem Sierpinski-Dreieck kann also auch ein Sierpinki-Tetraeder werden. Der Begriff „Tetrader“ erstreckt sich dann über alle Dimensionen.

Dadurch ist es möglich, eine rekursive Darstellung von beliebiger Tiefe zu erstellen. Ein interessantes Werkzeug zur Untersuchung ist mit dem „KTurtle“ vorhanden. Hier ein paar Beispiele mit unmittelbarem Bezug auf diesen Abschnitt.

Fraktales Atom

Es gibt eine untere Grenze für Fraktale dieses Typs. Irgendwann zerfällt die Struktur in Teile, von denen mindestens eines den anderen nicht ähnlich ist. Bei dem oben gezeigten Teraedergitter/Matrix ist genau das gegeben. Würden die Elementee dieser Figur(en) voneinander getrennt, hätten die einzelnen Objekte keinen Bezug mehr zu dem umgebenden Objekt das sie vorher gemeinsam bildeten. Es ist ein „fraktales“ Atom.

Selbstähnliche Prädikatenlogik

Das dauert noch bis zum Wochenende (Kalenderwoche???). Hier sollen die Erkenntnisse des bereits zitierten DNA-Modells mit rein.

Ich vermute einen neuen Projektmitarbeiter als Urheben?!

Erwähnenswertes

Die „Zerlegung“ der Seitenflächen des Tetraeders in der hier noch einmal gezeigten Art, bringt ein blaues „Objekt“ zutage.

Es handelt sich um die Kristallstruktur eines Diamanten. Präzise ist es die am häufigsten anzutreffende Kristallstruktur bei Diamanten. Wie eng Tetraeder und Oktaeder zusammenhängen wird in den „Notices of the AMS“, Ausgabe Februar 2008 von Prof. Sunada ausführlich dargelegt.