Kurs:Algebraische Kurven (Osnabrück 2008)/Vorlesung 8b

Beispiel (Kreis und Gerade durch Mittelpunkt II)

Wir gehen nun zum allgemeinen Fall über, wo der Koppelungsabstand $d$ nicht $1$ ist. Das mechanische System wird dann durch den Schnitt von zwei Zylindern mit unterschiedlichen Radien beschrieben. Aus den beiden Gleichungen kann man einfach $y_{2}$ eliminieren und erhält die Gleichung

x_{1}^{2} - 2 x_{1} x_{2} = (x_{2} - x_{1})^{2} - x_{2}^{2} = d^{2} - 1 .

Wir setzen $α = d^{2} - 1 = \neq 0$ und $w = x_{2} - x_{1}$ .

Für einen Punkt $P = P_{1} + u (P_{2} - P_{1})$ der Koppelungsstange sind die Koordinaten gleich

(z_{1}, z_{2}) = (x_{1} + u (x_{2} - x_{1}), u y_{2}) .

Wir wollen die Trajektorie zu diesem Punkt des mechanischen System berechnen. Bei $u = 0$ ist das einfach die Gerade, sodass wir im Folgenden $u \neq 0$ annehmen. Wir ersetzen

x_{2} = \frac{1}{u} (x_{1} (u - 1) + z_{1}) und y_{2} = \frac{1}{u} z_{2}

in der ersten und der eliminierten Gleichung und erhalten

${(\frac{x_{1} (u - 1) + z_{1}}{u})}^{2} + {(\frac{z_{2}}{u})}^{2} = 1$
$x_{1}^{2} - \frac{2}{u} x_{1} (x_{1} (u - 1) + z_{1}) = d^{2} - 1$

bzw.

$(u - 1)^{2} x_{1}^{2} + 2 (u - 1) z_{1} x_{1} + z_{1}^{2} + z_{2}^{2} - u^{2} = 0$
$(- u + 2) x_{1}^{2} - 2 z_{1} x_{1} - u d^{2} + u = 0 .$

Es liegen also zwei quadratische Gleichungen für $x_{1}$ über $K [z_{1}, z_{2}]$ vor. Mittels Fakt4.6 kann man daraus eine Gleichung für $z_{1}$ und $z_{2}$ errechnen, und zwar ergibt sich

{((- u + 2) (z_{1}^{2} + z_{2}^{2} - u^{2}) - (u - 1)^{2} (- u d^{2} + u))}^{2}

- 2 (u - 1) z_{1} [- (- u + 2) (z_{1}^{2} + z_{2}^{2} - u^{2}) (- 2 z_{1}) -

(- u d^{2} + u) (- u + 2) 2 (u - 1) z_{1} + (u - 1)^{2} (- 2 z_{1}) (- u d^{2} + u)]

+ (z_{1}^{2} + z_{2}^{2} - u^{2}) ((u - 1)^{2} (- 2 z_{1})^{2} - 2 (- u + 2) 2 (u - 1) z_{1} (- 2 z_{1})) = 0.

Das ist eine eben algebraische Kurve vom Grad vier, eine ziemlich hässliche Gleichung.

Beispiel (Zwei Kreise)

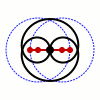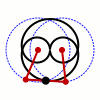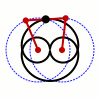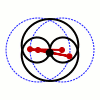
Als Bahnen betrachten wir jetzt zwei Kreise, wobei wir uns auf gleichen Radius beschränken, den wir zu $1$ normieren. Durch verschieben können wir annehmen, dass $(0, 0)$ und $(0, a)$ die Mittelpunkte der beiden Kreise sind. Die Länge der Koppelungsstange sei wieder $d$ , sodass die drei algebraischen Gleichungen

$(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2} = d^{2}$
$x_{1}^{2} + y_{1}^{2} = 1$
$(x_{2} - a)^{2} + y_{2}^{2} = 1$

das mechanische System beschreiben. Wir interessieren uns für die Trajektorie des Mittelpunktes der Stange. Dessen Koordinaten sind gegeben durch

z_{1} = \frac{1}{2} x_{1} + \frac{1}{2} y_{1} und z_{2} = \frac{1}{2} x_{2} + \frac{1}{2} y_{2} .

Wir drücken das System in den Variablen $z_{1}, z_{2}, x_{1}, x_{2}$ aus, ersetzen $y_{1} = 2 z_{1} - x_{1}, y_{2} = 2 z_{2} - x_{2}$ und erhalten

$(x_{2} - x_{1})^{2} + (2 z_{2} - 2 z_{1} - x_{2} + x_{1})^{2} = d^{2}$
$x_{1}^{2} + (2 z_{1} - x_{1})^{2} = 2 x_{1}^{2} + 4 z_{1}^{2} - 4 x_{1} z_{1} = 1$
$(x_{2} - a)^{2} + (2 z_{2} - x_{2})^{2} = 4 z_{2}^{2} - 4 x_{2} z_{2} + x^{2} + (x_{2} - a)^{2} = 1$ .

In der Gleichung (3) kommt $x_{1}$ nicht vor, und aus den Gleichungen (1) und (2) wollen wir $x_{1}$ eliminieren.

Wann sind für zwei gegebene algebraische Kurven $B_{1}$ und $B_{2}$ die Trajektorien des zugehörigen mechanischen Systems beschränkt? Dies ist nicht immer der Fall. So sind beispielsweise für zwei parallele Geraden die Trajektorien ebenfalls parallele Geraden (wenn der Stangenpunktabstand (Koppelungsabstand) mindestens so groß ist wie der Parallelabstand). Aber auch für kompliziertere Syteme gibt es unbeschränkte Trajektorien, wie das folgende Beispiel zeigt.

Beispiel

Die Zissoide des Diokles $C$ ist durch die Gleichung

Y^{2} (1 - X) = X^{3}

gegeben. Sie hat für reelles $x < 0$ keine reelle Lösung, da dann die rechte Seite negativ ist und keine Quadratwurzel besitzt. Sie hat auch für reelles $x \geq 1$ keine reelle Lösung, da dann die rechte Seite positiv, aber der Koeffizient $1 - x \leq 0$ ist, sodass es wieder keine reelle Lösung gibt. Für $x = 0$ ist $y = 0$ die einzige Lösung, und für $x$ , $0 < x < 1$ gibt es genau zwei Lösungen in $y$ , die beide reelle sind.

Wir betrachten nun die Zissoide zusammen mit der durch $x = 1$ definierten Geraden $G$ (im Bild grau) und das zugehörige mechanische Koppelungssystem mit Koppelungsabstand $d$ . Die Kurven $C$ und $G$ sind also die beiden Bahnen des mechanischen Stangensystems. Zu jeder reellen Zahlen $b \geq 0$ gibt es stets Punkte $Q_{1}, Q_{2}$ mit $Q_{1} \in C$ , $Q_{2} \in G$ , mit $d (Q_{1}, 0), d (Q_{2}, 0) \geq b$ und $d (Q_{1}, Q_{2}) = d$ . Daher gibt es unbeschränkte Trajektorien. Die Gerade selbst ist eine unbeschränkte (Koppelungspunkt-)Trajektorie für einen Koppelungsabstand $\geq 1$ ( $1$ ist nicht die exakte Grenze; für kleinen Koppelungsabstand ist ein beschränkter Ausschnitt um $(1, 0)$ nicht der Teil der Trajektorie) und die Zissoide ist eine (Koppelungspunkt-)Trajektorie, wenn der Koppelungsabstand $\geq 1$ ist (andernfalls ist ein beschränkter Teilbereich um den Nullpunkt nicht Teil der Trajektorie).

Definition

Zwei ebene, affine, reell-algebraische Kurven $B_{1}, B_{2} \subseteq ℝ^{2}$ heißen asymptotisch koppelungsfrei, wenn es zu jedem $d > 0$ ein $b > 0$ derart gibt, dass für alle Punkte $P_{1} \in B_{1}$ und $P_{2} \in B_{2}$ mit $P_{1}, P_{2} \in̸ B (0, b)$ gilt: $d (P_{1}, P_{2}) \geq 0$ .

Zwei Kurven sind insbesondere asymptotisch koppelungsfrei, wenn eine davon beschränkt ist. Aber auch zwei nicht parallele Geraden sind asymptotisch koppelungsfrei.

Lemma

Es seien $C_{1}, C_{2} \subset ℝ^{2}$ zwei ebene affine reell-algebraischen Kurven, die asymptotisch koppelungsfrei seien. Dann ist jede Trajektorie des zugehörigen mechanischen Koppelungssystems beschränkt.

Beweis

Es sei $d$ der Koppelungsabstand des zugehörigen mechanischen Systems und sei $P$ ein Punkt der bewegten Stange (oder Ebene), dessen Trajektorie wir untersuchen. Es sei $ϵ > 0$ das Maximum der Abstände von $P$ zu den beiden Koppelungspunkten. Zu $d$ gibt es aufgrund der Definition von asymptotisch koppelungsfrei ein $b > 0$ derart, dass es außerhalb der Ballumgebung kein Punktepaar gibt mit Abstand $d$ . Bei jeder erlaubten Konfiguration des mechanischen System muss also mindestens ein Koppelungspunkt innerhalb der Ballumgebung liegen, sagen wir ${P_{2}}^{'}$ . Dann gilt für den zugehörigen Bildpunkt $P^{'}$ von $P$ zu dieser Konfiguration die Abschätzung

d (P^{'}, 0) \leq d (P^{'}, {P_{1}}^{'}) + d ({P_{1}}^{'}, {P_{2}}^{'}) + d ({P_{2}}^{'}, 0) \leq ϵ + d + b .

D.h. also alle Trajektorienpunkte liegen in einer beschränkten Umgebung.

◻

<< | Kurs:Algebraische Kurven (Osnabrück 2008) | >>

PDF-Version dieser Vorlesung

Arbeitsblatt zur Vorlesung (PDF)