Kurs:Topologie (Osnabrück 2008-2009)/Vorlesung 1

Viele Begriffe der Topologie (wie Zusammenhang, kompakt, stetig) sind auch in anderen Gebieten der Mathematik wichtig.

Einige der Begriffe sind schon im Laufe einer Veranstaltung über Analysis reellwertiger Funktionen aufgetaucht. So sollte bereits klar sein, wann eine Abbildung $f\colon X\to Y$ zwischen Teilmengen $X\subseteq {\mathbb {R} }^{m},Y\subseteq {\mathbb {R} }^{n}$ eines euklidischen Raumes stetig ist. Hier sind wichtige Beispiele von solchen Teilmengen.

Definition (Topologische Äquivalenz von Teilmengen euklidischer Räume)

Eine stetige Abbildung ${}f\colon X\to Y$ zwischen Teilmengen ${}X\subseteq {\mathbb {R} }^{m},Y\subseteq {\mathbb {R} }^{n}$ ist eine topologische Äquivalenz, wenn es eine stetige Abbildung ${}g\colon Y\to X$ derart gibt, dass die Gleichungen ${}g\circ f=\mathrm {id} _{X}$ und ${}f\circ g=\mathrm {id} _{Y}$ gelten.

Definition (Die Sphäre)

Es sei ${}n\in \mathbb {N}$. Die ${}n$-Sphäre ist durch

${}S^{n}:={\left\{x=(x_{0},...,x_{n})\in \mathbb {R} ^{n+1}\mid x_{0}^{2}+x_{1}^{2}+\cdots +x_{n}^{2}=1\right\}}\subseteq \mathbb {R} ^{n+1}\,$

gegeben.

Definition (Der Würfel)

Es sei ${}n\in \mathbb {N}$. Der ${}n$-Würfel ist gegeben als das ${}n$-fache Produkt des Intervalls ${}[-1,1]$, also

$W^{n}\colon =[-1,1]\times [-1,1]\times ...\times [-1,1]\subseteq \mathbb {R} ^{n}.$

Eine andere Beschreibung ist

$W^{n}\colon =\lbrace x=(x_{1},...,x_{n})\in \mathbb {R} ^{n}:\vert x_{i}\vert \leq 1\,{\text{ für alle }}\,1\leq i\leq n\rbrace \subseteq \mathbb {R} ^{n}.$

Dessen Oberfläche oder Rand sei gegeben als

$\partial W^{n}\colon =\lbrace x=(x_{1},...,x_{n})\in W^{n}\,:\,\exists 1\leq i\leq n{\text{ mit }}\vert x_{i}\vert =1\rbrace \subseteq W^{n}.$

Beispiel (Topologische Äquivalenz von Teilmengen euklidischer Räume)

Der Kreis $S^{1}$ und das Quadrat $Q^{1}$ sind topologisch äquivalent. Eine topologische Äquivalenz ${}f\colon S^{1}\to Q^{1}$ ist gegeben durch

${}(x,y)\mapsto f(x,y)={\frac {1}{\max \lbrace \vert x\vert ,\vert y\vert \rbrace }}(x,y)\,\,$

und ${}f$ ist stetig als Komposition stetiger Abbildungen (Absolutbetrag, Maximum, Inverses, Skalarmultiplikation). Die Umkehrabbildung ${}g\colon Q^{1}\to S^{1}$ ist

${}(x,y)\mapsto g(x,y)={\frac {1}{\sqrt {x^{2}+y^{2}}}}(x,y)\,\,$

wie man nachrechnen kann. Die Abbildung ${}g$ ist wieder stetig als Komposition stetiger Abbildungen (Quadrat, Quadratwurzel, Summe, Inverses, Skalarmultiplikation).

Ebenso sind die Kugeloberfläche $S^{2}$ und die Würfeloberfläche $Q^{2}$ topologisch äquivalent. Aber die Kugeloberfläche $S^{2}$ und der Torus $S^{1}\times S^{1}$ sind nicht zueinander topologisch äquivalent. Es ist nicht leicht, für letzteres einen guten Grund (also einen Beweis) anzugeben, obwohl diese Tatsache ja recht plausibel erscheint.

Der Spezialfall ${}\mathbb {R} ^{n}$ ist schon instruktiv genug. Es ist ja aus der Linearen Algebra bekannt, dass es genau dann eine bijektive ${}\mathbb {R}$-lineare Abbildung

${}f\colon \mathbb {R} ^{m}\to \mathbb {R} ^{n}\,\,$

gibt, wenn ${}m=n$ gilt. Aber es gibt substantiell mehr stetige bijektive als lineare bijektive Abbildungen. Als ein Resultat in dieser Richtung sei die Peano-Kurve erwähnt.

Beispiel (Peano-Kurve)

Als Peano-Kurve bezeichnet man stetige surjektive Abbildungen ${}I\to I^{2}$ eines bestimmten Typs. Die erste Konstruktion stammt von Giuseppe Peano, und sie wurde damals als etwas Beunruhigendes empfunden. Zunächst sei angemerkt, dass eine stetige surjektive Abbildung $f\colon I\to I^{2}$ wiederum stetige und surjektive Abbildungen $f\times \operatorname {id} _{I^{n-1}}\colon I^{n}\to I^{n+1}$ liefert, und durch Verkettung erhält man eine stetige Surjektion $I\to I^{n}$ für jedes $n\in \mathbb {N}$. Des weiteren erlaubt eine stetige surjektive Abbildung ${}I\to I^{n}$ die Definition einer stetigen surjektiven Abbildung ${}\mathbb {R} \to \mathbb {R} ^{n}$, indem man ${}\mathbb {R} ^{n}$ auf geeignete Weise durch abzählbar viele Würfel ${}I^{n}$ überdeckt.

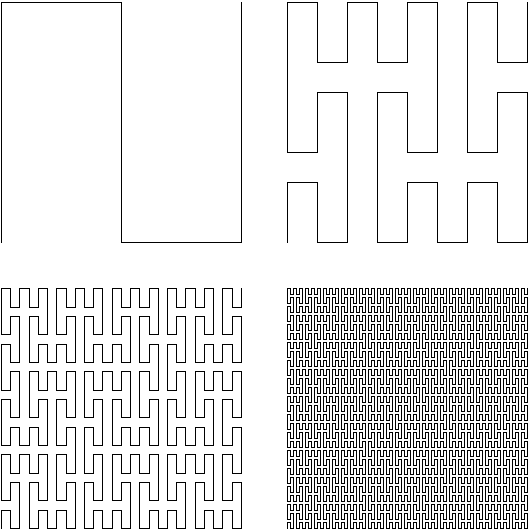
Zur Konstruktion einer Peano-Kurve gebe ich einige Bilder an, die andeuten, wie der Grenzwert einer geeigneten Folge stetiger (sogar stückweise linearer) Abbildungen ${}I\to I^{2}$ eine stetige surjektive Abbildung ${}I\to I^{2}$ liefert. Man beginnt mit der Unterteilung eines Quadrats in neun gleich große Quadrate, die in einer S-Kurve durchlaufen werden. Im nächsten Schritt wird jedes dieser Quadrate wieder unterteilt und die entstehenden Quadrate in S-Kurven durchlaufen, die als neue Kurve zusammengehängt werden:

Skaliert man die Kurven auf dieselbe Größe, erhält man folgendes Bild:

Nun werde ich eine präzise Definition einer surjektiven stetigen Abbildung ${}I\to I^{2}$ mit Hilfe der Cantor-Menge geben. Die informelle Beschreibung der Cantor-Menge lautet so:

Man beginnt mit dem abgeschlossenen Intervall $[0,1]$ der reellen Zahlen von 0 bis 1. Aus diesem Intervall wird das offene mittlere Drittel entfernt, also alle Zahlen, die strikt zwischen 1/3 und 2/3 liegen. Übrig bleiben die beiden Intervalle $[0,{\tfrac {1}{3}}]$ und $[{\tfrac {2}{3}},1]$. Aus diesen beiden Intervallen wird wiederum jeweils das offene mittlere Drittel entfernt und man erhält nun vier Intervalle: $[0,{\tfrac {1}{9}}]$, $[{\tfrac {2}{9}},{\tfrac {1}{3}}]$, $[{\tfrac {2}{3}},{\tfrac {7}{9}}]$ und $[{\tfrac {8}{9}},1]$. Von diesen Intervallen werden wiederum die offenen mittleren Drittel entfernt. Dieser Schritt wird unendlich oft wiederholt. Die Cantor-Menge besteht nun aus allen Punkten, die jedes Entfernen überlebt haben. Das Bildchen dazu sieht so aus:

Man kann die Cantor-Menge auch als die Menge aller reellen Zahlen $x\in I=[0,1]$ beschreiben, die eine Darstellung ${}\sum _{n=1}^{\infty }{\frac {a_{n}}{3^{n}}}$ als Kommazahl zur Basis 3 besitzen, in der nur die Ziffern 0 und 2 vorkommen. Insbesondere enthält die Cantor-Menge mehr als nur die Randpunkte der entfernten Intervalle; diese Randpunkte sind genau die Zahlen in $[0,1]$, welche sich mit einer 0-Periode oder mit einer 2-Periode schreiben lassen, zum Beispiel

$1/3=2\cdot 3^{-2}+2\cdot 3^{-3}+2\cdot 3^{-4}+\cdots =0{,}0{\overline {2}}_{3}=0{,}1_{3}$

Auch 1/4 liegt in der Cantor-Menge, denn

$1/4=2\cdot 3^{-2}+2\cdot 3^{-4}+2\cdot 3^{-6}+\cdots =0{,}{\overline {02}}_{3}$

Tatsächlich ist die triadische Darstellung einer Zahl in der Cantor-Menge eindeutig, wenn man fordert, dass die 1 nicht als Ziffer auftaucht.

Bezeichne nun ${}C$ die Cantor-Menge, dann gibt es eine surjektive stetige Abbildung ${}g\colon C\to I$. Sie ist definiert als

${}g{\Bigl (}\sum _{n=1}^{\infty }{\frac {a_{n}}{3^{n}}}{\Bigr )}\colon =\sum _{n=1}^{\infty }{\frac {\frac {a_{n}}{2}}{2^{n}}}\,\,$

In Worten: ${}g$ halbiert die Ziffern einer triadischen Darstellung und nimmt sie als Ziffern einer duadischen oder binären Darstellung. Da jede reelle Zahl eine duadische Darstellung besitzt, ist ${}g$ surjektiv. Es sei nun ${}\epsilon >0$ und ${}n\in \mathbb {NN}$ mit ${}{\frac {1}{2^{n}}}<\epsilon$, dann ist f\"ur zwei Punkte ${}x,y\in C$ mit ${}\vert x-y\vert <{\frac {1}{3^{n}}}$ schon

${}\vert g(x)-g(y)\vert \leq \sum _{i={n+1}}^{\infty }{\frac {1}{2^{i}}}={\frac {1}{2^{n}}}<\epsilon \,\,$

Denn die triadischen Darstellungen von ${}x,y$ unterscheiden sich nicht vor der ${}n+1$-ten Stelle. Also ist ${}g$ stetig.

Des weiteren gibt es eine surjektive Abbildung ${}h\colon C\to C\times C$, die durch

${}h{\Bigl (}\sum _{n=1}^{\infty }{\frac {a_{n}}{3^{n}}}{\Bigr )}\colon ={\Bigl (}\sum _{n=1}^{\infty }{\frac {a_{2n}}{3^{n}}},\sum _{n=1}^{\infty }{\frac {a_{2n+1}}{3^{n}}}{\Bigr )}\,\,$

definiert ist -- also ein mathematisches Modell des Reißverschlusses. Die Stetigkeit von ${}h$ sieht man leicht ein. Somit gibt es eine stetige surjektive Abbildung ${}(g\times g)\circ h\colon C\to I\times I$. Diese läßt sich erweitern zu einer stetigen (und erst recht surjektiven) Abbildung ${}f\colon I\to I\times I$, etwa indem in den entfernten Intervallen linear fortgesetzt wird.

Siehe auch

• FASS-Kurve
• Hilbert-Kurve
• Sierpinski-Kurve

Kurs: Topologie (Osnabrück 2008-2009) | >>