Kurs:Topologische Invertierbarkeitskriterien/Minkowski-Funktionale

Einleitung

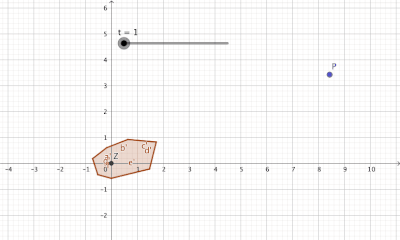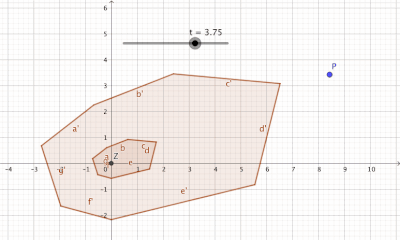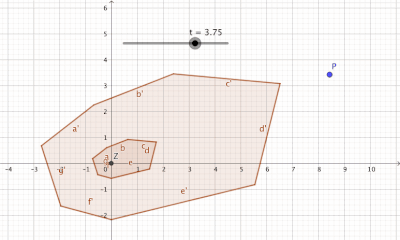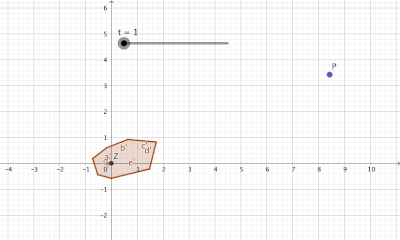
Mit absorbierenden Mengen kann man Minkowski-Funktionale definieren, wobei man mit einem Minkowski-Funktional jedem Element aus dem Vektor ein Skalar zuordnet. Diese positive reelle Zahl sagt etwas darüber aus, wie weit man ein Menge "aufblasen" muss, damit man den Vektor einfangen kann. Damit man ein Minkowski-Funktional definieren kann, benötigt man eine absorbiernde Menge, die die Eigenschaft hat, jedes Element aus dem Vektorraum durch "Aufblasen" einfangen zu können (siehe Visualisierung zu einer absorbierenden Menge).

Absorbierende Mengen

Geometrisch kann man absorbierende Menge $M$ so auffassen, dass diese durch "Aufblasen" der Menge $\lambda \cdot M$ mit einem Skalar jedes beliebiges Element $x\in V$ aus dem Vektorraum "einfangen" bzw. absorbieren kann, d.h. $x\in \lambda \cdot M:=\{\lambda \cdot m\in V\,:\,m\in M\}$ .

Visualisierung

Schwach absorbierende Menge, die mit einem Faktor $t>0$ einen Polyeder aufbläst um einen Punkt $P\in \mathbb {R} ^{2}$ einzufangen.

Definition: Absorbierende Mengen

Sei $V$ ein Vektorraum über $\mathbb {K}$ , dann heißt $M\subset V$

absorbierend, falls es für jedes $x\in V$ ein $\lambda _{x}\geq 0$ gibt mit $x\in \alpha \cdot M$ für alle $\alpha \in \mathbb {K}$ und $|\alpha |\geq \lambda _{x}$
schwach absorbierend, falls es für jedes $x\in V$ ein $\lambda _{x}\geq 0$ gibt mit $x\in \lambda _{x}\cdot M$ .

Bemerkung - Weiteres Aufblasen der Menge

Bei absorbierenden Mengen bleibt ein $x\in V$ ab einer unteren Schranke $\lambda _{x}$ für beliebig weiter "aufgeblasene" Menge $\alpha \cdot M$ mit $\lambda _{x}\leq \alpha$ weiter in der weiter aufgeblasenen Mengen (d.h. $x\in \alpha \cdot M$ .

Aufgabe - Kreisförmigkeit absorbierender Mengen

Zeigen Sie, dass eine absorbierende Menge eine kreisförmige absorbierende Teilmenge enthält.

Bemerkung - schwach absorbierende Menge

Schwach absorbierende Mengen sind nicht notwendig kreisförmig. Betrachten Sie dazu die folgenden beiden Animationen

von einem Kreisrand, der schwach absorbierend ist und
von einer Kreisscheibe, die als absorbierende Menge auch bereits eingefangene Vektoren beim weiteren Aufblasen noch enthält.

Schwach absorbierender Kreisrand

Absorbierende Kreisscheibe

Lemma: Nullumgebungen absorbierend

Sei $(V,{\mathcal {T}})$ ein topologischer Vektorraum und $U_{o}\in {\mathfrak {U}}_{\mathcal {T}}(0_{V})$ , dann ist Menge $U_{o}$ absorbierend.

Beweis

Sei Vektor $v_{0}\in V$ ein beliebiger Vektor in $V$ . Für den Beweis konstruiert man

eine $(\lambda _{n})_{n\in \mathbb {N} }$ eine Nullfolge in dem Körper $\mathbb {K}$ mit $\lambda _{n}:={\frac {1}{n}}>0$ für alle $n\in \mathbb {N}$ und
ein konstantes Netz $(v_{i})_{i\in I}$ mit $v_{i}:=v_{0}$ in $(V,{\mathcal {T}})$ , das in jeder Topologie ${\mathcal {T}}$ gegen den Vektor $v_{0}\in V$ konvergiert.

Beweis 1: Kreisförmige Nullumgebung

Damit gibt es nach dem Lemma über kreisförmige Nullumgebungen zu jeder $U\in {\mathfrak {U}}_{\mathcal {T}}(0_{V})$ eine kreisförmige Nullumgebung ${\widehat {U}}\in {\mathfrak {U}}_{\mathcal {T}}(0_{V})$ mit ${\widehat {U}}\subseteq U$ . Sei nun ${\widehat {U}}_{o}\in {\mathfrak {U}}_{\mathcal {T}}(0_{V})$ eine kreisförmige Nullumgebung zu der gegebenen Nullumgebung $U_{o}\in {\mathfrak {U}}_{\mathcal {T}}(0_{V})$ mit

{\widehat {U}}_{o}\subseteq U_{o}\in {\mathfrak {U}}_{\mathcal {T}}(0_{V})

Beweis 2: Grenzwert des Netzes

Mit der Stetigkeit der Multiplikation mit Skalaren konvergiert $(\lambda _{n}\cdot v_{i})_{i\in I}$ gegen den Nullvektor in $V$

\left(\lim _{n\to \infty }\lambda _{n}\right)\cdot \left(\lim _{i\in I}v_{i}\right)=\left(\lim _{n\to \infty }{\frac {1}{n}}\right)\cdot \left(\lim _{i\in I}v_{o}\right)=0\cdot v_{o}=0_{V}

Für dieses ${\widehat {U}}_{o}\in {\mathfrak {U}}_{\mathcal {T}}(0_{V})$ gibt es eine Indexschranke $n_{o}\in \mathbb {N}$ und eine Indexschranke $i_{o}\in I$ , sodass für alle $n\geq n_{o}$ und $i\geq i_{o}$ die folgende Bedingung gilt:

\lambda _{n}\cdot v_{i}=\lambda _{n}\cdot v_{o}\in {\widehat {U}}_{o}\subseteq U_{o}

.

Für konstante Netze ist hier die Indexschranke $i_{o}\in I$ allerdings irrelevant.

Beweis 3: Absorbierende Eigenschaft

Das konstante Netz, bei dem für alle $i\in I$ auch $v_{i}:=v_{o}$ gilt, ist konvergent gegen $v_{o}$ in jeder Topologie ${\mathcal {T}}$ . Aus $\lambda _{n}\cdot v_{o}\in {\widehat {U}}_{o}\subseteq U_{o}$ für $n\geq n_{o}$ folgt

v_{o}=\underbrace {{\frac {1}{\lambda _{n}}}\cdot \lambda _{n}} _{=1}\cdot v_{o}=n\cdot \underbrace {{\frac {1}{n}}\cdot v_{o}} _{\in {\widehat {U}}_{o}}\in n\cdot {\widehat {U}}_{o}\subseteq n\cdot U_{o}

mit

n\geq n_{o}

.

Beweis 4: Absorbierende Eigenschaft

Mit der Kreisförmigkeit von $n_{0}\cdot {\widehat {U_{o}}}$ erhält man mit $\alpha \in \mathbb {K}$ und $|\alpha |\geq n_{0}$ auch $1\geq {\frac {n_{0}}{|\alpha |}}$ :

{\frac {n_{0}}{|\alpha |}}\cdot v_{o}\in n_{0}\cdot {\widehat {U_{o}}}\subseteq n_{0}\cdot U_{o}

Beweis 5: Absorbierende Eigenschaft

Insgesamt folgt durch die Multiplikation mit ${\frac {|\alpha |}{n_{0}}}$ , dass eine ${\widetilde {\alpha }}>0$ existiert, mit dem $v_{o}$ absorbiert wird.

v_{o}\in |\alpha |\cdot U_{o}{\mbox{ mit }}{\widetilde {\alpha }}:=|\alpha |\geq n_{o}

Damit folgt die Behauptung. q.e.d.

Definition: Minkowski-Funktional

Der Menge $M$ eine absorbierende Menge in einem Vektorraum $V$ . Das Minkowski-Funktional $p_{_{M}}(x)$ der absorbierende Menge $M$ wird dabei wie folgt definiert:

p_{_{M}}(x):=\inf\{\lambda >0:x\in \lambda \cdot M\}.

Aufgaben

In den folgenden Aufgaben wird die Eigenschaft, absorbierend zu sein, überprüft. Die Definition der Minkowski-Funktionale hat besondere Bedeutung für die Definition topologieerzeugenden Funktionalen (siehe Gaugefunktionale). Daher wird für die absorbierenden Mengen auch überprüft, ob diese auch Nullumgebungen sind.

Aufgabe 1: Einheitskreisscheibe

Betrachten Sie den Vektorraum $V:=\mathbb {R} ^{2}$ mit der Einheitskreisscheibe $M_{1}:=\left\{\left({\begin{array}{c}x,y\end{array}}\right):x^{2}+y^{2}<1\right\}$ und das Quadrat $M_{2}:=\left\{\left({\begin{array}{c}x,y\end{array}}\right):|x|+|y|<1\right\}$ .

Vergleichen Sie die Minkowski-Funktionale $p_{M_{1}}(x,y)$ und $p_{M_{2}}\left({\begin{array}{c}x,y\end{array}}\right)$ und zeigen Sie, dass $p_{M_{1}}\left({\begin{array}{c}x,y\end{array}}\right)\leq p_{M_{2}}\left({\begin{array}{c}x,y\end{array}}\right)$ für alle $x\in V=\mathbb {R} ^{2}$ !
Zeigen Sie, dass $p_{M_{1}}\left({\begin{array}{c}x,y\end{array}}\right)={\sqrt {x^{2}+y^{2}}}$ .

Aufgabe 2: Einheitskreis

Betrachten Sie den Vektorraum $V:=\mathbb {R} ^{2}$ mit der Einheitskreis $M_{3}:=\left\{\left({\begin{array}{c}x,y\end{array}}\right):x^{2}+y^{2}=1\right\}$ . Überprüfen Sie, ob die Menge $M_{3}$ schwach absorbierend ist!

Aufgabe 3: Absorbierend - Nullumgebungen

Beweisen oder widerlegen Sie die Aussage: Jede schwach absorbierende Menge ist eine Nullumgebung.

Aufgabe 4:

Mit der Stetigkeit der skalaren Multiplikation in einem topologischen Vektorraum $(V,{\mathcal {T}})$ gilt nach obigem Satz, dass eine Nullumgebung eine absorbierende Menge ist. Zu jeder Nullumgebung $U$ gibt es ferner eine kreisförmige Nullumgebung ${\widehat {U}}$ mit ${\widehat {U}}\subseteq U$ .

Zeigen Sie, dass für die zugehörigen Minkowski-Funktionale die Bedingung $p_{\widehat {U}}(v)\geq p_{U}(v)$ für alle $v\in V$ gilt.
Zeigen Sie, dass für $p_{\widehat {U}}$ die Bedingung $p_{\widehat {U}}(\lambda \cdot v)=|\lambda |\cdot p_{\widehat {U}}(v)$ gilt!