Kurs:Funktionentheorie/Folgen und Reihen
Einführung
[Bearbeiten]Als Folge oder Sequenz wird in der Mathematik eine Auflistung (Familie) von endlich oder unendlich vielen fortlaufend nummerierten Objekten (beispielsweise Zahlen) bezeichnet. Dasselbe Objekt kann in einer Folge auch mehrfach auftreten. Das Objekt mit dem Index wird -tes Glied oder -te Komponente der Folge genannt. Endliche wie unendliche Folgen finden sich in allen Bereichen der Mathematik. Mit unendlichen Folgen, deren Glieder reelle Zahlen sind, beschäftigt sich vor allem die Analysis.
Folgen als Abbildungen
[Bearbeiten]Betrachtet man eine Indexmenge und einen Grundraum , aus dem die Komponenten gewählt werden, dann kann man eine Folge als Abbildung verstehen, die jedem Index ein Element aus dem Grundraum zuordnet. Folgen notiert man in der Regel (z.B.
Beispiele für Folgen
[Bearbeiten]- endliche reelle Zahlenfolge bzw. -Tupel
- ist eine reelle Zahlenfolge.
- ist eine komplexe Zahlenfolge.
Im Folgenden betrachten wir unendliche Folgen mit der Indexmenge in den komplexen Zahlen.
Konvergenz von Folgen
[Bearbeiten]Wenn auf einem Grundraum Abstände mit einer Metrik oder Längen von Vektoren mit einer Norm messen kann, kann man die Folgenkonvergenz definieren. Bei konvergenten Folgen gegen eine Grenzwert . Der Abstand der Folgenglieder zum Grenzwert läuft gegen 0.
Notation
[Bearbeiten]Für den Grenzwert einer Folge gibt es ein eigenes Symbol, man schreibt:
- mit .
Definition Folgenkonvergenz
[Bearbeiten]Sei eine komplexe Zahlenfolge und . Die Konvergenz von gegen wird dann wie folgt definiert:
- .
Notation - Schreibweise
[Bearbeiten]Neben dieser Notation ist auch die Schreibweise
- für (gelesen als konvergiert gegen für gegen unendlich) oder
- kurz bzw. üblich.
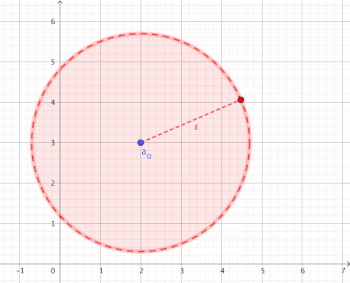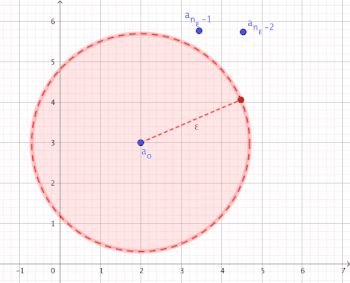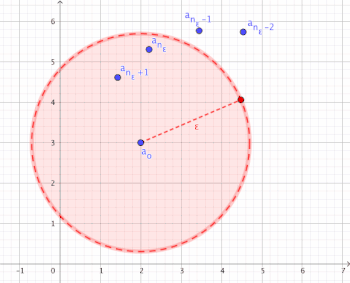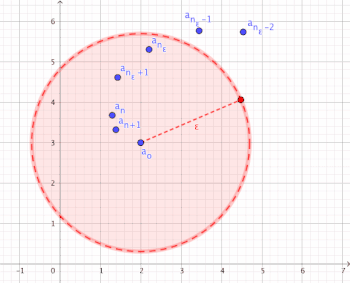
Visualisierung der Konvergenz
[Bearbeiten]Für alle gibt es eine Indexschranke , ab der alle mit in der -Umgebung liegen.
Semantik
[Bearbeiten]Die Bedeutung der Definition kann man wie folgt versprachlichen:
- .
Man kann ein beliebig kleines wählen und dennoch kann man zu diesem immer eine Indexschranke findet, sodass alle Folgenglieder mit größerem (oder gleichem) Index nicht weiter als von dem Grenzwert entfernt sind ()
Reihen
[Bearbeiten]Eine Reihe ist eine spezielle Folgen , die aus einer gegebenen Folge durch die Folge der Partialsummen mit für alle entsteht.
Konvergenz von Reihen
[Bearbeiten]Wenn auf einem Grundraum Abstände mit einer Metrik oder Längen von Vektoren mit einer Norm messen kann, kann man die Reihenkonvergenz analog zur Folgenkonvergenz definieren. Eine Reihe konvergiert, wenn die zugehörige Folge der Partialsummen konvergiert.
Absolute Konvergenz
[Bearbeiten]Eine Reihe heißt absolut konvergent, wenn die Reihe konvergiert, d.h., dass die Folge der Partialsummen konvergiert.
Aufgabe
[Bearbeiten]- Zeigen Sie, dass die komplexwertige Reihe konvergiert, aber nicht absolute konvergiert. Nutzen Sie dazu Sätze und Kenntnisse aus der reellen Analysis.
- Überprüfen Sie die folgende Reihe auf Konvergenz. Berechnen Sie die ersten Folgenglieder und tragen Sie diese in der Gaußschen Zahlenebene ein. Erläutern Sie, warum die Folge der Partialsummen diese geometrische Eigenschaften besitzt. Berechnen Sie ggf. den Grenzwert der Reihe, wenn dieser existiert.
Reihe als mathematisches Objekt
[Bearbeiten]Die Notation einer Reihe bezeichnet algebraisch keine Folge , sondern im Falle einer Konvergenz eine komplexe Zahl als Grenzwert der Folge der Partialsummen .
- mit
Notation
[Bearbeiten]Für den Grenzwert einer Reihe mit schreibt man:
Reihenkonvergenz
[Bearbeiten]Sei eine komplexe Zahlenfolge und . Die Konvergenz der Reihe bezeichnet die Konvergenz der Partialsummen gegen , d.h:
Dabei gilt .
Konvergenz von Reihen mit Koeffizienten aus einer Algebra
[Bearbeiten]Die Betrachtung von Reihenkonvergenz ist eine Spezialfall der Reihenkonvergenz in einem topologischen Vektorraum bzw. auf einer topologischen Algebra.
Topologischer Vektorraum
[Bearbeiten]Dabei liefert der topologische Vektorraum
- eine additive Verknüpfung, um Vektoren für die Partialsummen berechnen und
- eine Topologie, um auf Konvergenz der Folge von Partialsummen untersuchen zu können.
Aufgabe - Reihenkonverenz in einem topologischen Vektorraum
[Bearbeiten]Sei . Berechnen Sie den Grenzwert der Reihe als einführendes Beispiel mit den Werkzeugen der Analysis! Erläutern Sie die Gemeinsamkeiten und Unterschiede der Reihenkonvergenz in topologischen Vektorräume und dem Spezialfall . Übertragen Sie den Begriff der Konvergenz bzw. absoluten Konvergenz auf topologische Vektorräume, wenn der wie im Fall ein normierte topologischer Vektorraum ist.
Topologische Algebra - Potenzreihen
[Bearbeiten]Mit einer topologischen Algebra kann die Potenzreihenalgebra
- topologisiert werden und der topologische Abschluss der Polynomalgebra betrachtet werden
- eine Topologie wird dabei über Summation der gewichteten Vektorlängen von Kooeffizienten erzeugt, um dann die Vervollständigung des Raumes betrachten zu können,
- additive und multiplikative Verknüpfung liefert über das Cauchy-Produkt auch eine Multiplikation auf der Polynomalgebra und die Potenzreihenalgebra .
Beispiel - Polynomalgebra und Konvexkombinationen
[Bearbeiten]Betrachtet man Konvexkombinationen der Ordnung in dem Vektorraum , so stellen diese Polynome der Ordnung mit Koeffizienten in dar.
Mit CAS4Wiki kann die Spur der dreidimensionalen Konvexkombination der Ordnung 3 geplottet werden.
Literatur
[Bearbeiten]- Bourbaki: Éléments de mathématique. Theorie des Ensembles II/ III, Paris 1970
- Harro Heuser: Lehrbuch der Analysis, Teil 1, Teubner Verlag, Stuttgart
Weblinks
[Bearbeiten]- Online-Enzyklopädie der Zahlenfolgen
- Zahlenfolgen für Schüler erklärt
- Folgen von numerischen und nicht-numerischen Objekten - Primary Resources
Siehe auch
[Bearbeiten]- Folgen in der Mathematik - Wikipedia
- Gaußschen bzw. komplexe Zahlenebene
- Konvexkombination
- topologischer Vektorraum
- topologische Algebra
- Normen, Metriken, Topologie
Seiten-Information
[Bearbeiten]Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Grundlagen' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.
Wiki2Reveal
[Bearbeiten]- Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
- Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Funktionentheorie/Folgen
- siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.
Wikipedia2Wikiversity
[Bearbeiten]Diese Seite wurde auf Basis der folgenden Wikipedia-Quelle erstellt:





























































![{\displaystyle {\overline {A[t]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79a0e6de45ae9d5651c8de4255941f36e0827d8c)
![{\displaystyle A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13daf73f25e64310e7e5d67c5aa8dd4f97cb884f)

