Kurs:Topologische Invertierbarkeitskriterien/Einführung

Algebra

Zunächst betrachten man einen Vektorraum $(A,+,\cdot )$ über einem Körper $\mathbb {K}$ auf dem zusätzliche eine multiplikative Verknüpfung $\odot :A\times A\rightarrow A$ definiert ist (siehe Topologische Algebra).

Algebraerweiterung

Das grundlegende Prinzip der Vorgehensweise ist die Untersuchung von Eigenschaften in Erweiterungen einer gegebenen topologischen Algebra. Dabei ist die Algebra ${\textstyle B}$ eine Erweiterung der Algebra ${\textstyle A}$, falls sich ${\textstyle A}$ durch einen Algebramonomorphismus in geeigneter topologischer und algebraischer Weise in ${\textstyle B}$ eingebetten lässt. Im allgemeinen identifiziert man ${\textstyle A}$ mit der Einbettung und schreibt ${\textstyle A\subset B}$.

Invertierbarkeit in Erweiterungen

Es stellt sich die Frage, ob ein bestimmtes Element $z\in A$, das unter Umständen in $A$ nicht invertierbar ist, in einer vergrößerten Algebra $B$ ein inverses Element $b\in B$ besitzt.

$e=z\cdot b=b\cdot z$

Die Multiplikation ist dabei nicht notwendig kommuntativ (wie z.B. bei der Matrixmultiplikation)

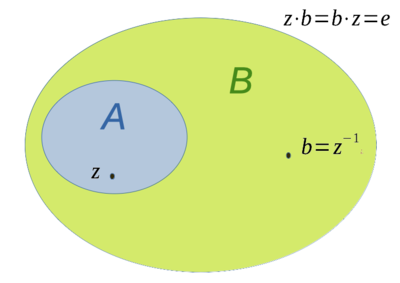
Veranschaulichung

Algebraerweiterung $B$ von $A$, die ein inverses Element $b=z^{-1}\in B$ zu einem gegeben $z\in A$ enthält.

Geschichte

Die grundlegende Idee, Invertierbarkeit in Algebraerweiterungen zu untersuchen, stammt von Arens, wobei zunächst Algebraerweiterungen von normierten Algebren untersucht wurden. Zelazko hat dieses Konzept aufgegriffen und das auf lokalkonvexe Algebren übertragen.

Neutrales Element der Multiplikation

Dabei ist $e\in A$ das neutrale Element (Einselement) der Multiplikation in $A$ und jeder Erweiterung $B$ von $A$.

Topologisches Invertierbarkeitskriterium

Dieser Sachverhalt soll dann über ein topologisches Kriterium für $z\in A$ beschrieben werden, das äquivalent zur Invertierbarkeit in einer bestimmten Algebraerweiterung von $A$ ist und nur von der Topologie der Algebra $A$ allein abhängig ist; d.h. die Lösbarkeit der Gleichung

$e=z\cdot b=b\cdot z$

durch ein Element $b\in B$ und dem Einselement der Multiplikation $e\in A$ lässt sich unmittelbar über die topologischen Eigenschaften von $z\in A$ entscheiden.

Beweisrichtungen für Invertierbarkeitskriterien

Um ein topologisches Invertierbarkeitskriterium zu erhalten, sind prinzipiell zwei Beweisrichtungen zu zeigen. Zum einen ist nachzuweisen, dass jedes Element $z\in A$, das in einer Algebraerweiterung invertierbar ist, das topologische Kriterium erfüllt und zum anderen muss man mit diesem Kriterium eine Algebraerweiterung konstruieren können, in der $z\in A$ invertierbar ist.

Invertierbarkeitskriterien für Algebrenklassen

Die Invertierbarkeitskriterien werden wegen ihrer Abhängigkeit von der zugrundeliegenden Topologie für bestimmte Klassen ${\textstyle {\mathcal {K}}}$ von Algebren getrennt betrachtet. Jede Banachalgebra ist zugleich auch eine lokalkonvexe Algebra. Daher ist es möglich, dass ein $z\in A$ aus einer Banachalgebra ggf. in jeder Banachalgebraerweiterung singulär ist aber u.U. in eine lokalkonvexen Algebraerweiterung ein inverses Element besitzt. Daher werden die Invertierbarkeitskriterien für Algebrenklassen getrennt untersucht.

Algebrenklassen

• ${\textstyle {\mathcal {B}}}$ - Klasse der Banachalgebren,
• ${\textstyle {\mathcal {P}}}$ - Klasse der lokalbeschränkten Algebren,
• ${\textstyle {\mathcal {LC}}}$ - Klasse der lokalkonvexen Algebren,
• ${\textstyle {\mathcal {MLC}}}$ - Klasse der multiplikativ lokalkonvexen Algebren,
• ${\textstyle {\mathcal {PC}}}$ - Klasse der pseudokonvexen Algebren,
• ${\textstyle {\mathcal {MPC}}}$ - Klasse der multiplikativ pseudokonvexen Algebren,
• ${\textstyle {\mathcal {T}}}$ - Klasse aller topologischen Algebren.

K-singulär - K-regulär

Die Invertierbarkeit in Algebraerweiterung hängt von der betrachteten Klasse ${\mathcal {K}}$ von Algebren ab. Daher werden die Begriffe ${\mathcal {K}}$-singulär und ${\mathcal {K}}$-regulär verwendet.

Permanent singulär - K-singulär

Wenn die untersuchte Algebrenklasse ${\mathcal {K}}$ für den Lernenden klar ist, nennt man ein $z\in A\in {\mathcal {K}}$ permanent singulär, wenn $z$ in jeder Algebraerweiterung $B\in {\mathcal {K}}$ der Algebrenklasse ${\mathcal {K}}$ nicht invertierbar (singulär) ist. Betrachtet man in einem Kontext unterschiedliche Algebrenklassen wird ein Element $z\in A\in {\mathcal {K}}$ zur genaueren Unterscheidung ${\mathcal {K}}$-singulär genannt.

K-regulär

Wenn man zu einem $z\in A\in {\mathcal {K}}$ eine Algebraerweiterung $B$ der Klasse ${\mathcal {K}}$ finden kann, in der ein inverses Element $b\in B\in {\mathcal {K}}$ zu $z\in A$ existiert, so nennt man $z$ ${\mathcal {K}}$-regulär.

Beispiel

Die Menge der Banachalgebren ${\mathcal {B}}$ ist in der Menge der lokalkonvexen Algebren ${\mathcal {LC}}$ enthalten. Ist ein Element $z\in A\in {\mathcal {B}}\subset {\mathcal {LC}}$ z.B. ${\mathcal {LC}}$-singulär, so ist es auch ${\mathcal {B}}$-singulär, weil die Algebrenklasse ${\mathcal {LC}}$ auch alle potentiellen Banachalgebraerweiterung aus ${\mathcal {B}}$ enthält, in denen $z\in A\in {\mathcal {B}}$ invertierbar sein könnte.

Wesentliche Schritte

• Topologisierungslemma sorgt dafür, dass man sich in topologischen Algebren $(A,{\mathcal {T}})$ nicht mehr mit dem System von offenen Menge für die Aussagen auf der topologischen Algebra beschäftigen muss, sondern nur noch mit topologieerzeugenden Gaugefunktionalen (z.B. einem Halbnormensystem).
• Polynomalgebra $A[t]$ mit Koeffizienten aus der gegebenen Algebra $(A,{\mathcal {T}})$ liefert einen wesentliches Konstruktionselement für die gesuchte Algebra $B$, in der eine gegebenes $z\in A$ ein Inverses Element besitzt.

Lösbarkeit von Gleichungen

Die Invertierbarkeitsgleichung, bei der man nach einem inversen Element $b\in B$ sucht, das die Gleichung $z\cdot b=e$ löst, kann man auf eine allgemeinere Fragestellung zurückführen, die ein topologisches Kriterium der Lösbarkeit Gleichung

$z_{1}\cdot b=z_{2}$ mit $z_{1},z_{2}\in A$

für ein $b\in B$ aus einer Algebraerweiterung $B$ von $A$ liefert.

Aufgaben

In einem ersten Schritt lernen wird bereits permanent singuläre Elemente kennen, die durch ihre algebraischen Eigenschaften NIE ein inverses Element in Algebraerweiterungen besitzen können. Die drei Aussagen über die permanent singulären Elemente gelten unabhängig von der Algebrenklasse ${\mathcal {K}}$ der topologischen Algebra $A\in {\mathcal {K}}$. Führen Sie den Beweis durch Widerspruch!.

Permanent singuläre Elemente

• (Nullvektor) Sei $0_{A}\in A$ der Nullvektor aus der Algebra $A$, zeigen Sie, dass $0_{A}\in A$ permanent singulär ist.
• (Nullteiler) Sei $z\in A$ ein Nullteiler der Algebra $A$, zeigen Sie, dass $z\in A$ permanent singulär ist.
• (Nilpotentes Element) Sei $z\in A$ nilpotent in der Algebra $A$, d.h. es gibt ein $n\in \mathbb {N}$ mit $z^{n}=0_{A}$ und $0_{A}\in A$ ist der Nullvektor in $A$. Ist ferner $z^{n-1}\not =0_{A}$ mit $n\in \mathbb {N}$, so ist $z\in A$ nilpotent mit der Ordnung $n$. Zeigen Sie, dass $z\in A$ mit $n\in \mathbb {N}$ permanent singulär ist (V1: direkt mit Beweis durch Widerspruch V2: nilpotente Elemente sind auch Nullteiler).

Siehe auch

• Topologische Algebra
• Algebraerweiterung
• Vektorräume
• Banachalgebra
• Nullteiler
• Nilpotentes Element und nilpotente Matrix

Seiteninformation

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Topologische Invertierbarkeitskriterien' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

• Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
• Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Topologische%20Invertierbarkeitskriterien/Einf%C3%BChrung
• siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.