Kurs:Topologische Invertierbarkeitskriterien/Algebraerweiterung

Zielsetzung

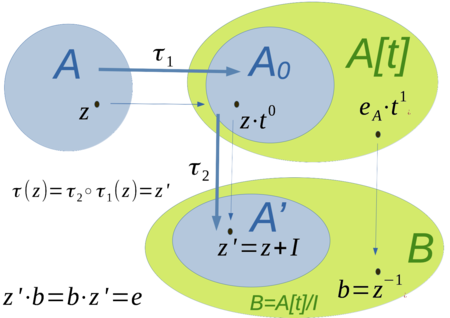
Zielsetzung einer Algebraerweiterung $(B,{𝒯}_B)$ zu einer gegebenen topologischen Algebra $(A,{𝒯}_A)$ mit $z\in A$ ist es, die topologisch Algebra so zu vergrößern, dass diese ein inverses Element $z^{-1}:=b\in B$ enthält. Das folgenden Diagramm veranschaulicht den Sachverhalt:

Veranschaulichung

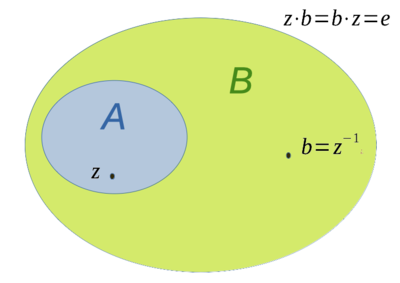
Algebraerweiterung $B$ von $A$, die ein inverses Element $b=z^{-1}\in B$ zu einem gegebenen $z\in A$ enthält.

Algebraerweiterung - Zahlbereichserweiterung

Untersuchen Sie die Gemeinsamkeiten und Unterschiede bzgl. Algebraerweiterungen in der Funktionalanalysis und den Zahlbereichserweiterungen im Kontext der Schule.

Unlösbare Aufgaben in der Primarstufe

In der Primarstufe können in dem Zahlbereich der natürlichen Zahlen ${\mathbb{N}}_0$ Aufgaben formuliert werden, die aber in ${\mathbb{N}}_0$ nicht lösbar sind. Daraus ergibt sich eine Zahlbereichserweiterung wie folgt:

• ($\mathbb{N}\mapsto \mathbb{Z}$) Aufgabe $6+◻=4$ (bzw. $6+x=4$) in $\mathbb{N}$ formuliert aber in $\mathbb{N}$ nicht lösbar. Zahlbereichserweiterung auf $\mathbb{Z}$.
• ($\mathbb{N}\mapsto \mathbb{Q}$) Aufgabe $6\cdot ◻=4$ (bzw. $6\cdot x=4$) in $\mathbb{N}$ formuliert aber in $\mathbb{N}$ nicht lösbar. Zahlbereichserweiterung auf $\mathbb{Q}$.
• ($\mathbb{N}\mapsto \mathbb{Q}$) Zu diesem unlösbaren Aufgabentyp gehören auch die multiplikativen Inversen, z.B. $5\cdot ◻=1$.

Unlösbare Aufgaben in der Sekundarstufe

Die unlösbaren Aufgaben ergeben sich aus quadratischen Gleichungen

• ($\mathbb{Q}\mapsto ℝ$) Aufgabe $x^2=2$ in $\mathbb{Q}$ formuliert aber in $\mathbb{Q}$ nicht lösbar. Zahlbereichserweiterung auf $ℝ$.
• ($ℝ\mapsto ℂ$) Aufgabe $x^2=-1$ in $ℝ$ formuliert aber in $ℝ$ nicht lösbar. Zahlbereichserweiterung auf $ℂ$ (siehe auch komplexe Zahlen).

Analogien und Unterschiede

Welche Gemeinsamkeiten und Unterschiede bestehen zwischen den Zahlbereichserweiterungen in der Schule und den Algebraerweiterungen und der Untersuchung von topologischen Invertierbarkeitskriterien?

Definition: Algebrahomomorphismus

Seien $(A,{\oplus }_{{}_A},{\odot }_{{}_A},{\cdot }_{{}_A},𝕂)$ und $(B,{\oplus }_{{}_B},{\odot }_{{}_B},{\cdot }_{{}_B},𝕂)$ zwei Algebren über dem Körper $𝕂$ und $\tau :A\to B$ eine Abbildung von $A$ nach $B$. $\tau :A\to B$ heißt Algebrahomomorphismus die $\tau$ verträglich mit den Verknüpfungen auf der Algebra ist, d.h.:

• (AH1) Für alle $x\in A$, $\lambda \in 𝕂$ gilt: $\tau (\lambda {\cdot }_{{}_A}x)=\lambda {\cdot }_{{}_B}\tau (x)$
• (AH2) Für alle $x,y\in A$ gilt: $\tau (x{\oplus }_{{}_A}y)=\tau (x){\oplus }_{{}_B}\tau (y)$
• (AH3) Für alle Für alle $x,y\in A$ gilt: $\tau (x{\odot }_{{}_A}y)=\tau (x){\odot }_{{}_B}\tau (y)$

Wenn der Algebrahomomorphismus zusätzlich bijektiv ist, nennt man $\tau$ Algebraisomorphismus.

Bemerkung: Notation für die inneren Verknüpfungen in den Algebren

Der Index bei den inneren Verknüpfungen bezeichnet die Algebren, auf denen die inneren Verknüpfungen definiert sind. In der Regel werden die Bezeichnungen bei Algebraerweiterung durch Notation nicht unterschieden.

Definition: Algebraerweiterung

Sei ${𝒦}_e$ eine Klasse von unitalen Algebren und $A\in {𝒦}_e$, dann heißt $B\in {𝒦}_e$ Algebraerweiterung, Oberalgebra oder $𝒦$-Erweiterung von $A$, falls es einen Algebraisomorphismus $\tau :A⟶A^{\prime }\subset B$ gibt mit:

• $\tau (e_{{}_A})=e_{{}_B}$, wobei $e_{{}_A}$ ist das Einselement von $A$ und $e_{{}_B}\in A^{\prime }$ das Einselement von $B$ ist.
• $A$ ist homöomorph zu $A^{\prime }$; d.h. $\tau$ und ${\tau }^{-1}:A^{\prime }⟶A$ sind stetig.

Bemerkung - unitale Algebren

Eine topologische Algebra $A\in {𝒦}_e$ der Klasse $𝒦$ heißt unital, wenn $A$ ein Einselement der Multiplikation besitzt. Der Begriff kommt von "unit" als "Einheit" bzw. "Einselement".

Bemerkung

• Im allgemeinen identifiziert man $A$ mit $A^{\prime }\subset B$ und schreibt $A\subset B$.
• Sei ${𝔘}_{A^{\prime }}(0)$ eine Nullumgebungsbasis der Relativtopologie von $B$ auf $A^{\prime }$ und ${𝔘}_A(0)$ eine Nullumgebungsbasis von $A$, dann kann man die Homöomorphie zwischen $A$ und $A^{\prime }$ wie folgt beschreiben:

$\begin{array}{ccc}{\mathrm{\forall }}_{V\in {𝔘}_{A^{\prime }}(0)}{\mathrm{\exists }}_{U\in {𝔘}_A(0)}& :& U\subset V(\tau (U)\subset V)\\ {\mathrm{\forall }}_{U\in {𝔘}_A(0)}{\mathrm{\exists }}_{V\in {𝔘}_{A^{\prime }}(0)}& :& V\subset U({\tau }^{-1}(V)\subset U).\end{array}$

Stetigkeit und Minkowskifunktionale

Betrachtet man die Minkowskifunktionale ${\Vert \cdot \Vert }_{{𝔘}_{A^{\prime }}}$ und ${\Vert \cdot \Vert }_{{𝔘}_A}$ für Nullumgebungen, so lassen sich die oberen beiden Aussagen wie folgt umformulieren (siehe auch Stetigkeitssatz für lineare Abbildungen):

$\begin{array}{ccc}{\mathrm{\forall }}_{V\in {𝔘}_A(0)}{\mathrm{\exists }}_{U\in {𝔘}_{A^{\prime }}(0)}& :& {\Vert \cdot \Vert }_V\le {\Vert \cdot \Vert }_U\\ \text{ bzw. }& & {\Vert \cdot \Vert }_V\circ \tau \le {\Vert \cdot \Vert }_U\\ {\mathrm{\forall }}_{U\in {𝔘}_{A^{\prime }}(0)}{\mathrm{\exists }}_{V\in {𝔘}_A(0)}& :& {\Vert \cdot \Vert }_U\le {\Vert \cdot \Vert }_V\\ \text{ bzw. }& & {\Vert \cdot \Vert }_U\circ {\tau }^{-1}\le {\Vert \cdot \Vert }_V.\end{array}$

Bemerkung Topologieerzeugung

Falls in einem topologieerzeugenden System von Minkowskifunktionalen ${\Vert \cdot \Vert }_{𝒜}$ nicht mit jedem ${\Vert \cdot \Vert }_{\alpha }$ auch $\lambda \cdot {\Vert \cdot \Vert }_{\alpha }$ in dem System ${\Vert \cdot \Vert }_{𝒜}$ liegt, treten in der Ungleichung jeweils von $U$ bzw. $V$ abhängige Konstanten auf.

Definition: Äquivalenz von Gaugefunktionalsystemen

Sei $A$ eine Algebra, auf der zwei topologieerzeugende Systeme von Gaugefunktionalen ${\Vert \cdot \Vert }_{𝒜}$ bzw. ${\Vert |\cdot |\Vert }_{\widetilde{𝒜}}$ definiert sind. Die beiden Gaugefunktionalsystem heißen äquivalent, wenn für diese gilt:

$${\mathrm{\forall }}_{\alpha \in 𝒜}{\mathrm{\exists }}_{\beta \in \widetilde{𝒜},C_{\beta }>0}{\mathrm{\forall }}_{x\in A}:{\Vert x\Vert }_{\alpha }\le C_{\alpha }\cdot {\Vert \left|x\right|\Vert }_{\beta }$$

und umgekehrt

$${\mathrm{\forall }}_{\beta \in \widetilde{𝒜}}{\mathrm{\exists }}_{\alpha \in 𝒜,C_{\alpha }>0}{\mathrm{\forall }}_{x\in A}:{\Vert |x\Vert |}_{\beta }\le C_{\beta }\cdot {\Vert x\Vert }_{\alpha }.$$

Bemerkung: Implikation der Konvergenz

• Die erste Bedingung in der obigen Definition liefert, dass ein Netz $(x_i{)}_{i\in I}$, das bzgl. ${\Vert |\cdot |\Vert }_{\widetilde{𝒜}}$ konvergiert auch in der von ${\Vert \cdot \Vert }_{𝒜}$ erzeugten Topologie konvergiert.
• Die zweite Bedingung liefert umgekehrt, dass $(x_i{)}_{i\in I}$ bzgl. ${\Vert |\cdot |\Vert }_{\widetilde{𝒜}}$ konvergiert, wenn das Netz auch bzgl. ${\Vert \cdot \Vert }_{𝒜}$ konvergiert.

Definition: isometrische Erweiterung von Gaugefunktionalsystemen

Sei $B$ eine $𝒯$-Algebraerweiterung von $A\in 𝒯$ mit den topologieerzeugenden Systemen von Gaugefunktionalen ${\Vert \cdot \Vert }_{𝒜}$ auf $A$ bzw. ${\Vert |\cdot |\Vert }_{\widetilde{𝒜}}$ auf $B$. Die Algebraerweiterung nennt isometrisch, falls gilt:

$${\mathrm{\forall }}_{\alpha \in 𝒜}{\mathrm{\exists }}_{\beta \in \widetilde{𝒜}}{\mathrm{\forall }}_{x\in A}:{\Vert x\Vert }_{\alpha }={\Vert \left|x\right|\Vert }_{\beta }$$

und umgekehrt

$${\mathrm{\forall }}_{\beta \in \widetilde{𝒜}}{\mathrm{\exists }}_{\alpha \in 𝒜}{\mathrm{\forall }}_{x\in A}:{\Vert \left|x\right|\Vert }_{\alpha }={\Vert x\Vert }_{\beta }.$$

Definition: K-regulär - K-singulär

Sei ${𝒦}_e$ eine Klasse topologischer Algebren mit Einselement und $A\in {𝒦}_e$ eine Algebra. Ein Element $x$ der Algebra $A$ heißt $𝒦$-regulär (Bezeichnung: $x\in {𝒢}_{𝒦}(A)$), falls es eine $𝒦$-Erweiterung $B$ von $A$ gibt, in der $x$ invertierbar ist. Falls dies nicht möglich ist, heißt $x$ $𝒦$-singulär oder permanent singulär in jeder $𝒦$-Erweiterung von $A$.

Bemerkung: Polynomalgebra

Bei der Konstruktion der Algebraerweiterung ist es für einige Algebrenklassen notwendig, die Erweiterung auf die Algebra der Polynome $A[t]$ zu betrachten. Die folgende Abbildung zeigt, wie die Algebraerweiterung $B$ konstruiert wird.

Bemerkung: regulär - K-regulär

Jedes reguläre Element $z\in A$ ist zugleich auch $𝒦$-regulär, da reguläre Elemente bereits in der Algebra $(A,{𝒯}_A)$ selbst invertierbar sind, $(A,{𝒯}_A)$ in natürlicher Weise eine Algebraerweiterung von sich darstellt, in der das inverse Element $z^{-1}\in B:=A$ existiert. Daher gilt $𝒢(A)\subset {𝒢}_{𝒦}(A)$.

Definition: Absolutcharakter

Die $𝒦$-Singularität besitzt Absolutcharakter, falls aus $𝒦$-Singularität $𝒯$-Singularität folgt.

Augaben für Lernende

Die Aufgaben beziehen sich auf die topologieerzeugenden Gaugefunktionalsysteme und die Äquivalenz dieser Systeme. Diese Äquivalenz der Gaugefunktionalsysteme wird für die Einbettung der Algebraerweiterung von $A$ in $B$ benötigt, damit man die Stetigkeit der Einbettung $\tau$ und der Umkehrabbildung ${\tau }^{-1}$ nachweisen kann.

Aufgabe 1: Bezug unter Unterschiede zum Satz von Hahn-Banach

Betrachten Sie den Satz von Hahn-Banach und die Erweiterung von linearen Funktionalen $f$ von einem Unterrraum $U\subset V$ auf den gesamten Vektorraum $V$.

• Welche topologischen Gemeinsamkeiten und Unterschiede sehen Sie bei der Erweitung von linearen Funktionalen (Hahn-Banach) und der Algebraerweiterung?
• Wie kann man aus einem linearen Funktional $f$ ein Halbnorm $\Vert \cdot {\Vert }_f$ auf $U\subset V$ erzeugen und mit der Erweiterung von $F$ auf $V$ eine Halbnorm auf $V$?

Aufgabe 2: Konvergenz in äquivalenten Gaugefunktionalsystemen

Sei $A$ eine Algebra, auf der zwei topologieerzeugende Systeme von Gaugefunktionalen ${\Vert \cdot \Vert }_{𝒜}$ bzw. ${\Vert |\cdot |\Vert }_{\widetilde{𝒜}}$ definiert sind. Ferner sei ein Netz in gegeben.

• Notieren Sie dazu zunächst die Konvergenz bzgl. der topologieerzeugende Systeme von Gaugefunktionalen ${\Vert \cdot \Vert }_{𝒜}$ und ${\Vert |\cdot |\Vert }_{\widetilde{𝒜}}$ formal.
• Zeigen Sie, dass in einer Algebra $A$ ein Netz genau der dann in ${\Vert \cdot \Vert }_{𝒜}$ konvergiert, wenn es auch bzgl. ${\Vert |\cdot |\Vert }_{\widetilde{𝒜}}$ konvergiert.

Aufgabe 3: Algebraerweiterungen von Matrixalgebren

Sei $(A,\Vert \cdot \Vert )$ die nicht-kommunitive Algebra der 2x2-Matrizen über $ℝ$ mit der euklidischen Norm:

$\Vert M\Vert =\Vert \left(\begin{array}{cc}{m}_1& m_2\\ m_3& m_4\end{array}\right)\Vert :=\sqrt{\sum _{k=1}^4{m}_k^2}$

Aufgabe 3a: Polynomalgebraerweiterungen von Matrixalgebren

Erzeugen Sie eine Polynomalgebra mit Koeffizienten in $A$ und topologisieren Sie den Raum $A[t]$ ebenfalls mit einer Norm.

Definition 3b: Matrxixalgebraerweiterungen von Matrixalgebren

Betten Sie $(A,\Vert \cdot \Vert )$ in den Raum $(B,\Vert \cdot {\Vert }_B)$ der 3x3-Matrizen über $ℝ$ ein.

$\Vert N{\Vert }_B={\Vert \left(\begin{array}{ccc}{n}_1& n_2& n_3\\ n_4& n_5& n_6\\ n_7& n_8& n_9\end{array}\right)\Vert }_B:=\sqrt{\sum _{k=1}^9{n}_k^2}\text{ mit }\tau (M):=\left(\begin{array}{ccc}{m}_1& m_2& 0\\ m_3& m_4& 0\\ 0& 0& \frac{m_1+m_4}{2}\end{array}\right)\in B$

Aufgabe 3c: Matrixalgebraerweiterungen von Matrixalgebren

Ist über die mit $\tau$ definierte Abbildung eine Algebraerweiterung definiert worden? Überprüfen Sie die Eigenschaften!

• Zeigen Sie, dass $\tau :A\to A^{\prime }\subset B$ bijektiv $(A,\Vert \cdot \Vert )$ nach $(A^{\prime },\Vert \cdot {\Vert }_B)$ ist.
• Verwenden Sie den Stetigkeitssatz für lineare Abbildungen, um die Stetigkeit von $\tau :A\to A^{\prime }\subset B$ und ${\tau }^{-1}:A^{\prime }\to A$ nachzuweisen.
• Können Sie ein Element in der ursprünglichen Algebra $(A,\Vert \cdot \Vert )$ der $2\times 2$-Matrizen angeben, das in $A$ nicht invertierbar ist, aber bei dem Sie in ein inverses Element aus $B$ nach der Einbettung angeben können? (Hinweis: Sind nicht-invertierbare Matrizen Nullteiler in $A$?)

Siehe auch

• Relativtopologie
• Topologische Algebra
• Konvexkombinationen
• Stetigkeitssatz für lineare Abbildungen
• Stetigkeitssequenzen
• Topologische Gruppe

Seiteninformation

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Topologische Invertierbarkeitskriterien' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

• Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
• Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Topologische%20Invertierbarkeitskriterien/Algebraerweiterung
• siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.