Wenn wir die  -Regularität eines Elementes
-Regularität eines Elementes  für eine multiplikativ lokalkonvexe topologische Algebra
für eine multiplikativ lokalkonvexe topologische Algebra  sprechen, suchen wir nach einer multiplikativ lokalkonvexen Algebraerweiterungen
sprechen, suchen wir nach einer multiplikativ lokalkonvexen Algebraerweiterungen  von
von  in der
in der  invertierbar ist. Dabei besteht
invertierbar ist. Dabei besteht
 und
und
aus einem System von submultiplikativen Halbnormen, die die Topologie auf  bzw.
bzw.  erzeugen.
erzeugen.
Zielsetzung einer multiplikativ lokalkonvexe Algebraerweiterung  zu einer gegebenen topologischen Algebra
zu einer gegebenen topologischen Algebra  mit
mit  ist es, die gegebene multiplikativ lokalkonvexe Algebraerweiterung so zu vergrößern, dass diese ein inverses Element
ist es, die gegebene multiplikativ lokalkonvexe Algebraerweiterung so zu vergrößern, dass diese ein inverses Element  in der multiplikativ lokalkonvexen Algebraerweiterung
in der multiplikativ lokalkonvexen Algebraerweiterung  besitzt. Als topologieerzeugende
besitzt. Als topologieerzeugende  -Gaugefunktionale werden hier Halbnormensystem
-Gaugefunktionale werden hier Halbnormensystem  und
und  verwendet.
verwendet.
Für kommutative multiplikativ lokalkonvexe Algebren  mit unital positivem System von erhält man folgende Charakterisierung:
mit unital positivem System von erhält man folgende Charakterisierung:

 -singulär
-singulär 
 (multiplikativer topologischer Nullteiler)
(multiplikativer topologischer Nullteiler)
 -regulär
-regulär  für alle
für alle  und ein
und ein  mit
mit  für alle
für alle 
Dabei sind  submultiplikative Halbnormen.
submultiplikative Halbnormen.
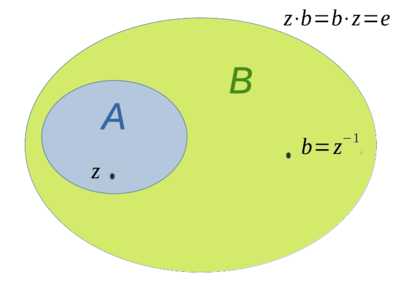
Algebraerweiterung  von
von  ist hier eine mulitplikative lokalkonvexe Algebra, die ein inverses Element
ist hier eine mulitplikative lokalkonvexe Algebra, die ein inverses Element  zu einem gegebenen
zu einem gegebenen  enthält.
enthält.
- Negieren Sie die Aussage, dass
 kein topologischer Nullteiler ist und formulieren
kein topologischer Nullteiler ist und formulieren  für ein submultiplikative Halbnormensystem
für ein submultiplikative Halbnormensystem  .
.
- Zeigen Sie, dass in einer
 -Algebra mit
-Algebra mit 
 -regulär ist, wenn folgende Bedingung gilt (siehe Zelazko 1971[1])
-regulär ist, wenn folgende Bedingung gilt (siehe Zelazko 1971[1])
 .
.
- Zeigen Sie mit der Charakterisierung der
 -Regularität, dass die
-Regularität, dass die  -singulären Elemente genau die topologischen Nullteiler sind.
-singulären Elemente genau die topologischen Nullteiler sind.
Multiplikative lokalkonvexe Algebraerweiterung
[Bearbeiten]Sei  die Klasse der multiplikativen lokalkonvexen unitalen Algebren und
die Klasse der multiplikativen lokalkonvexen unitalen Algebren und  . Die Algebraerweiterung
. Die Algebraerweiterung  bzw.
bzw.  -Erweiterung von
-Erweiterung von  benötigt nach Definition es einen Algebraisomorphismus
benötigt nach Definition es einen Algebraisomorphismus
 mit:
mit:
 , wobei
, wobei  ist das Einselement von
ist das Einselement von  und
und  das Einselement von
das Einselement von  ist.
ist. ist homöomorph zu
ist homöomorph zu  ; d.h.
; d.h.  und
und  sind stetig.
sind stetig.
Algebraisomorphismus in den Quotientenräumen
[Bearbeiten]Der Algebraisomorphismus wird über normierte Quotientenalgebren  definiert. wobei mit :
definiert. wobei mit : mit
mit ![{\displaystyle \tau _{\alpha }(x)=[x]_{\alpha }\in A'_{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c79230820ee51cceb0d1ab03aad2f6cfabadeafa) bezeichnet und
bezeichnet und

Algebraerweiterung von MLC-Quotientenalgebren
[Bearbeiten]
Embettung in Quotientenräume bzgl. der submultiplikativen Halbnormen.
Algebraisomorphismus - Einbettung in die Algebraerweiterung
[Bearbeiten]- Im allgemeinen identifiziert man
 mit
mit  und schreibt
und schreibt  . In der jeweiligen Konstruktion der Algebraerweiterung sieht man, dass die Element aus
. In der jeweiligen Konstruktion der Algebraerweiterung sieht man, dass die Element aus  mit Elementen
mit Elementen  in einem Quotientenraum
in einem Quotientenraum ![{\displaystyle B:=A[t]/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bc806fa49af6a80a0b8ba7a4eb54a8d503dd8ab) identifiziert werden.
identifiziert werden.
- Sei
 eine Nullumgebungsbasis der Relativtopologie von
eine Nullumgebungsbasis der Relativtopologie von  auf
auf  und
und  eine Nullumgebungsbasis von
eine Nullumgebungsbasis von  , dann kann man die Homöomorphie zwischen
, dann kann man die Homöomorphie zwischen  und
und  wie immer über die Topologie ausdrücken:
wie immer über die Topologie ausdrücken:

Betrachtet man die Halbnormen  und
und  für Nullumgebungen, so lassen sich die oberen beiden Aussagen wie folgt umformulieren (siehe auch Stetigkeitssatz für lineare Abbildungen):
für Nullumgebungen, so lassen sich die oberen beiden Aussagen wie folgt umformulieren (siehe auch Stetigkeitssatz für lineare Abbildungen):

Für die Konstruktion des Algebraisomorphismus geht man wie folgt vor:
- (KA1) man konstruiert zunächst einen Algebrahomomorphismus
 und zeigt, dass dieser stetig ist.
und zeigt, dass dieser stetig ist.
- (KA2) man zeigt, dass der Algebrahomomorphismus injektiv ist

- (KA3) man definiert mit
 , die Umkehrabbildung
, die Umkehrabbildung  und zeigt, dass
und zeigt, dass  ebenfalls stetig ist (siehe Stetigkeitssatz für lineare Abbildungen).
ebenfalls stetig ist (siehe Stetigkeitssatz für lineare Abbildungen).
Verwendung der Charakterisierung B-regulärer Elemente
[Bearbeiten]Wir betrachten zunächst multiplikativ lokalkonvexe kommuntative Algebren  und nutzen die Charakterisierung
und nutzen die Charakterisierung  -Regularität für die
-Regularität für die  -Erweiterung von
-Erweiterung von  .
.
Ohne Einschränkung seien die submultiplikativen Halbnormen unital positiv, d.h.  für alle
für alle  . Falls das nicht der Fall ist, geht man zu einem äquivalenten Halbnormensystem über
. Falls das nicht der Fall ist, geht man zu einem äquivalenten Halbnormensystem über  über. Weil
über. Weil  Hausdorffraum ist, gibt es ein
Hausdorffraum ist, gibt es ein  mit
mit  . Man definiert dann
. Man definiert dann  und
und

als Minkowski-Funktional von  und
und  , da
, da  und damit auch
und damit auch  submultiplikativ sind.
submultiplikativ sind.
 ist eine offene Menge in
ist eine offene Menge in  , da
, da  als Schnitt von zwei offenen Mengen definiert ist und der endliche Schnitt von offenen Mengen in einer Topologie ist wieder offen.
als Schnitt von zwei offenen Mengen definiert ist und der endliche Schnitt von offenen Mengen in einer Topologie ist wieder offen.
Aufgabe - Äquivalenz des Halbnormensystems - unital positiv
[Bearbeiten]Zeigen Sie, dass die Halbnormensysteme  und
und  äquivalente Gaugefunktionalsysteme sind!
äquivalente Gaugefunktionalsysteme sind!
Aufgabe - TNT-Negation und unital positives Halbnormensystem
[Bearbeiten]Ohne Einschränkung sei das gegebene Halbnormensystem  auf einer unital positiven
auf einer unital positiven  -Algebra
-Algebra  . Ferner sei
. Ferner sei  kein topologischer Nullteiler (
kein topologischer Nullteiler ( ). Zeigen Sie, dass für alle
). Zeigen Sie, dass für alle  ebenfalls
ebenfalls  gilt.
gilt.
Topologische Nullteiler in MLC-Algebren
[Bearbeiten]Wenn  erfüllt ist, gibt es ein
erfüllt ist, gibt es ein  , sodass für alle
, sodass für alle  gilt
gilt

Topologische Nullteiler in Quotientenalgebren
[Bearbeiten]Damit ist insbesondere für  mit
mit  (d.h.
(d.h.  für alle
für alle  die folgende Bedingung erfüllt
die folgende Bedingung erfüllt

Abschätzung für Eigenschaft in Quotientenalgebren 1
[Bearbeiten]Man erhält die folgenden Abschätzung für  , d.h.
, d.h.  für alle
für alle  und alle
und alle  :
:

Abschätzung für Eigenschaft in Quotientenalgebren 2
[Bearbeiten]Insgesamt erhält man für  die äquivalente Bedingung:
die äquivalente Bedingung:

Insbesondere gilt für alle 
 .
.
Also gibt es mindestens ein  , sodass für alle
, sodass für alle  gilt:
gilt:
 .
.
Wenn man die  -Singularität betrachtet, gibt es zu jedem
-Singularität betrachtet, gibt es zu jedem  ein
ein  mit
mit  , sodass
, sodass  und es gilt mit der Eigenschaft
und es gilt mit der Eigenschaft  erhält man die Eigenschaft:
erhält man die Eigenschaft:
 .
.
Mit der Eigenschaft  erhält man zunächst einmal die Abschätzung:
erhält man zunächst einmal die Abschätzung:
 .
.
Vergleich zur Charakterisierung der MLC-Singularität
[Bearbeiten]Durch die Negation erhält man, dass es zu jedem  ein
ein  , in dem
, in dem  also kein topologischer Nullteiler ist. Diese Negation liefert nach
also kein topologischer Nullteiler ist. Diese Negation liefert nach
 .
.
Aufgabe - Äquivalenz des Halbnormensystems - TNT
[Bearbeiten]Wir definieren darüber nun ein weiteres Halbnormensystem  aus submultiplikativen Halbnormen wie folgt über die Eigenschaft von
aus submultiplikativen Halbnormen wie folgt über die Eigenschaft von  , kein topologischer Nullteiler zu sein:
, kein topologischer Nullteiler zu sein:

 , wenn
, wenn  und
und  mit
mit  die obige Gleichung
die obige Gleichung  erfüllt. Zeigen Sie, dass
erfüllt. Zeigen Sie, dass  und
und  äquivalente Gaugefunktionalsysteme sind
äquivalente Gaugefunktionalsysteme sind
Sei  eine Indexmenge. In der folgenden Charakterisierung der
eine Indexmenge. In der folgenden Charakterisierung der  -Regularität werden Produkträume definiert bzw. als Algebraerweiterung konstruiert. Dabei wird folgende Kurzschreibweise des Produktraumes
-Regularität werden Produkträume definiert bzw. als Algebraerweiterung konstruiert. Dabei wird folgende Kurzschreibweise des Produktraumes  verwendet.
verwendet.

Beweisidee: Konstruktion der MLC-Algebraerweiterung
[Bearbeiten]Ausgehend von  wird ein Produktraum
wird ein Produktraum  von normierten Algebren
von normierten Algebren  betrachtet und topologisiert. Auf die normierten Algebren wird mit der Eigenschaft
betrachtet und topologisiert. Auf die normierten Algebren wird mit der Eigenschaft  die gesuchte Eigenschaft
die gesuchte Eigenschaft ![{\displaystyle \|\!|[x]_{\alpha }|\!\|_{\alpha }\leq D_{\alpha }\cdot \|\!|[z]_{\alpha }\cdot [x]_{\alpha }|\!\|_{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0193a59aba25c6f73d780323a0990ad84935969) geliefert und auf alle normierten Algebren
geliefert und auf alle normierten Algebren  angewendet, um eine Algebraerweiterung
angewendet, um eine Algebraerweiterung  zu erhalten, in der
zu erhalten, in der ![{\displaystyle [z]_{\alpha }\in A_{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a93ef13c37389d7e4a4c68533fd37b29aa7719b6) invertierbar ist.
invertierbar ist.
Algebraisomorphismus in den Quotientenräumen
[Bearbeiten]Der Algebraisomorphismus wird dann mit
 ,
,
mit ![{\displaystyle \tau _{\alpha }([z]_{\alpha })=z_{\alpha }\in A'_{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa4d3a3ccf641a8abcf2bc76b116c5a91e1653ac) bezeichnet.
bezeichnet.
Algebraerweiterung von MLC-Quotientenalgebren
[Bearbeiten]
Embettung in Quotientenräume bzgl. der submultiplikativen Halbnormen.
Schritt 1: Übergang zu Quotientenräumen
[Bearbeiten]Man betrachtet für jede submultitplikative Halbnorm  das Ideal
das Ideal

Dann definiert man  als Quotientenraum
als Quotientenraum  .
.
Aufgabe: Idealeigenschaften nachweisen
[Bearbeiten]Zeigen Sie, dass  ein Ideal in
ein Ideal in  und
und  eine Algebra.
eine Algebra.
Schritt 2: Topologisierung der Quotientenräume
[Bearbeiten]Man verwendet als Halbnorm auf dem Quotientenraum die  mit
mit
![{\displaystyle \|\!|\,[x]_{\alpha }|\!\|_{\alpha }:=\|\!|\underbrace {x+N_{\alpha }} _{=[x]_{\alpha }}|\!\|_{\alpha }=\displaystyle \inf _{u\in N_{\alpha }}\|x+u\|_{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/deb55d1f493b64f6e8ce6d129546e894e8fe3bf4)
Aufgaben: Submultiplikative Halbnorm im Quotientenraum
[Bearbeiten]Zeigen Sie, dass  eine submultiplikative Norm auf dem Quotientenraum
eine submultiplikative Norm auf dem Quotientenraum  ist und
ist und ![{\displaystyle \|\!|\,[x]_{\alpha }|\!\|_{\alpha }=\|x\|_{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01a7786463dbd80c3b393ee977f9fa61ac4e4e53) gilt.
gilt.
Für die normierten Algebren  nutzt man die Charakterisierung der
nutzt man die Charakterisierung der  -Regularität und erhält Algebraerweiterungen
-Regularität und erhält Algebraerweiterungen  in denen
in denen  das inverse Element
das inverse Element ![{\displaystyle [b_{\alpha }]_{\alpha }\in B_{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc3a2e7b0a651c5175667e189ecfaabebfc195f2) mit dem Algebraisomorphismus der Einbettung
mit dem Algebraisomorphismus der Einbettung  mit einem Inversen Element
mit einem Inversen Element  zu
zu ![{\displaystyle [z]_{\alpha }\in A_{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a93ef13c37389d7e4a4c68533fd37b29aa7719b6) d.h.
d.h.
![{\displaystyle z_{\alpha }\cdot b_{\alpha }=b_{\alpha }\cdot z_{\alpha }=e_{\alpha }=t_{\alpha }(\underbrace {e_{A}+N_{\alpha }} _{[e_{A}]_{\alpha }})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7f83ed37047d9e04342341c6157a418e3e298eb)
Aufgabe: Positivität der Halbnorm für das inverse Element
[Bearbeiten]Zeigen Sie, dass  und
und  für alle
für alle  erfüllt sind, wenn
erfüllt sind, wenn  ist. Nutzen Sie dazu die Eigenschaft, dass das Halbnormensystem
ist. Nutzen Sie dazu die Eigenschaft, dass das Halbnormensystem  unital positiv ist und mit
unital positiv ist und mit  eine Isometrie vorliegt.
eine Isometrie vorliegt.
Aufgabe: Unitale Positivität der Halbnormen und inverse Elemente in Quotientenräumen
[Bearbeiten]Zeigen Sie, dass in einem unital positiven multipliklativen Halbnormensystem  ein Element
ein Element  genau dann in
genau dann in  -regulär ist, wenn es
-regulär ist, wenn es  -regulär in jeder normierten Algebra
-regulär in jeder normierten Algebra  für alle
für alle  ist mit:
ist mit:
![{\displaystyle \|\!|\,[x]_{\alpha }|\!\|_{\alpha }:=\|\!|\underbrace {x+N_{\alpha }} _{=[x]_{\alpha }}|\!\|_{\alpha }=\displaystyle \inf _{u\in N_{\alpha }}\|x+u\|_{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/deb55d1f493b64f6e8ce6d129546e894e8fe3bf4)
Schritt 4: Definition des Algebraisomorphismus
[Bearbeiten]Der Algebraisomorphismus  setzt sich aus zwei verketteten Abbildungen
setzt sich aus zwei verketteten Abbildungen  zusammen mit
zusammen mit ![{\displaystyle {\widehat {A}}:=\{([x]_{\alpha })_{\alpha \in {\mathcal {A}}}\,:\,x\in A\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e71c7d34a0f6d4f09aa1086f8e6552d0317276ce) :
:
 mit
mit ![{\displaystyle \tau _{1}(x)=([x]_{\alpha })_{\alpha \in {\mathcal {A}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9405792c8b8d4507cb76212b4417c52beb9c14a6)
 mit
mit ![{\displaystyle \tau _{2}(x')=\tau _{2}\left(([x]_{\alpha })_{\alpha \in {\mathcal {A}}}\right)=(x_{\alpha })_{\alpha \in {\mathcal {A}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/936a71852ef6cab502673df6638c02562ea463c2)
Aufgabe: Surjektivität und Produktraum
[Bearbeiten]Zeigen Sie zunächst, dass  und
und  Algebraisomorphismen von Algebraerweiterungen sind!
Algebraisomorphismen von Algebraerweiterungen sind!
Aufgabe: Surjektivität und Produktraum
[Bearbeiten]Ersetzt man den Wertebereich ![{\displaystyle {\widehat {A}}:=\{([x]_{\alpha })_{\alpha \in {\mathcal {A}}}\,:\,x\in A\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e71c7d34a0f6d4f09aa1086f8e6552d0317276ce) durch den Produktraum der Quotientenräume
durch den Produktraum der Quotientenräume  , so ist die modifizierte Abbildungen
, so ist die modifizierte Abbildungen  keine Algebraisomorphismen mehr.
Begründen Sie, warum ist
keine Algebraisomorphismen mehr.
Begründen Sie, warum ist  mit geändertem Wertebereich nicht mehr surjektiv ist, wenn
mit geändertem Wertebereich nicht mehr surjektiv ist, wenn  mehr als einen Index enthält?
mehr als einen Index enthält?
Schritt 5: Neutrales Element im Produktraum
[Bearbeiten]Das neutrale im Produktraum erhält man damit über  mit:
mit:
![{\displaystyle \tau (e_{A})=\tau _{2}\left(([e_{A}]_{\alpha })_{\alpha \in {\mathcal {A}}}\right)=\tau _{2}\left((e_{A}+N_{\alpha })_{\alpha \in {\mathcal {A}}}\right)=(e_{\alpha })_{\alpha \in {\mathcal {A}}}=:e_{B}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41766e8ce46525bb126fe87019e81d23c06773a8) .
.
Die Invertierbarkeit im Produktraum  erhält man über
erhält man über
 .
.
Bermerkung: Notation der Elemente in der Algebraerweiterung
[Bearbeiten]Man muss bei der Notation in der Algebraerweiterung folgenden Notationen unterscheiden:

![{\displaystyle ([z]_{\alpha })_{\alpha \in {\mathcal {A}}}=(z+N_{\alpha })_{\alpha \in {\mathcal {A}}}\in (A_{\alpha })_{\alpha \in {\mathcal {A}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a96880772e62a613ec3beaa27ae44f61de3a98cf) mit
mit 
In der zweiten Schreibweise gibt es in jeder Komponente  des Produktraumes
des Produktraumes  den gleichen Repräsentanten
den gleichen Repräsentanten  , während in der ersten Schreibweise für die Notation des Inversen die Repräsentanten
, während in der ersten Schreibweise für die Notation des Inversen die Repräsentanten  für jedes
für jedes  unterschiedlich sein können.
unterschiedlich sein können.
Nach Konstruktion der Algebraerweiterung der normierten Algebra  Algebraerweiterungen auf
Algebraerweiterungen auf  nach der Charakterisierung der
nach der Charakterisierung der  -Regularität ist die Algebraerweiterung eine Isometrie, d.h. für alle
-Regularität ist die Algebraerweiterung eine Isometrie, d.h. für alle  gilt für alle
gilt für alle  :
:
![{\displaystyle \|\!|\,([x_{\alpha }]_{\alpha })_{\alpha _{0}\in {\mathcal {A}}}\,|\!\|_{\alpha }=\|\!|\tau _{2}\left(\,([x_{\alpha }]_{\alpha })_{\alpha \in {\mathcal {A}}}\,\right)|\!\|_{B_{\alpha _{0}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8744b4ecc2a1818e4eb22379769b796b121bd039)
Schritt 6: Topologisierung der Algebraerweiterung
[Bearbeiten]Für alle  definiert man mit
definiert man mit ![{\displaystyle \tau (x)=([x]_{\alpha })_{\alpha \in {\mathcal {A}}}\in (B_{\alpha })_{\alpha \in {\mathcal {A}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d5608512b7b0daabc39916b3f32699ef24a2117) und für
und für ![{\displaystyle {\widehat {b\,}}:=([{\widehat {b\,}}_{\alpha }]_{\alpha \in {\widetilde {A}}}\in B}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc61c04fafc2c3fe6bfe5dc9edf5b7866618c8cf) setzt man
setzt man
![{\displaystyle \|{\widehat {b\,}}\|_{\alpha _{o}}:=\|\,([{\widehat {b\,}}_{\alpha }])_{\alpha \in {\mathcal {A}}}\|_{\alpha _{o}}:=\|\!|\,[{\widehat {b\,}}_{\alpha _{o}}]_{\alpha _{o}}|\!\|_{\alpha _{o}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7d9f5cc8317be32c417dc9b8ec81a1d619f8772) .
.
Aufgabe: Zeigen Sie, dass der Algebraisomorphismus  eine Isometrie ist, d.h.
eine Isometrie ist, d.h.

Schritt 7: Inverses Element in der Algebraerweiterung
[Bearbeiten]Das inverse Element von  ist dann in
ist dann in  mit einem inversen Element
mit einem inversen Element  , das komponentenweise als
, das komponentenweise als  definiert wird mit
definiert wird mit  für alle
für alle  .
.
Die Vollständigkeit, die für die B-Regularität noch betrachtet wurde, spielt hier für die  -Regularität keine Rolle, da nur das Vorgehen für Konstruktion einer Algebraerweiterung zu einer normierten Algebra
-Regularität keine Rolle, da nur das Vorgehen für Konstruktion einer Algebraerweiterung zu einer normierten Algebra  benötigt wird.
benötigt wird.
Der Beweis der Charakterisierung  -Regularität wurde von Zelazko bereits 1971 gezeigt[1] als Charakterisierung der permant singulären Elemente von
-Regularität wurde von Zelazko bereits 1971 gezeigt[1] als Charakterisierung der permant singulären Elemente von  -Algebren.
-Algebren.
Der Nachweis der Charakterisierung der  -Regularität ist ein Spezialfall der
-Regularität ist ein Spezialfall der  -Regularität für multplikative pseudokonvexe Räume, wobei die
-Regularität für multplikative pseudokonvexe Räume, wobei die  -Normen mit
-Normen mit  homogen sind und damit die Eigenschaften einer Norm erfüllt.
homogen sind und damit die Eigenschaften einer Norm erfüllt.
Bei der  -Regularität wurde die Algebraerweiterung
-Regularität wurde die Algebraerweiterung  über die
über die  -Regularität, die Definition von isometrischen Algebraisomorphismen und der Betrachtung von Quotientenräume konstruktiert, in der ein
-Regularität, die Definition von isometrischen Algebraisomorphismen und der Betrachtung von Quotientenräume konstruktiert, in der ein  invertierbar ist.
invertierbar ist.
Direkte Konstruktion der Algebraerweiterung
[Bearbeiten]Eine direkte Konstruktion der Algebraerweiterung über die topologische Eigenschaften von  ist für
ist für  -Regularität ebenfalls möglich. Dabei wird wieder die Polynomalgebra
-Regularität ebenfalls möglich. Dabei wird wieder die Polynomalgebra ![{\displaystyle A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13daf73f25e64310e7e5d67c5aa8dd4f97cb884f) topologisiert und dann der Quotientenraum
topologisiert und dann der Quotientenraum ![{\displaystyle A[t]/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1292ce6570ccc7cfbb0fb322431e6a335332c441) betrachtet, wobei dann
betrachtet, wobei dann  das Hauptideal
das Hauptideal ![{\displaystyle I:=o\cdot A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a1c9cd3681d946591cd8913c805b574013e3ed1) ist und
ist und  ein Repräsentant des Nullvektors
ein Repräsentant des Nullvektors  in der Algebraerweiterung
in der Algebraerweiterung ![{\displaystyle B=A[t]/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03d477a159f54a52cd2287686a57f356696cf4bf) ist. Der direkte Beweis wird bei der Charakterisierung der
ist. Der direkte Beweis wird bei der Charakterisierung der  -Regularität geführt und kann mit
-Regularität geführt und kann mit  auf
auf  -Regularität übertragen werden.
-Regularität übertragen werden.
- ↑ a b Zelazko Wieslaw, On permanently singular elements in commutative m-convex locally convex algebras, Studia Math. 37 (1971), S. 181-190
Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.
Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Topologische Invertierbarkeitskriterien' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.










































![{\displaystyle \tau _{\alpha }(x)=[x]_{\alpha }\in A'_{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c79230820ee51cceb0d1ab03aad2f6cfabadeafa)




![{\displaystyle B:=A[t]/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bc806fa49af6a80a0b8ba7a4eb54a8d503dd8ab)




















































![{\displaystyle \|\!|[x]_{\alpha }|\!\|_{\alpha }\leq D_{\alpha }\cdot \|\!|[z]_{\alpha }\cdot [x]_{\alpha }|\!\|_{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0193a59aba25c6f73d780323a0990ad84935969)

![{\displaystyle [z]_{\alpha }\in A_{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a93ef13c37389d7e4a4c68533fd37b29aa7719b6)
![{\displaystyle \tau _{\alpha }([z]_{\alpha })=z_{\alpha }\in A'_{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa4d3a3ccf641a8abcf2bc76b116c5a91e1653ac)




![{\displaystyle \|\!|\,[x]_{\alpha }|\!\|_{\alpha }:=\|\!|\underbrace {x+N_{\alpha }} _{=[x]_{\alpha }}|\!\|_{\alpha }=\displaystyle \inf _{u\in N_{\alpha }}\|x+u\|_{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/deb55d1f493b64f6e8ce6d129546e894e8fe3bf4)
![{\displaystyle \|\!|\,[x]_{\alpha }|\!\|_{\alpha }=\|x\|_{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01a7786463dbd80c3b393ee977f9fa61ac4e4e53)

![{\displaystyle [b_{\alpha }]_{\alpha }\in B_{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc3a2e7b0a651c5175667e189ecfaabebfc195f2)

![{\displaystyle z_{\alpha }\cdot b_{\alpha }=b_{\alpha }\cdot z_{\alpha }=e_{\alpha }=t_{\alpha }(\underbrace {e_{A}+N_{\alpha }} _{[e_{A}]_{\alpha }})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7f83ed37047d9e04342341c6157a418e3e298eb)






![{\displaystyle {\widehat {A}}:=\{([x]_{\alpha })_{\alpha \in {\mathcal {A}}}\,:\,x\in A\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e71c7d34a0f6d4f09aa1086f8e6552d0317276ce)

![{\displaystyle \tau _{1}(x)=([x]_{\alpha })_{\alpha \in {\mathcal {A}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9405792c8b8d4507cb76212b4417c52beb9c14a6)

![{\displaystyle \tau _{2}(x')=\tau _{2}\left(([x]_{\alpha })_{\alpha \in {\mathcal {A}}}\right)=(x_{\alpha })_{\alpha \in {\mathcal {A}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/936a71852ef6cab502673df6638c02562ea463c2)







![{\displaystyle \tau (e_{A})=\tau _{2}\left(([e_{A}]_{\alpha })_{\alpha \in {\mathcal {A}}}\right)=\tau _{2}\left((e_{A}+N_{\alpha })_{\alpha \in {\mathcal {A}}}\right)=(e_{\alpha })_{\alpha \in {\mathcal {A}}}=:e_{B}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41766e8ce46525bb126fe87019e81d23c06773a8)



![{\displaystyle ([z]_{\alpha })_{\alpha \in {\mathcal {A}}}=(z+N_{\alpha })_{\alpha \in {\mathcal {A}}}\in (A_{\alpha })_{\alpha \in {\mathcal {A}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a96880772e62a613ec3beaa27ae44f61de3a98cf)


![{\displaystyle \|\!|\,([x_{\alpha }]_{\alpha })_{\alpha _{0}\in {\mathcal {A}}}\,|\!\|_{\alpha }=\|\!|\tau _{2}\left(\,([x_{\alpha }]_{\alpha })_{\alpha \in {\mathcal {A}}}\,\right)|\!\|_{B_{\alpha _{0}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8744b4ecc2a1818e4eb22379769b796b121bd039)
![{\displaystyle \tau (x)=([x]_{\alpha })_{\alpha \in {\mathcal {A}}}\in (B_{\alpha })_{\alpha \in {\mathcal {A}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d5608512b7b0daabc39916b3f32699ef24a2117)
![{\displaystyle {\widehat {b\,}}:=([{\widehat {b\,}}_{\alpha }]_{\alpha \in {\widetilde {A}}}\in B}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc61c04fafc2c3fe6bfe5dc9edf5b7866618c8cf)
![{\displaystyle \|{\widehat {b\,}}\|_{\alpha _{o}}:=\|\,([{\widehat {b\,}}_{\alpha }])_{\alpha \in {\mathcal {A}}}\|_{\alpha _{o}}:=\|\!|\,[{\widehat {b\,}}_{\alpha _{o}}]_{\alpha _{o}}|\!\|_{\alpha _{o}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7d9f5cc8317be32c417dc9b8ec81a1d619f8772)








![{\displaystyle A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13daf73f25e64310e7e5d67c5aa8dd4f97cb884f)
![{\displaystyle A[t]/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1292ce6570ccc7cfbb0fb322431e6a335332c441)

![{\displaystyle I:=o\cdot A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a1c9cd3681d946591cd8913c805b574013e3ed1)


![{\displaystyle B=A[t]/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03d477a159f54a52cd2287686a57f356696cf4bf)