Bei der Cauchy-Multiplkikation hat man im allgemeinen Fall eine topologischen Algebra nicht mehr die Dreieckungleichung einer Halbnorm oder die Abschätzung mit einer Stetigkeitskonstante der Addition mit einer Quasinorm zur Verfügung und man muss bei der Addition für die Stetigkeit gegen ein anderen  -Gaugefunktional abschätzen.
-Gaugefunktional abschätzen.

Dies führt zur Betrachtung von kaskadierenden Summen, die für die Abschätzung der Cauchy-Multimultiplikation auf der Polynomalgebra ![{\displaystyle A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13daf73f25e64310e7e5d67c5aa8dd4f97cb884f) verwendet wird.
verwendet wird.
Die Stetigkeit des Cauchy-Produktes ist wesentlich für den ersten Schritt der Erweiterung auf die Algebra der Polynome.
Kaskaden bei Brunnen sind namensgebend für die kaskadierende Summen von Gaugefunktionalen (siehe folgende Abbildungen)

Kaskadierende Summe mit Gaugefunktionalen
[Bearbeiten]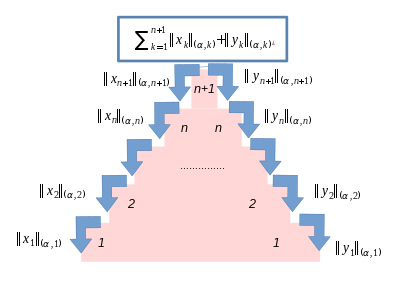
Kaskadenabschätzung für das Cauchy-Produkt
[Bearbeiten]Betrachtet man in Polynomalgebren ![{\displaystyle A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13daf73f25e64310e7e5d67c5aa8dd4f97cb884f) das Cauchy-Produkt, dann muss man die Polynomalgebra in einer Weise topologisieren, dass die Verknüpfungen auf der Algebra (also insbesondere die Multiplikation von Polynomen stetig sind. In allgemeinen topologischen Algebren gibt es keine Dreieckungleichung und daher erhöht sich bei Anwendung der Subadditivität bzw. Submultiplikativität jeweils der Index in der Sequenz. Nun ist es das Ziel die Lemma über Kaskadensummen und Kaskadenprodukte für die Stetigkeit der Cauchymultiplkation nutzbar zu machen.
das Cauchy-Produkt, dann muss man die Polynomalgebra in einer Weise topologisieren, dass die Verknüpfungen auf der Algebra (also insbesondere die Multiplikation von Polynomen stetig sind. In allgemeinen topologischen Algebren gibt es keine Dreieckungleichung und daher erhöht sich bei Anwendung der Subadditivität bzw. Submultiplikativität jeweils der Index in der Sequenz. Nun ist es das Ziel die Lemma über Kaskadensummen und Kaskadenprodukte für die Stetigkeit der Cauchymultiplkation nutzbar zu machen.
Gegeben sind allgemein zwei Polynome  mit Koeffizienten aus
mit Koeffizienten aus  .
.

Dann wird Cauchy-Produkt von  wie folgt definiert:
wie folgt definiert:

Gaugefunktional aus Stetigkeitssequenzen
[Bearbeiten]Betrachtet man zwei Polynome ![{\displaystyle p,q\in A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c1a2e0a3e71f7b320f81e4090bb53df3fd3ce9d) in einer topologischen Algebra
in einer topologischen Algebra ![{\displaystyle (A[t],\|\!|\cdot |\!\|_{\mathcal {A}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce37a3f21b3061f5ff6c81bd2bf9b4efc318475a) .
.

Dann liefert die Definition des  -Gaugefunktionals für das Produkt
-Gaugefunktionals für das Produkt  :
:

Bemerkung - Koeffizienten in Gaugefunktionalen
[Bearbeiten]Für die Regularitätbeweise erhalten die Gaugefunktional auf der Polynomalgebra ![{\displaystyle A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13daf73f25e64310e7e5d67c5aa8dd4f97cb884f) noch positive Konstanten als Vorfaktoren.
noch positive Konstanten als Vorfaktoren.

Bei den folgenden Vorüberlegungen entfallen diese zunächst, um das Vorgehen bzgl. der Kaskadenabschätzung zu klären.
Für eine Cauchy-Produkt in der Polynomagebra ![{\displaystyle A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13daf73f25e64310e7e5d67c5aa8dd4f97cb884f) kann man zu jedem
kann man zu jedem  eine Stetigkeitssequenz
eine Stetigkeitssequenz  finden, die die folgende Ungleichung erfüllt.
finden, die die folgende Ungleichung erfüllt.

Bei einem Cauchy-Produkt auf der Polynomalgebra greifen additive Verknüpfungen von  Summanden mit einer multiplikativen Verknüpfung von zwei Koeffizienten inneinander. Bei der Addition hat man im allgemeinen Fall einer topologischen Algebra nicht mehr auf die Dreiecksungleichung bzw. die Subadditivität mit Stetigkeitskonstante einer Quasihalbnorm zurückgreifen. Als Ersatz wird das Kaskadenlemma der Addition verwendet, um auch auf der Polynomalgebra stetige algebraische Verknüpfungen für die Algebraerweiterung zu erhalten.
Summanden mit einer multiplikativen Verknüpfung von zwei Koeffizienten inneinander. Bei der Addition hat man im allgemeinen Fall einer topologischen Algebra nicht mehr auf die Dreiecksungleichung bzw. die Subadditivität mit Stetigkeitskonstante einer Quasihalbnorm zurückgreifen. Als Ersatz wird das Kaskadenlemma der Addition verwendet, um auch auf der Polynomalgebra stetige algebraische Verknüpfungen für die Algebraerweiterung zu erhalten.
Anwendung des Kaskadenlemmas für Summen
[Bearbeiten]Fallunterscheidung für  gerade bzw. ungerade. In Abhängigkeit von der Anzahl der Summanden werden die
gerade bzw. ungerade. In Abhängigkeit von der Anzahl der Summanden werden die  und
und  im Kaskadenlemma für Summen definiert.
im Kaskadenlemma für Summen definiert.
 ist ein Koeffizient von
ist ein Koeffizient von  , wobei sich
, wobei sich  zerlegen lässt.
zerlegen lässt. ist ein Koeffizient von
ist ein Koeffizient von  , wobei sich
, wobei sich  zerlegen lässt.
zerlegen lässt.
Kaskadenlemma - ungerade Anzahl Summanden
[Bearbeiten]Ist  ungerade definiert man
ungerade definiert man
 und
und 
Ist  ungerade definiert man
ungerade definiert man
 und
und 
 und
und 
Dies Vorgehen wird nun allgemein für beliebige ungerade  verwendet.
verwendet.
Anwendung Kaskadenlemma 1 - ungerade Anzahl Summanden
[Bearbeiten]Durch Anwendung auf das Cauchy-Produkt erhält man mit Indexverschiebung und  :
:

Stetigkeit Multiplikation 2 - ungerade Anzahl Summanden
[Bearbeiten]Durch Anwendung Korollar - Kaskadensummen auf das Cauchy-Produkt erhält man Indexverschiebung:

Abschätzung Laufindex 3 - ungerade Anzahl Summanden
[Bearbeiten]Mit  und
und  ungerade gilt:
ungerade gilt:
- Aus
 folgt
folgt  und
und
- Insgesamt

Notwendig für Isotonie der Gaugefunktionale

Isotonie Sequenz 4 - ungerade Anzahl Summanden
[Bearbeiten]Durch Anwendung der Isotonie auf das Produkt erhält man mit  :
:

Cauchyprodukt 5 - ungerade Anzahl Summanden
[Bearbeiten]Durch geeignet Umsortierung der Summanden erhält man mit  :
:

Kaskadenlemma - gerade Anzahl Summanden
[Bearbeiten]Ist  gerade, definiert man
gerade, definiert man
 und
und 
 und
und 
Ist  gerade definiert man
gerade definiert man
 und
und 
 und
und 
 und
und 
Dies Vorgehen wird nun allgemein für beliebige gerade  verwendet.
verwendet.
Anwendung Kaskadenlemma 1 - gerade Anzahl Summanden
[Bearbeiten]Durch Anwendung auf das Cauchy-Produkt erhält man mit  und
und  :
:

Stetigkeit Multiplikation 2 - gerade Anzahl Summanden
[Bearbeiten]Durch Anwendung Korollar - Kaskadensummen und isotonie erhält mit  :
:

Abschätzung Laufindex 3 - gerade Anzahl Summanden
[Bearbeiten]Mit  und
und  gerade gilt:
gerade gilt:
- Aus
 folgt
folgt  und
und
- Insgesamt

Notwendig für Isotonie der Gaugefunktionale

Isotonie Sequenz 4 - gerade Anzahl Summanden
[Bearbeiten]Durch Anwendung auf der Isotonie auf das Produkt erhält:

Cauchyprodukt 5 - gerade Anzahl Summanden
[Bearbeiten]Durch geeignete Umsortierung der Summanden erhält man mit  und
und  :
:

Insgesamt erhält man

Koeffizienten im Gaugefunktional - Polynomalgebra
[Bearbeiten]Mit den obigen Vorüberlegungen ist das prinzipielle Vorgehen für die Cauchy-Multiplikation geklärt. Nun fehlt noch die Integration der Koeffzienten, die durch die Konstanten aus dem  -Regularitätkriterium für die Gaugefunktionale auf
-Regularitätkriterium für die Gaugefunktionale auf ![{\displaystyle A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13daf73f25e64310e7e5d67c5aa8dd4f97cb884f) berücksichtigt werden müssen.
berücksichtigt werden müssen.
Stetigkeitssequenzen auf Polynomalgebren
[Bearbeiten]Wir betrachten nun Stetigkeitssequenzen von Gaugefunktionalen auf Polynomalgebren in ![{\displaystyle q\in A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8d24715a3c26d1fa7abd1b832d7df621423b120) in einer topologischen Algebra
in einer topologischen Algebra ![{\displaystyle (A[t],\|\!|\cdot |\!\|_{{\mathcal {A}}\times \mathbb {N} _{0}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/247aebaa6265634ab723b28589dcdf2361045ed1) .
.

Dabei muss man in einem nächsten Schritt die Koeffizienten  so definieren, dass man wie bei den anderen Regularitätsbeweisen mit
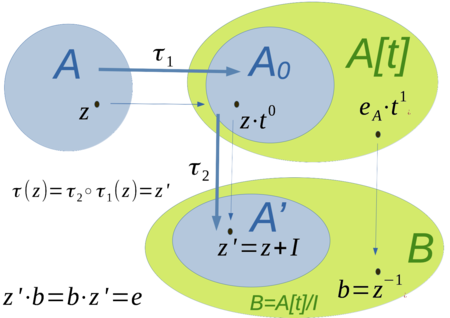
so definieren, dass man wie bei den anderen Regularitätsbeweisen mit ![{\displaystyle B:=A[t]/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bc806fa49af6a80a0b8ba7a4eb54a8d503dd8ab) Algebraerweiterung von
Algebraerweiterung von  erhält in der
erhält in der  invertierbar ist.
invertierbar ist.
Sei  eine topologische Algebra mit dem basiserzeugenden Gaugefunktionalsystem
eine topologische Algebra mit dem basiserzeugenden Gaugefunktionalsystem  . Da
. Da  die Hausdorff-Eigenschaft besitzt, trennt
die Hausdorff-Eigenschaft besitzt, trennt  die Punkte, d.h. gilt für alle
die Punkte, d.h. gilt für alle  mit
mit  gibt ein
gibt ein  , sodass man mit
, sodass man mit  den "Unterschied messen" kann und
den "Unterschied messen" kann und  gilt.
gilt.
Hausdorff-Eigenschaft - Polynomalgebra
[Bearbeiten]Damit auch die Polynomalgebra ![{\displaystyle A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13daf73f25e64310e7e5d67c5aa8dd4f97cb884f) die Hausdorff-Eigenschaft besitzt, definitiert man
die Hausdorff-Eigenschaft besitzt, definitiert man  und
und  mit
mit

Aufgabe für Studierende - Polynomalgebra
[Bearbeiten]Sei ![{\displaystyle (A[t],\|\!\|\cdot \|\!\|_{{\mathcal {A}}\times \mathbb {N} _{0}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0357b4ab6b4f7a720f084cff056b92f9fbd375fa) eine Polynomalgebra mit Koeffizienten aus der topologische Algebra
eine Polynomalgebra mit Koeffizienten aus der topologische Algebra  und einem basiserzeugenden Gaugefunktionalsystem
und einem basiserzeugenden Gaugefunktionalsystem  auf
auf  , wie oben definiert.
, wie oben definiert.
Hausdorff-Eigenschaft - Polynomalgebra
[Bearbeiten]Zeigen Sie, dass die Polynomalgebra ![{\displaystyle (A[t],\|\!\|\cdot \|\!\|_{{\mathcal {A}}\times \mathbb {N} _{0}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0357b4ab6b4f7a720f084cff056b92f9fbd375fa) ein Hausdorff-Raum ist.
ein Hausdorff-Raum ist.
Stetigkeit der Addition - Polynomalgebra
[Bearbeiten]Zeigen Sie, dass in der Polynomalgebra ![{\displaystyle (A[t],\|\!\|\cdot \|\!\|_{{\mathcal {A}}\times \mathbb {N} _{0}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0357b4ab6b4f7a720f084cff056b92f9fbd375fa) die Addition stetig ist.
die Addition stetig ist.
Stetigkeit der Multiplikation - Polynomalgebra
[Bearbeiten]Zeigen Sie, dass in der Polynomalgebra ![{\displaystyle (A[t],\|\!\|\cdot \|\!\|_{{\mathcal {A}}\times \mathbb {N} _{0}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0357b4ab6b4f7a720f084cff056b92f9fbd375fa) die Multiplikation stetig ist.
die Multiplikation stetig ist.
Homogenität der Multiplikation mit Skalaren - Polynomalgebra
[Bearbeiten]Zeigen Sie, dass in der Polynomalgebra ![{\displaystyle (A[t],\|\!\|\cdot \|\!\|_{{\mathcal {A}}\times \mathbb {N} _{0}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0357b4ab6b4f7a720f084cff056b92f9fbd375fa) die Gaugefunktionale
die Gaugefunktionale  die homogen sind und damit Multiplikation mit Skalaren auf
die homogen sind und damit Multiplikation mit Skalaren auf ![{\displaystyle A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13daf73f25e64310e7e5d67c5aa8dd4f97cb884f) stetig ist (siehe Topologisierungslemma für Algebren).
stetig ist (siehe Topologisierungslemma für Algebren).
Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.
Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Topologische Invertierbarkeitskriterien' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.



![{\displaystyle A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13daf73f25e64310e7e5d67c5aa8dd4f97cb884f)







![{\displaystyle p,q\in A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c1a2e0a3e71f7b320f81e4090bb53df3fd3ce9d)
![{\displaystyle (A[t],\|\!|\cdot |\!\|_{\mathcal {A}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce37a3f21b3061f5ff6c81bd2bf9b4efc318475a)




















































![{\displaystyle q\in A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8d24715a3c26d1fa7abd1b832d7df621423b120)
![{\displaystyle (A[t],\|\!|\cdot |\!\|_{{\mathcal {A}}\times \mathbb {N} _{0}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/247aebaa6265634ab723b28589dcdf2361045ed1)


![{\displaystyle B:=A[t]/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bc806fa49af6a80a0b8ba7a4eb54a8d503dd8ab)











![{\displaystyle (A[t],\|\!\|\cdot \|\!\|_{{\mathcal {A}}\times \mathbb {N} _{0}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0357b4ab6b4f7a720f084cff056b92f9fbd375fa)
