Äquivalenzrelation/Quotientenmenge/2/Textabschnitt
Es sei eine Äquivalenzrelation und die Quotientenmenge. Die Abbildung
heißt kanonische Projektion von .
Mit Hilfe der Quotientenmenge werden die Äquivalenzklassen zu Elementen einer neuen Menge gemacht. Durch die kanonische Projektion werden äquivalente Elemente miteinander identifiziert. Man spricht daher bei Äquivalenzrelationen auch von der Kunst des Identifizierens. Im praktischen Umgang mit den Quotientenmengen tritt häufig die eigentliche Definition in den Hintergrund und man arbeitet eher mit den intrinsischen Eigenschaften dieser Mengen. Die folgende Aussage besagt insbesondere, dass man jede Äquivalenzrelation wie in Beispiel erhalten kann. Äquivalent bedeutet also stets gleich unter einer geeigneten Abbildung.
Es sei eine Menge und eine Äquivalenzrelation auf mit den Äquivalenzklassen und der Quotientenmenge . Dann gelten folgende Aussagen.
- Es ist genau dann, wenn ist, und dies gilt genau dann, wenn .
- ist eine disjunkte Vereinigung.
- Die
kanonische Projektion
ist surjektiv.
- Es ist .
- Es sei eine Abbildung mit für alle mit . Dann gibt es eine eindeutig bestimmte Abbildung mit .
- Es seien und äquivalent und . Dann ist und nach der Transitivität auch , also . Damit stimmen die Äquivalenzklassen überein. Die Implikation von der Mitte nach rechts ist klar, da wegen Äquivalenzklassen nicht leer sind. Es sei nun , und sei ein Element im Durchschnitt. Dann ist und und wegen der Transitivität ist .
- Wegen der Reflexivität ist und daher ist . Wegen Teil (1) ist die Vereinigung disjunkt.
- Die Surjektivität ist klar aufgrund der Definition der Quotientenmenge, und da auf die Klasse geschickt wird.
- Es ist
- Sei gegeben. Die einzige Möglichkeit für ist zu setzen. Es muss aber gezeigt werden, dass diese Abbildung überhaupt wohldefiniert ist, also unabhängig von der Wahl des Repräsentanten ist. Es sei hierzu , also . Dann ist nach der Voraussetzung an aber .
Wesentliche mathematische Konstruktionen beschreibt man mit Hilfe von Quotientenmengen bezüglich gewisser Äquivalenzrelationen auf einfacheren Mengen. Dafür geben wir zwei Beispiele.
Es sei und . Der ist ein reeller Vektorraum, wobei die Skalarmultiplikation von und mit bezeichnet wird. Es sei weiter
Zwei Punkte werden also als äquivalent erklärt, wenn sie durch Skalarmultiplikation mit einem Skalar ineinander überführt werden können. Ebenso könnte man sagen, dass zwei Punkte als äquivalent gelten, wenn sie dieselbe Gerade durch den Nullpunkt definieren.
Dass wirklich eine Äquivalenzrelation vorliegt, sieht man so. Die Reflexivität folgt aus für jedes . Zur Symmetrie sei , d.h. es gibt ein mit . Dann gilt aber auch , da ja ein Inverses besitzt. Zum Nachweis der Transitivität sei und angenommen, d.h. es gibt mit und . Dann ist insgesamt mit . Die Äquivalenzklassen zu dieser Äquivalenzrelation sind die einzelnen Geraden durch den Nullpunkt (aber ohne den Nullpunkt). Die Quotientenmenge heißt reell-projektiver Raum (der reellen Dimension ) und wird mit bezeichnet.
Es sei die Menge der natürlichen Zahlen und die Produktmenge mit der komponentenweisen Addition.[1] Wir erklären auf eine Relation durch
Dies ist bei genau dann der Fall, wenn es ein (nämlich ) mit
gibt. D.h. die beiden Paare unterscheiden sich um ein Diagonalelement, also um ein Paar, wo beide Komponenten übereinstimmen. Diese Relation ist eine Äquivalenzrelation auf , siehe Aufgabe. Wenn man als ein quadratisches Gitter anordnet (das ist ein „diskretes Koordinatensystem“), so sind die Äquivalenzklassen durch die Punkte auf einer zur Diagonalen parallelen „diskreten Geraden“ gegeben. Die Punkte mit sind äquivalent zu , sie haben also einen Repräsentanten, bei dem die zweite Komponente ist. Die Punkte mit sind äquivalent zu , sie haben also einen Repräsentanten, bei dem die erste Komponente ist. Die Punkte sind zu äquivalent. Den Repräsentanten einer Äquivalenzklasse, bei dem mindestens eine Komponente ist, nennen wir den Standardvertreter dieser Äquivalenzklasse. Die Standardvertreter sind die diskreten Punkte des begrenzenden Viertelkreuzes; zu einem Punkt ergibt sich der Standardvertreter, wenn man parallel zur Diagonalen in Richtung der Halbachsen wandert, bis man auf einer der Halbachsen landet. Zwei Punkte sind genau dann äquivalent, wenn sie den gleichen Standardvertreter besitzen.
Wir bezeichnen nun die Quotientenmenge, also die Menge der Äquivalenzklassen unter dieser Äquivalenzrelation, als Menge der ganzen Zahlen und bezeichnen sie mit . Jede ganze Zahl hat dann genau einen Standardvertreter der Form mit , der Form oder der Form mit . Eine natürliche Zahl fassen wir von nun an als die ganze Zahl auf.
Wir wollen nun zwei ganze Zahlen, also zwei solche Äquivalenzklassen und miteinander „addieren“, also eine Verknüpfung auf einführen. Der naheliegende Ansatz ist, diese Verknüpfung mittels der komponentenweisen Addition als
zu definieren. Hier tritt das Problem der Wohldefiniertheit auf, denn die Verknüpfung wird erklärt unter Bezug auf Repräsentanten, und es ist nicht von vornherein klar, dass unterschiedliche Repräsentanten zum gleichen Ergebnis führen. Wenn also und sind, so muss man überprüfen, dass
und damit ist. Dies ist der Fall, siehe Aufgabe. Man kann weiterhin zeigen, dass die so definierte Verknüpfung auf assoziativ und kommutativ ist, dass das neutrale Element der Verknüpfung ist und dass es zu jedem Element ein inverses Element gibt, nämlich .
Wir definieren nun eine Multiplikation auf durch
Dies ist wieder wohldefiniert und man kann zeigen, dass die Multiplikation assoziativ und kommutativ ist mit als neutralem Element und dass das Distributivgesetz gilt.
- ↑ Passende Interpretationen für die Paare in diesem Kontext sind beispielsweise: Das Paar repräsentiert das Ergebnis eines Fußballspieles, wobei die Toranzahl der Heimmannschaft und die Toranzahl der Gastmannschaft repräsentiert, oder: Das Paar repräsentiert das Alter eines menschlichen Paares, wobei für das Alter der Frau und für das Alter des Mannes steht. Der Übergang zu den Äquivalenzklassen bedeutet dann, sich nur noch für die Tordifferenz bzw. den Altersunterschied zu interessieren, nicht mehr für das genaue Ergebnis bzw. das Alter der einzelnen Personen. Man kann auch das Paar als eine Schrittfolge aus Schritten nach rechts und Schritten nach links ansehen.


![{\displaystyle {}M/R:={\left\{[x]\mid x\in M\right\}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4b3a6e37ac167c6a75d7f64b88ea1a6cc24e311)


![{\displaystyle q_{R}\colon M\longrightarrow M/R,\,x\longmapsto [x],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7c96edb2a455ac421608e115251cbbff46ee269)


![{\displaystyle {}[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c77e93ebf488c686ab4b8693c04bdaae7e8446c)


![{\displaystyle {}[x]=[y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0e31c58238c766c691394b82eb0fc87a5ee0e3f)
![{\displaystyle {}[x]\cap [y]\neq \emptyset }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8deabd43cb75143b1c1b9f06f0e36376615fbc8)
![{\displaystyle {}M=\bigcup _{[x]\in M/\sim }[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9668500885987f8eed93223ae4a06593789272d8)
![{\displaystyle q\colon M\longrightarrow M/\sim ,\,x\longmapsto [x],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93aad292fedc3d5bea8bf5fda10c02c2fc88b15e)
![{\displaystyle {}q^{-1}([x])=[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bb173ce09d3ad591f00a1f6c6c00b0302da17c8)







![{\displaystyle {}u\in [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6a3f679c1338ecdd74dc980755d70d94a834c4d)


![{\displaystyle {}u\in [y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1404b09959e7352fd4601892564498fe1e85d25)




![{\displaystyle {}x\in [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e12337a925c460804120489ba31028dd0fadeff)
![{\displaystyle {}q^{-1}([x])={\left\{y\in M\mid q(y)=[x]\right\}}={\left\{y\in M\mid [y]=[x]\right\}}={\left\{y\in M\mid y\sim x\right\}}=[x]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c95990773ef939c753fe33657ee8f74781384c2)
![{\displaystyle {}[x]\in M/\sim }](https://wikimedia.org/api/rest_v1/media/math/render/svg/09e6ad8b0762f878552d79a7992d41aa87c8949d)

![{\displaystyle {}{\overline {\varphi }}([x]):=\varphi (x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0aeb51915bc1025ad46445ad1264769ddafe76c2)























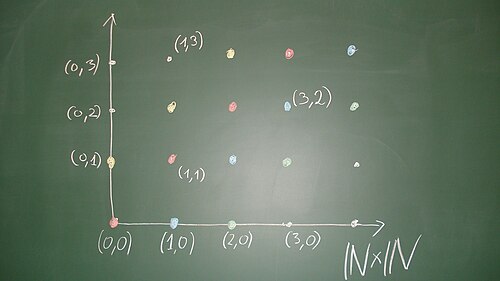






















![{\displaystyle {}[(a,b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad856e5411d0b9ea10ddb04a48932aef19892e7a)
![{\displaystyle {}[(c,d)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b865712c6f9654641f6315839d7fb250d5ed6fa1)

![{\displaystyle {}[(a,b)]\oplus [(c,d)]:=[(a+c,b+d)]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a778629177dd8a896f6ce8cb000f41b321dc395)



![{\displaystyle {}[(a+c,b+d)]=[(a'+c',b'+d')]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b9bc368eabf53b7c89081c97a70ea09b665f4fb)
![{\displaystyle {}[(0,0)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/475a6889495e16a90a7bddd389ad803ee5e078f9)
![{\displaystyle {}[(b,a)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7257885d4524a38fea17a5ad720d33f256cdeaf8)
![{\displaystyle {}[(a,b)]\cdot [(c,d)]:=[(ac+bd,ad+bc)]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e886953fa3c1d350ffa773ec3c5eee3948d2a80c)
![{\displaystyle {}1=[(1,0)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7def7a0131953ef73e591cb841fb440c9b19b53b)

