Kurs:Mathematische Modellbildung/Themen/Modellierung Fleischkonsum
Modellierungsziel
[Bearbeiten]Einleitung
[Bearbeiten]In den vergangenen zwei Jahrzehnten hat sich der weltweite Fleischkonsum aufgrund mehrerer Faktoren, wie zum Beispiel der wachsenden Bevölkerung, mehr als verdoppelt. Auch in Deutschland liegt dieser weit über dem internationalen Durschnitt und gilt als einer der weltweit höchsten. Ein so hoher Konsum hat drastische Auswirkungen auf unsere Umwelt. Immer mehr Tiere werden auf engerem Raum gehalten und riesige Mengen an Weideflächen benötigt. Dadurch steigt auch der deutsche CO2-Ausstoß drastisch und der Klimawandel wird beschleunigt. Außerdem benötigt Fleisch deutlich mehr landwirtschaftliche Flächen als beispielsweise Gemüse und ist deutlich energieaufwendiger. Die Organisation NABU spricht davon, dass insgesamt 18% aller Treibhausgas-Emissionen auf die Fleischproduktion zurückzuführen ist.
ExpertInnen betonen deshalb immer wieder die wichtige Rolle des Fleischkonsums bei der Bekämpfung des Klimawandels. Ohne einen drastisch reduzierten Konsum werden die Klimaziele in Deutschland nicht zu erreichen sein. Um wie viel Kilogramm der Fleischkonsum fallen muss, kursieren in wissenschaftlichen Debatte unterschiedliche Zahlen, allerdings herrscht Einigkeit darüber, dass es sich um eine enorme Menge handelt. Die Deutsche Gesellschaft für Ernährung (DGE) empfiehlt beispielsweise einen pro Kopf-Fleischkonsum von weniger als 600 Gramm pro Woche, auf das Jahr gerechnet wären das ca. 31 Kilogramm. Zum Vergleich: Der Verbrauch im Jahr 2021 lag ungefähr beim 2,5-fachen dieses Wertes.
Einer Studie des WWF zufolge könnte sogar bereits die Halbierung des Fleischkonsums der Deutschen die ernährungsbedingten Treibhausgas-Emissionen um knapp 27% senken. Dies entspräche dem Erwärmungseffekt von 57 Tonnen Kohlendioxid.
Zumindest die Tendenz weist allerdings in die richtige Richtung. In den letzten Jahren verzichtet immer Menschen auf den täglichen Konsum von Fleisch. Auch der Markt veganer oder vegetarischer Ersatzprodukte boomt hierzulande, wodurch auch der Fleischkonsum pro Kopf in Deutschland abnimmt. Es stellt sich die Frage, ob sich dieser Trend in den nächsten Jahren verfestigen wird oder es sich nur um ein kurzzeitiges Phänomen handelt. Mit Hilfe der mathematischen Modellierung wollen wir eine Prognose für die nächsten Jahre liefern und dieser Frage auf den Grund gehen.
Ziel der Modellierung
[Bearbeiten]In unserem Modell möchten wir eine Prognose erstellen, wie sich der Fleischkonsum in Deutschland in den nächsten Jahren entwickeln könnte. Im Laufe der Modellierung versuchen wir unsere Vorhersagen stetig zu verbessern und den Fehler zwischen Prognose und tatsächlichen Daten stetig zu verringern. Das Modell soll außerdem als Grundlage dienen, die Prognose mit neueren Daten der nächsten Jahre ständig anzupassen und zu verbessern. Mit dem Wissen des Fleischkonsums pro Kopf in Deutschland kann dann beispielsweise entschieden werden, ob sich der Konsum wie gewollt verbessert oder mit anderen Maßnahmen möglicherweise nachgeholfen werden muss.
Schülerinnen und Schülern kann dieses Modell außerdem einen sinnvollen Einblick geben, wie sich der Fleischkonsum entwickelt und darauf aufbauend kann die Problematik, die ein hoher Fleischkonsum mit sich bringt, diskutiert werden.
Nutzergruppe
[Bearbeiten]- Sek I: Schüler*innen: Sensibilisieren für den Fleischkonsum, Aufmerksam auf Problematik machen, eigene erste Prognose erstellen und Trends beim Fleischkonsum erkennen
- Sek II: Industrie/ Verbraucher: Produktionsmenge (Fleisch, Fleischalternativen), Wie viel Fleisch wird in Zukunft noch gegessen?
- Uni: Politik: Genaue Prognose für nächsten Jahre kennen, Grundlage für Debatte über mögliche Maßnahmen, Auswirkungen von politischen Maßnahmen auf Fleischkonsum
Softwarenutzung
[Bearbeiten]- Tabellenkalkulationsprogramm (LibreOffice Calc)
- Dynamisches Geometriesystem (GeoGebra)
- Computeralgebraprogramm (Maxima)
Gruppenmitglieder
[Bearbeiten]- Nadine Borger
- Fabian Kempf
- Yannik Zimmermann
Wiki2Reveal
[Bearbeiten]- Einführung - (Foliensatz)

- Mathematische Grundlagen - (Foliensatz)

- Implementation - (Foliensatz)

- Modellierungszyklus 1 - (Foliensatz)

- Modellierungszyklus 2 - (Foliensatz)

- Modellierungszyklus 3 - (Foliensatz)

Modellierungszyklus 1 - Niveau Sekundarstufe I
[Bearbeiten]Datenerhebung
[Bearbeiten]Als Grundlage für den Modellierungszyklus wurden Daten zum deutschen Fleischkonsum des Bundesinformationszentrums Landwirtschaft (BZL) verwendet. Diese listet seit 1991 den jährlichen Pro-Kopf-Verbrauch in Deutschland auf. Zum Zeitpunkt der Modellierung standen uns Daten bis zum Jahr 2021 zur Verfügung. Ein Vorteil der Daten liegt daran, dass durch den erhobenen Pro-Kopf-Verbrauch die Daten vergleichbarer sind und Faktoren wie eine wachsende- bzw. schrumpfende Bevölkerung ignoriert werden können. In unserem Modell berücksichtigen wir außerdem keine statistischen Effekte, d.h. wir gehen von der selben Methodik zur Erhebung der Daten von 1991 bis 2021 aus.
Die Daten finden sich in der folgenden Tabelle:

| Jahr | Fleischkonsum pro Kopf in kg |
|---|---|
| 1991 | 95,3 |
| 1992 | 93,7 |
| 1993 | 95,5 |
| 1994 | 93,3 |
| 1995 | 92,4 |
| 1996 | 91,8 |
| 1997 | 90,6 |
| 1998 | 94,1 |
| 1999 | 94,9 |
| 2000 | 91,5 |
| 2001 | 88,8 |
| 2002 | 89,2 |
| 2003 | 90,5 |
| 2004 | 89,4 |
| 2005 | 88,4 |
| 2006 | 87,9 |
| 2007 | 91,1 |
| 2008 | 89,8 |
| 2009 | 90,1 |
| 2010 | 91,2 |
| 2011 | 91,4 |
| 2012 | 88,8 |
| 2013 | 89 |
| 2014 | 89,3 |
| 2015 | 89,9 |
| 2016 | 89,8 |
| 2017 | 88,1 |
| 2018 | 90,1 |
| 2019 | 85,5 |
| 2020 | 84,1 |
| 2021 | 81,7 |
Quelle: Bundesinformationszentrum Landwirtschaft (BZL)[1]
Erste Näherung: Lineare Regression
[Bearbeiten]Zunächst versuchen wir unsere Daten mit Hilfe der einfachen linearen Regression zu beschreiben. Als unabhängige Variable x werden dabei die jeweiligen Jahre definiert. Diese starten mit Beginn der Datenerhebung zum deutschen Fleischkonsum im Jahr 1991 und sollen im vorliegenden Diagramm bis ins Jahr 2050 reichen. Als abhängige Variable y betrachten wir den deutschen Pro-Kopf-Fleischverbrauch. Die Regressionsgerade wurde nun mit Hilfe der Tabellenkalkulation LibreOffice Calc erstellt. Sie wurde so gewählt, dass die quadratische Abweichung der einzelnen Datenpunkte zur Gerade minimal wird.
Lineare Funktion mit Hilfe der Regressionsgerade
[Bearbeiten]Wir erhalten dann die folgende Funktionsgleichung, wobei x für das Jahr und f(x) für den Pro-Kopf-Konsum steht.
Zu beachten ist, dass sich der y-Achsenabschnitt auf das Jahr 0 bezieht. Die Funktion macht also nur ab Beginn der Daten im Jahr 1991 Sinn. Die Steigung m beträgt -0,2633, das würde bedeuten, dass der Fleischkonsum Pro-Kopf jährlich um ca. -Kilogramm fällt.
Prognosewerte der linearen Funktion
[Bearbeiten]Mit Hilfe der obigen linearen Funktion können nur erste Prognosen für die folgenden Jahre erstellt werden. Im Folgenden sind einige Werte für den Fleischkonsum Pro-Kopf für ausgewählte Jahre aufgeführt:
Jahr 2023: ca. 85,7 kg/Kopf, Jahr 2025: ca. 85,2 kg/Kopf, Jahr 2030: ca. 83,9 kg/Kopf, Jahr 2040: ca. 81,3 kg/Kopf, Jahr 2050: ca. 78,7 kg/Kopf
Bewertung und Optimierung
[Bearbeiten]Legt man die vorhandenen Daten und die lineare Funktion zu Grunde, erkennt man den Trend eines abfallenden Fleischkonsums, der allerdings relativ gering ausfällt. Während die Datenpunkte zu Beginn noch um die Regressionsgerade streuen, wird der Fehler für die letzten erhobenen Daten besonders groß. Berechnet man mit der linearen Funktion den Konsum in den nächsten Jahren würde dieser im Vergleich zum letzten Wert 2021 erst einmal wieder zunehmen. Im Jahr 2040 würde der Konsum in etwa wieder den heutigen Wert annehmen. Dies erscheint doch sehr unrealistisch. Problematisch hierbei ist, dass dem stärker abnehmenden Trend von 2018-2021 keine Bedeutung zugemessen wird.
Ein weiteres Problem ist außerdem, dass die Gerade irgendwann die x-Achse schneiden würde, wodurch der Fleischkonsum in den negativen Bereich fallen würde. Es zeigen sich also bereits eklatante Schwächen bei der Modellierung mit einer linearen Funktion. Um Schülerinnen und Schüler einen ersten Trend erkennen zu lassen und eine Vorstellung für die Größenordnung zu entwickeln, erscheint das Modell dennoch sinnvoll.
Im nächsten Schritt suchen wir also einen anderen Funktionstypen, der uns realistischere Prognosen für den Fleischkonsum liefert. Dabei soll auch dem stärker abnehmenden Konsum in den letzten Jahre eine Bedeutung zugemessen werden.
Software
[Bearbeiten]- Tabellenkalkulation
Zweite Näherung: Funktionstypen im Vergleich
[Bearbeiten]Betrachtet man die einzelnen Datenpunkte, fällt auf, dass der Fleischkonsum in den 90er-Jahren eher stagniert. Er fällt zwar auch in einigen Jahren, dafür springt er dann zum Teil auch wieder nach oben, was besonders in den Jahren 1998 und 1999 zu beobachten ist. Auch in den 2000er-Jahren ist dieses Phänomen zu beobachten, wenn auch eine leichte Abwärtstendenz zu erkennen ist. Eine klare Abnahme des Konsums findet erst ab 2018 statt, seitdem fällt er aber auch in großen Schritten. Um die dargelegten Aspekte zu berücksichtigen, betrachten wir zunächst zwei Funktionstypen.
Exponentialfunktion
[Bearbeiten]Bei der Funktion (rote Funktion) handelt es sich um eine Exponentialfunktion. Wir betrachten den Graphen erst aber der Stelle x=0, da wir uns eine Prognose für die Zukunft anstreben und uns nicht für die Werte vor der Datenerhebung interessieren. Die Funktion konvergiert für x -> ∞ gegen 0 und verfügt über keine Nullstellen. Der Parameter a gibt den Anfangswert des Fleischkonsums an und der Parameter s staucht bzw. streckt den Graphen. Ihr Maximum befindet sich im Punkt (0|a). Im x-Bereich von 0 bis ∞ besitzt die Funktion außerdem eine Wendestelle.
Gebrochenrationale Funktion
[Bearbeiten]Die grüne Funktion ist eine gebrochenrationale Funktion. Die Funktion konvergiert ebenfalls für x -> ∞ gegen 0 und verfügt über keine Nullstellen. Sie ähnelt stark der Gaußfunktion, allerdings schmiegt sich die gebrochenrationale Funktion langsamer an die x-Achse an. Die Parameter sind identisch zu der Gaußfunktion. Das Maximum befindet sich ebenfalls im Punkt (0|a) und die Funktion verfügt auch über eine Wendestelle im positiven x-Bereich.

Geo-Gebra-Datei und Einstellen der Parameter
[Bearbeiten]Zunächst lassen wir uns beide Graphen in Geo-Gebra ploten. Zu beachten ist, dass das erste Jahr für das wir Daten besitzen (1991) als Jahr 0 festgelegt wird. Das x-Wert 30 repräsentiert also das aktuellste Jahr 2021. Nun tragen wir aber nicht alle Datenpunkte in Geo-Gebra ein, sondern konzentrieren uns auf zwei Datenpunkte. Dies hat den Vorteil, dass die beiden Punkte nun beide genau auf dem Graphen liegen. Wir wählen dafür den Beginn und das Ende unserer Datenreihe, also die Werte aus dem Jahr 1991 und 2021. Dafür lassen wir uns die Punkt D0 (0|95,3) und D30anzeigen. Sie liefert uns im Jahr 1991 (in unserem Fall Jahr 0) den Konsum von 95,3 kg/Kopf und im Jahr 2021 (in unserem Fall Jahr 30) den Konsum von 81,7 kg/Kopf (siehe Tabelle oben). Der Parameter a stellt das Maximum unserer Funktion und gleichzeitig den Funktionswert an der Stelle 0 dar. Diese setzen wir auf 95,3, da dies der Anfangswert unserer Datenreihe war. Der Parameter s soll nun so gewählt werden, dass der Graph durch den Wert des Fleischkonsums im Jahr 2021, also dem Punkt D30, geht. Da sich der Parameter s auf beide Funktion auswirkt, begnügen wir uns hier zuerst einmal mit einer näherungsweisen Einstellung. Somit laufen beide Graphen nun durch den Anfangspunkt D0 (0|95,3), der den Startwert unsere Datenreihe bzw. den Konsum im Jahr 1991 darstellt und ungefähr den Punkt D30 (30|81,7), den aktuellen Konsum im Jahr 2021.
Vergleich der beiden Graphen
[Bearbeiten]Sowohl die gebrochenrationale Funktion f(x), als auch die Exponentialfunktion g(x) stellen eine deutliche Verbesserung im Vergleich zu unserer ersten linearen Modellierung des Fleischkonsums dar. Im Bereich von 0 bis 30, in dem uns Daten vorliegen, sind sogar kaum Unterschiede der beiden Graphen zu erkennen. Erst danach verlaufen die Graphen erkennbar unterschiedlich, da sich die Funktion g(x) (rot markiert) deutlich schneller der x-Achse nähert. Da wir für die Prognose des Fleischkonsums das Fallen der Exponentialfunktion als zu steil erachten, entscheiden wir uns hier für die gebrochenrationale Funktion f(x).
Anpassung der Prognosefunktion
[Bearbeiten]Da wir uns nun für die gebrochenrationale Funktion mit der Funktionsgleichung entschieden haben, können wir nun die Parameter genau bestimmen. Ziel ist es, dass die Punkte D0 (0|95,3) und D30 (30|81,7) genau auf dem Graphen liegen. Der Parameter a ergibt sich gerade als Funktionswert an der Stelle x=0 und stellt gleichzeitig das Maximum unserer Funktion dar. Er beträgt für unsere Funktion also 95,3. Durch Einsetzen des Punktes D30 (30|81,7) und Parameter a=95,3 in die Funktionsgleichung ergibt sich nun . Mit Maxima lässt sich diese Gleichung beispielsweise mit der Funktion "solve" für s schnell lösen und es ergibt sich ein Wert von gerundet 73,5 für den Parameter.

Bewertung und Optimierung
[Bearbeiten]Im Vergleich zur ersten Näherung mit der linearen Regression konnte das Modell deutlich verbessert werden. Sowohl das Verhindern eines negativen Fleischkonsums als auch die Berücksichtigung einer stärkeren Abnahme in den letzten Jahren konnte umgesetzt werden. Die Funktion wurde nun so bestimmt, dass die Funktionswerte mit den vorliegenden Daten an zwei Punkten übereinstimmen, nämlich zu Beginn und zum Ende der Datenreihe. Allerdings wurden zur Vereinfachung nur zwei Punkte ausgewählt, weshalb die anderen Datenpunkte im Modell noch nicht berücksichtigt werden.
In Abbildung 4 kann die Prognosefunktion besser mit den vorliegenden Daten verglichen werden. Auf den ersten Blick scheint die gebrochenrationale Funktion eine gute Annäherung an den Fleischkonsum zu liefern. Ob sich die Funktion allerdings wirklich eignet, eine passende Prognose für den Fleischkonsum zu erstellen, soll nun im nächsten Schritt geprüft werden. Dazu soll der Fehler zwischen Prognosefunktion und den tatsächlichen Daten berechnet werden.

Software
[Bearbeiten]- LibreOffice Calc
- GeoGebra
- Maxima
Modellierungszyklus 2 - Sekundarstufe II
[Bearbeiten]Im Modellierungszyklus 1 haben wir unsere Prognose optimiert und schließlich die Funktion erhalten. Im weiteren Verlauf wollen wir nun berechnen, wie genau unsere Prognose ist. So kann nach Abschluss des jetzigen Modellierungszyklus entschieden werden, ob die Funktion tauglich ist und weiter optimiert werden kann oder eine andere Modellierung verwendet werden muss. Hierfür berechnen wir den absoluten und relativen Fehler unserer Funktion bezüglich der vorhandenen Daten.
Glättung durch gleitenden Mittelwert
[Bearbeiten]Um unsere Prognose besser mit den vorliegenden Daten zu vergleichen und dadurch auch weiter zu optimieren, berechnen wir den gleitenden Durchschnitt unserer Daten. Es entsteht eine Glättung der Datenreihe, wodurch einzelne Schwankungen ausgeglichen und dafür längerfristige Tendenzen deutlich gemacht werden. Mit Hilfe von LibreOffice haben wir den gleitenden Durchschnitt von jeweils vier Daten berechnet und als Diagramm darstellen lassen:

Berechnung des Flächeninhaltes unter der Prognosefunktion
[Bearbeiten]Um die Fehler zu berechnen, wollen wir die Flächeninhalte unter unserer Funktion f und unter dem gleitenden Durchschnitt ausrechnen und miteinander vergleichen. Um den Flächeninhalt unserer Funktion f zu bestimmen, berechnen wir das Integral mit den Grenzen 0 und 30.

Beim gleitenden Mittelwert berechnen wir den Flächeninhalt, in dem wir die Fläche in Trapeze unterteilen, von diesen jeweils den Flächeninhalt bestimmen und anschließend alle addieren.

Berechnung des Flächeninhalts unter der geglätteten Datenreihe
[Bearbeiten]Mit Hilfe von Trapezen haben wir den Flächeninhalt unter der geglätteten Datenreihe ausgerechnet. Hierbei gingen wir in kleineren Schritten auf der x-Achse voran und unterteilten den geglättet Graphen in mehrere Trapeze. Das erste Trapez begann bei dem Punkt (0|95,3) und Endete bei dem Punkt (5|93,25). Die x-Achse gibt den Fleischkonsum an und die y-Achse das jeweilige Jahr (Jahr 0 ist das Jahr 1991 und Jahr 30 das Jahr 2021). Dieses Prinzip setzten wir in 5 Jahresschritten fort, bis wir aufgrund von der Schneidung der Prognosefunktion variieren mussten, da der geglättete Mittelwert nun oberhalb der Prognosefunktion ist. Hierbei starteten wir wieder mit einem Schritt von 5 Jahren, anschließend von 4 Jahren und zu guter letzt von 3 Jahren. Somit hatten wir insgesamt sieben Trapeze. Anschließend bildeten wir die Summe der ersten vier Trapezen (unterhalb der Prognosefunktion) und die Summe der letzten drei Trapezen (oberhalb der Prognosefunktion):
Summe grüner Teil: 1656,9125
Summe roter Teil: 1068,8125
Als nächsten Schritt bestimmen wir das Integral unserer Prognosefunktion zum einen bis zum Schnittpunkt und zum anderen bis zum Jahr 30. Hierbei haben wir folgende Ergebnisse:
Integral 1: 1685,52
Integral 2: 1042,29
Relativer Fehler
[Bearbeiten]Um den relativen Fehler herausfinden zu können, subtrahieren wir vorerst unser Integral 1 mit der grünen Summe und Integral 2 mit der roten Summe. Dadurch erhalten wir den Unterschied zu den Integralen. Diese Ergebnisse lauten wie folgt:
grüne Summe - Integral 1 = 28,6075 (U.z.I. 1)
rote Summe - Integral 2 = 26,5225 (U.z.I. 2)
Absoluter Fehler insgesamt: 28,6075 + 26,5225 = 55,13
Mit diesen Ergebnissen können wir nun den relativen Fehler bestimmen. Dafür berechnen wir die gesamte Fläche unter unserer Datenreihe, also die grüne Summe plus die rote Summe:
1656,9125 + 1068,8125 = 2725,725
Anschließend teilen wir unseren absoluten Fehler durch die Gesamtfläche unter den Datenreihe:
= 0,02022581
Somit haben wir einen relativen Fehler von 2,02 % (gerundet).
Bewertung und Optimierung
[Bearbeiten]Für unsere Aussage ist der relative Fehler definitiv ausreichend, weshalb wir auch diese Funktion beibehalten werden. Jedoch wollen wir nun im nächsten Zyklus herausfinden, ob man die Parameter noch optimieren kann, sodass der Fehler geringer wird. Dies werden wir mit dem sogenannten Gradientenverfahren durchführen.
Modellierungszyklus 3 - Uni-Niveau
[Bearbeiten]Im folgendem Zyklus wollen wir mit Hilfe des Gradientenabstiegsverfahrens den Fehler der Prognose minimieren. Dafür versuchen wir die Parameter der Funktion so zu wählen, dass der Fehler zu den vorliegenden Daten minimal wird. Dazu benötigen wir zuerst die Fehlerfunktion und die dazugehörigen partiellen Ableitungen.
Fehlerfunktion und Partielle Ableitungen
[Bearbeiten]Die Fehlerfunktion soll ein Maß liefern für die Differenz zwischen unserer Prognose und den vorliegenden Daten. Wir betrachten dazu folgende Funktion: .
Mit der Funktion E(a,s) berechnen wir also das Mittel der quadratischen Abweichungen der Prognose und der Daten in Abhängigkeit der Parameter a und s. f(x_k,a,s) liefert uns dabei den Prognosewert in Abhängigkeit der Parameter und für ein bestimmtes k. Davon wird der Datenwert an der Stelle k abgezogen. Diese Abweichung wird quadriert, da mit dem quadratischen Fehler Ausgleichstendenzen vermieden werden. Die Summe läuft dabei von k=0 bis k=30, da für alle 31 Datenpunkte der quadratische Fehler berechnet und aufsummiert wird. Um diesen vergleichbar zu machen, wird die Summe durch die Anzahl der Datenpunkte geteilt.
Für das Gradientenabstiegsverfahren benötigen wir noch den Gradienten, der sich aus den partiellen Ableitungen nach a und s ergibt. Diese lassen sich einfach mit Maxima berechnen.
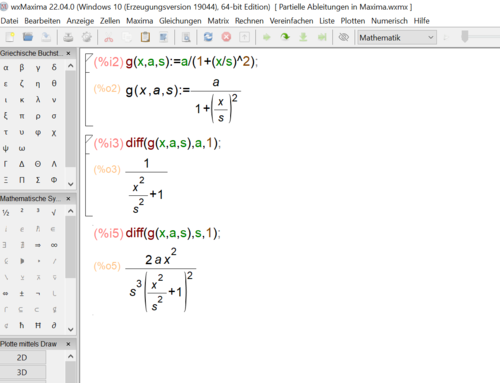
Daraus ergeben sich die beiden partiellen Ableitungen:
- partielle Ableitung nach a:
- partielle Ableitung nach s:
Ablauf Gradientenabstiegsverfahren
[Bearbeiten]Beim Gradientenabstiegsverfahren soll das Minimum der Fehlerfunktion E(a,s) gefunden werden. Im Folgenden sollen die Schritte zum Ablauf des Verfahrens stichpunktartig erläutert werden:
1.Schritt: Wählen eines Startpunktes und lege eine Schrittweite fest
2.Schritt: Berechne den Fehler mit den Startwerten mit Hilfe der Fehlerfunktion E(a,s)
3.Schritt: Berechne den Gradienten an der Stelle mit Hilfe der partiellen Ableitungen
4.Schritt: Berechne die Länge des Gradienten
5.Schritt: Verschiebe in entgegengesetzte Richtung des Gradienten und normiere diesen auf die festgelegte Schrittweite
6.Schritt: Überprüfe mit der Fehlerfunktion E(a,s), ob sich der Fehler verringert hat
7.Schritt: Falls sich der Fehler nicht verringert hat: Halbiere die Schrittweite und gehe zurück zu Schritt 5
8.Schritt: Wiederhole die Schritte 3 bis 7 solange, bis sich der Fehler kaum noch verändert
Durchführung des Gradientenabstiegsverfahren
[Bearbeiten]Die eben beschriebenen Schritte haben wir mit einer Tabellenkalkulation umgesetzt. Hier kann das Verfahren beliebig lang ausgeführt werden. Wir beginnen mit den Startwerten , da dies die Parameter sind, die wir zum Ende des 1.Modellierungszyklus bestimmt haben.
Im Folgenden sieht man einen Auszug des Gradientenabstiegsverfahren in LibreOffice Calc.

Nach vielen Iterationsschritten konvergiert das Verfahren gegen folgende Werte:

Ergebnisse
[Bearbeiten]Das Gradientenabstiegsverfahren minimiert den Fehler E(a,s) deutlich. Es konvergiert gegen die Werte a ≈ 92,81 und s ≈ 101,91. Man sieht also, dass sich die Parameter im Vergleich zu den Ausgangswerten aus Zyklus 1 stark verändert haben. Dort hatten wir die Parameter so bestimmt, dass die Prognosefunktion f(x) genau durch den ersten und letzten Datenpunkt verläuft, die anderen Datenpunkte aber vernachlässigt. Der Fehler konnte mit dem Verfahren von einem Ausgangswert von ca. 7,57 auf 3,65 mehr als halbiert werden.
Die verbesserte Prognosefunktion sieht nun wie folgt aus:

Die optimierte Prognosefunktion f(x) ist in diesem Diagramm grün dagestellt. Man erkennt die Veränderung im Vergleich zum Graphen aus den ersten beiden Zyklen (grau unterlegt).
Bewertung und Optimierung
[Bearbeiten]Im 3.Modellierungszyklus konnten wir die ohnehin schon gute Prognosefunktion deutlich optimieren. Der Fehler hat sich dabei noch einmal mehr als halbiert. Betrachtet man nun auszugsweise einige Werte für die folgenden Jahre, kommt man auf folgenden Ergebnisse:
2025: ca. 83,51 kg/Kopf; 2030: ca. 80,95 kg/Kopf; 2035: ca. 78,23 kg/Kopf; 2040: ca. 75,38 kg/Kopf; 2045: ca. 72,46 kg/Kopf; 2050: ca. 69,51 kg/Kopf; 2060: ca. 63,64 kg/Kopf
Die Werte erscheinen auf den ersten Blick durchaus realistisch. Ein weiterhin bestehendes Problem ist allerdings, dass sich der Fleischkonsum laut Prognose in den nächsten Jahren wieder leicht erhöhen würde (siehe Prognose 2025: 83,51 kg/Kopf und gemessener Wert 2021: 81,7 kg/Kopf). Trotzdem liefert die Prognose nutzbare Ergebnisse, besonders wenn die etwas weiter in der Zukunft liegenden Werte betrachtet werden.
Mit den vorliegenden Daten kann diese Prognosefunktion aktuell nicht verbessert, da wir das Minimum der Fehlerfunktion bereits gefunden haben. Für eine noch genauere Prognose würde ein anderer Funktionstyp benötigt werden.
Allerdings kann sich die Prognose durch weitere Daten in den nächsten Jahren durchaus verbessern. Werden diese neuen Daten im Gradientenabstiegsverfahren verwendet, kann der Algorithmus gegen andere Werte für die Parameter a und s konvergieren.
Mathematische Theorie für Modellierungszyklus 1: Sekundarstufe I
[Bearbeiten]Einfache lineare Regression
[Bearbeiten]Bei der einfachen linearen Regression betrachten wir den linearen Zusammenhang zwischen einer abhängigen Variablen (Kriterium) und einer unabhängigen Variable (Prädiktor).
Ziel ist es, mit Hilfe der Prädiktorvariable eine Vorhersage für die Werte der Kriteriumsvariable zu finden.
Regressionsgleichung
[Bearbeiten]: Vorhergesagter Wert auf dem Kriterium y für den jeweiligen Messwert
: Messwert auf dem Prädiktor x (Wert der Variablen, die zur Vorhersage genutzt wird)
: Regressionsgewicht/ -koeffizent, Steigung der Regressionsgeraden
:y-Achsenabschnitt der Regressionsgeraden
Berechnung der Regressionsgleichung:
- Vorrausetzung: Daten mit zwei verschiedenen Variablen (Kriterium und Prädiktor)
- Berechnung arithmetisches Mittel:
- Bilden der Summe der quadratischen Abweichungen :
- Bilden der Summe der Abweichungsprodukte von x und y:
- Gesucht ist nun die minimale quatratische Abweichung. Betrachtet man die Summenfunktion als Funktion der beiden Variablen x und y, lässt sich mithilfe der partieller Ableitung ein lineares Gleichungssystem zur Bestimmung der Nullstelle bilden. Durch Umformen der Gleichungen, lässt sich die Steigung der gesuchten Gerade berechnen :
- Mit Hilfe des Verschiebungssatzes kann man die Formel auch vereinfacht darstellen :
- Als letztes lässt sich mit der y-Achsenabschnitt der gesuchten Geraden berechnen
Regressionsgerade einzeichnen
- lineare Gleichungen der Form : in ein Koordinatensystem einzeichnen
Gebrochenrationale Funktion
[Bearbeiten]Grundlagen
[Bearbeiten]- Allgemeine Form:
mit natürlichen Zahlen und
- Einfluss verschiedener Parameter bei der gewählten Funktion:

- a: Verschiebung des Maximums/Minimums auf der y-Achse
- s: Graf wird steiler/flacher
natürliche Exponentialfunktion
[Bearbeiten]- auch "e-Funktion" genannt
- Definition: Funktionen, der Form →, x→ , wobei e die eulersche Zahl ist.
Grenzverhalten e-Funktion
[Bearbeiten]- x-Achse ist waagrechte Asymptote
- durch Parameter oder Verkettungen der e-Funktion mit anderen Funktionen ändert sich die Asymptote
Verkettete e-Funktion und Einfluss von Parametern
[Bearbeiten]GeoGebra verdeutlich anschaulich die Einflussfaktoren der gewählten Parameter:

- Parameter a: Verschiebung des Schnittpunktes mit y-Achse mit Streckung und Stauchung
- Parameter s: Streckung und Stauchung, wobei Schnittpunkt mit y-Achse unverändert bleibt
- Implementation des Modells mit: Tabellenkalkulation, Maxima, Geogebra, Octave, R-Studio, ...
Mathematische Theorie für Modellierungszyklus 2: Sekundarstufe Ⅱ
[Bearbeiten]Gleitender Mittelwert
[Bearbeiten]- Methode zur Glättung von Datenreihen
- Folge von arithmetische Mittelwerten über eine sich ändernde aber gleich groß bleibende Untermenge der insgesamt erhobenen Werte
- einfacher gleitender Durchschnitt n-ter Ordnung:
Flächeninhalt unter einer Kurve mit Hilfe von Trapezen bestimmen
[Bearbeiten]- Die Fläche zwischen der Kurve und der x-Achse wird in mehrere Trapeze unterteilt, deren Flächeninhalte ausgerechnet und anschließend addiert werden.
- Formel für den Flächeninhalt eines Trapez:
Integralrechnung
[Bearbeiten]- Stammfunktion bilden (gegebenenfalls mit Computeralgebrasystem)
- Grenzen wählen und in Stammfunktion einsetzen
Mathematische Theorie für Modellierungszyklus 3: Uni-Niveau
[Bearbeiten]Differenzieren
[Bearbeiten]- Partielle Ableitung: Ableiten einer Funktion mit mehreren Variablen nach einer Variablen
- Gradient: Vektor aus den ersten partiellen Ableitungen
Gradienteabstiegsverfahren
[Bearbeiten]siehe Gradientenabstiegsverfahren
Idee
[Bearbeiten]- Verfahren, um allgemeine Orientierungsprobleme zu löse
- Minimierungsverfahren: man startet bei Näherungswert und geht schrittweise in Richtung des negativen Gradienten bis man keine Verbesserung mehr der Näherungswerte erhält
Animation
[Bearbeiten]Verfahren
[Bearbeiten]- Fehlerfunktion bilden
- Gradient aus partiellen Ableitungen bilden (Gradient gibt Steigung an)
- Gradient normieren: Länge/Norm berechnen: , mit Kehrwert multiplizieren
- negativer Gradient zeigt in die Richtung, in der die Funktionswerte fallen
- falls man bei einem Iterationsschritt über Maximum springt, wird die Schrittweite verkleinert
- Abbruchkriterium: wenn der Gradient null ist
Softwarenutzung
[Bearbeiten]LibreOffice Calc
[Bearbeiten]Im Modellierungszyklus 1 verwenden wir Calc, um unsere Daten zuerst in tabellarischer Form und anschließend als Diagramm darzustellen. Dazu geben wir zuerst unsere Daten in zwei unterschiedliche Spalten ein (A: Jahr, B:Fleischkonsum). Anschließend markieren wir alle Daten und wählen in der Befehlleiste unter "Einfügen" ein Punktdiagramm aus. Nun werden automatisch ein Diagramm erstellt mit Spalte 1 auf der x-Achse und Spalte 2 auf der y-Achse.
Anschließend verwende wir die Funktion "Trendlinie", um eine lineare Regressionsgerade im Diagramm zu erzeugen. Hierbei können wir unter "weiteren Optionen" auch die Gleichung der Regressionsgerade anzeigen lassen.
Außerdem verwenden wir Calc, um den gleitenden Durchschnitt unserer Datenreihe zu berechnen. Hierfür erstellen wir eine Tabelle mit fünf Spalten:
- Spalte A: "Delta x" von 0 bis 30, gibt den Abstand vom jeweiligem Jahr zum Startzeitpunkt an
- Spalte B: Prognose, bestimmt den Funktionswert unserer Funktion von x bzw. "Delta x" (z.B. wenn in Zelle A2 Delta x gleich 1 ist, schreiben wir in die Zelle rechts daneben "=95,3/1+(A2/73,5)^2" und erhalten somit den Funktionswert von f(1))
- Spalte C: vergangene Jahre seit Startzeitpunkt (identisch zu Spalte A)
- Spalte D: vorliegende Daten zum Konsum aus unserer Anfangstabelle
- Spalte E: gleitender Mittelwert, bestimmt den Mittelwert von jeweils vier Daten (z.B. "=MITTELWERT(D4:D7) bestimmt den Mittelwert der Daten in D4, D5, D6, und D7)
Anschließend erstellen wir ein Diagramm mit Spalte A auf der x-Achse und Spalte B auf der y-Achse. Dadurch erhalten wir den Graf zu unserer Funktion f(x). Um diesen mit dem gleitenden Mittelwert zu vergleichen, fügen wir Spalte E mit den berechneten Mittelwerten ebenfalls in unser Diagramm ein (Rechtsklick auf Diagramm, "Daten auswählen", "Hinzufügen", Spalte E markieren und auf "Ok" klicken).

Im Modellierungszyklus 2 verwenden wir Calc, um den Flächeninhalt der geglätteten Daten mit Hilfe der Trapezmethode zu berechnen. Hierfür erstellen wir ein Tabellenblatt mit 4 Spalten.
- Spalte A: Länge Seite a (y-Wert des ersten Punktes)
- Spalte B: Länge Seite c (y-Wert des nächsten Punktes)
- Spalte C: Höhe h (Abstand der beiden Punkte)
- Spalte D: Flächeninhalt "=1/2*(A2+B2)*C2" (1/2*(a+b)*h)

Im Modellierungszyklus 3 haben wir das Gradientenabstiegsverfahren mit Hilfe von Calc angewendet:
- Gelb unterlegten Felder können beliebig verändert werden (Startpunkt und Schrittweite)
- Ob Verbesserung vorliegt, kann schnell durch grüne oder rote Farbe festgestellt werden
- 1. und 2.Spalte: Bestimmung der Parameter a und s
- Neue Werte werden übernommen, wenn sich Fehler verbessert - Beibehaltung, wenn sich Fehler verschlechtert
- 3. und 4.Spalte: Berechnung des Gradienten mit Hilfe der partiellen Ableitungen
- 5.Spalte: Schrittweite
- wird beibehalten, wenn sich der Fehler minimiert
- wird halbiert, wenn sich der Fehler nicht verbessert
- 6.Spalte und 7.Spalte: Normierung des entgegengesetzten Gradienten auf Schrittweite
- 8.Spalte: Berechnung der Länge des Gradienten
- 9.Spalte: Berechnung des Fehlers aus vorherigen Iterationsschritt
- 10.Spalte: Berechnung des Fehlers mit veränderten Werten
- 11.Spalte: Prüfung, ob Optimierung vorliegt

GeoGebra
[Bearbeiten]Im Modellierungszyklus 1 verwenden wir GeoGebra um uns unseren Daten des Fleischkonsum durch verschiedene Funktionen anzunähern. Wir haben uns hierbei für eine gebrochen-rationale Funktion und eine e-Funktion mit verschiedenen Parametern entschieden. Um die Funktion bei GeoGebra zu plotten, muss man diese einfach im Eingabefeld mit entsprechenden Variablen für die jeweiligen Parametern eingeben. Dabei erzeugt GeoGebra automatisch für jeden Parameter einen Schieberegler. Die Schieberegler kann man beispielsweise noch bzgl. möglicher Werte (min. und max.), Position und Schrittweite ("Speed") bearbeiten.

Maxima
[Bearbeiten]Im Modellierungszyklus 2 verwenden wir Maxima um unsre gebrochenrationale Funktion zu integrieren. Dafür definieren wir zuerst die Funktion mit "f(x):= 95,3/(1+(x/77,5)^2)". Danach können wir mit der Funktion "Integrate(f(x),x,0,18" den Flächeninhalt unter der Funktion in den Grenzen 0 bis 18 berechnen und mit "Integrate(f(x),x,18,30)" den restlichen Teil.
Im Modellierungszyklus 3 benötigen wir partielle Ableitungen. Diese können wir ebenfalls mit Maxima berechnen. Zuerst definieren wir wieder unsere Funktion mit "g(x,a,b):=a/(1+(x/b)^2)". Dann können wir mit der Funktion "diff(g(x,a,b),a,1)" beispielsweise die erste partielle Ableitung nach a berechnen (dg/da).
Quellennachweis
[Bearbeiten]- ↑ Quelle: Bundesinformationszentrum Landwirtschaft (BZL)








































