Kurs:Topologische Invertierbarkeitskriterien/T-Stetigkeit Cauchy-Produkt
Einleitung
[Bearbeiten]Diese Seite kann als Wiki2Reveal Folien angezeigt werden. Einzelne Abschnitte werden als Folien betrachtet und Änderungen an den Folien wirken sich sofort auf den Inhalt der Folien aus.
Zielsetzung
[Bearbeiten]Diese Lerneinheit in der Wikiversity hat das Ziel, die Polynomalgebra in einer Weise zu topologisieren, damit einerseits die Cauchy-Multiplikation auf stetig ist und andererseits über die Abschätzungen der Quotientengaugefunktionale auf ein Algebraisomorphismus existiert, bei dem sowohl als auch stetig ist.
Veranschaulichung Beweisidee
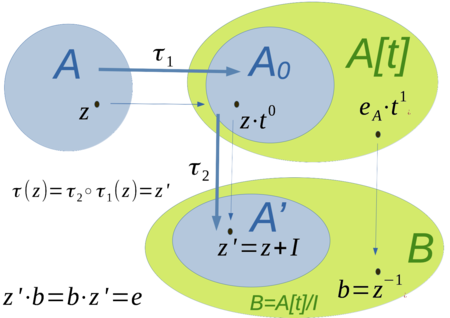
[Bearbeiten]Bei der Konstruktion der Algebraerweiterung, in der ein invertierbar ist, wird in einem ersten Schritt die Algebra der Polynome betrachtet. Die folgende Abbildung zeigt, wie die Algebraerweiterung über die Polynomalgebra konstruiert wird.
Zielgruppe
[Bearbeiten]Die Zielgruppe der Lerneinheit sind Studierende der Mathematik im Master.
Aufgaben für Lernende / Studierende
[Bearbeiten]Siehe auch
[Bearbeiten]- LC-Stetigkeit Cauchy-Produkt
- PC-Stetigkeit Cauchy-Produkt
- LC-Regularität
- PC-Regularität
- T-Regularität
Seiteninformation
[Bearbeiten]Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.
Wiki2Reveal
[Bearbeiten]Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Topologische Invertierbarkeitskriterien' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.
- Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
- Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Topologische%20Invertierbarkeitskriterien/T-Stetigkeit%20Cauchy-Produkt
- siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.

![{\displaystyle A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13daf73f25e64310e7e5d67c5aa8dd4f97cb884f)
![{\displaystyle B:=A[t]/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bc806fa49af6a80a0b8ba7a4eb54a8d503dd8ab)