Wenn wir die  -Regularität eines Elementes
-Regularität eines Elementes  für eine lokalkonvexe topologische Algebra
für eine lokalkonvexe topologische Algebra  sprechen, suchen wir nach einer lokalkonvexen Algebraerweiterungen
sprechen, suchen wir nach einer lokalkonvexen Algebraerweiterungen  von
von  in der
in der  invertierbar ist. Dabei besteht
invertierbar ist. Dabei besteht
 und
und
aus einem System von Halbnormen, die die Topologie auf  bzw.
bzw.  erzeugen.
erzeugen.
Zielsetzung einer lokalkonvexe Algebraerweiterung  zu einer gegebenen topologischen Algebra
zu einer gegebenen topologischen Algebra  mit
mit  ist es, die gegebene lokalkonvexe Algebraerweiterung so zu vergrößern, dass diese ein inverses Element
ist es, die gegebene lokalkonvexe Algebraerweiterung so zu vergrößern, dass diese ein inverses Element  in der lokalkonvexen Algebraerweiterung
in der lokalkonvexen Algebraerweiterung  besitzt. Als topologieerzeugende
besitzt. Als topologieerzeugende  -Gaugefunktionale werden hier Halbnormen
-Gaugefunktionale werden hier Halbnormen  und
und  verwendet.
verwendet.
LC-Singularität und topologisch kleine Potenzen
[Bearbeiten]Für kommutative lokalkonvexe Algebren  mit unital positivem Halbnormensystem
mit unital positivem Halbnormensystem  erhält man folgende Charakterisierung:
erhält man folgende Charakterisierung:
 (topologisch kleine Potenzen)
(topologisch kleine Potenzen) 

 -singulär
-singulär
Für kommutative lokalkonvexe Algebren  mit unital positivem
mit unital positivem  -Halbnormensystem
-Halbnormensystem  erhält man folgende Charakterisierung:
erhält man folgende Charakterisierung:
 erfüllt das LC-Regularitätskriterium
erfüllt das LC-Regularitätskriterium 

 -regulär
-regulär
Ein Element  besitzt genau
besitzt genau  -regulär in
-regulär in  , wenn es für alle
, wenn es für alle  ein
ein  und eine isotone Folge von Halbnormen
und eine isotone Folge von Halbnormen  mit positiven Konstanten
mit positiven Konstanten  gibt, für die gilt:
gibt, für die gilt:
- (LC1)
 für alle
für alle  und
und  und
und
- (LC2)
 für alle
für alle  und
und  .
.
Algebraerweiterung  von
von  ist hier eine lokalkonvexe Algebra, die ein inverses Element
ist hier eine lokalkonvexe Algebra, die ein inverses Element  zu einem gegebenen
zu einem gegebenen  enthält.
enthält.
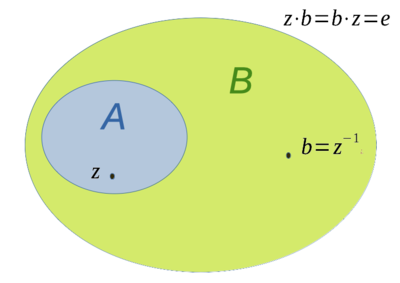
Sei  die Klasse der lokalkonvex unitalen Algebren und
die Klasse der lokalkonvex unitalen Algebren und  . Die Algebraerweiterung
. Die Algebraerweiterung  bzw.
bzw.  -Erweiterung von
-Erweiterung von  benötigt nach Definition es einen Algebraisomorphismus
benötigt nach Definition es einen Algebraisomorphismus
 mit:
mit:
 , wobei
, wobei  ist das Einselement von
ist das Einselement von  und
und  das Einselement von
das Einselement von  ist.
ist. ist homöomorph zu
ist homöomorph zu  ; d.h.
; d.h.  und
und  sind stetig.
sind stetig.
Veranschaulichung - Algebraisomorphismus
[Bearbeiten]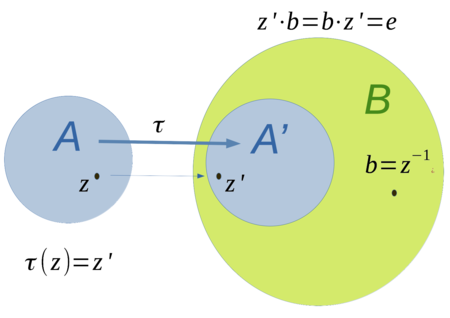
Algebraisomorphismus - Einbettung in die Algebraerweiterung
[Bearbeiten]- Im allgemeinen identifiziert man
 mit
mit  und schreibt
und schreibt  . In der jeweiligen Konstruktion der Algebraerweiterung sieht man, dass die Element aus
. In der jeweiligen Konstruktion der Algebraerweiterung sieht man, dass die Element aus  mit Elementen
mit Elementen  in einem Quotientenraum
in einem Quotientenraum ![{\displaystyle B:=A[t]/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bc806fa49af6a80a0b8ba7a4eb54a8d503dd8ab) identifiziert werden.
identifiziert werden.
- Sei
 eine Nullumgebungsbasis der Relativtopologie von
eine Nullumgebungsbasis der Relativtopologie von  auf
auf  und
und  eine Nullumgebungsbasis von
eine Nullumgebungsbasis von  , dann kann man die Homöomorphie zwischen
, dann kann man die Homöomorphie zwischen  und
und  wie immer über die Topologie ausdrücken:
wie immer über die Topologie ausdrücken:

Betrachtet man die Halbnormen  und
und  für Nullumgebungen, so lassen sich die oberen beiden Aussagen wie folgt umformulieren (siehe auch Stetigkeitssatz für lineare Abbildungen):
für Nullumgebungen, so lassen sich die oberen beiden Aussagen wie folgt umformulieren (siehe auch Stetigkeitssatz für lineare Abbildungen):

Wesentliche Schritte bei der Konstruktion der Algebraerweiterung
[Bearbeiten]Wir betrachten zunächst multiplikative kommuntative Algebren  .
.
- Ausgehend von
 wird die Polynomalgebra
wird die Polynomalgebra ![{\displaystyle (A[t],\|\!|\cdot |\!\|_{A[t]})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82e2ba8615c5a5ac87919d1789448041953c3382) mit einer Halbnorm
mit einer Halbnorm ![{\displaystyle \|\!|\cdot |\!\|_{A[t]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8f07324e76fbb15bdd056870b423030bfddc0f9) topologisiert.
topologisiert.
- Halbnorm
![{\displaystyle \|\!|\cdot |\!\|_{A[t]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8f07324e76fbb15bdd056870b423030bfddc0f9) macht
macht ![{\displaystyle A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13daf73f25e64310e7e5d67c5aa8dd4f97cb884f) zu einer topologischen Algebra, wobei die Stetigkeit der algebraischen Operationen (insbesondere die Stetigkeit der Cauchy-Multiplikation) nachzuweisen ist.
zu einer topologischen Algebra, wobei die Stetigkeit der algebraischen Operationen (insbesondere die Stetigkeit der Cauchy-Multiplikation) nachzuweisen ist.
- Übergang zu dem Quotientenraum
![{\displaystyle B:=A[t]/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bc806fa49af6a80a0b8ba7a4eb54a8d503dd8ab) , wobei das Polynom
, wobei das Polynom  das Hauptideal
das Hauptideal ![{\displaystyle I:=o\cdot A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a1c9cd3681d946591cd8913c805b574013e3ed1) definiert und
definiert und ![{\displaystyle o\in A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/084c9c353b0712820bde88d340156c6b728117d2) ein Repräsentant des Nullvektors
ein Repräsentant des Nullvektors  in
in  ist.
ist.
- Die Konstruktion des Ideals
 liefert die algebraische Invertierbarkeit, denn mit
liefert die algebraische Invertierbarkeit, denn mit  ist
ist ![{\displaystyle b_{I}:=b+I\in B=A[t]/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c03c485d01d92401bcc1ac0b66022507b46a83c) das inverse Element zu
das inverse Element zu  mit
mit  mit
mit  bzw.
bzw.  . Die Kommutativität liefert dann, dass auch
. Die Kommutativität liefert dann, dass auch  gilt.
gilt.
Zelazko hat die  -regulären Elemente[1] 1984 über die folgende Bedingung charakterisiert. Dabei liefert die von Zelazko angegebene Bedingung unmittelbare eine Topologisierung der Polynomalgebra, wobei die Topologie auf dem Quotientenraum
-regulären Elemente[1] 1984 über die folgende Bedingung charakterisiert. Dabei liefert die von Zelazko angegebene Bedingung unmittelbare eine Topologisierung der Polynomalgebra, wobei die Topologie auf dem Quotientenraum ![{\displaystyle B:=A[t]/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bc806fa49af6a80a0b8ba7a4eb54a8d503dd8ab) , in der ein gegebenes
, in der ein gegebenes  invertierbar ist, immer noch die Punkte von
invertierbar ist, immer noch die Punkte von  über den Algebraisomorphismus
über den Algebraisomorphismus  trennt.
trennt.
Satz: LC-Charakterisierung nach Zelazko
[Bearbeiten]Sei  , dann gilt: Ein Element
, dann gilt: Ein Element  ist genau dann
ist genau dann  -regulär, falls es für alle
-regulär, falls es für alle  ein
ein  und eine Folge positiver Zahlen
und eine Folge positiver Zahlen  gibt, so dass
gibt, so dass

für alle endlichen Folgen  in
in  gilt.
gilt.
Für den Beweis der  -Charakterisierung muss man die Koeffizienten
-Charakterisierung muss man die Koeffizienten  so vergrößeren, dass die Cauchy-Multiplikation auf
so vergrößeren, dass die Cauchy-Multiplikation auf ![{\displaystyle A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13daf73f25e64310e7e5d67c5aa8dd4f97cb884f) stetig ist.
stetig ist.
- Seien
 die Halbnormen auf
die Halbnormen auf ![{\displaystyle B:=A[t]/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bc806fa49af6a80a0b8ba7a4eb54a8d503dd8ab) . Zeigen Sie, dass die Halbnorm folgende Eigenschaft erfüllt:
. Zeigen Sie, dass die Halbnorm folgende Eigenschaft erfüllt:  für alle
für alle  .
.
- Erläutern Sie über die Definition des Ideals, warum das Kriterium von Zelazko die obigen Summen erzeugen.
LC-Charakterisierung über topologische große Potenzen
[Bearbeiten]Die Charakterisierung der  -regulären Elemente kann man als Spezialfall der pseudokonvexen kommutativen Algebren auffassen (siehe
-regulären Elemente kann man als Spezialfall der pseudokonvexen kommutativen Algebren auffassen (siehe  -Regularität), wobei für alle
-Regularität), wobei für alle  -Halbnormen
-Halbnormen  gesetzt wird. Die Topologisierung der Polynomalgebra erfolgt dann analog über eine Halbnorm statt Quasihalbnorm
gesetzt wird. Die Topologisierung der Polynomalgebra erfolgt dann analog über eine Halbnorm statt Quasihalbnorm  und damit werden die Koeffizienten
und damit werden die Koeffizienten  von
von  gemessen und gehen mit
gemessen und gehen mit  additiv in den Wert des Halbnorm
additiv in den Wert des Halbnorm  ein. Für das genau Vorgehen siehe (siehe
ein. Für das genau Vorgehen siehe (siehe  -Regularität).
-Regularität).
- ↑ Zelazko Wieslaw, (1984), Concerning characterization of permanently singular elements in commutative locally convex algebras, Mathematical Structures – Computational Mathematics – Mathematical Modelling 2, Sofia, S. 326-333
Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.
Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Topologische Invertierbarkeitskriterien' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.














































![{\displaystyle B:=A[t]/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bc806fa49af6a80a0b8ba7a4eb54a8d503dd8ab)







![{\displaystyle (A[t],\|\!|\cdot |\!\|_{A[t]})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82e2ba8615c5a5ac87919d1789448041953c3382)
![{\displaystyle \|\!|\cdot |\!\|_{A[t]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8f07324e76fbb15bdd056870b423030bfddc0f9)
![{\displaystyle A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13daf73f25e64310e7e5d67c5aa8dd4f97cb884f)

![{\displaystyle I:=o\cdot A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a1c9cd3681d946591cd8913c805b574013e3ed1)
![{\displaystyle o\in A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/084c9c353b0712820bde88d340156c6b728117d2)



![{\displaystyle b_{I}:=b+I\in B=A[t]/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c03c485d01d92401bcc1ac0b66022507b46a83c)




















