Kurs:Topologische Invertierbarkeitskriterien/PC-Regularität

Einführung

Wenn wir die ${\mathcal {PC}}$ -Regularität eines Elementes $z\in A$ für eine pseudokonvexe topologische Algebra $(A,\|\cdot \|_{\mathcal {A}})$ sprechen, suchen wir nach einer pseudokonvexen Algebraerweiterungen $(B,\|\cdot \|_{\mathcal {B}})$ von $(A,\|\cdot \|_{\mathcal {A}})$ in der $z\in A$ invertierbar ist. Dabei besteht

$\|\cdot \|_{\mathcal {A}}:=\{\|\cdot \|_{\alpha }\,:\,\alpha \in {\mathcal {A}}\}$ und
$\|\cdot \|_{\widetilde {\mathcal {A}}}:=\{\|\cdot \|_{\widetilde {\alpha }}\,:\,{\widetilde {\alpha }}\in {\widetilde {\mathcal {A}}}\}$

Systeme von $p$ -Halbnormen mit $p\in (0,1]$ sind, die die Topologie auf $A$ bzw. $B$ erzeugen.

Zielsetzung

Zielsetzung einer pseudokonvexe Algebraerweiterung $(B,\|\cdot \|_{\mathcal {B}})$ zu einer gegebenen topologischen Algebra $(A,\|\cdot \|_{\mathcal {A}})$ mit $z\in A$ ist es, die gegebene pseudokonvexe Algebraerweiterung so zu vergrößern, dass diese ein inverses Element $z^{-1}:=b\in B$ in der pseudokonvexen Algebraerweiterung $B$ besitzt. Als topologieerzeugende $p$ -Gaugefunktionale werden hier $p$ -Halbnormen $\|\cdot \|_{\mathcal {A}}$ und $\|\cdot \|_{\widetilde {\mathcal {A}}}$ verwendet. Dieses Ziel ist eine kleine Erweiterung einer äquivalenten Charakterisierung von Zelazko (1984)^[1] für lokalkonvexe Räume^[2].

Topologisch kleine Potenzen und PC-Singularität

Für kommutative pseudokonvexe Algebren $(A,\|\cdot \|_{\mathcal {A}})$ mit unital positivem $p$ -Halbnormensystem $\|\cdot \|_{\mathcal {A}}$ erhält man folgende Charakterisierung:

z\in {\mathcal {TKP}}(A)

(topologisch kleine Potenzen)

\Longrightarrow

z\in A

{\mathcal {PC_{e}^{k}}}

-singulär

Charakterisierung der PC-Regularität

Für kommutative pseudokonvexe Algebren $(A,\|\cdot \|_{\mathcal {A}})$ mit unital positivem $p$ -Halbnormensystem $\|\cdot \|_{\mathcal {A}}$ erhält man folgende Charakterisierung:

z\in A

erfüllt das PC-Regularitätskriterium

\Longleftrightarrow

z\in A

{\mathcal {PC_{e}^{k}}}

-regulär

PC-Regularitätskriterium

Ein Element $z\in A$ besitzt genau ${\mathcal {PC}}_{e}^{k}$ -regulär in ${\textstyle \left(A,\left\|\cdot \right\|_{\mathcal {A}}\right)\in {\mathcal {PC}}_{e}^{k}}$ , wenn es für alle ${\textstyle \alpha \in {\mathcal {A}}}$ ein ${\textstyle \beta \in {\mathcal {A}}}$ und eine isotone Folge von Quasihalbnormen ${\textstyle \left(\left\|\cdot \right\|_{(\alpha ,k)}\right)_{k\in \mathbb {N} _{0}}}$ mit der Stetigkeitskonstante der Addition $K_{\alpha }\geq 1$ und positive Konstanten ${\textstyle D_{(\alpha ,k)}}$ gibt, für die gilt:

(PC1) ${\textstyle \left\|x\right\|_{\alpha }\leq \left\|x\right\|_{(\alpha ,k)}\leq D_{(\alpha ,k)}\cdot \left\|x\right\|_{\beta }}$ für alle ${\textstyle x\in A}$ und ${\textstyle k\in \mathbb {N} _{0}}$ und
(PC2) ${\textstyle \left\|x\right\|_{(\alpha ,k)}\leq \left\|z\cdot x\right\|_{(\alpha ,k+1)}}$ für alle ${\textstyle x\in A}$ und ${\textstyle k\in \mathbb {N} _{0}}$ .

Bemerkung

Die Stetigkeitskonstante der Addition $K_{\alpha }\geq 1$ kann dabei für alle Quasihalbnormen ${\textstyle \left\|\cdot \right\|_{(\alpha ,k)}}$ mit ${\textstyle k\in \mathbb {N} _{0}}$ gewählt werden.

Stetigkeitskonstante der Addition

Die Stetigkeitskonstante der Addition $K_{\alpha }$ gilt für alle Quasihalbnormen $\left\|\cdot \right\|_{(\alpha ,k)}$ mit $k\in \mathbb {N} _{o}$ . Die untere Schranke $K_{(\alpha ,k)}\leq K_{\alpha }$ der Stetigkeitskonstanten für die einzelnen Quasihalbnormen $\left\|\cdot \right\|_{(\alpha ,k)}$ können dabei durchaus unterschiedlich sein. Man verlangt hier lediglich, dass einzelnen Stetigkeitskonstanten $K_{(\alpha ,k)}$ für die Sequenz nach oben durch $K_{\alpha }$ beschränkt sind.

p-Homogenität der p-Normen

Überträgt man die Argumentation der Stetigkeitskonstanten der Addition $K_{\alpha }$ auf ein Regularitätskriterium, dass über $p$ -Halbnormen definiert ist, so ergibt sich daraus, dass die $p$ -Homogenitätsexponenten $p_{(\alpha ,k)}$ von $\left\|\cdot \right\|_{(\alpha ,k)}$ eine untere Schranke $p_{\alpha }\leq p_{(\alpha ,k)}$ besitzen, wobei gilt:

\left\|\lambda \cdot x\right\|_{(\alpha ,k)}=|\lambda |^{p_{(\alpha ,k)}}\cdot \left\|x\right\|_{(\alpha ,k)}

Veranschaulichung

Algebraerweiterung $B$ von $A$ ist hier eine lokalkonvexe Algebra, die ein inverses Element $b=z^{-1}\in B$ zu einem gegebenen $z\in A$ enthält.

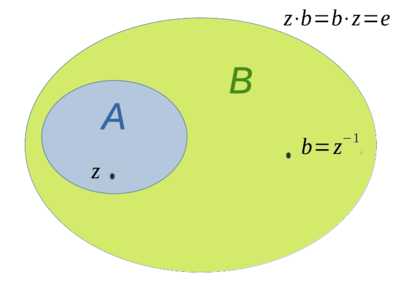
Pseudokonvexe Algebraerweiterung

Sei ${\textstyle {\mathcal {PC}}_{e}}$ die Klasse der pseudokonvex unitalen Algebren und ${\textstyle A\in {\mathcal {PC}}_{e}}$ . Die Algebraerweiterung ${\textstyle B\in {\mathcal {PC}}_{e}}$ bzw. ${\textstyle {\mathcal {PC}}}$ -Erweiterung von ${\textstyle A}$ benötigt nach Definition es einen Algebraisomorphismus ${\textstyle \tau :A\longrightarrow A'\subset B}$ mit:

${\textstyle \tau (e_{_{A}})=e_{_{B}}}$ , wobei ${\textstyle e_{_{A}}}$ ist das Einselement von ${\textstyle A}$ und ${\textstyle e_{_{B}}\in A'}$ das Einselement von ${\textstyle B}$ ist.
${\textstyle A}$ ist homöomorph zu ${\textstyle A'}$ ; d.h. ${\textstyle \tau }$ und ${\textstyle \tau ^{-1}:A'\longrightarrow A}$ sind stetig.

Veranschaulichung - Algebraisomorphismus

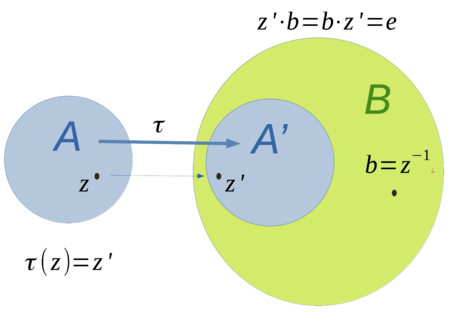
Algebraisomorphismus - Einbettung in die Algebraerweiterung

Im allgemeinen identifiziert man ${\textstyle A}$ mit ${\textstyle A'}$ und schreibt ${\textstyle A\subset B}$ . In der jeweiligen Konstruktion der Algebraerweiterung sieht man, dass die Element aus $x\in A$ mit Elementen $\tau (x)=x+I\in B$ in einem Quotientenraum $B:=A[t]/I$ identifiziert werden.
Sei ${\textstyle {\mathfrak {U}}_{A'}(0)}$ eine Nullumgebungsbasis der Relativtopologie von ${\textstyle B}$ auf ${\textstyle A'}$ und ${\textstyle {\mathfrak {U}}_{A}(0)}$ eine Nullumgebungsbasis von ${\textstyle A}$ , dann kann man die Homöomorphie zwischen ${\textstyle A}$ und ${\textstyle A'}$ wie immer über die Topologie ausdrücken:

{\begin{array}{rcl}\forall _{\displaystyle V\in {\mathfrak {U}}_{A}(0)}\exists _{\displaystyle U\in {\mathfrak {U}}_{A'}(0)}&:&U\subset V\,\,\,(\tau (U)\subset V)\\\forall _{\displaystyle U\in {\mathfrak {U}}_{A'}(0)}\exists _{\displaystyle V\in {\mathfrak {U}}_{A}(0)}&:&V\subset U\,\,\,(\tau ^{-1}(V)\subset U).\end{array}}

Stetigkeit über p-Halbnormen

Betrachtet man die p-Halbnormen ${\textstyle \left\|\cdot \right\|_{\widetilde {\mathcal {A}}}}$ und ${\textstyle \left\|\cdot \right\|_{\mathcal {A}}}$ für Nullumgebungen, so lassen sich die oberen beiden Aussagen wie folgt umformulieren (siehe auch Stetigkeitssatz für lineare Abbildungen):

{\begin{array}{rcl}\forall _{\alpha \in {\mathcal {A}}}\exists _{{\widetilde {\alpha }}\in {\widetilde {\mathcal {A}}},C_{1}>0}\forall _{x\in A}&:&\left\|x\right\|_{\alpha }\leq C_{1}\cdot \left\|\tau (x)\right\|_{\widetilde {\alpha }}\\{\mbox{ bzw. }}&&\left\|\cdot \right\|_{\alpha }\leq C_{1}\cdot \left\|\cdot \right\|_{\widetilde {\alpha }}\circ \tau \\\forall _{{\widetilde {\alpha }}\in {\mathcal {A}}}\exists _{\alpha \in {\mathcal {A}},C_{2}>0}\forall _{x\in A}&:&\left\|\tau (x)\right\|_{\widetilde {\alpha }}\leq C_{2}\cdot \left\|x\right\|_{\alpha }\\{\mbox{ bzw. }}&&\left\|\cdot \right\|_{\widetilde {\alpha }}\circ \tau \leq C_{2}\cdot \left\|\cdot \right\|_{\alpha }.\end{array}}

Wesentliche Schritte bei der Konstruktion der Algebraerweiterung

Wir betrachten zunächst kommutative Algebren $(A,\|\cdot \|_{A})$ .

Quasihalbnormensystem auf $A[t]$ definieren,
Hauptideal $I$ definieren,
Algebraerweiterung als Quotientenraum $B:=A[t]/I$ definieren.
Algebraische und topologische Eigenschafte auf $B$ nachweisen.

Quasihalbnormensystem

Ausgehend von $(A,\|\cdot \|_{A})$ wird die Polynomalgebra $(A[t],\|\!|\cdot |\!\|_{A[t]})$ mit einer Quasihalbnorm $\|\!|\cdot |\!\|_{A[t]}$ topologisiert.
Quasihalbnorm $\|\!|\cdot |\!\|_{A[t]}$ macht $A[t]$ zu einer topologischen Algebra, wobei die Stetigkeit der algebraischen Operationen (insbesondere die Stetigkeit der Cauchy-Multiplikation) nachzuweisen ist.

Hauptideal und Quotientenraum

Übergang zu dem Quotientenraum $B:=A[t]/I$ , wobei das Polynom $o(t):=z\cdot t-e_{A}$ das Hauptideal $I:=o\cdot A[t]$ definiert und $o\in A[t]$ ein Repräsentant des Nullvektors $0_{B}:=I=o+I$ in $B$ ist.

Die Konstruktion des Ideals $I$ liefert die algebraische Invertierbarkeit, denn mit $b(t):=e_{A}\cdot t$ ist $b_{I}:=b+I\in B=A[t]/I$ das inverse Element zu $z\in A$ mit $z_{I}:=\tau (z)=z+I\in B$ mit $z_{I}\cdot b_{I}-e_{B}=0_{B}$ bzw. $z_{I}\cdot b_{I}=e_{B}$ . Die Kommutativität liefert dann, dass auch $b_{I}\cdot z_{I}=e_{B}$ gilt.

Algebraerweiterung

Der Algebrahomomorphismus $\tau :A\to B$ bildet nun jedes Element $x\in A$ auf die Nebenklasse $x+I\in B:=A[t]/I$ ab. Dabei seien $A,B\in {\mathcal {PC}}_{e}^{k}(\mathbb {K} )$ kommutative unitale ${\mathcal {PC}}$ -Algebren über dem Körper $\mathbb {K}$ .

Abgeschlossenes Hauptideal in der Polynomalgebra

Für das gegebene $z\in A$ in der kommutativen pseudokonvexen topologische Algebren $(A,\|\cdot \|_{A})$ definiert man ein Polynom $o\in A[t]$ mit $o(t):=z\cdot t-e_{A}$ , wobei $e_{A}$ das Einselement der Multiplikation in $A$ ist. Als Ideal definiert man $I:={\overline {o\cdot A[t]}}$ als abgeschlossenes Hauptideal in $A[t]$ . Als Untervektorraum $I$ wäre der Quotientenraum auch ein Vektorraum. Die zusätzliche Eigenschaft des Ideals sorgt dafür, dass auch die Multiplikation auf dem Quotientenraum wohldefiniert ist.

Topologisierung der Polynomalgebra

Mit dem Korrespondenzsatz für p-Halbnormen und Quasihalbnormen wird die Topologie auf $A[t]$ über Stetigkeitssequenzen und Quasihalbnormen mit $\alpha \in {\mathcal {A}}$ erzeugt. Im Folgenden sind alle Gaugefunktionale homogen.

Topologische große Potenzen

Aus der Negation der Definition von topologisch kleinen Potenzen erhält man für ${\textstyle z\in {\mathcal {TGP}}(A)=A\setminus {\mathcal {TKP}}(A)}$ , dass es für alle $\alpha \in {\mathcal {A}}$ ein $\beta \in {\mathcal {A}}$ und Konstanten $D_{k}(\alpha )>0$ gibt, sodass für alle $x\in A$ gilt:

\left\|x\right\|_{\alpha }\leq D_{k}(\alpha )\cdot \left\|z^{k}\cdot x\right\|_{\beta }

(siehe topologisch große Potenzen)

Notation der Konstanten

Im Folgenden werden die Konstanten ${\textstyle D_{k}^{n}(\alpha )>0}$ wie folgt bzgl. der Stetigkeitssequenzen auf der Polynomalgebra $A[t]$ indiziert.

$n\in \mathbb {N} _{0}$ ist der Index der Quasihalbnorm bzw. des ${\mathcal {TGP}}$ -Gaugefunktionals auf $A[t]$ ,
$k\in \mathbb {N} _{0}$ ist der Koeffizientenindex der Polynome und bzgl. des ${\mathcal {TGP}}$ -Gaugefunktionals auf $A[t]$ der Index des Gaugefunktionals, das auf den $k$ -ten Koeffizienten $q_{k}\in A$ des Polynoms $q\in A[t]$ angewendet wird.

PC-Regularitätskriterium für n=0

Mit dem PC-Regularitätskriterium erhält man: Sei ${\textstyle \left(A,\left\|\cdot \right\|_{\mathcal {A}}\right)\in {\mathcal {K}}_{e}^{k}}$ , ${\textstyle z\in A}$ , dann ist $z\in A$ genau dann, wenn es für alle ${\textstyle \alpha \in {\mathcal {A}}}$ ein ${\textstyle \beta \in {\mathcal {A}}}$ und eine Folge von Quasihalbnormen ${\textstyle \left(\left\|\cdot \right\|_{(\alpha ,k)}\right)_{k\in \mathbb {N} _{0}}}$ mit der Stetigkeitskonstante der Addition $K_{\alpha }\geq 1$ , positiven Konstanten ${\textstyle D_{k}^{0}(\alpha )}$ gibt, für die gilt:

${\textstyle \left\|x\right\|_{\alpha }\leq \left\|x\right\|_{(0,k)}^{(\alpha )}\leq D_{k}^{0}(\alpha )\cdot \left\|x\right\|_{\beta }}$ für alle ${\textstyle x\in A}$ und ${\textstyle k\in \mathbb {N} _{0}}$ und
${\textstyle \left\|x\right\|_{(0,k)}^{(\alpha )}\leq \left\|zx\right\|_{(0,k+1)}^{(\alpha )}}$ für alle ${\textstyle x\in A}$ und ${\textstyle k\in \mathbb {N} _{0}}$ .

Quasihalbnormen - Korrespondenzsatz

Das erzeugende System von Gaugefunktionalen ${\textstyle \left(\left\|\cdot \right\|_{\alpha }\right)_{\alpha \in {\mathcal {A}}}}$ sind Quasihalbnormen und damit homogen und subadditiv mit Stetigkeitskonstante $K_{\alpha }\geq 1$ und $D_{k}^{0}(\alpha )\geq 1$ :

${\textstyle \left\|x\right\|_{\alpha }\leq \left\|x\right\|_{(0,k)}^{(\alpha )}\leq D_{k}^{0}(\alpha )\cdot \left\|x\right\|_{\beta }}$ für alle ${\textstyle x\in A}$ und ${\textstyle k\in \mathbb {N} _{0}}$ und
${\textstyle \left\|x\right\|_{(0,k)}^{(\alpha )}\leq \left\|zx\right\|_{(0,k+1)}^{(\alpha )}}$ für alle ${\textstyle x\in A}$ und ${\textstyle k\in \mathbb {N} _{0}}$ .
$\left\|x+y\right\|_{(0,k)}^{(\alpha )}\leq K_{(\alpha ,0)}\cdot \left(\left\|x\right\|_{(0,k)}^{(\alpha )}+\left\|y\right\|_{(0,k)}^{(\alpha )}\right)$ bzw.
$\left\|x+y\right\|_{\beta }\leq K_{\beta }\cdot \left(\left\|x\right\|_{\beta }+\left\|y\right\|_{\beta }\right)$ mit $K_{(\alpha ,0)},K_{\beta }\geq 1$ .

Anfang der Stetigkeitssequenz

Man definiert auf der Algebra induktiv eine Stetigkeitssequenz auf $A$ und auf $A[t]$ und man parallel zu $\|\!|\cdot |\!\|_{(\alpha ,0)}$ auch $\|\cdot \|_{0}^{(\alpha )}:=\|\cdot \|_{\beta }$ . Die erste Folge von Quasihalbnormen auf $A[t]$ mit einer Stetigkeitskonstanten $K_{\alpha }\geq 1$ wird direkt über das ${\mathcal {PC}}$ -Kriterium definiert mit $C_{k}(\alpha )=\max\{1,D_{k}(\alpha ),C_{k-1}(\alpha )\}$ für $k>0$ und $C_{0}^{0}(\alpha ):=\max\{1,D_{0}(\alpha )\}$ (siehe auch PC-Regularitätskriterium).

{\begin{array}{rcl}\|\!|p|\!\|_{(\alpha ,0)}&:=&\displaystyle \sum _{k=0}^{\infty }C_{k}^{0}(\alpha )\|p_{k}\|_{\beta }=\displaystyle \sum _{k=0}^{\infty }\underbrace {C_{k}^{0}(\alpha )} _{\geq D_{k}(\alpha )}\cdot \|p_{k}\|_{0}^{(\alpha )}\\&\geq &\displaystyle \sum _{k=0}^{\infty }D_{k}(\alpha )\cdot \|p_{k}\|_{0}^{(\alpha )}\\&\geq &\displaystyle \sum _{k=0}^{\infty }\|p_{k}\|_{(0,k)}^{(\alpha )}=\|\!|p|\!\|_{(\alpha ,0)}^{(z)}\\\end{array}}

Erste Quasihalbnorm der PC-Stetigkeitssequenz

Gleichzeitig zu der Folge von Quasihalbnormen auf $A[t]$ wird auch eine Sequenz von Quasihalbnormen definiert, die man über das ${\mathcal {PC}}$ -Regularitätskriterium erhält. Da die Folge in Abhängigkeit von einem konkreten $z\in {\mathcal {G}}_{\mathcal {PC}}(A)$ und einem beliebigen $\alpha \in {\mathcal {A}}$ abhängig sind, definiert man diese Gaugefunktionale

{\begin{array}{rcl}\|\!|p|\!\|_{(\alpha ,0)}^{(z)}&:=&\displaystyle \sum _{k=0}^{\infty }\|p_{k}\|_{k}^{(\alpha )}\,\,\,{\mbox{ mit}}\\p(t)&=&\displaystyle \sum _{k=0}^{\infty }p_{k}\cdot t^{k}\end{array}}

Abschätzung für erste PC-Quasihalbnorm

Für die ${\mathcal {PC}}$ -Quasihalbnorm und den topologieerzeugenden Quasihalbnormen auf $A[t]$ gilt folgende Abschätzung für $n=0$ :

{\begin{array}{rcl}\|\!|p|\!\|_{(\alpha ,n)}^{(z)}&=&\displaystyle \sum _{k=0}^{\infty }\underbrace {\|p_{k}\|_{(0,k)}^{(\alpha )}} _{\leq D_{k}^{0}(\alpha )\cdot \|p_{k}\|_{0}^{(\alpha )}}\\&\leq &\displaystyle \sum _{k=0}^{\infty }C_{k}^{0}(\alpha )\cdot \|p_{k}\|_{0}^{(\alpha )}=\|\!|p|\!\|_{(\alpha ,n)}\\\end{array}}

Für $n=0$ wurden daher für alle $k\in \mathbb {N} _{0}$ die Koeffizienten $C_{k}^{0}(\alpha )\geq D_{k}^{0}(\alpha )$ definieren.

Bedeutung der Abschätzung

Diese Abschätzung ist wesentlich, um

einerseits die Stetigkeit des Algebraisomorphismus $\tau :A\to A'\subset B$ bzw. $\tau ^{-1}:A'\to A$ nachzuweisen (siehe auch Elemente mit topologisch großen Potenzen) und
andererseits dürfen die Gaugefunktionale $\|\!|\cdot |\!\|_{n}^{(\alpha ,z)}$ auch keine feinere Topologie erzeugen, als das Quasihalbnormensystem der Quasihalbnormen $\|\!|\cdot |\!\|_{(\alpha ,n)}$ mit $\alpha \in {\mathcal {A}}$ und $n\in \mathbb {N} _{0}$ .

Induktive Definition des Stetigkeitssequenzen

Seien nun die Quasihalbnormen $\|\cdot \|_{n}^{(\alpha )}$ , $\|\!|\cdot |\!\|_{(\alpha ,n)}$ und das ${\mathcal {TGP}}$ -Gaugefunktional $\|\!|\cdot |\!\|_{n}^{(\alpha ,z)}$ bereits gegeben, dann definiert man die nächsten Quasihalbnormen und das ${\mathcal {TGP}}$ -Gaugefunktional über folgende beiden Lemmata:

Anwendung des PC-Regularitätskriteriums

Zu der gegebenen Quasihalbnormen $\|\cdot \|_{n}^{(\alpha )}$ kann man mit ${\mathcal {PC}}$ -Regularitätskriterium ein $\gamma \in {\mathcal {A}}$ , eine Folge von Gaugefunktionalen ${\textstyle \left(\left\|\cdot \right\|_{(n,k)}^{(\alpha )}\right)_{k\in \mathbb {N} _{0}}}$ mit positiven Konstanten ${\textstyle D_{k}^{n+1}(\alpha )}$ finden, für die gilt:

${\textstyle \left\|x\right\|_{n}^{(\alpha )}\leq \left\|x\right\|_{(n+1,k)}^{(\alpha )}\leq D_{k}^{n+1}(\alpha )\cdot \left\|x\right\|_{\gamma }}$ für alle ${\textstyle x\in A}$ und ${\textstyle k\in \mathbb {N} _{0}}$ und
${\textstyle \left\|x\right\|_{(n+1,k)}^{(\alpha )}\leq \left\|zx\right\|_{(n+1,k+1)}^{(\alpha )}}$ für alle ${\textstyle x\in A}$ und ${\textstyle k\in \mathbb {N} _{0}}$ .

Definition eine Stetigkeitssequenz der Multiplikation

Man definiert nun schon einmal $\|x\|_{n+1}^{(\alpha )}:=\left\|x\right\|_{\widehat {\gamma }}$ für alle $x\in A$ , wobei ${\widehat {\gamma }}\in {\mathcal {A}}$ mit der Stetigkeit der Multiplikation und dem Topologisierungslemma für Algebren so gewählt wurde, dass für alle $x,y\in A$ gilt:

\|x\cdot y\|_{\gamma }\leq \|x\|_{\widehat {\gamma }}\cdot \|y\|_{\widehat {\gamma }}

Damit erhält man eine Stetigkeitssequenz der Multiplikation mit:

\|x\cdot y\|_{n}^{(\alpha )}\leq \|x\|_{n+1}^{(\alpha )}\cdot \|y\|_{n+1}^{(\alpha )}

Anwendung - Koeffizientenlemma der Cauchy-Multiplikation

Nun definiert man über das Koeffizientenlemma der Cauchy-Multiplikation zunächst die Koeffizienten für die Quasihalbnormen der Stetigkeitssequenz, damit die Cauchy-Multiplikation auf $A[t]$ stetig wird. Bzgl. der topologischen Algebra $(A,\|\cdot \|_{\mathcal {A}})$ ist basiserzeugendes Quasihalbnormensystem $\|\cdot \|_{\mathcal {A}}$ gegeben aus dem die Halbnorm $\|\cdot \|_{n+1}^{(\alpha )}$ mit dem ${\mathcal {TGP}}$ -Regularitätskriterium gewählt wurde. Als ${\textstyle K_{(\alpha ,n+1)}:=\max\{K_{\gamma },K_{(\alpha ,n)}\}\geq 1}$ setzt man die Stetigkeitskonstante der Addition einer Quasihalbnorm $\|\cdot \|_{n+1}^{(\alpha )}:=\|\cdot \|_{\gamma }$ . Damit gilt u.a. ${\textstyle K_{(\alpha ,n+1)}\geq K_{(\alpha ,n)}}$ und

\|x+y\|_{n+1}^{(\alpha )}\leq K_{(\alpha ,n+1)}\cdot \left(\|x\|_{n+1}^{(\alpha )}+\|y\|_{n+1}^{(\alpha )}\right).

Wahl der Folgen - Koeffizientenlemma der Cauchy-Multiplikation

In dem Koeffizientenlemma der Cauchy-Multiplikation werden die beiden Folgen positiver Zahlen ${\textstyle (a_{k})_{k\in \mathbb {N} _{0}}}$ und ${\textstyle (d_{k})_{k\in \mathbb {N} _{0}}}$ genannt. Diese werden induktiv in Abhängigkeit von $n\in \mathbb {N} _{0}$ und $\alpha \in {\mathcal {A}}$ wie folgt gewählt:

${\textstyle (a_{k})_{k\in \mathbb {N} _{0}}:=(C_{k}^{n}(\alpha ))_{n\in \mathbb {N} _{0}}}$ (Koeffizienten der Quasihalbnorm $\|\!|\cdot |\!\|_{(\alpha ,n)}$ )
${\textstyle (d_{k})_{k\in \mathbb {N} _{0}}:=(\max\{C_{k}^{n}(\alpha )\cdot D_{k}^{n+1}(\alpha ),K_{(\alpha ,n+1)})_{n\in \mathbb {N} _{0}}}$ (positive Konstanten des ${\mathcal {PC}}$ -Regularitätskriterium )

Eigenschaften der resultierende Folge aus dem Koeffizientenlemma

Das Koeffizientenlemma der Cauchy-Multiplikation liefert nun eine Folge ${\textstyle \left(C_{k}^{n+1}(\alpha )\right)_{k\in \mathbb {N} _{0}}:=\left(b_{k}\right)_{k\in \mathbb {N} _{0}}}$ von positiven Zahlen, die folgende zwei Eigenschaften erfüllt:

(KL1) ${\textstyle C_{k}^{n+1}(\alpha )\geq C_{k}^{n}(\alpha )\cdot D_{k}^{n+1}(\alpha )}$ für alle ${\textstyle k\in \mathbb {N} _{0}}$
(KL2) ${\textstyle K_{(\alpha ,n)}^{i+j}\cdot C_{i+j}^{n}(\alpha )\leq C_{i}^{n+1}(\alpha )\cdot C_{j}^{n+1}(\alpha )}$ für alle ${\textstyle i,j\in \mathbb {N} _{0}}$ .

Induktive Definition der Quasihalbnormen

Man definiert auf der Algebra nun induktiv das nächste Element der Stetigkeitssequenz auf $A[t]$ mit:

{\begin{array}{rcl}\|\!|p|\!\|_{(\alpha ,n+1)}&=&\displaystyle \sum _{k=0}^{\infty }\underbrace {C_{k}^{n+1}(\alpha )} _{\geq C_{k}^{n}(\alpha )\cdot D_{k}^{n+1}(\alpha )}\cdot \|p_{k}\|_{n+1}^{(\alpha )}\end{array}}

Dabei genügen die Koeffizienten der Ungleichung $C_{k}^{n+1}(\alpha )\geq C_{k}^{n}(\alpha )\cdot D_{k}^{n+1}(\alpha )$ auch dem TGP-Regularitätskriterium.

Indukutive Definition der PC-Quasihalbnorm bzgl. z

Gleichzeitig zu der Quasihalbnormen $\|\!|\cdot |\!\|_{(\alpha ,n+1)}$ auf $A[t]$ wird nun auch die ${\mathcal {PC}}$ -Quasihalbnorm definiert, die man über das ${\mathcal {PC}}$ -Regularitätskriterium erhält.

{\begin{array}{rcl}\|\!|p|\!\|_{(\alpha ,n+1)}^{(z)}&:=&\displaystyle \sum _{k=0}^{\infty }C_{k}^{n}(\alpha )\cdot \|p_{k}\|_{(n+1,k)}^{(\alpha )}\,\,\,{\mbox{ mit}}\\p(t)&=&\displaystyle \sum _{k=0}^{\infty }p_{k}\cdot t^{k}\end{array}}

Abschätzung von PC-Quasihalbnorm in Stetigkeitssequenzen

Für die ${\mathcal {PC}}$ -Quasihalbnorm und den topologieerzeugenden Quasihalbnormen auf $A[t]$ gilt folgende Abschätzung:

{\begin{array}{rcl}\|\!|p|\!\|_{(\alpha ,n+1)}^{(z)}&=&\displaystyle \sum _{k=0}^{\infty }C_{k}^{n}(\alpha )\cdot \underbrace {\|p_{k}\|_{(n+1,k)}^{(\alpha )}} _{\leq D_{k}^{n+1}(\alpha )\cdot \|p_{k}\|_{n+1}^{(\alpha )}}\\&\leq &\displaystyle \sum _{k=0}^{\infty }\underbrace {C_{k}^{n}(\alpha )\cdot D_{k}^{n+1}(\alpha )} _{\leq C_{k}^{n+1}(\alpha )}\cdot \|p_{k}\|_{n+1}^{(\alpha )}\leq \|\!|p|\!\|_{(\alpha ,n+1)}\\\end{array}}

Für $n=0$ kann man für alle $k\in \mathbb {N} _{0}$ die Koeffizienten $C_{k}^{0}(\alpha ):=D_{k}^{0}(\alpha )$ definieren.

Subadditivität mit Stetigkeitskonstante

Das definierte Funktional $\|\!|\cdot |\!\|_{(\alpha ,n)}$ ist subadditiv mit Stetigkeitskonstante $K_{\alpha ,n)}\geq 1$ , denn

{\begin{array}{rcl}\|\!|p+q|\!\|_{(\alpha ,n)}&=&\displaystyle \sum _{k=0}^{\infty }C_{k}^{n}(\alpha )\cdot \|p_{k}+q_{k}\|_{n}^{(\alpha )}\\&\leq &\displaystyle \sum _{k=0}^{\infty }C_{k}^{n}(\alpha )\cdot K_{(\alpha ,n)}\cdot \left(\|p_{k}\|_{n}^{(\alpha )}+\|q_{k}\|_{n}^{(\alpha )}\right)\\&=&\displaystyle K_{(\alpha ,n)}\cdot \sum _{k=0}^{\infty }C_{k}^{n}(\alpha )\cdot \|p_{k}\|_{n}^{(\alpha )}+C_{k}^{n}(\alpha )\cdot \|q_{k}\|_{n}^{(\alpha )}\\&=&K_{(\alpha ,n)}\cdot \left(\|\!|p|\!\|_{(\alpha ,n)}+\|\!q|\!\|_{(\alpha ,n)}\right)\\\end{array}}

Stetigkeit der Cauchy-Multiplkation 1

Die Stetigkeit der Cauchy-Multiplikation in der Polynomalgebra kann man mit der PC-Stetigkeit des Cauchy-Produktes angewendet auf die Stetigkeitssequenz nachweisen.

{\begin{array}{rcl}q(t)&=&\displaystyle \sum _{k=0}^{\infty }q_{k}\cdot t^{k}&{\mbox{ bzw. }}&p(t)=\displaystyle \sum _{k=0}^{\infty }p_{k}\cdot t^{k}\end{array}}

Stetigkeit der Multiplikation - Polynomalgebra

Mit der Stetigkeit der Multiplikation auf $A$ und der Anwendung des Koeffizientenlemmas der Cauchy-Multiplikation erhält man die Stetigkeit der Multiplikation auf $A[t]$ :

{\begin{array}{rcl}\|\!|p\cdot q|\!\|_{(\alpha ,n)}&\leq &\displaystyle \sum _{k=0}^{\infty }C_{k}^{n}(\alpha )\cdot \left\|\sum _{i=0}^{k}p_{i}\cdot q_{k-i}\right\|_{n}^{(\alpha )}\\&\leq &\displaystyle \sum _{k=0}^{\infty }C_{k}^{n}(\alpha )\cdot K_{(\alpha ,n)}^{k}\cdot \sum _{i=0}^{k}\left\|p_{i}\cdot q_{k-i}\right\|_{n}^{(\alpha )}\\&\leq &\displaystyle \sum _{k=0}^{\infty }\sum _{i=0}^{k}\underbrace {C_{k}^{n}(\alpha )\cdot K_{(\alpha ,n)}^{k}} _{=C_{i}^{k}(\beta )\cdot C_{k-i}^{k}(\beta )}\cdot \left\|p_{i}\right\|_{n+1}^{(\alpha )}\cdot \left\|q_{k-i}\right\|_{n+1}^{(\alpha )}\\&=&\displaystyle \sum _{k=0}^{\infty }\sum _{i=0}^{k}C_{i}^{n+1}(\alpha )\cdot \left\|p_{k}\right\|_{n+1}^{(\alpha )}\cdot C_{k-i}^{n+1}(\alpha )\cdot \left\|q_{n-k}\right\|_{n+1}^{(\alpha )}\\&=&\|\!|p|\!\|_{(\alpha ,n+1)}\cdot \|\!|q|\!\|_{(\alpha ,n+1)}\end{array}}

Topologisierung der Algebraerweiterung

Die Algebraerweiterung wird mit induzierten Quasihalbnormen auf Quotientenraum über die oben definierten Stetigkeitsequenzen topologisiert, die wie folgt definiert ist:

\|q_{_{I}}\|_{n}^{(\alpha ,B)}:=\|q+I\|_{n}^{(\alpha ,B)}:=\displaystyle \inf _{r\in I}\|\!|q+r|\!\|_{n}^{(\alpha )}

Dabei bezeichnen man die Äquivalenzklassen von Polynomen in Kurzform mit $q_{I}\in B$ , wobei diese Mengen wie folgt definiert sind:

q_{_{I}}:=q+I:=\{q+r\,:\,r\in I\}

Man muss hier keine Linksnebenklassen und Rechtsnebenklassen unterscheiden, da die Addition im Vektorraum und die Multiplikation in ${\mathcal {PC}}^{k}$ -Algebren auch eine kommuntative Cauchy-Multiplikation auf der Polynomalgebra induzieren.

Stetigkeit Algebrahomomorphismus

Sei $x\in A$ beliebig gewählt, dann gilt für eine beliebige Quasihalbnorm $\|\cdot \|_{n}^{(\alpha ,B)}$ auf dem Quotientenraum $B:=A[t]/I$ die folgende Abschätzung

{\begin{array}{rcl}\|\tau (x)\|_{n}^{(\alpha ,B)}&=&\|x_{I}\|_{n}^{(\alpha ,B)}=\|x+I\|_{n}^{(\alpha ,B)}:=\displaystyle \inf _{r\in I}\|\!|x+r|\!\|_{n}^{(\alpha )}\\&\leq &\|\!|x+0_{A[t]}|\!\|_{n}^{(\alpha )}=C_{0}^{n}{(\alpha )}\cdot \|x\|_{n}^{(\alpha )}\end{array}}

Damit ist $\tau$ stetig (siehe Stetigkeitssatz für lineare Abbildungen).

Struktur der Polynome aus dem Ideal

Betrachten nun das Bild $\tau (A)\subset B$ von $\tau$ in $B$ . Sei nun $A'=\tau (A)=\{x_{I}\,:\,x_{I}=x+I=\tau (x)\}$ gegeben und man betrachtet die Abschätzung für ein beliebiges $q\in A[t]$ mit $r=o\cdot q\in I$ mit $o(t)=z\cdot t-e_{A}$ . Dabei gilt:

{\begin{array}{rcl}r(t)&=&\displaystyle \sum _{k=0}^{\infty }r_{k}\cdot t^{k}=o(t)\cdot q(t)\\&=&-q_{0}+\sum _{k=1}^{\infty }(z\cdot q_{k-1}-q_{k})\cdot t^{k}\end{array}}

Injektivität des Algebrahomomorphismus 1

Um eine Umkehrabbildung von $\tau ^{-1}:A'\to A$ definieren zu können, muss man zeigen, dass $\tau :A\to A'\subset B$ injektiv ist, bzw. $Kern(\tau )=\{0_{A}\}$ . Wir zeigen nun die Kontraposition von der Implikation für die Injektivität

x\in Kern(\tau )\Longrightarrow x=0_{A}

und zeigen

x\not =0_{A}\Longrightarrow x\notin Kern(\tau ){\mbox{ bzw. }}\tau (x)\not =0_{B}

Injektivität des Algebrahomomorphismus 2

Sei $x\not =0_{A}$ und mit der Hausdorff-Eigenschaft von $(A,\|\cdot \|_{\mathcal {A}})$ erhält man ein $\alpha \in {\mathcal {A}}$ mit $\varepsilon :=\|x\|_{\alpha }>0$ und verwendet ferner folgende Abschätzungen für Quasinormen und das ${\mathcal {PC}}$ -Regularitätskriterium:

$\|x-y\|_{(0,k)}^{(\alpha )}\geq {\frac {1}{K_{\alpha }}}\cdot \|x\|_{(0,k)}^{(\alpha )}-\|y\|_{(0,k)}^{(\alpha )}$
$\|x\|_{(0,k)}^{(\alpha )}\leq \|z\cdot x\|_{(0,k+1)}^{(\alpha )}$

Injektivität des Algebrahomomorphismus 3

{\begin{array}{l}\|\!|x+r|\!\|_{(\alpha ,0)}\geq \|\!|x+r|\!\|_{0}^{(\alpha ,z)}=\\=D_{0}^{0}(\alpha )\cdot \|x-q_{0}\|_{(0,k)}^{(\alpha )}+\sum _{k=1}^{\infty }K_{(\alpha ,0)}^{k}\cdot D_{k}^{0}(\alpha )\cdot \|z\cdot q_{k-1}-q_{k}\|_{(0,k)}^{(\alpha )}\\\\\geq \|x-q_{0}\|_{(0,k)}^{(\alpha )}+\sum _{k=1}^{\infty }K_{(\alpha ,0)}^{k-1}\left(\|z\cdot q_{k-1}\|_{(0,k)}^{(\alpha )}-K_{(\alpha ,0)}^{k}\|q_{k}\|_{(0,k)}^{(\alpha )}\right)\\\\\geq \|x-q_{0}\|_{(0,k)}^{(\alpha )}+\sum _{k=1}^{\infty }K_{(\alpha ,0)}^{k-1}\cdot \|q_{k-1}\|_{(0,k-1)}^{(\alpha )}-K_{(\alpha ,0)}^{k}\cdot \|q_{k}\|_{(0,k)}^{(\alpha )}\\\\\geq \|x-q_{0}\|_{(0,k)}^{(\alpha )}+\|q_{0}\|_{(0,k)}^{(\alpha )}\geq {\frac {1}{K_{(\alpha ,0)}}}\|x\|_{0}^{(\alpha )}\geq {\frac {\varepsilon }{K_{(\alpha ,0)}}}>0\end{array}}

Injektivität Algebrahomomorphismus 4

Über Infimumbildung über alle $r\in I$ bleibt die Ungleichung erhalten und es gilt:

\|x_{_{I}}\|_{0}^{(\alpha ,B)}:=\|x+I\|_{0}^{(\alpha ,B)}:=\displaystyle \inf _{r\in I}\|\!|x+r|\!\|_{0}^{(\alpha )}\geq {\frac {1}{K_{(\alpha ,0)}}}\|x\|_{\alpha }>0

Damit gilt auch $x_{_{I}}\not =0_{B}=0_{A}+I$ für $x\not =0_{A}$ . Damit ist der Algebrahomomophismus injektiv.

Existenz der Umkehrabbildung

Mit der Injektivität von $\tau :A\to A'\subset B$ existiert die Umkehrabbildung von $\tau ^{-1}:A'\to A$ und man kann die Stetigkeit der Umkehrabbildung mit der Stetigkeitssequenzen analog zur Injektivität für beliebige $n\in \mathbb {N} _{0}$ und $\alpha \in {\mathcal {A}}$ -

Stetigkeit der Umkehrabbildung der Einbettung

{\begin{array}{l}\|\!|x+r|\!\|_{(\alpha ,n+1)}\geq \|\!|x+r|\!\|_{n+1}^{(\alpha ,z)}=\\\geq D_{0}^{n+1}(\alpha )\cdot \|x-q_{0}\|_{(n,k)}^{(\alpha )}+\sum _{k=1}^{\infty }K_{(\alpha ,n)}^{k}\cdot D_{k}^{n}(\alpha )\cdot \|z\cdot q_{k-1}-q_{k}\|_{(n+1,k)}^{(\alpha )}\\\\=\|x-q_{0}\|_{n}^{(\alpha )}+\sum _{k=1}^{\infty }K_{(\alpha ,n)}^{k}\cdot \|z\cdot q_{k-1}-q_{k}\|_{n}^{(\alpha )}\\\\\geq \|x-q_{0}\|_{n}^{(\alpha )}+\sum _{k=1}^{\infty }K_{(\alpha ,n)}^{k-1}\|z\cdot q_{k-1}\|_{(n,k)}^{(\alpha )}-K_{(\alpha ,n)}^{k}\|q_{k}\|_{(n,k)}^{(\alpha )}\\\\\geq \|x-q_{0}\|_{(n,k)}^{(\alpha )}+\sum _{k=1}^{\infty }K_{(\alpha ,n)}^{k-1}\cdot \|q_{k-1}\|_{(n,k-1)}^{(\alpha )}-K_{(\alpha ,n)}^{k}\cdot \|q_{k}\|_{(n,k)}^{(\alpha )}\\\\\geq \|x-q_{0}\|_{(n,k)}^{(\alpha )}+\|q_{0}\|_{(n,k)}^{(\alpha )}\geq {\frac {1}{K_{(\alpha ,n)}}}\|x\|_{n}^{(\alpha )}\end{array}}

Begründungen für die Umformungen

(1. Gleichungszeile) $\|\!|q|\!\|_{(\alpha ,n)}\geq \|\!|q|\!\|_{n}^{(\alpha ,z)}$ gilt für alle $q\in A[t]$
(2. Gleichungszeile) Definition von $\|\!|q|\!\|_{n}^{(\alpha ,z)}$ für $q\in A[t]$ eingesetzt,
(3. Gleichungszeile) $D_{n}^{k}(\alpha )\geq 1$ für alle $k\in \mathbb {N} _{0}$ verwendet,

(4. Gleichungszeile)
(2. Gleichungszeile)

Teleskopierende Summen

Bei teleskopierenden Summen werden Summen betrachtet, wobei die Summanden selbst Differenzen sind. Aufeinanderfolgende Teilterme heben sich dabei auf. In der obigen Abschätzung bilden die Terme

K_{(\alpha ,n)}^{k-1}\cdot \|q_{k-1}\|_{(n,k-1)}^{(\alpha )}-K_{(\alpha ,n)}^{k}\cdot \|q_{k}\|_{(n,k)}^{(\alpha )}

eine Telekopsumme.

Infimumbildung

Durch Infimumbildung über alle Polynome $r\in I$ bleibt die obige Ungleichung erhalten und man erhält die Stetigkeit von $\tau ^{-1}:A'\to A$ .

{\begin{array}{rcl}\|x+I\|_{(\alpha ,n)}&=&\displaystyle \inf _{r\in I}\|\!|x+r|\!\|_{(\alpha ,n)}\geq {\frac {1}{K_{(\alpha ,n)}}}\cdot \|x\|_{n}^{(\alpha )}\\&\geq &{\frac {1}{K_{(\alpha ,n)}}}\cdot \|\tau ^{-1}(x+I)\|_{n}^{(\alpha )}\end{array}}

Die Stetigkeit $\|\tau ^{-1}(x+I)\|_{n}^{(\alpha )}\leq \underbrace {K_{(\alpha ,n)}} _{:=C_{1}>0}\cdot \|x+I\|_{(\alpha ,n)}$ erhält man mit dem Stetigkeitssatz für lineare Abbildungen.

Umgekehrte Abschätzung

Für die Stetigkeit der Abbildung $\tau$ gibt es für alle $\alpha \in {\mathcal {A}}$ und alle $n\in \mathbb {N} _{0}$ setzt das Nullpolynom $0_{A[t]}\in I$ ein:

\|x+I\|_{(\alpha ,n)}:=\displaystyle \inf _{r\in I}\|\!|x+r|\!\|_{(\alpha ,n)}\leq \|\!|x+0_{A[t]}|\!\|_{(\alpha ,n)}=\underbrace {C_{0}^{n}(\alpha )} _{=C_{2}>0}\cdot \|x\|_{n}^{(\alpha )}

Insgesamt ist der Algebraisomorphismus der Einbettung von $A$ in $A'\subset B:=A[t]/I$ eine Hömöomorphismus mit $\tau ^{-1}(x+I)=x$ bzw. $\tau (x)=x+I$ .

Aufgabe - Algebraisomorphismus und Äquivalenz von p-Halbnormensystemen

In den obigen beiden Abschätzungen wird die Stetigkeit von lineare Abbildung bzw. von Algebrahomomorphismen verwendet, um die Stetigkeit von $\tau$ und $\tau ^{-1}$ über Quasihalbnormen auszudrücken. Wir betrachten nun zwei Quasihalbnormensysteme $\|\cdot \|_{\mathcal {A}}$ auf $A$ und $\|\!|\cdot |\!\|_{{\mathcal {A}}\times \mathbb {N} _{0}}$ auf $A[t]$ und definieren eine weiteres Halbnormensystem $\|\!|\cdot |\!\|_{{\mathcal {A}}\times \mathbb {N} _{0}}^{(\tau _{3})}$ auf $A$ mit

\|\!|\cdot |\!\|_{(\alpha ,n)}^{(\tau _{3})}:=\|\!|\cdot |\!\|_{(\alpha ,n)}\circ \tau _{3}{\mbox{ bzw. }}\|\!|x|\!\|_{(\alpha ,n)}^{(\tau _{3})}:=\|\!|\tau _{3}(x)|\!\|_{(\alpha ,n)}

Dabei wird $\tau _{3}(x)=p\in A[t]$ mit $p(t)=x\cdot t^{0}$ . Zeigen Sie, dass $p$ -Halbnormensysteme $\|\cdot \|_{\mathcal {A}}$ und $\|\!|\cdot |\!\|_{{\mathcal {A}}\times \mathbb {N} _{0}}^{(\tau _{3})}$ auf $A$ äquivalente Quasihalbnormensysteme sind (siehe Äquivalenz (Gaugefunktionalsysteme)).

Quellennachweise

↑ Zelazko Wieslaw, (1984), Concerning characterization of permanently sin- gular elements in commutative locally convex algebras, Mathematical Structures – Computational Mathematics – Mathematical Modelling 2, Sofia, S. 326-333;
↑ Andreas Rohling, Niehaus Engelbert (1995) Verallgemeinerung des Satzes von Gleason-Kahane-Zelazko, K-reguläre Elemente, Schriftenreihe des Mathematischen Instituts der Universität Münster, Serie 3., Herausgeber: George Maltese, Heft 16, S. 79-81

Siehe auch

Seiteninformation

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Topologische Invertierbarkeitskriterien' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Topologische%20Invertierbarkeitskriterien/PC-Regularit%C3%A4t
siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.

[1] Zelazko Wieslaw, (1984), Concerning characterization of permanently sin- gular elements in commutative locally convex algebras, Mathematical Structures – Computational Mathematics – Mathematical Modelling 2, Sofia, S. 326-333;

[2] Andreas Rohling, Niehaus Engelbert (1995) Verallgemeinerung des Satzes von Gleason-Kahane-Zelazko, K-reguläre Elemente, Schriftenreihe des Mathematischen Instituts der Universität Münster, Serie 3., Herausgeber: George Maltese, Heft 16, S. 79-81

[1]

[2]