Kurs:Vorkurs Mathematik (Osnabrück 2009)/Vorlesung 5

Verknüpfungen

Die Addition und die Multiplikation auf den natürlichen Zahlen und die Hintereinanderschaltung von Abbildungen auf einer Menge sind wichtige Beispiele für das Konzept der Verknüpfung.

Definition

Eine Verknüpfung ${}\circ$ auf einer Menge ${}M$ ist eine Abbildung

$\circ \colon M\times M\longrightarrow M,\,(x,y)\longmapsto \circ (x,y)=x\circ y.$

Eine Verknüpfung macht also aus einem Paar

${}(x,y)\in M\times M\,$

ein einziges Element

${}x\circ y\in M\,.$

Eine Vielzahl von mathematischen Konstruktionen fällt unter diesen Begriff: Die Addition, die Differenz, die Multiplikation, die Division von Zahlen, die Verknüpfung von Abbildungen, der Durchschnitt oder die Vereinigung von Mengen, etc. Als Verknüpfungssymbol kommt eine ganze Reihe in Frage, z.B. ${}\circ ,\cdot ,+,-,\oplus ,\clubsuit ,\heartsuit$ u.s.w. Je nach dem gewählten Symbol spricht man statt Verknüpfung auch von Multiplikation oder Addition, ohne dass man damit eine inhaltliche Bedeutung verbinden sollte. Wichtige strukturelle Eigenschaften einer Verknüpfung werden in den folgenden Definitionen aufgelistet.

Definition

Eine Verknüpfung

$\circ \colon M\times M\longrightarrow M,\,(x,y)\longmapsto x\circ y,$

auf einer Menge ${}M$ heißt kommutativ, wenn für alle ${}x,y\in M$ die Gleichheit

${}x\circ y=y\circ x\,$

gilt.

Definition

Eine Verknüpfung

$\circ \colon M\times M\longrightarrow M,\,(x,y)\longmapsto x\circ y,$

auf einer Menge ${}M$ heißt assoziativ, wenn für alle ${}x,y,z\in M$ die Gleichheit

${}(x\circ y)\circ z=x\circ (y\circ z)\,$

gilt.

Definition

Es sei eine Menge ${}M$ mit einer Verknüpfung

$\circ \colon M\times M\longrightarrow M,\,(x,y)\longmapsto x\circ y,$

gegeben. Dann heißt ein Element ${}e\in M$ neutrales Element der Verknüpfung, wenn für alle ${}x\in M$ die Gleichheit ${}x\circ e=x=e\circ x$ gilt.

Im kommutativen Fall muss man natürlich für das neutrale Element nur eine Reihenfolge betrachten.

Definition

Es sei eine Menge ${}M$ mit einer Verknüpfung

$\circ \colon M\times M\longrightarrow M,\,(x,y)\longmapsto x\circ y,$

und einem neutralen Element ${}e\in M$ gegeben. Dann heißt zu einem Element ${}x\in M$ ein Element ${}y\in M$ inverses Element (zu ${}x$). wenn die Gleichheit

${}x\circ y=e=y\circ x\,$

gilt.

Bei einer Verknüpfung auf einer Menge ${}M$ bezeichnet man eine (vollständige) Wertetabelle auch als Verknüpfungstafel. In einer solchen Tabelle stehen sowohl in der Leitzeile als auch in der Leitspalte die (linear geordneten) Elemente aus ${}M$, und in der Überkreuzungsstelle zu ${}x$ und ${}y$ steht der Verknüpfungswert ${}x\circ y$ als Eintrag. Dabei muss man festlegen, welche Ordnung zwischen den Zeilen und Spalten gilt, also ob im Kreuzungspunkt der ${}x$-ten Spalte und der ${}y$-ten Zeile ${}x\circ y$ oder ${}y\circ x$ steht. Diese Festlegung ist insbesondere wichtig, da bei Matrizen und Koordinatensystemen andere Konventionen gelten.

Die Peano-Axiome

In den natürlichen Zahlen ${}\mathbb {N}$ kann man addieren, multiplizieren, potenzieren, teilweise abziehen, es gibt die kleiner/gleich-Relation, die Teilbarkeit, usw. Man kann sich nun fragen, welche Abhängigkeiten zwischen diesen mathematischen Strukturen bestehen und ob man manche davon auf andere, grundlegendere Strukturen zurückführen kann. Dies führt zum axiomatischen Aufbau der natürlichen Zahlen.

Giuseppe Peano (1858 -1932)

Definition

Eine Menge ${}N$ mit einem ausgezeichneten Element ${}0\in N$ (die Null) und einer (Nachfolger)-Abbildung

$'\colon N\longrightarrow N,\,n\longmapsto n',$

heißt natürliche Zahlen (oder Dedekind-Peano-Modell für die natürlichen Zahlen), wenn die folgenden Dedekind-Peano-Axiome erfüllt sind.

1. Das Element ${}0$ ist kein Nachfolger (die Null liegt also nicht im Bild der Nachfolgerabbildung).
2. Jedes ${}n\in N$ ist Nachfolger höchstens eines Elementes (d.h. die Nachfolgerabbildung ist injektiv).
3. Für jede Teilmenge ${}T\subseteq N$ gilt: Wenn die beiden Eigenschaften
   • ${}0\in T$,
   • mit jedem Element
   ${}n\in T$ ist auch ${}n'\in T$,

gelten, so ist ${}T=N$.

Das heißt, dass die natürlichen Zahlen durch das natürliche Zählen bestimmt sind. Zählen heißt, von einem Startwert ausgehend, nach und nach einen Schritt (einen Strich machen, einen Stab dazulegen, einen Punkt dazumalen) weiterzuzählen. Das „Weiter“-Zählen ist also fundamentaler als eine bestimmte Benennung von Zahlen. Eine natürliche Zahl repräsentiert, wie oft bis zu ihr gezählt werden musste. Die erste Eigenschaft legt den Start fest. Die zweite Eigenschaft besagt, dass wenn zwei Zahlen verschieden sind (oder zwei endliche Mengen mit unterschiedlicher Anzahl vorliegen), dann auch die beiden jeweiligen Nachfolger verschieden sind (die beiden jeweils um ein neues Element erweiterten Mengen ebenfalls eine unterschiedliche Anzahl haben). Die dritte Eigenschaft, die man auch das Induktionsprinzip für Mengen nennt, besagt, dass wenn man bei null anfängt und keinen einzelnen Zählvorgang auslässt, dass man dann vollständig alle natürlichen Zahlen abzählt.

Es sei erwähnt, dass solche Überlegungen, die natürlichen Zahlen grundlegend zu begründen, manchmal eher verwirrend als hilfreich sein können. Bei den natürlichen Zahlen ist es erfahrungsgemäß nicht gefährlich, der Intuition zu vertrauen und mit einer naiven Vorstellung davon zu arbeiten (dies gilt für die reellen Zahlen nicht in dieser Deutlichkeit). Das ist beim Studienanfang jedenfalls wichtiger als Grundlagenfragen.

Ausgehend von den Peano-Axiomen kann man eine Addition auf der Menge der natürlichen Zahlen definieren, wobei die Nachfolgefunktion der Addition mit ${}1=0'$ entspricht. Die Definierbarkeit beruht selbst auf dem Induktionsprinzip. Ebenso kann man eine Multiplikation definieren und die üblichen Eigenschaften wie Kommutativität und Assoziativität nachweisen.

Wir werden im Folgenden von einem Modell der natürlichen Zahlen ausgehen, bei dem bereits eine Addition und eine Multiplikation definiert wurde, und wir werden die übliche Zifferndarstellung für natürliche Zahlen (im Zehnersystem) verwenden. Wir schreiben also

$\mathbb {N} =\{0,0',(0')',((0')')',\ldots \}=\{0,1,2,3,4,\ldots \}$

und sprechen von der Menge der natürlichen Zahlen. Des weiteren werden wir die lineare (totale) Ordnung auf ${}\mathbb {N}$ benutzen, wobei ${}x\leq y$ bedeutet, dass es ein ${}z\in \mathbb {N}$ gibt mit ${}y=x+z$.

Das Induktionsprinzip für Aussagen

Die folgende Aussage und ihr Beweis begründen das Beweisprinzip der vollständigen Induktion.

Satz

Für jede natürliche Zahl ${}n$ sei eine Aussage ${}A(n)$ gegeben. Es gelte

1. ${}A(0)$ ist wahr.
2. Für alle ${}n$ gilt: wenn ${}A(n)$ gilt, so ist auch ${}A(n+1)$ wahr.

Dann gilt ${}A(n)$ für alle ${}n$.

Beweis

Es sei

${}M={\left\{n\in \mathbb {N} \mid A(n){\text{ ist wahr}}\right\}}\,.$

Wir wollen zeigen, dass ${}M=\mathbb {N}$ ist, denn genau dies bedeutet, dass die Aussage für alle ${}n$ gilt. Nach der ersten Bedingung ist

${}0\in M\,.$

Nach der zweiten Voraussetzung gilt für ${}M$, dass aus ${}n\in M$ stets ${}n+1\in M$ folgt. Damit erfüllt ${}M$ beide Voraussetzungen im Induktionsprinzip für Mengen, sodass ${}M=\mathbb {N}$ gilt.

$\Box$

Aus dem Induktionsprinzip folgt die nächste wichtige Eigenschaft. Vom intuitiven Standpunkt her ist sie selbstverständlich, wir führen sie aber trotzdem auf das Induktionsprinzip zurück. Es geht in diesem Beweis weniger dadrum, sich über die Satzaussage zu vergewissern, sondern vielmehr Einblicke in mathematisches Argumentieren zu gewinnen. Es ist auch ein Beispiel dafür, wie man eine Aussage über Teilmengen zu einer Aussage über natürliche Zahlen macht, um das Induktionsprinzip anwenden zu können.

Lemma

Jede nichtleere Teilmenge ${}M\subseteq \mathbb {N}$

besitzt ein Minimum.

Beweis

Wir betrachten die Aussage

${}A(n)$ = Alle Teilmengen von ${}\mathbb {N}$, die ${}n$ enthalten, besitzen ein Minimum.

Da jede nichtleere Teilmenge mindestens ein ${}n\in \mathbb {N}$ besitzt, ist die Aussage des Satzes äquivalent zur Gültigkeit von ${}A(n)$ für alle ${}n$. Diese Aussage können wir durch Induktion beweisen. Die Aussage ${}A(0)$ besagt, dass jede Teilmenge ${}M\subseteq \mathbb {N}$, die die ${}0$ enthält, auch ein Minimum enthält. Dies ist aber klar, da dann eben ${}0$ das Minimum ist. Es sei die Aussage ${}A(k)$ nun für alle ${}k\leq n$ schon bewiesen. Wir müssen ${}A(n+1)$ beweisen. Es sei also ${}M\subseteq \mathbb {N}$ eine Teilmenge, die ${}n+1$ enthält. Wenn ${}M$ auch eine Zahl ${}k<n+1$ besitzt, so besitzt ${}M$ nach der Induktionsvoraussetzung ein Minimum. Andernfalls besitzt ${}M$ keine Zahl, die kleiner als ${}n+1$ ist. Dann ist aber ${}n+1$ das Minimum von ${}M$.

$\Box$

Fakultät und Binomialkoeffizienten

Es seien nun ${}a_{i}$, ${}i=1,\ldots ,n$, (${}n\geq 1$) reelle Zahlen (oder Elemente in einem Körper, ein Begriff, den wir bald einführen werden). Dann wird das Summen- und das Produktzeichen folgendermaßen definiert.

$\sum _{i=1}^{n}a_{i}=a_{1}+a_{2}+\cdots +a_{n}{\text{ und }}\prod _{i=1}^{n}a_{i}=a_{1}\cdot a_{2}{\cdots }a_{n}.$

Dies sind geschlossene und einfach zu verstehende Ausdrücke. Formal korrekter und auch beweistechnisch vorteilhaft ist es, diese Zeichen induktiv durch

$\sum _{i=1}^{n}a_{i}=(\sum _{i=1}^{n-1}a_{i})+a_{n}{\text{ und }}\prod _{i=1}^{n}a_{i}=(\prod _{i=1}^{n-1}a_{i})a_{n}$

zu erklären. Insbesondere sind für ${}n\in \mathbb {N}$ die Vielfachen durch

$na=\sum _{i=1}^{n}a=(n-1)a+a=\underbrace {a+a+\cdots +a} _{n{\text{-mal}}}$

und die Potenzen durch

$a^{n}=\prod _{i=1}^{n}a=a^{n-1}\cdot a=\underbrace {a\cdot a{\cdots }a} _{n{\text{-mal}}}$

definiert. Dabei gelten die Konventionen ${}0a=0$ und ${}a^{0}=1$ (die erste lässt sich auch über die Multiplikation begründen, die zweite ist aber auch sinnvoll).

Definition

Zu einer natürlichen Zahl ${}n$ nennt man die Zahl

${}n!:=n(n-1)(n-2)\cdots 3\cdot 2\cdot 1\,$

die Fakultät von ${}n$ (sprich ${}n$ Fakultät).

Bei einer ${}n$-elementigen Menge ${}M$ gibt es ${}n!$ bijektive Abbildungen von ${}M$ nach ${}M$. Gleichbedeutend damit ist, dass es ${}n!$ Möglichkeiten, ${}n$ Objekte auf ${}n$ Plätze zu verteilen.

Definition

Es seien ${}k$ und ${}n$ natürliche Zahlen mit ${}k\leq n$. Dann nennt man

${}{\binom {n}{k}}:={\frac {n!}{k!(n-k)!}}\,$

den Binomialkoeffizienten „${}n$ über ${}k$ “.

Von dieser Definition her ist es nicht sofort klar, dass es sich dabei um natürliche Zahlen handelt. Dies folgt aus der folgenden Beziehung.

Das Dreieck der Binomialkoeffizienten war in Indien und in Persien schon um 1000 bekannt,

in China heißt es Yanghui-Dreieck (nach Yang Hui (um 1238-1298)),

in Europa heißt es das Pascalsche Dreieck (nach Blaise Pascal (1623-1662)).

Lemma

Die Binomialkoeffizienten

erfüllen die rekursive Beziehung

${}{\binom {n+1}{k}}={\binom {n}{k}}+{\binom {n}{k-1}}\,.$

Beweis

Siehe Aufgabe 5.21.

$\Box$

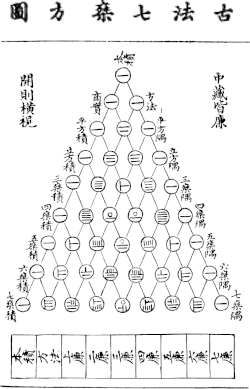
Die folgende Formel bringt die Addition und die Multiplikation miteinander in Beziehung.

Satz (Binomi)  

Es seien ${}a,b$ reelle (oder ganze)

Zahlen. Ferner sei ${}n$ eine natürliche Zahl. Dann gilt

$(a+b)^{n}=\sum _{k=0}^{n}{\binom {n}{k}}a^{k}b^{n-k}.$

Beweis  

Wir führen Induktion nach ${}n$. Für ${}n=0$ steht einerseits ${}(a+b)^{0}=1$ und andererseits ${}a^{0}b^{0}=1$. Es sei die Aussage bereits für ${}n$ bewiesen. Dann ist

${}{\begin{aligned}(a+b)^{n+1}&=(a+b)(a+b)^{n}\\&=(a+b){\left(\sum _{k=0}^{n}{\binom {n}{k}}a^{k}b^{n-k}\right)}\\&=a\left(\sum _{k=0}^{n}{\binom {n}{k}}a^{k}b^{n-k}\right)+b\left(\sum _{k=0}^{n}{\binom {n}{k}}a^{k}b^{n-k}\right)\\&=\sum _{k=0}^{n}{\binom {n}{k}}a^{k+1}b^{n-k}+\sum _{k=0}^{n}{\binom {n}{k}}a^{k}b^{n-k+1}\\&=\sum _{k=1}^{n+1}{\binom {n}{k-1}}a^{k}b^{n-k+1}+\sum _{k=0}^{n+1}{\binom {n}{k}}a^{k}b^{n-k+1}\\&=\sum _{k=1}^{n+1}\left({\binom {n}{k-1}}+{\binom {n}{k}}\right)a^{k}b^{n+1-k}+b^{n+1}\\&=\sum _{k=1}^{n+1}{\binom {n+1}{k}}a^{k}b^{n+1-k}+b^{n+1}\\&=\sum _{k=0}^{n+1}{\binom {n+1}{k}}a^{k}b^{n+1-k}.\end{aligned}}$

$\Box$

Fußnoten

<< | Kurs:Vorkurs Mathematik (Osnabrück 2009) | >> PDF-Version dieser Vorlesung Arbeitsblatt zur Vorlesung (PDF)