Kurs:Topologische Invertierbarkeitskriterien/MLC-Regularität

Einführung

Wenn wir die ${\mathcal {MLC}}$-Regularität eines Elementes $z\in A$ für eine multiplikativ lokalkonvexe topologische Algebra $(A,\|\cdot \|_{\mathcal {A}})$ sprechen, suchen wir nach einer multiplikativ lokalkonvexen Algebraerweiterungen $(B,\|\cdot \|_{\widetilde {\mathcal {A}}})$ von $(A,\|\cdot \|_{\mathcal {A}})$ in der $z\in A$ invertierbar ist. Dabei besteht

• $\|\cdot \|_{\mathcal {A}}:=\{\|\cdot \|_{\alpha }\,:\,\alpha \in {\mathcal {A}}\}$ und
• $\|\cdot \|_{\widetilde {\mathcal {A}}}:=\{\|\cdot \|_{\widetilde {\alpha }}\,:\,{\widetilde {\alpha }}\in {\widetilde {\mathcal {A}}}\}$

aus einem System von submultiplikativen Halbnormen, die die Topologie auf $A$ bzw. $B$ erzeugen.

Zielsetzung

Zielsetzung einer multiplikativ lokalkonvexe Algebraerweiterung $(B,\|\cdot \|_{\widetilde {\mathcal {A}}})$ zu einer gegebenen topologischen Algebra $(A,\|\cdot \|_{\mathcal {A}})$ mit $z\in A$ ist es, die gegebene multiplikativ lokalkonvexe Algebraerweiterung so zu vergrößern, dass diese ein inverses Element $z^{-1}:=b\in B$ in der multiplikativ lokalkonvexen Algebraerweiterung $B$ besitzt. Als topologieerzeugende $p$-Gaugefunktionale werden hier Halbnormensystem $\|\cdot \|_{\mathcal {A}}$ und $\|\cdot \|_{\widetilde {\mathcal {A}}}$ verwendet.

Charakterisierung der MLC-Regularität

Für kommutative multiplikativ lokalkonvexe Algebren $(A,\|\cdot \|_{\mathcal {A}})$ mit unital positivem System von erhält man folgende Charakterisierung:

• $z\in A$ ${\mathcal {MLC_{e}^{k}}}$-singulär $\Longleftrightarrow$ $z\in {\mathcal {MTNT}}(A)$ (multiplikativer topologischer Nullteiler)
• $z\in A$ ${\mathcal {MLC_{e}^{k}}}$-regulär $\Longleftrightarrow$ für alle $\alpha \in {\mathcal {A}}$ und ein $D_{\alpha }>0$ mit $\|x\|_{\alpha }\leq D_{\alpha }\cdot \|z\cdot x\|_{\alpha }$ für alle $x\in A$

Dabei sind $\|\cdot \|_{\alpha }$ submultiplikative Halbnormen.

Veranschaulichung

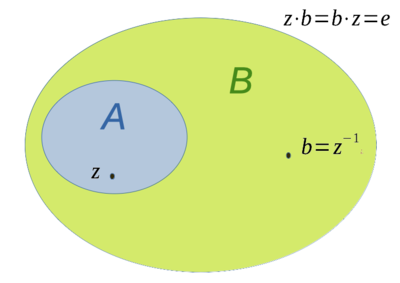
Algebraerweiterung $B$ von $A$ ist hier eine mulitplikative lokalkonvexe Algebra, die ein inverses Element $b=z^{-1}\in B$ zu einem gegebenen $z\in A$ enthält.

Aufgabe

• Negieren Sie die Aussage, dass $z\in A$ kein topologischer Nullteiler ist und formulieren $z\notin {\mathcal {TNT}}(A)$ für ein submultiplikative Halbnormensystem $\|\cdot \|_{\mathcal {A}}$.
• Zeigen Sie, dass in einer ${\mathcal {MLC}}$-Algebra mit $z\in A$ ${\mathcal {MLC}}(A)$-regulär ist, wenn folgende Bedingung gilt (siehe Zelazko 1971)

$\forall _{\alpha \in {\mathcal {A}}}\exists _{\beta \in {\mathcal {A}},\,D_{\beta }>0}\forall _{x\in A}\,\,\|x\|_{\alpha }\leq \|x\|_{\beta }\leq D_{\beta }\cdot \|z\cdot x\|_{\beta }$.

• Zeigen Sie mit der Charakterisierung der ${\mathcal {MPC}}(A)$-Regularität, dass die ${\mathcal {MLC}}(A)$-singulären Elemente genau die topologischen Nullteiler sind.

Multiplikative lokalkonvexe Algebraerweiterung

Sei ${\textstyle {\mathcal {MLC}}_{e}}$ die Klasse der multiplikativen lokalkonvexen unitalen Algebren und ${\textstyle A\in {\mathcal {MLC}}_{e}}$. Die Algebraerweiterung ${\textstyle B\in {\mathcal {MLC}}_{e}}$ bzw. ${\textstyle {\mathcal {MLC}}}$-Erweiterung von ${\textstyle A}$ benötigt nach Definition es einen Algebraisomorphismus ${\textstyle \tau :A\longrightarrow A'\subset B}$ mit:

• ${\textstyle \tau (e_{_{A}})=e_{_{B}}}$, wobei ${\textstyle e_{_{A}}}$ ist das Einselement von ${\textstyle A}$ und ${\textstyle e_{_{B}}\in A'}$ das Einselement von ${\textstyle B}$ ist.
• ${\textstyle A}$ ist homöomorph zu ${\textstyle A'}$; d.h. ${\textstyle \tau }$ und ${\textstyle \tau ^{-1}:A'\longrightarrow A}$ sind stetig.

Algebraisomorphismus in den Quotientenräumen

Der Algebraisomorphismus wird über normierte Quotientenalgebren $A_{\alpha }$ definiert. wobei mit  :$\tau _{\alpha }:A_{\alpha }\to A'_{\alpha }\subset B_{\alpha }$ mit $\tau _{\alpha }(x)=[x]_{\alpha }\in A'_{\alpha }$ bezeichnet und

$\tau :A\longrightarrow A'\subset \prod _{\alpha \in {\mathcal {A}}}A_{\alpha }\subset \prod _{\alpha \in {\mathcal {A}}}B_{\alpha }=B{\mbox{ mit }}\tau (x):=(\tau _{\alpha }(x))_{\alpha \in {\mathcal {A}}}$

Algebraerweiterung von MLC-Quotientenalgebren

Embettung in Quotientenräume bzgl. der submultiplikativen Halbnormen.

Algebraisomorphismus - Einbettung in die Algebraerweiterung

• Im allgemeinen identifiziert man ${\textstyle A}$ mit ${\textstyle A'}$ und schreibt ${\textstyle A\subset B}$. In der jeweiligen Konstruktion der Algebraerweiterung sieht man, dass die Element aus $x\in A$ mit Elementen $\tau (x)=x+I\in B$ in einem Quotientenraum $B:=A[t]/I$ identifiziert werden.
• Sei ${\textstyle {\mathfrak {U}}_{A'}(0)}$ eine Nullumgebungsbasis der Relativtopologie von ${\textstyle B}$ auf ${\textstyle A'}$ und ${\textstyle {\mathfrak {U}}_{A}(0)}$ eine Nullumgebungsbasis von ${\textstyle A}$, dann kann man die Homöomorphie zwischen ${\textstyle A}$ und ${\textstyle A'}$ wie immer über die Topologie ausdrücken:

${\begin{array}{rcl}\forall _{\displaystyle V\in {\mathfrak {U}}_{A}(0)}\exists _{\displaystyle U\in {\mathfrak {U}}_{A'}(0)}&:&U\subset V\,\,\,(\tau (U)\subset V)\\\forall _{\displaystyle U\in {\mathfrak {U}}_{A'}(0)}\exists _{\displaystyle V\in {\mathfrak {U}}_{A}(0)}&:&V\subset U\,\,\,(\tau ^{-1}(V)\subset U).\end{array}}$

Stetigkeit über Halbnormen

Betrachtet man die Halbnormen ${\textstyle \left\|\cdot \right\|_{\widetilde {\mathcal {A}}}}$ und ${\textstyle \left\|\cdot \right\|_{\mathcal {A}}}$ für Nullumgebungen, so lassen sich die oberen beiden Aussagen wie folgt umformulieren (siehe auch Stetigkeitssatz für lineare Abbildungen):

${\begin{array}{rcl}\forall _{\alpha \in {\mathcal {A}}}\exists _{{\widetilde {\alpha }}\in {\widetilde {\mathcal {A}}},C_{1}(\alpha )>0}\forall _{x\in A}&:&\left\|x\right\|_{\alpha }\leq C_{1}(\alpha )\cdot \left\|\tau (x)\right\|_{\widetilde {\alpha }}\\{\mbox{ bzw. }}&&\left\|\cdot \right\|_{A}\leq C_{1}\cdot \left\|\cdot \right\|_{A'}\circ \tau \\\forall _{{\widetilde {\alpha }}\in {\mathcal {A}}}\exists _{\alpha \in {\mathcal {A}},C_{2}({\widetilde {\alpha }})>0}\forall _{x\in A}&:&\left\|\tau (x)\right\|_{\widetilde {\alpha }}\leq C_{2}{\widetilde {\alpha }}\cdot \left\|x\right\|_{\alpha }\\{\mbox{ bzw. }}&&\left\|\cdot \right\|_{A'}\circ \tau \leq C_{2}\cdot \left\|\cdot \right\|_{A}.\end{array}}$

Konstruktion Algebraisomorphismus

Für die Konstruktion des Algebraisomorphismus geht man wie folgt vor:

• (KA1) man konstruiert zunächst einen Algebrahomomorphismus $\tau :A\to B$ und zeigt, dass dieser stetig ist.
• (KA2) man zeigt, dass der Algebrahomomorphismus injektiv ist $Kern(\tau )=\{0_{A}\}$
• (KA3) man definiert mit $A':=\tau (A)\subset B$, die Umkehrabbildung $\tau ^{-1}:A'\to A$ und zeigt, dass $\tau ^{-1}$ ebenfalls stetig ist (siehe Stetigkeitssatz für lineare Abbildungen).

Verwendung der Charakterisierung B-regulärer Elemente

Wir betrachten zunächst multiplikativ lokalkonvexe kommuntative Algebren $(A,\|\cdot \|_{\mathcal {A}})$ und nutzen die Charakterisierung ${\mathcal {B}}$-Regularität für die ${\mathcal {MLC}}$-Erweiterung von $(A,\|\cdot \|_{A})$.

Halbnormensystem unital positiv

Ohne Einschränkung seien die submultiplikativen Halbnormen unital positiv, d.h. $\|e_{A}\|_{\alpha }>0$ für alle $\alpha \in {\mathcal {A}}$. Falls das nicht der Fall ist, geht man zu einem äquivalenten Halbnormensystem über $\|e_{A}\|_{\alpha }^{(+)}>0$ über. Weil $(A,\|\cdot \|_{\mathcal {A}})$ Hausdorffraum ist, gibt es ein $\alpha _{o}\in {\mathcal {A}}$ mit $\|e_{A}\|_{\alpha _{o}}>0$. Man definiert dann $U_{\alpha }=B_{1}^{\alpha }(0_{A})\cap B_{1}^{\alpha _{o}}(0_{A})$ und

$\|x\|_{\alpha }^{(+)}:=p_{U_{\alpha }}(x)=\max\{\|x\|_{\alpha },\|x\|_{\alpha _{o}}\}$

als Minkowski-Funktional von $U_{\alpha }$ und $U_{\alpha }\cdot U_{\alpha }\subset U_{\alpha }$, da $\|\cdot \|_{\alpha }$ und damit auch $\|\cdot \|_{\alpha _{o}}$ submultiplikativ sind. $U_{\alpha }$ ist eine offene Menge in $A$, da $U_{\alpha }$ als Schnitt von zwei offenen Mengen definiert ist und der endliche Schnitt von offenen Mengen in einer Topologie ist wieder offen.

Aufgabe - Äquivalenz des Halbnormensystems - unital positiv

Zeigen Sie, dass die Halbnormensysteme $\|\cdot \|_{\mathcal {A}}$ und $\|\cdot \|_{\mathcal {A}}^{(+)}$ äquivalente Gaugefunktionalsysteme sind!

Aufgabe - TNT-Negation und unital positives Halbnormensystem

Ohne Einschränkung sei das gegebene Halbnormensystem $\|\cdot \|_{\mathcal {A}}$ auf einer unital positiven ${\mathcal {MLC}}$-Algebra $A$. Ferner sei $z\in A$ kein topologischer Nullteiler ($z\notin {\mathcal {TNT}}(A)$). Zeigen Sie, dass für alle $\alpha \in {\mathcal {A}}$ ebenfalls $\|z\|_{\alpha }>0$ gilt.

Topologische Nullteiler in MLC-Algebren

Wenn $z\in {\mathcal {TNT}}(A)$ erfüllt ist, gibt es ein $\alpha \in {\mathcal {A}}$, sodass für alle $\beta \in {\mathcal {A}}$ gilt

$\inf _{x\in A\,\,\|x\|_{\alpha }=1}\|z\cdot x\|_{\beta }=0$

Topologische Nullteiler in Quotientenalgebren

Damit ist insbesondere für $\beta \in {\mathcal {A}}$ mit $\beta \geq \alpha$ (d.h. $\|x\|_{\beta }\geq \|x\|_{\alpha }$ für alle $x\in A$ die folgende Bedingung erfüllt

$\inf _{\|x\|_{\beta }=1}\|z\cdot x\|_{\beta }=0.$

Abschätzung für Eigenschaft in Quotientenalgebren 1

Man erhält die folgenden Abschätzung für $\gamma \geq \alpha$, d.h. ${\frac {1}{\|x\|_{\gamma }}}\leq {\frac {1}{\|x\|_{\alpha }}}$ für alle $\beta \in {\mathcal {A}}$ und alle $x\in A$:

${\begin{array}{rcl}0&=&\displaystyle \inf _{\|x\|_{\alpha }=1}\left\|z\cdot x\right\|_{\beta }=\displaystyle \inf _{\|x\|_{\alpha }>0}\left\|z\cdot {\frac {x}{\|x\|_{\alpha }}}\right\|_{\beta }\\&\geq &\displaystyle \inf _{\|x\|_{\gamma }>0}\left\|z\cdot {\frac {x}{\|x\|_{\alpha }}}\right\|_{\beta }\geq \displaystyle \inf _{\|x\|_{\gamma }>0}\left\|z\cdot {\frac {x}{\|x\|_{\gamma }}}\right\|_{\beta }\\&\geq &\displaystyle \inf _{\|x\|_{\gamma }=1}\left\|z\cdot x\right\|_{\beta }\geq 0\\\end{array}}$

Abschätzung für Eigenschaft in Quotientenalgebren 2

Insgesamt erhält man für $z\in {\mathcal {TNT}}(A)$ die äquivalente Bedingung:

$\exists _{\alpha \in {\mathcal {A}}}\forall _{\beta \in {\mathcal {A}},\,\,\gamma \geq \alpha }\forall _{x\in A}\,\,\displaystyle \inf _{\|x\|_{\gamma }=1}\|z\cdot x\|_{\beta }=0.$

Insbesondere gilt für alle $\beta \geq \alpha$

$\exists _{\alpha \in {\mathcal {A}}}\forall _{\beta \in {\mathcal {A}},\,\,\beta \geq \alpha }\forall _{x\in A}\,\,\displaystyle \inf _{\|x\|_{\beta }=1}\|z\cdot x\|_{\beta }=0$.

TNT-Eigenschaft in Quotientenalgebren

Also gibt es mindestens ein $\alpha \in {\mathcal {A}}$, sodass für alle $\beta \geq \alpha$ gilt:

$z_{\beta }\in {\mathcal {TNT}}(A_{\beta })={\mathcal {TNT}}(A/N_{\beta })$.

MLC-Singularität 1

Wenn man die ${\mathcal {MLC}}$-Singularität betrachtet, gibt es zu jedem $\alpha \in {\mathcal {A}}$ ein $\beta \in {\mathcal {A}}$ mit $\beta \geq \alpha$, sodass $z_{\beta }\notin {\mathcal {TNT}}(A_{\beta })$ und es gilt mit der Eigenschaft $z\notin {\mathcal {TNT}}(A)$ erhält man die Eigenschaft:

$\forall _{\alpha \in {\mathcal {A}}}\exists _{\beta \in {\mathcal {A}},\,D_{\beta }>0,\,\gamma \geq \alpha }\forall _{x\in A}\,\,\|x\|_{\gamma }\leq D_{\beta }\cdot \|z\cdot x\|_{\beta }\,\,\,(\ast )$.

Negation der TNT-Eigenschaft

Mit der Eigenschaft $z\notin {\mathcal {TNT}}(A)$ erhält man zunächst einmal die Abschätzung:

$\forall _{\alpha \in {\mathcal {A}}}\exists _{\beta \in {\mathcal {A}},\,D_{\beta }>0}\forall _{x\in A}\,\,\|x\|_{\alpha }\leq D_{\beta }\cdot \|z\cdot x\|_{\beta }\,\,\,(\ast )$.

Vergleich zur Charakterisierung der MLC-Singularität

Durch die Negation erhält man, dass es zu jedem $\alpha \in {\mathcal {A}}:$ ein $\beta \in {\mathcal {A}}$, in dem $z_{\beta }\in {\mathcal {A_{\beta }}}$ also kein topologischer Nullteiler ist. Diese Negation liefert nach

$\forall _{\alpha \in {\mathcal {A}}}\exists _{\beta _{\alpha }\in {\mathcal {A}},\,D_{\beta _{\alpha }}>0}\forall _{x\in A}\,\,\|x\|_{\alpha }\leq \|x\|_{\beta }\leq D_{\beta }\cdot \|z\cdot x\|_{\beta }\,\,\,(\ast )$.

Aufgabe - Äquivalenz des Halbnormensystems - TNT

Wir definieren darüber nun ein weiteres Halbnormensystem $\|\cdot \|_{\widetilde {\mathcal {A}}}$ aus submultiplikativen Halbnormen wie folgt über die Eigenschaft von $z\in A$, kein topologischer Nullteiler zu sein:

• ${\widetilde {\mathcal {A}}}\subseteq {\mathcal {A}}$
• $\beta _{\alpha }\in {\widetilde {\mathcal {A}}}$, wenn $\alpha \in {\mathcal {A}}$ und $\beta _{\alpha }\in {\mathcal {A}}$ mit $D_{\beta _{\alpha }}>0$ die obige Gleichung $(\ast )$ erfüllt. Zeigen Sie, dass $\|\cdot \|_{\widetilde {\mathcal {A}}}$ und $\|\cdot \|_{\mathcal {A}}$ äquivalente Gaugefunktionalsysteme sind

Notation - Produktraum

Sei $I\not =\emptyset$ eine Indexmenge. In der folgenden Charakterisierung der ${\mathcal {MLC}}$-Regularität werden Produkträume definiert bzw. als Algebraerweiterung konstruiert. Dabei wird folgende Kurzschreibweise des Produktraumes $M$ verwendet.

$M=(M_{i})_{i\in I}:=\prod _{i\in I}M_{i}:=\{(x_{i})_{i\in I}:\,x_{i}\in M_{i}{\text{ für alle }}i\in I\}$

Beweisidee: Konstruktion der MLC-Algebraerweiterung

Ausgehend von $(A,\|\cdot \|_{\mathcal {A}})$ wird ein Produktraum $((A_{\alpha })_{\alpha \in {\mathcal {A}}},\|\!|\cdot |\!\|_{\mathcal {A}})$ von normierten Algebren $(A_{\alpha },\|\!|\cdot |\!\|_{\alpha })$ betrachtet und topologisiert. Auf die normierten Algebren wird mit der Eigenschaft $z\notin {\mathcal {TNT}}(A)$ die gesuchte Eigenschaft $\|\!|[x]_{\alpha }|\!\|_{\alpha }\leq D_{\alpha }\cdot \|\!|[z]_{\alpha }\cdot [x]_{\alpha }|\!\|_{\alpha }$ geliefert und auf alle normierten Algebren $(A_{\alpha },\|\!|\cdot |\!\|_{\alpha })$ angewendet, um eine Algebraerweiterung $(B_{\alpha },\|\!|\cdot |\!\|_{B_{\alpha }})$ zu erhalten, in der $[z]_{\alpha }\in A_{\alpha }$ invertierbar ist.

Algebraisomorphismus in den Quotientenräumen

Der Algebraisomorphismus wird dann mit

$\tau _{\alpha }:A_{\alpha }\to A'_{\alpha }\subset B_{\alpha }$,

mit $\tau _{\alpha }([z]_{\alpha })=z_{\alpha }\in A'_{\alpha }$ bezeichnet.

Algebraerweiterung von MLC-Quotientenalgebren

Embettung in Quotientenräume bzgl. der submultiplikativen Halbnormen.

Schritt 1: Übergang zu Quotientenräumen

Man betrachtet für jede submultitplikative Halbnorm $\|\cdot \|_{\alpha }$ das Ideal

$N_{\alpha }:=\{x\in A\,\colon \,\|x\|_{\alpha }=0\}$

Dann definiert man $A_{\alpha }$ als Quotientenraum $A_{\alpha }:=A/N_{\alpha }$.

Aufgabe: Idealeigenschaften nachweisen

Zeigen Sie, dass $N_{\alpha }$ ein Ideal in $A$ und $A_{\alpha }$ eine Algebra.

Schritt 2: Topologisierung der Quotientenräume

Man verwendet als Halbnorm auf dem Quotientenraum die $\|\!|\cdot |\!\|_{\alpha }$ mit

$\|\!|\,[x]_{\alpha }|\!\|_{\alpha }:=\|\!|\underbrace {x+N_{\alpha }} _{=[x]_{\alpha }}|\!\|_{\alpha }=\displaystyle \inf _{u\in N_{\alpha }}\|x+u\|_{\alpha }$

Aufgaben: Submultiplikative Halbnorm im Quotientenraum

Zeigen Sie, dass $\|\!|\cdot |\!\|_{\alpha }$ eine submultiplikative Norm auf dem Quotientenraum $A_{\alpha }$ ist und $\|\!|\,[x]_{\alpha }|\!\|_{\alpha }=\|x\|_{\alpha }$ gilt.

Schritt 3: Inverse im Quotientenraum

Für die normierten Algebren $(A_{\alpha },\|\!|\cdot |\!\|_{\alpha })$ nutzt man die Charakterisierung der ${\mathcal {B}}$-Regularität und erhält Algebraerweiterungen $(B_{\alpha },\|\!|\cdot |\!\|_{B_{\alpha }})$ in denen $z_{\alpha }\in A_{\alpha }$ das inverse Element $[b_{\alpha }]_{\alpha }\in B_{\alpha }$ mit dem Algebraisomorphismus der Einbettung $\tau _{\alpha }:A_{\alpha }\to A'_{\alpha }\subset B_{\alpha }$ mit einem Inversen Element $b_{\alpha }\in B_{\alpha }$ zu $[z]_{\alpha }\in A_{\alpha }$ d.h.

$z_{\alpha }\cdot b_{\alpha }=b_{\alpha }\cdot z_{\alpha }=e_{\alpha }=t_{\alpha }(\underbrace {e_{A}+N_{\alpha }} _{[e_{A}]_{\alpha }})$

Aufgabe: Positivität der Halbnorm für das inverse Element

Zeigen Sie, dass $\|\!|z_{\alpha }|\!\|_{B_{\alpha }}>0$ und $\|\!|b_{\alpha }|\!\|_{B_{\alpha }}>0$ für alle $\alpha \in {\mathcal {A}}$ erfüllt sind, wenn $z\notin {\mathcal {TNT}}(A)$ ist. Nutzen Sie dazu die Eigenschaft, dass das Halbnormensystem $\|\!|\cdot |\!\|_{\alpha }$ unital positiv ist und mit $\tau _{\alpha }:A_{\alpha }\to A'_{\alpha }$ eine Isometrie vorliegt.

Aufgabe: Unitale Positivität der Halbnormen und inverse Elemente in Quotientenräumen

Zeigen Sie, dass in einem unital positiven multipliklativen Halbnormensystem $(\|\cdot \|_{\mathcal {A}})$ ein Element $z\in A$ genau dann in ${\mathcal {MLC}}$-regulär ist, wenn es ${\mathcal {B}}$-regulär in jeder normierten Algebra $(A_{\alpha },\|\!|\cdot |\!\|_{\alpha })$ für alle $\alpha \in {\mathcal {A}}$ ist mit:

$\|\!|\,[x]_{\alpha }|\!\|_{\alpha }:=\|\!|\underbrace {x+N_{\alpha }} _{=[x]_{\alpha }}|\!\|_{\alpha }=\displaystyle \inf _{u\in N_{\alpha }}\|x+u\|_{\alpha }$

Schritt 4: Definition des Algebraisomorphismus

Der Algebraisomorphismus $\tau :A\to A'\subset B$ setzt sich aus zwei verketteten Abbildungen $\tau :=\tau _{2}\circ \tau _{1}$ zusammen mit ${\widehat {A}}:=\{([x]_{\alpha })_{\alpha \in {\mathcal {A}}}\,:\,x\in A\}$:

• $\tau _{1}:A\to {\widehat {A}}\subset (A_{\alpha })_{\alpha \in {\mathcal {A}}}$ mit $\tau _{1}(x)=([x]_{\alpha })_{\alpha \in {\mathcal {A}}}$
• $\tau _{2}:{\widehat {A}}\to A'\subset (A'_{\alpha })_{\alpha \in {\mathcal {A}}}\subset B=(B_{\alpha })_{\alpha \in {\mathcal {A}}}$ mit $\tau _{2}(x')=\tau _{2}\left(([x]_{\alpha })_{\alpha \in {\mathcal {A}}}\right)=(x_{\alpha })_{\alpha \in {\mathcal {A}}}$

Aufgabe: Surjektivität und Produktraum

Zeigen Sie zunächst, dass $\tau _{1}$ und $\tau _{2}$ Algebraisomorphismen von Algebraerweiterungen sind!

Aufgabe: Surjektivität und Produktraum

Ersetzt man den Wertebereich ${\widehat {A}}:=\{([x]_{\alpha })_{\alpha \in {\mathcal {A}}}\,:\,x\in A\}$ durch den Produktraum der Quotientenräume $(A_{\alpha })_{\alpha \in {\mathcal {A}}}$, so ist die modifizierte Abbildungen ${\widetilde {\tau _{1}}}$ keine Algebraisomorphismen mehr. Begründen Sie, warum ist ${\widetilde {\tau _{1}}}:A\to (A_{\alpha })_{\alpha \in {\mathcal {A}}}$ mit geändertem Wertebereich nicht mehr surjektiv ist, wenn ${\mathcal {A}}$ mehr als einen Index enthält?

Schritt 5: Neutrales Element im Produktraum

Das neutrale im Produktraum erhält man damit über $\tau$ mit:

$\tau (e_{A})=\tau _{2}\left(([e_{A}]_{\alpha })_{\alpha \in {\mathcal {A}}}\right)=\tau _{2}\left((e_{A}+N_{\alpha })_{\alpha \in {\mathcal {A}}}\right)=(e_{\alpha })_{\alpha \in {\mathcal {A}}}=:e_{B}$.

Die Invertierbarkeit im Produktraum $B=(B_{\alpha })_{\alpha \in {\mathcal {A}}}$ erhält man über

${\begin{array}{rcl}e_{B}&=&\tau (e_{A})=(e_{\alpha })_{\alpha \in {\mathcal {A}}}=(z_{\alpha }\cdot b_{\alpha })_{\alpha \in {\mathcal {A}}}\\&=&(z_{\alpha })_{\alpha \in {\mathcal {A}}}\cdot (b_{\alpha })_{\alpha \in {\mathcal {A}}}=\tau (z)\cdot b\end{array}}$.

Bermerkung: Notation der Elemente in der Algebraerweiterung

Man muss bei der Notation in der Algebraerweiterung folgenden Notationen unterscheiden:

• $(b_{\alpha })_{\alpha \in {\mathcal {A}}}\in (B_{\alpha })_{\alpha \in {\mathcal {A}}}$
• $([z]_{\alpha })_{\alpha \in {\mathcal {A}}}=(z+N_{\alpha })_{\alpha \in {\mathcal {A}}}\in (A_{\alpha })_{\alpha \in {\mathcal {A}}}$ mit $z\in A$

In der zweiten Schreibweise gibt es in jeder Komponente $\alpha \in {\mathcal {A}}$ des Produktraumes $(A_{\alpha })_{\alpha \in {\mathcal {A}}}$ den gleichen Repräsentanten $z\in A$, während in der ersten Schreibweise für die Notation des Inversen die Repräsentanten $b_{\alpha }$ für jedes $\alpha \in {\mathcal {A}}$ unterschiedlich sein können.

Isometrische Abbildung

Nach Konstruktion der Algebraerweiterung der normierten Algebra $(A_{\alpha },\|\!|\cdot |\!\|_{\alpha })$ Algebraerweiterungen auf $(B_{\alpha },\|\!|\cdot |\!\|_{B_{\alpha }})$ nach der Charakterisierung der ${\mathcal {B}}$-Regularität ist die Algebraerweiterung eine Isometrie, d.h. für alle $x\in A$ gilt für alle $\alpha _{0}\in {\mathcal {A}}$:

$\|\!|\,([x_{\alpha }]_{\alpha })_{\alpha _{0}\in {\mathcal {A}}}\,|\!\|_{\alpha }=\|\!|\tau _{2}\left(\,([x_{\alpha }]_{\alpha })_{\alpha \in {\mathcal {A}}}\,\right)|\!\|_{B_{\alpha _{0}}}$

Schritt 6: Topologisierung der Algebraerweiterung

Für alle $\alpha _{o}\in {\mathcal {A}}$ definiert man mit $\tau (x)=([x]_{\alpha })_{\alpha \in {\mathcal {A}}}\in (B_{\alpha })_{\alpha \in {\mathcal {A}}}$ und für ${\widehat {b\,}}:=([{\widehat {b\,}}_{\alpha }]_{\alpha \in {\widetilde {A}}}\in B$ setzt man

$\|{\widehat {b\,}}\|_{\alpha _{o}}:=\|\,([{\widehat {b\,}}_{\alpha }])_{\alpha \in {\mathcal {A}}}\|_{\alpha _{o}}:=\|\!|\,[{\widehat {b\,}}_{\alpha _{o}}]_{\alpha _{o}}|\!\|_{\alpha _{o}}$.

Aufgabe: Zeigen Sie, dass der Algebraisomorphismus $\tau$ eine Isometrie ist, d.h.

$\forall _{\alpha _{o}\in {\mathcal {A}}}\forall _{x\in A}\,\,\|x\|_{\alpha _{o}}=\|\!|\tau (x)|\!\|_{\alpha _{o}}$

Schritt 7: Inverses Element in der Algebraerweiterung

Das inverse Element von $z$ ist dann in $B:=(B_{\alpha })_{\alpha \in {\mathcal {A}}}$ mit einem inversen Element $b\in B$, das komponentenweise als $b:=(b_{\alpha })_{\alpha \in {\mathcal {A}}}\in B$ definiert wird mit $b_{\alpha }\in B_{\alpha }$ für alle $\alpha \in A$.

Bemerkung: Vollständigkeit

Die Vollständigkeit, die für die B-Regularität noch betrachtet wurde, spielt hier für die ${\mathcal {MLC}}$-Regularität keine Rolle, da nur das Vorgehen für Konstruktion einer Algebraerweiterung zu einer normierten Algebra $((A_{\alpha })_{\alpha \in {\mathcal {A}}},\|\!|\cdot |\!\|_{\mathcal {A}})$ benötigt wird.

Geschichte

Der Beweis der Charakterisierung ${\mathcal {MLC}}$-Regularität wurde von Zelazko bereits 1971 gezeigt als Charakterisierung der permant singulären Elemente von ${\mathcal {MLC}}$-Algebren.

Spezialfall der MPC-Regularität

Der Nachweis der Charakterisierung der ${\mathcal {MLC}}$-Regularität ist ein Spezialfall der ${\mathcal {MPC}}$-Regularität für multplikative pseudokonvexe Räume, wobei die $p$-Normen mit $p=1$ homogen sind und damit die Eigenschaften einer Norm erfüllt.

Algebraisomorphismen

Bei der ${\mathcal {MLC}}$-Regularität wurde die Algebraerweiterung $B$ über die ${\mathcal {B}}$-Regularität, die Definition von isometrischen Algebraisomorphismen und der Betrachtung von Quotientenräume konstruktiert, in der ein $z\notin {\mathcal {TNT}}(A)$ invertierbar ist.

Direkte Konstruktion der Algebraerweiterung

Eine direkte Konstruktion der Algebraerweiterung über die topologische Eigenschaften von $z\in A$ ist für ${\mathcal {MLC}}$-Regularität ebenfalls möglich. Dabei wird wieder die Polynomalgebra $A[t]$ topologisiert und dann der Quotientenraum $A[t]/I$ betrachtet, wobei dann $I$ das Hauptideal $I:=o\cdot A[t]$ ist und $o(t):=z\cdot t-e_{A}$ ein Repräsentant des Nullvektors $0_{B}$ in der Algebraerweiterung $B=A[t]/I$ ist. Der direkte Beweis wird bei der Charakterisierung der ${\mathcal {MPC}}$-Regularität geführt und kann mit $p=1$ auf ${\mathcal {MLC}}$-Regularität übertragen werden.

Siehe auch

• Algebraerweiterung
• Konstruktion des Algebraisomorphismus
• Halbnorm
• Gaugefunktional
• Äquivalenz (Gaugefunktionalsysteme)
• Ideal (Algebra)
• Normen, Metriken, Topologie
• Minkowski-Funktional
• P-Regularität
• P-Regularität über Quasinormen
• B-Regularität
• LC-Regularität
• MPC-Regularität
• Topologisierungslemma für Algebren
• topologische Nullteiler
• Relativtopologie

Seiteninformation

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Topologische Invertierbarkeitskriterien' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

• Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
• Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Topologische%20Invertierbarkeitskriterien/MLC-Regularit%C3%A4t
• siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.