Kurs:Mathematische Modellbildung/Themen/Sport - Elfmeterschießen
Modellierungsproblem
[Bearbeiten]Definition
[Bearbeiten]
,,Auf Strafstoß ist zu entscheiden, wenn die verteidigende Mannschaft in ihrem Strafraum eine Regelübertretung begeht, die im restlichen Spielfeld mit einem direkten Freistoß zu ahnden wäre (meist ein Foul oder ein Handspiel). [...] Der Strafstoß wird von einem Punkt fast genau 11 Meter (oder in der englischsprachigen Norm auch 12 yards = 10,9728 m) von der Torlinie in Richtung Mittelpunkt durchgeführt. Im Gegensatz zum Freistoß, bei dem nur die Verteidiger den Abstand einzuhalten haben, müssen beim Strafstoß alle Spieler außer dem Schützen der angreifenden Mannschaft und dem Torwart der verteidigenden Mannschaft mindestens 9,15 m oder 10 yards (9,144 m) vom Ball entfernt [sein] (vgl. [1])
Einführung
[Bearbeiten]Wenn ein Schiedsrichter pfeift und auf den Elfmeterpunkt zeigt, ist die Freude der Mannschaft, die den Elfmeter zugesprochen bekommt, groß, so ist es doch für viele schon ein sicheres Tor. Dennoch gibt es Situationen, in denen die Verteidiger einen Angreifer im Sechzehnmeterraum foulen oder mit Absicht die Hand benutzen, um ein Tor zu verhindern. Die Folge ist dann ein Elfmeter und oft auch ein Platzverweis. Sie sehen den Elfmeter als Chance, doch kein Tor zu kassieren. Luis Suarez ist ein Paradebeispiel. Bei der WM 2010 rettete er den Ball auf der Linie mit der Hand und hat somit ein Gegentor verhindert, allerdings eine rote Karte bekommen und es wurde auf Elfmeter entschieden. Die Freude im uruguayischen Team war groß als Ghana den Elfmeter verschießt, sich Uruguay so ins Elfmeterschießen rettet, und am Ende sogar ins Halbfinale einzieht. Es stellt sich nun die Frage, ob Elfmeter wirklich als sicheres Tor gelten können oder die Wahrscheinlichkeit des Verschießens doch höher ist als man eigentlich annimmt.
Ziel der Modellierung
[Bearbeiten]Das Ziel der Modellbildung ist es zunächst, die Trefferwahrscheinlichkeit bei einem Elfmeter in Abhängigkeit der vom Schützen gewählten Ecke oder „Zone“ zu bestimmen. Aufgrund dieser Analyse soll das Üben des Elfmeterschießens angepasst und das Verhalten beim Elfmeterschießen optimiert werden. Dies soll neben dem Schützen auch den Torhütern oder Trainern helfen. Im weiteren Verlauf wird dann auch deutlich ob Aktionen, wie Luis Suarez sie durchgeführt hat, sinnvoll sein können. Im weiteren Verlauf soll dann die Schussgeschwindigkeit betrachtet werden. Wie fest muss man schießen, damit der Ball für den Torwart an einem bestimmten Treffpunkt unhaltbar wird? Dafür sollen verschiedene Faktoren, die innerhalb des Elfmeterschießens eine Rolle spielen, berücksichtigt werden.
- Sek I: Geometrische Einteilung des Tores in mehrere Rechtecke, relative und absolute Häufigkeit, Histogramm, Flächenansatz
- Sek II:
- Berechnung des Erwartungswertes, der Varianz und der Standardabweichung der Treffer- und Paradenwahrscheinlichkeit
- Berechnung der zu überschreitenden Geschwindigkeit des Ball für ein sicheres Tor unter Betrachtung des Treffpunktes und des Torwarts
- Uni: Weiterführung des Geschwindigkeit-Modells unter Betrachtung weiterer entscheidender Faktoren (z.B. Winkelgeschwindigkeit des Arms)
Zielgruppe der Modellbildung
[Bearbeiten]Zur Zielgruppe der Modellbildung gehören vor allem Trainer/innen und Spieler/innen, die einen Elfmeter schießen. Dabei sollen sie zunächst eine vereinfachte Wahrscheinlichkeitsverteilung bezüglich neun Feldern, in die das Tor eingeteilt wurde, erhalten. Im weiteren Verlauf solle für sie ein Abwägen zwischen Geschwindigkeit und Präzision möglich sein, indem die zu überschreitende Geschwindigkeit für einen sicheren Treffer modelliert wird. Trainer/innen können diese Erkenntnisse für ihre Planung nutzen und den Spieler/innen Tipps und Tricks mitgeben, die ihnen beim Üben des Elfmeterschießens und in einer Elfmetersituation innerhalb eines Wettkampfes weiterhelfen können.
Mehrwert der Modellbildung
[Bearbeiten]Im schulischen Kontext sind vor allem in der Sekundarstufe 1 viele Schülerinnen und Schüler sportlich motiviert. Durch eine Modellbildung im sportlichen Bereich kann zunächst durch die eigenständige Datenerhebung ein fächerübergreifendes Lernen ermöglicht werden, wobei neben der Motivation für den Sport, in diesem Fall für das Fußballspielen, auch die Motivation zur Hinterfragung fußballerischer Entscheidungsprozesse im mathematischen Kontext ermöglicht wird. Durch die weit verbreitete Sportart ist es möglich, die Schülerinnen und Schüler, aber auch außerschulische Personen an die mathematische Modellbildung heranzuführen. Durch die Vorstellung der Erkenntnisse ist außerdem eine Sensibilisierung der Gesellschaft gegenüber der Elfmetersituation möglich, in der sich vor allem die Schießenden unter erhöhtem Erfolgsdruck beweisen müssen. Bei der EM 2020, die im Sommer 2021 stattfand, sind drei englische Nationalspieler, Jadon Sancho, Marcus Rashford und Bukayo Saka, nach ihren Fehlschüssen im Finale gegen Italien von englischen Anhängern rassistisch beleidigt worden. Ein früheres Ereignis schildert die Elfmetersituation zusätzlich: beim "Finale dahoam" 2012 verlor der FC Bayern München das Champions-League-Finale gegen den FC Chelsea im Elfmeterschießen, nachdem Bastian Schweinsteiger den entscheidenden Elfmeter verschoss. Besonders war hier, dass Torhüter Manuel Neuer zum Elfmeter antreten musste, da sich nicht mehr Feldspieler fanden, die zum Schießen bereit waren. Oft ist es die Angst vor dem Versagen, die die Schützen und Schützinnen daran hindert anzutreten. Deshalb kann diese Modellbildung auch zur Sensibilisierung der Gesellschaft dieser Situationen dienen, indem die vereinfachte Wahrscheinlichkeit für einen Treffer und die nötigen Schussgeschwindigkeiten bei hochklassigen Torhütern und Torhüterinnen dargestellt werden. Das Ziel dieser Sensibilisierung sollte dann sein, dass die Aussage, ein Elfmeter sei für den Schützen ein geschenktes Tor, aus den Köpfen der Fußballfans gestrichen wird und Beleidigungen wie kürzlich bei der EM verhindert werden können.
Gruppenmitglieder
[Bearbeiten]- Lena Kasprzyk
- Lukas Rohn
- Robin Schmidt
- Pascal Jäger
Wiki2Reveal
[Bearbeiten]- Einführung
- Mathematische Grundlagen - Zyklus 1
- Mathematische Grundlagen - Zyklus 2
- Mathematische Grundlagen - Zyklus 3
- Modellierungszyklus 1
- Modellierungszyklus 2
- Modellierungszyklus 3
- Bewertung der Modellbildung
- Geogebra
- Excel
- Maxima
Zuordnung zu Nachhaltigkeitszielen
[Bearbeiten]- Die positiven Auswirkungen von Sport auf die körperliche Fitness und Gesundheit ist schon mehrfach wissenschaftlich bewiesen. Die ins unserem Modell fokussierte Sportart Fußball deckt all diese Komponenten ab.
- Hier sieht man in den vergangenen Jahren eine starke positive Veränderung. Während Frauen erst um die 1970er Jahre das Fußballspielen durch den DFB offiziell erlaubt wurde, genießt der Frauenfußball heute immer mehr Anerkennung. Gerade im Kinder-/Jugendfußball findet man immer mehr gemischte Mannschaften.
- Auf dem Platz gelten für allle Spieler die selben Regeln und keiner wird im Vergleich benachteiligt. Des Weiteren sind zahlreiche Inklusionsprogramme im Fußball zu finden, sei es im Profibereich oder im Breitensport.
Modellierungszyklen
[Bearbeiten]Modellierungszyklus 1 - Niveau Sekundarstufe 1
[Bearbeiten]- Aufteilen des Tores in neun Teile (oben, mittig, unten x links, mittig, rechts)
- Aufstellen von relativen und absoluten Häufigkeiten für die Torbereiche
Einfache Theorie des Elfmeters
[Bearbeiten]Nehmen wir an der Schütze trifft immer das Tor und wir haben das Tor in drei gleich große Teile aufgeteilt: Links, Mitte, Rechts. Nehmen wir zunächst weiterhin an, dass ein Elfmeter nur als getroffen gilt, wenn sich der Schütze für einen Teil des Tores entscheidet, den der Torwart nicht ebenfalls ausgewählt hat. Der Torwart hat also eine geringe Chance den Elfmeter zu halten, diese liegt bei ⅓ sprich 33,3%. Der Schütze trifft also immer dann, wenn er eine der zwei Bereiche auswählt, die der Torwart nicht ausgewählt hat. Somit erzielt der Schütze mit einer Wahrscheinlichkeit von ⅔ einen Treffer, sprich 66,6%.
Nun möchten wir aber das Tor nicht nur in drei Teile (Links, Mitte, Rechts) unterteilen, sondern in neun, um möglichst genaue und auch variantenreiche Trefferquoten ermitteln zu können. Das Tor ist somit in unterteilt in links unten(LU), linksmitte(LM), linksoben(LO), mitte unten(MU), mitte mitte (MM), mitte oben (MO), rechts unten (RU), rechts mitte (RM), rechts oben (RO). Ein Elfmeter gilt also als verwandelt, wenn der Torwart nicht nur die selbe Ecke auswählt, sondern auch das selbe Teilfeld. Somit verändern sich auch die Trefferwahrscheinlichkeiten, da der Torwart jetzt nicht mehr 1/3 abdeckt, sondern nur noch 1/9 der Torfläche. Die Trefferwahrscheinlichkeit erhöht sich für die Schützen auf 8/9, sprich etwa 88,89%.
Flächenansatz für den Torwart
[Bearbeiten]Das Tor hat nach der offiziellen Norm des DFB eine Breite von von 7,32m und eine Höhe von 2,44m. Somit ergibt sich für die Torfläche, die getroffen werden kann, folgende Rechnung;
Nun stellt sich die Frage, welche Fläche ein Torwart mit seinen beweglichen Armen und Beinen abdecken kann. Angenommen die durchschnittliche Größe für einen Torwart beträgt ca. 1,88m (vgl. [2]), somit beträgt auch die Armspannweite ungefähr 1,88m, da die Armspannweite ziemlich genau der Körpergröße entspricht (vgl. [3]). Die Schulterhöhe beträgt bei Männern ungefähr 30 cm weniger der Körpergröße, bei unserem Modell hier also ca. 1,58m. ( vgl. [4]) Die Fläche die der Torwart im Stehen abdecken kann, ist ein Rechteck der Schulterhöhe x Armspannweite, addiert um einen Halbkreis, der die Fläche oberhalb der Schultern abdeckt, mit dem Radius 0,94m, der die Arme repräsentiert. Somit ergibt sich folgende Rechnung:
Der Prozentsatz, der also von einem Torwart abgedeckt werden kann liegt bei
, also etwa
Die erhobenen Daten werden später mit der Theorie verglichen und ausgewertet.
Datenerhebung & Ergebnisse
[Bearbeiten]Die im Folgenden betrachteten Daten wurden selbst ausgeführt, gesammelt und ausgewertet.
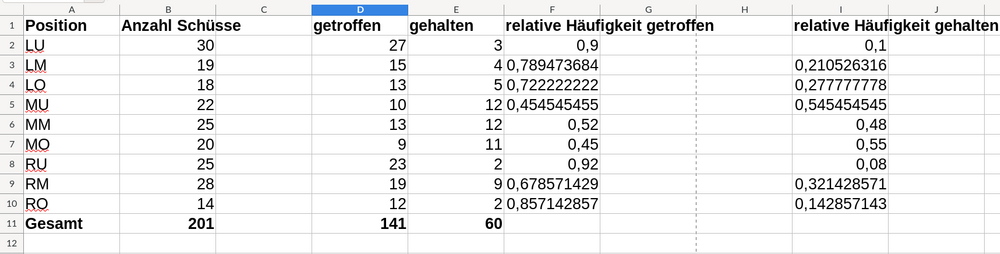
In der Sekundarstufe 1 wird zunächst ein Histogramm über die absoluten Häufigkeiten erstellt. Es werden hier erst einmal nur die Anzahl aller Schüsse, sowie die der getroffenen und gehaltenen Elfmeter berücksichtigt. Insgesamt wurden 201 Elfmeter geschossen.
Es ist zu sehen, dass die absolute Häufigkeit je nach angeschossenem Torfeld variiert. Somit werden mehr Schüsse in den Ecken getroffen und in den mittleren Torfeldern gehalten. Das führt zu folgenden relativen Häufigkeiten
Auswertung
[Bearbeiten]Es ist zu erkennen, dass die Trefferhäufigkeit vor allem in den Eckenzonen sehr hoch ist, während in den mittleren Zonen geringere Trefferhäufigkeiten zu beobachten sind. Besonders häufig wurde in den Zonen Rechts-Unten und Links-Unten getroffen. Hier liegt die Wahrscheinlichkeit für einen Treffer bei 90% oder höher. Insgesamt liegt die Wahrscheinlichkeit eines Treffers bei den erhobenen Daten bei 70,14925373 % . Dem entsprechend ist die Wahrscheinlichkeit höher, dass der Torwart Bälle hält, die in die mittlere Bereiche geschossen werden. Gründe dafür können sein, dass der Torwart einen längeren Weg hat, um einen in der Ecke zu halten und er dabei auch die richtige Ecke wählen muss. Hat er die richtige Ecke gewählt, ist es dennoch möglich, dass ein fester und/oder ein sehr präziser Schuss nicht gehalten werden kann. Bleibt der Torwart aber in der Mitte stehen und der Ball wird vom Schützen auch in die Mitte geschossen, so ist ein Halten des Balles wahrscheinlicher als bei gleicher Situation in einer Ecke, da der Torwart kürzere Wege zurücklegen muss, um den Ball zu halten und alle 3 mittigen Felder abdecken kann. Ebenfalls ist zu beobachten, dass die Felder Rechts-Oben und Links-Oben weniger oft getroffen wurden. Wenn der Schütze diese Zonen aber getroffen hat, liegt auch hier die Trefferwahrscheinlichkeit über dem Durchschnitt.
Des weiteren ist aufgefallen, dass ein Torwart nicht nur ein Torfeld abdeckt, da bei einem mittigen Schuss alle 3 Felder abgedeckt werden, sofern der Torwart auch in der Mitte stehen bleibt. Zudem werden teilweise auch Schüsse nach rechts/links unten gehalten, wenn der Torwart eigentlich rechts/links Mitte springen wollte und umgekehrt. Somit deckt der Torwart in der Mitte 3/9 der Felder, was 33,3% entspricht und in den Ecken 2/9, was 22,2% entspricht, ab. Der Schütze trifft in den Ecken also zu etwa 77,8% und in der Mitte zu 66,67%, was zu einem Mittelwert von 72,2% führt. Da bei dieser Theorie Schüsse an den Pfosten und am Tor vorbei nicht berücksichtigt werden, deckt sich die Theorie sehr mit der relativen Häufigkeit unserer selbst erhobenen Daten von 70,14925373%.
Software
[Bearbeiten]Im ersten Zyklus haben wir das Tabellenkalkulationsprogramm Microsoft Exel verwendet. Zunächst haben wir eine eine Tabelle erstellt, die die Anzahl der Schüsse und die neun verschiedenen Torfelder anzeigt. In diese wurde bei der Datenerhebung eingetragen welches Eck anvisiert wurde, ob der Schuss ein Treffer war oder ob der Torwart den Ball gehalten hat. Anschließend haben wir eine neue Tabelle erstellt, in der die Anzahl der Schüsse und Treffer pro Torfeld eingetragen wurden. Somit entstand eine Tabelle der absoluten Häufigkeiten. Durch diese Daten war es dann auch möglich, die relativen Häufigkeiten auszurechnen, indem man in die Zelle der relativen Häufigkeit die Formel (=Anzahl getroffen/Anzahl Schüsse) eingibt. Durch das Ziehen der Maus wurden dann analog die Werte für die die restlichen Torfelder bestimmt.
Um die Daten in einem Diagramm darzustellen, müssen die Daten ausgewählt und das Feld ,,Diagramm einfügen´´ ausgewählt werden.
Modellierungszyklus 2 - Niveau Sekundarstufe 2
[Bearbeiten]- Berechnung von Erwartungswert, Varianz und Standardabweichung für verschiedene Bereiche des Tors
- Bestimmung der zu überschreitenden Schussgeschwindigkeiten für ein sicheres Tor für einen beliebigen Treffpunkt des Balles im Tor
Erwartungswert, Varianz und Standardabweichung
[Bearbeiten]Nachdem wir im ersten Zyklus die absoluten und relativen Häufigkeiten ermittelt haben, beschäftigen wir uns nun mit Erwartungswert, Varianz und Standardabweichung. Dies sind weitere stochastische Kennzahlen und unsere Daten werden dadurch aussagekräftiger und können besser verglichen werden. Zunächst ermitteln wir Erwartungswert, Varianz und Standardabweichung für die vorher festgelegten neun Torfelder. Da es sich bei uns um ein Zufallsexperiment mit binomialverteilter Zufallsvariable handelt, ist der Erwartungswert für die Anzahl der Tore gleich der Trefferanzahl. Für die Varianz multiplizieren wir den Erwartungswert mit (1-Trefferwahrscheinlichkeit). Abschließend muss für die Standardabweichung noch die Wurzel der Varianz bestimmt werden.
Anschließend teilen wir das Tor vertikal in die Bereiche Links, Mitte und Rechts und horizontal in die Bereiche Unten, Mitte und Oben auf. Hier berechnen wir nochmal Erwartungswert, Varianz und Standardabweichung. So können noch mehr Vergleiche angestellt und Aussagen über anzustrebende Bereiche beim Elfmeter getroffen werden.
Grafische Darstellung der Binomialverteilung
[Bearbeiten]Für die Darstellung der Binomailverteilung greifen wir auf unsere gesamten Daten zurück und betrachten die Wahrscheinlichkeit für einen Treffer unabhängig von der Torfläche. Somit haben wir eine Versuchszahl von 201 Schüssen und eine Wahrscheinlichkeit von 0,701. Mit diesen Werten ergibt sich folgende Binomialverteilung:

Um hier die σ-Regeln der Normalverteilung anwenden zu können, approxximieren wir diese Binomialverteilung durch eine Normalverteilung. Die Approximation sieht grafisch folgendermaßen aus:

Auswertung
[Bearbeiten]Wahrscheinlichkeiten bei vertikaler und horizontaler Aufteilung
[Bearbeiten]Zunächst können durch die Aufteilung in drei vertikale beziehungsweise horizontale Bereiche neue Erkenntnisse hinsichtlich anzuvisierender Bereiche getroffen werden. So sieht man, dass die Wahrscheinlichkeit ein Tor zu erzielen bei der vertikalen Aufteilung links (82,1%) und rechts (80,6%) mit über 80 % hoch ist. Dem gegenüber steht in der Mitte lediglich eine Wahrscheinlichkeit von 47,8 %. Daher spricht vieles dafür eher eine Seite anstatt der Mitte anzuvisieren. Bei der horizontalen Aufteilung liegen ebenfalls deutliche Unterschiede vor. So betragen die Wahrscheinlichkeiten bei Schüssen in den mittleren (65,3 %) und oberen (65,4 %) Bereich jeweils 65 %. Anders sieht es bei flachen Schüssen in den unteren Bereich aus. Hier liegt die Wahrscheinlichkeit bei 77,9 %.
σ-Regeln der Normalverteilung
[Bearbeiten]Durch die Approximierung der Binomialverteilung durch die Normalverteilung lassen sich die σ-Regeln anwenden. Dafür betrachten wir Erwartungswert μ, Standardabweichung σ und die Wahrscheinlichkeit p für einen Treffer.
μ = 140,901
σ = 6,488
p = 0,701
Damit lassen sich nun verschiedenen σ-Intervalle bestimmen. So geht das 1σ-Intervall von μ ± (1 • σ), das 2σ-Intervall von μ ± (2 • σ) und das 3σ-Intervall von μ ± (3 • σ). Für unsere erhobenen Daten sieht dies wie folgt aus:
- 1σ-Intervall = 140,901 ± 1 • 6,488 = [134,41 ; 147,39]
Das bedeutet bei unserer Wahrscheinlichkeit für einen Treffer von 0,701: P (|Z-140,901| ≤ 1•6,488) ≈ 0.6827
- 2σ-Intervall = 140,901 ± 2 • 6,488 = [127,93 ; 153,88]
Das bedeutet bei unserer Wahrscheinlichkeit für einen Treffer von 0,701: P (|Z-140,901| ≤ 2•6,488) ≈ 0.9545
- 3σ-Intervall = 140,901 ± 3 • 6,488 = [121,44 ; 160,37]
Das bedeutet bei unserer Wahrscheinlichkeit für einen Treffer von 0,701: P (|Z-140,901| ≤ 3•6,488) ≈ 0.9973
In Worten lässt sich daher sagen, dass bei einer Trefferwahrscheinlichkeit von 0,701 und einer Versuchszahl von 201 Schüssen die Trefferanzahl zu 68,27 % zwischen 134,41 und 147,39 liegt. Da für die Praxis eher natürliche Zahlen relevant sind, kann man die Trefferanzahl hier auch mit dem Bereich von 135 bis 147 angeben. Analog lässt sich diese Aussage mit den anderen Intervallen treffen.
Weiterführung des Modells
[Bearbeiten]Bisher wurde im ersten und zweiten Modellierungszyklus lediglich vorausgesetzt, dass sich der Torwart und der Schütze jeweils eines der neun festgelegten Felder aussuchen und der Schütze trifft, falls der Torwart sich nicht für das gleiche Feld entscheidet. Nun spielen beim Elfmeterschießen auch weitere Faktoren eine Rolle. Beispielsweise ist von Bedeutung, mit welcher Geschwindigkeit der Ball auf das Tor trifft und auch, wie groß der Torwart ist. Im folgenden sollen nun solche Faktoren eingebaut werden, um das Modell zu verfeinern.
Berechnung der notwendigen Geschwindigkeit des Balles für einen sicheren Treffer
[Bearbeiten]Im folgenden Abschnitt soll der Faktor der Schussgeschwindigkeit beachtet werden. Je nach Trefferposition des Balles im Tor ist eine unterschiedliche Schussgeschwindigkeit notwendig, sodass der Schuss als unhaltbar gewertet werden kann. Die Vermutung ist dabei, dass die nötige Geschwindigkeit umso geringer ist, je größer die Entfernung der Trefferposition zum Torwart ist. Dies soll nun im Allgemeinen modelliert werden.
Um schrittweise die nötige Geschwindigkeit für einen sicheren Treffer herleiten zu können, ist zunächst der Abstand des Elfmeterpunkts, auf dem der Ball zunächst liegt, bis zum Treffpunkt im Tor zu berechnen. Dazu sollen zuerst die Abstände zu den jeweiligen Mittelpunkten der zuvor betrachteten neun Felder berechnet werden.
1. Treffer in die Mitte der neun Felder
Betrachtet man ein Fußballtor im , wobei das linke untere Eck des Tors im Koordinatenursprung liegt, kann man mittels dreidimensionalen Koordinaten die neun Treffpunkte und die Position des Elfmeterpunkts S ausmachen:

Die jeweiligen Entfernungen der Trefferpunkte zum Elfmeterpunkt S zu bestimmen, können dreidimensionale Vektoren genutzt werden. Somit ergeben sich für die neun Punkte folgende Entfernungen zu S. Die eingesetzten Werte sollen beispielhaft für vier Punkte dargestellt werden:

2. Allgemeine Formel zur Berechnung der Entfernung des Treffpunkts zum Elfmeterpunkt
Diese neun Treffpunkte können als Beispiel für die allgemeine Formel aufgefasst werden, die die Entfernung des Elfmeterpunkts zu einem beliebigen Treffpunkt im Tor beschreibt:
3. Zeit bis zum Treffer
Mit dieser Formel ist es nun möglich, die Zeit zu berechnen, die verstreicht, die der Ball nach einem Abschluss bis zum Tor benötigt. Zunächst soll davon ausgegangen werden, dass sich der Ball mit einer Geschwindigkeit von 90 km/h = 25 m/s auf das Tor bewegt. Mit der physikalischen Formel kann nun die benötigte Zeit bis zum Treffer berechnet werden. Mittels WXMaxima kann die Formel so eingefügt werden, dass nur die Werte des Treffpunktes eingegeben werden müssen, um die verstrichene Zeit bis zum Treffer zu berechnen.
4. Entfernung des Torwarts zum Treffpunkt
Um die benötigte Geschwindigkeit für einen sicheren Treffer für einen beliebigen Treffpunkt bestimmen zu können, ist es ebenfalls nötig, den Torwart zu berücksichtigen. Dabei muss betrachtet werden, wie schnell der Torwart zum jeweiligen Treffpunkt gelangt. Die Geschwindigkeit muss am Ende dann so gewählt werden, dass die Zeit des Balles bis zum Treffpunkt geringer ist als die Zeit, die der Torwart bis zum Treffpunkt benötigt. Zunächst muss also wie zuvor beim Ball die Entfernung des Torwarts zu einem beliebigen Treffpunkt im Tor berechnet werden. Zur Vereinfachung des Problems soll betrachtet werden, dass der Torwart den Ball mit den Händen hält, die er vor dem Schuss jeweils neben dem Körper hält. Damit kann die minimale Entfernung des Torwarts bis zum Treffpunkt bestimmt werden. Dabei soll zu Beginn festgelegt werden, dass der Torwart die Hände neben seinem Körper auf 100cm Höhe hält und der Torwart in der Mitte des Tores steht. Dann ergeben sich folgende Handpunkte:


Mithilfe der zwei Handpunkte kann die Entfernung des Torwarts zu einem beliebigen Treffpunkt berechnet werden. Dabei ist zu beachten, dass jeweils die kürzere Entfernung des Treffpunkts zu einem der beiden Handpunkte zu betrachten ist. Daraus ergibt sich folgende Formel für den Abstand von Torwart und Treffpunkt:
5. Zeit des Torwarts bis zum Treffpunkt
Mithilfe des Abstands des Torwarts zum Treffpunkt und seiner Bewegungsgeschwindigkeit kann nun in diesem Modell jedem Punkt , in dem das Tor getroffen wird, eine Geschwindigkeit zugeordnet werden, die angibt, mit welcher Geschwindigkeit der Ball auf das Tor fliegen muss, um sicher im Tor zu landen. Zunächst muss die Zeit berechnet werden, die der Torwart zu einem beliebigen Punkt im Tor benötigt. Dazu soll festgelegt werden, dass sich ein Torwart mit einer Geschwindigkeit von 4m/s fortbewegt. Diese Angabe variiert selbstverständlich von Torwart zu Torwart und wird hier nur zur Vereinfachung festgelegt. Daraus ergibt sich folgende Formel:
Diese Formel ergibt sich aus der Gleichung . Hierbei wird vorausgesetzt, dass der Torwart die Richtung des Balles nicht antizipiert, also nicht schon vor der Schussausführung losspringt, sondern reagiert. Allerdings ist in diesem Modellzyklus die Reaktionszeit des Torwarts zunächst gleich Null gesetzt. Möchte man dies nun allgemein auffassen, ergibt sich folgendes, wenn die Fortbewegungsgeschwindigkeit desTorwarts ist:
6. Geschwindigkeit, die der Ball für einen sicheren Treffer überschreiten muss
Diese Zeit kann nun mit der Zeit des Balles bis zum Treffpunkt verglichen werden, sodass eine Geschwindigkeit für den Ball bestimmt werden kann, sodass der Ball vor dem Torwart den Treffpunkt erreicht. Das heißt, es muss gelten: < . Daraus ergibt sich nun folgende Ungleichung, die nach der Geschwindigkeit des Balles umgestellt werden kann:
<
Mit dieser Ungleichung kann nun die Geschwindigkeit berechnet werden, die der Ball überschreiten muss, um schneller am Treffpunkt im Tor anzugelangen als der Torwart. Dies ist abhängig vom Treffpunkt und der Bewegungsgeschwindigkeit des Torwarts . Dabei ist zu beachten, dass die Bewegungsgeschwindigkeit vorab gegeben sein sollte. Betrachtet man nun noch die Position des Tors im Raum, so ist erkennbar, dass dieses so gewählt wurde, dass das Tor in der y,z-Ebene steht. Daraus folgt, dass die x-Koordinate des Treffpunkts immer gleich Null sein muss. Somit lässt sich die Ungleichung durch das Einsetzen von x = 0 noch einmal vereinfachen.
Zur Veranschaulichung soll ein Beispiel dienen: Die Bewegungsgeschwindigkeit des Torwarts soll auf 4 m/s festgelegt sein. Dann gilt für den Treffpunkt folgende Mindestgeschwindigkeit:
Das bedeutet, dass bei einem Treffer am Treffpunkt die Geschwindigkeit des Balles 63.43 km/h überschreiten muss, um sicherzustellen, dass der Torwart den Ball nicht mehr halten kann. Nutzt man nun aber für den Torwart eine andere Bewegungsgeschwindigkeit, im folgenden Beispiel 5 m/s, so ist zu erkennen, dass bei höherer Bewegungsgeschwindigkeit auch eine höhere Schussgeschwindigkeit erforderlich ist, um einen sicheren Treffer an einem beliebigen Treffpunkt gewährleisten zu können.
Außerdem soll nun noch betrachtet werden, was mit der Geschwindigkeit des Balles passiert, falls der Treffpunkt genau mit einem Punkt der Hände oder übereinstimmt. Dann würde mit für gelten, dass . Innerhalb des Modells soll aber < gelten und die Zeit ist im Bereich festgelegt. Dann ist aber die Ungleichung < nicht erfüllbar. In der Ungleichung wird dies auch dadurch deutlich, dass der Quotient Null ergibt und der Bruch somit nicht definiert ist.
Software
[Bearbeiten]Microsoft Excel
[Bearbeiten]In Zyklus zwei haben wir mit dem Tabellenkalkulationsprogramm "Microsoft Excel" die stochastischen Kenngrößen Erwartungswert, Varianz und Standardabweichung, sowie die Binomial- bzw. Normalverteilung bestimmt. Dazu haben wir zunächst eine Tabelle mit den bereits bekannten Daten Position, Schüsse und Wahrscheinlichkeit erstellt. Da der Erwartungswert bei unserem Zufallsexperiment gleich der jeweiligen Trefferzahl ist, konnten wir den Wert einfach übernehmen. Die Varianz mussten wir nur für einen Wert berechnen, indem wir die Formel in eine Zelle eingetragen haben. Anschließend konnten wir die Werte für alle anderen Positionen durch Ziehen der Maus angeben. Analog sind wir auch bei der Standardabweichung vorgegangen.

Für die Binomialverteilung mussten wir zunächst alle möglichen Trefferzahlen angeben, also 0 bis 201. Dabei muss man nicht jeden Wert einzeln angeben, sondern kann nach zwei eingegeben Werten die Zellen beliebig nach unten ziehen. Die Berechnung der einzelnen Werte läuft dann über die Excel-Funktion "BINOM.VERT(Zahl der Erfolge, Versuche, Erfolgswahrscheinlichkeit, Falsch)". Durch diese Funktion werden die einzelnen Werte für jede Trefferzahl angegeben. Analog geht man bei der Approximation der Binomialverteilung durch die Normalverteilung vor. Hier nimmt man die Excel-Funktion "NORM.VERT(Trefferzahl, Erwartungswert ± 0,5, Standardabweichung, Wahr). Um hier die Wahrscheinlichkeit für die einzelne und nicht die kumulierten Trefferzahl zu bestimmen muss man noch "NORM.VERT(Trefferzahl, Erwartungswert + 0,5, Standardabweichung, Wahr) - "NORM.VERT(Trefferzahl, Erwartungswert - 0,5, Standardabweichung, Wahr) bestimmen.
Um abschließend die Verteilungen als Grafik darzustellen, wählt man die Trefferzahlen und die Werte der Binomial- bzw. Normalverteilung aus und fügt sie als Diagramm ein.
GeoGebra
[Bearbeiten]GeoGebra wurde im zweiten Modellierungszyklus dazu genutzt, die Mittelpunkte der neun Felder und deren jeweiligen Abstand zum Elfmeterpunkt als Ausgangspunkt des Schusses zu bestimmen. Außerdem wurden die zwei Handpunkte des Torwarts modelliert und mithilfe dieser Grafik die Abstände zwischen dem Torwart und beliebiger Treffpunkte bestimmt. Die Grafiken wurden innerhalb des 3D-Grafik-Programm in GeoGebra durchgeführt. Zur Erzeugung der Grafiken in GeoGebra werden folgenden Funktionen über das Eingabefeld benötigt:
1. Erstellen eines Punktes
2. Erstellen einer Strecke
3. Mittelpunkt einer Strecke
oder
4. Erstellen eines Vielecks
5. Bestimmung Abstand zweier Punkte
6. Einfügen von Text
Ein Textfeld kann über die Auswahlliste oben links eingefügt werden. Wird das Feld „ABC“ ausgewählt, muss dann die gewünschte Stelle in der Grafik ausgewählt werden, bevor der Text eingegeben werden kann.
WXMaxima
[Bearbeiten]WXMaxima wurde dazu genutzt, die Rechnungen innerhalb der Gleichungen und Ungleichungen im zweiten Modellierungszyklus durchzuführen. WXMaxima vereinfacht die Rechnungen, indem zuvor die Komponenten des Treffpunkts im Tor definiert werden und dann jede Gleichung, die mit den eingesetzten Werten berechnet werden soll, durch Shift+Return erneut ausgeführt werden. Zum Verfassen der zu definierenden Komponenten und Gleichungen bzw. Ungleichungen wurden folgende Funktionen von WXMaxima verwendet:
1. Zuweisung eines Werts zu einer Variablen
Werte können einer Variablen zugeordnet werden, indem ":" genutzt wird. Beispielsweise wird bei "a:5" der Variablen a der Wert 5 zugeordnet und somit in allen weiteren Ausführungen mit der Variablen a als Wert 5 umgesetzt. Die Zuordnung kann im Nachhinein auch verändert werden und durch erneutes Ausführen der nachfolgenden Anweisungen übertragen werden.
2. Einsetzen von Variablen in Gleichungen
Wurden in vorherigen Anweisungen verschiedenen Variablen ein Wert zugeordnet, so können diese in nachfolgenden Anweisungen genutzt werden. Zur Aktualisierung von Änderungen ist ein erneutes Ausführen der Anweisung durch "Shift+Return" nötig.
3. Die Wurzelfunktion
Wurzeln können mit dem Ausdruck "sqrt(<Term>)" eingefügt werden.
4. Definition einer Matrix oder Spaltenvektoren
Matrizen und Spaltenvektoren können durch den Ausdruck "matrix([z11,z12],[z21,z22])" definiert werden. Dabei bildet die erste eckige Klammer die erste Zeile, ..., die n-te eckige Klammer die n-te Zeile. Spaltenvektoren können entsprechend so definiert werden, dass nur eine Komponente innerhalb einer eckigen Klammer steht.
5. if-Abfragen
Zur Aufstellung mancher Gleichungen und Ungleichungen innerhalb des zweiten Modellierungszyklus sind Fallunterscheidungen notwendig. Dies kann mit folgendem Ausdruck dargestellt werden: "if (<Bedingung>) then (<Befehle zur Ausführung bei erfüllter Bedingung>) elseif (<Bedingung>) then (<Bedingungen zur Ausführung bei erfüllter Bedingung>) else (<Befehle zur Ausführung bei nicht-erfüllter Bedingung>)". Der Teil "elseif(<Bedingung>)" ist nur optional zu wählen. Außerdem können weitere Bedingungen hinzugefügt werden.
Modellierungszyklus 3 - Niveau Uni
[Bearbeiten]Die im Modellierungszyklus 2 erarbeitete Formel für die zu überschreitende Geschwindigkeit des Balles für ein sicheres Tor an einem beliebigen Treffpunkt kann in diesem Abschnitt als Graph einer Funktion dargestellt werden. Da in dieser Formel allerdings nur die Merkmale Geschwindigkeit, Strecke und Zeit berücksichtigt wurde, können nun noch weitere Faktoren eingebaut werden. Das Ziel dieses Zyklus ist es also, eine Funktion als Graphen darzustellen, der die zu überschreitende Geschwindigkeit darstellt, in der allerdings auch übergeordnete Faktoren wie beispielsweise die Reaktionszeit des Torwarts, die Sprungkraft des Torwart oder die Winkelgeschwindigkeit der Armbewegung berücksichtigt werden sollen.


Anhand der dargestellten Funktionsgraphen ist ersichtlich, dass die zu überschreitende Geschwindigkeit vor allem im Bereich der Handpunkte schnell gegen unendlich streben. Außerdem ist eine Symmetrie zu erkennen, wobei die senkrechte Gerade durch die Mitte des Tors prinzipiell die Spiegelachse bildet. Das bedeutet, dass die Geschwindigkeiten, die überschritten werden müssen, im linken und rechten oberen Eck jeweils gleich sein müssen. Dies gilt generell für andere Punkte deren Komponenten betragsmäßig die jeweils gleiche Entfernung zu den Handpunkten des Torwarts aufweisen. Wie zu erwarten ist ebenfalls zu erkennen, dass die zu überschreitenden Geschwindigkeiten geringer werden, je weiter sie von den Handpunkten entfernt sind. Durch die entferntere Sicht auf den Graphen wird zudem deutlich, dass die Grenzwerte der Geschwindigkeit an den Handpunkten jeweils gegen unendlich streben.
Position der Hände abhängig von den Körpermaßen
[Bearbeiten]Im nächsten Schritt sollen die in Modellierungszyklus 2 festgelegten Handpunkte in Abhängigkeit von den Körpermaßen angegeben werden. Je nach Körpergröße und Körperbau (z.B. Breite der Hüfte) sind die Positionen der beiden Hände unterschiedlich. Dabei wird aber im Modell davon ausgegangen, dass die Torhüter ihre Hände dennoch vor dem Schuss auf Hüfthöhe neben dem Körper halten. Dann ergeben sich für und die folgenden Punkte:
Analog zu Modellierungszyklus 2 kommt also der Handpunkt zur Anwendung, wenn die y-Komponente des Treffpunkts kleiner oder gleich 3.66 ist. Der Handpunkt kommt zum Einsatz, wenn die y-Komponente des Treffpunkts größer als 3.66 ist. Daraus ergibt sich die folgende Formel zur Berechnung des Abstandes des Torwarts mit seinen Händen bis zum Treffpunkt:
Reaktionszeit des Torwarts
[Bearbeiten]Des Weiteren soll als Faktor die Reaktionszeit des Torwarts eine Rolle spielen. Im zweiten Modellierungszyklus wurde lediglich angenommen, dass der Torwart direkt während des Schusses seine Bewegung einleitet, aber dennoch nicht antizipiert, sondern reagiert. Zur Erweiterung des Modells soll deshalb die Reaktionszeit mit einbezogen werden. Sinnvoll ist es, die Reaktionszeit zur Zeit des Torwarts zu addieren, die er bis zum Treffpunkt benötigt, da er erst nach der Reaktion auf die Flugrichtung des Balles seine Bewegung einleiten kann. Somit gilt mit Bezug auf die in Modellierungszyklus 2 erarbeiteten Formeln:
Die Strecke des Torwarts bis zum Treffpunkt ist bekannt, wobei nun die in Zyklus 3 erarbeiteten Handpunkte bezüglich der Körpergröße eingesetzt werden müssen. Dann gilt folgendes:
Wird diese Zeit des Torwarts nun in die Ungleichung für die zu überschreitende Schussgeschwindigkeit für einen sicheren Treffer an einem beliebigen Treffpunkt eingesetzt, ergibt sich folgende Ungleichung:
<
Verfeinerung der Torwartbewegung als Translation und Rotation
[Bearbeiten]Außerdem soll die eigentliche Bewegung des Torwarts erneut betrachtet werden. Während in Zyklus 2 lediglich eine Translation der Handpunkte zu den jeweiligen Treffpunkten betrachtet wurde, soll in Zyklus 3 nun die Armbewegung genauer analysiert werden. Es handelt sich nämlich neben der Translation auch um eine Rotation um das rechte beziehungsweise linke Schultergelenk. Um nun die Entfernung und schließlich die Zeit des Torwarts zu berechnen, die notwendig zur Berechnung der verkomplizierten Ungleichung für sind, muss also die Mischung aus Translation und Rotation betrachtet werden. Dabei ist zunächst zu beachten, dass die Bewegungen nicht nacheinander, sondern gleichzeitig ausgeführt werden. Das bedeutet, dass der Torwart nicht erst seinen Arm im Schulterpunkt rotiert und dann in Richtung des Treffpunkts bewegt, sondern die Translation schon während der Rotation durchgeführt wird. Die Zeit, die der Torwart also insgesamt für die Bewegung braucht, ergibt sich aus dem Maximum der Translation und der Rotation. Benötigt der Torwart beispielsweise eine längere Zeit für die Translation, so wird die gesamte Rotation während der translatorischen Bewegung ausgeführt und spielt für die Zeit des Torwarts bis zum Treffpunkt keine Rolle mehr. Analog gilt dies, wenn die Rotation eine längere Zeit beansprucht als die Translation. Um das Maximum beider Bewegungen berechnen zu können, müssen die einzelnen Bewegungen beschrieben werden.
1. Translatorische Bewegung
Bezüglich der Translation ergibt sich nun ein neuer Bezugspunkt, um die Translation mit der Rotation verbinden zu können. Anstelle der Handpunkte wird nun von den Schultergelenken ausgegangen. Dabei sollen und wie folgt definiert werden:
Nun soll aber der Torwart den Ball dennoch mit den Händen halten. Betrachtet man dafür die Translation nach ausgeführter Rotation, so bilden die Punkte des Schultergelenks mit dem gleichseitigen Handpunkt die gleiche Gerade wie das Schultergelenk mit dem Treffpunkt. Das bedeutet, dass von der Strecke von Schultergelenk zu Treffpunkt noch die Strecke zwischen Schultergelenk und Hand subtrahiert werden muss, um die Strecke zu erhalten, die bei der Translation zurückgelegt wird. Dies soll mit der folgenden Abbildung verdeutlicht werden, wobei beispielhaft die Körpergröße 1.80m, die Hüftbreite 0.4m und eine Armlänge von 0.7m gewählt wurde:
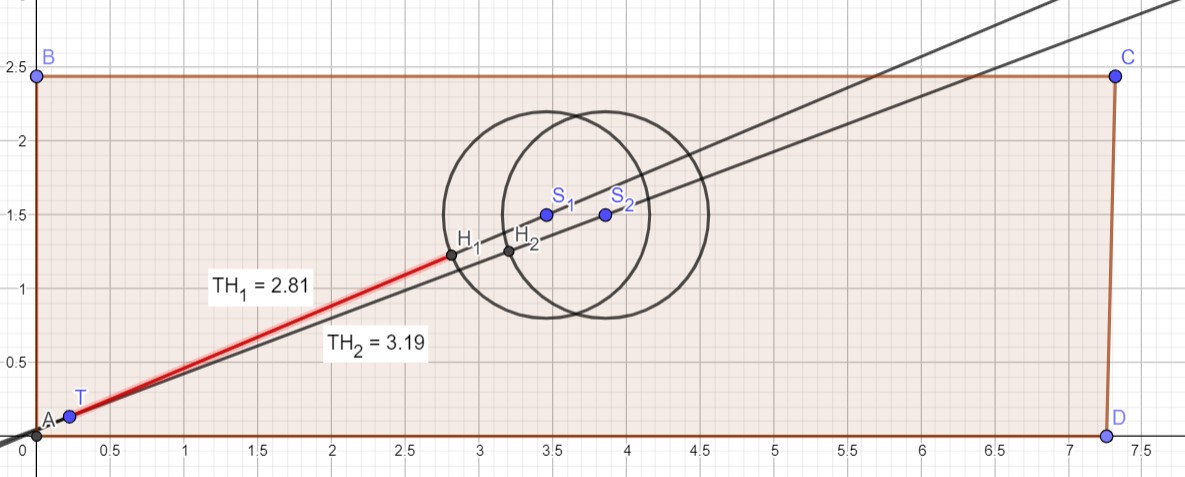
Dabei lässt sich die Entfernung, die er translatorisch zurücklegen muss wie folgt berechnen, wobei a die Armlänge des Torwarts darstellt:
Diese Formel kann wiederum in die Zeitformel eingesetzt werden, um im nachhinein das Maximum aus Translation und Rotation zu bestimmen:
2. Rotatorische Bewegung
Nun muss noch die Rotationsbewegung des Armes um das Schultergelenk beschrieben werden, um letztendlich das Maximum beider Bewegungen bezüglich der benötigten Zeit zum Treffpunkt berechnen zu können. Um die benötigte Zeit berechnen zu können, muss auch hier zunächst die zurückzulegende Strecke berechnet werden. Dabei wird bei Rotationsbewegungen der Winkel betrachtet, den der Arm überläuft. Generell gilt für Rotationsbewegungen:
, mit als Winkel, ω als Winkelgeschwindigkeit und t als Zeit
Der Winkel, den der Arm überschreiten muss, wird von den Strecken und , beziehungsweise und eingeschlossen. Mithilfe des Skalarprodukts kann berechnet werden:
Für die Zeit, die der Torwart für die Rotationsbewegung benötigt, gilt also:
3. Zeit, die der Torwart zum Treffpunkt benötigt
Die beiden vorherigen Formeln können nun in die Betrachtung des Maximums eingesetzt werden, um die Zeit zu bestimmen, die der Torwart bis zum Treffpunkt braucht. Die jeweilige Bewegung mit dem geringeren Zeitaufwand wird während der Bewegung mit höherem Zeitaufwand durchgeführt und bleibt somit bei der späteren Betrachtung der zu überschreitenden Schussgeschwindigkeit außenvor. Für die Zeit, die der Torwart bis zum Treffpunkt benötigt, gilt also:
4. Erweiterung Trefferpunkt in Handkreis
Befindet sich der Trefferpunkt innerhalb einer der Handkreise, so müssten wir nach unserem Modell eine Translation und eine Rotation ausführen. Da der/die Torhüter/in den Ball allerdings auch ohne eine Translation mit dem ausgestreckten Arm erreichen wird, beschränken wir die Bewegung des/der Torhüter/in in diesem Fall auf eine Rotation. Die Handkreise lassen sich wie folgt darstellen:
Daraus ergibt sich folgende Veränderung für :
5. Formel für die zur überschreitenden Geschwindigkeit mit den betrachteten Parametern
Die in Abschnitt eins bis vier betrachteten Parameter beeinflussen die gesuchte Schussgeschwindigkeit. Um die Formel dennoch etwas zu vereinfachen, sollen die Größenparameter des Torwarts in Abhängigkeit zur Körpergröße betrachtet werden. Außerdem soll die Körpergröße des Torwarts mit dem Parameter k beschrieben werden. Dabei sollen folgende Größenverhältnisse gelten:
Somit gilt für die zu überschreitende Schussgeschwindigkeit zu einem beliebigen Treffpunkt bezüglich der in Modellierungszyklus 2 erarbeiteten Ungleichung für und der in Modellierungszyklus 3 erarbeiteten Parametern:
Daraus ergibt sich, dass die obige Ungleichung für die zu überschreitende Geschwindigkeit von folgenden Parametern abhängig ist:
- Körpergröße des Torwarts
- Bewegungsgeschwindigkeit des Torwarts
- Winkelgeschwindigkeit der Arme des Torwarts
- Reaktionszeit des Torwarts
- Treffpunkt des Balles im Tor
Die Ungleichung soll nun als Funktion dargestellt werden, bei der das Tupel eingesetzt werden kann und als Funktionswert besitzt, wobei dabei gerade die Schussgeschwindigkeit angibt, bei der der Torwart und der Ball gleichzeitig am Treffpunkt ankommen. Es muss also gelten. Die Funktion kann wie folgt definiert werden:
Abgesehen vom Treffpunkt des Balles im Tor müssen zur Darstellung der Funktion im Koordinatensystem alle anderen Faktoren bekannt sein. Beispielhaft soll deshalb folgendes gelten:


Um die Einflüsse der vier Parameter darzustellen, sollen nun noch zwei Beispiele mit Einsetzen extremer Werte für diese dargestellt werden, bei denen einmal eine hohe Geschwindigkeit nötig ist und einmal eine nur geringe Geschwindigkeit:
Beispiel 1:

Beispiel 2:

Auswertung
[Bearbeiten]Ziel des dritten Modellierungszyklus war es Faktoren einzubauen, die im realen Vorgang von Bedeutung sind, in Zyklus 2 allerdings noch nicht berücksichtigt wurden. Dabei sollten die Körpergröße und die Bewegung des Torwarts weiter analysiert werden. Die beiden Graphen in Zyklus 3 weisen eine Ähnlichkeit auf. Im Bereich mittleren Bereich ist die zu überschreitende Schussgeschwindigkeit höher als in den Ecken. Außerdem ist erneut eine Symmetrie bezüglich der Mitte des Tors erkennbar. Durch die Beispiele ist auch erkennbar, wie sich die Parameter des Torwarts auf den Graphen auswirken. In Beispiel 1 wurden die Werte so gewählt, dass sehr hohe Geschwindigkeiten benötigt werden, um ein sicheres Tor an einem Treffpunkt garantieren zu können. Dabei handelt es sich teilweise um Geschwindigkeiten von 100 m/s (zentral des Tors sogar teilweise ein Vielfaches davon). Währenddessen wurden in Beispiel 2 Werte eingesetzt, die zu geringen Geschwindigkeiten führen. In den Ecken werden dabei nur etwa 6 m/s für ein sicheres Tor benötigt, was 21.6 km/h entspricht. Selbst ein "einfacher Pass" zum Mitspieler würde diese Geschwindigkeit überschreiten. Bezüglich der Parameter und ihrer Auswirkung auf die zu überschreitende Geschwindigkeit für ein sicheres Tor gelten letztendlich folgende Aussagen:
- je größer der Torwart ist, desto höher ist die zu überschreitende Geschwindigkeit
- je höher die Bewegungsgeschwindigkeit des Torwarts ist, desto höher ist zu überschreitende Geschwindigkeit
- je höher die Winkelgeschwindigkeit der Arme der Torwarts ist, desto höher ist die zu überschreitende Geschwindigkeit
- je geringer die Reaktionszeit des Torwarts ist, desto höher ist die zu überschreitende Geschwindigkeit
Software
[Bearbeiten]GeoGebra
Für Modellierungszyklus 3 wurde GeoGebra genutzt, um die Entfernungen des Torwarts zum Treffpunkt bei der Translationsbewegung darzustellen. Dabei wurde im Zweidimensionalen gearbeitet, da der Elfmeterpunkt in diesem Fall keine Rolle spielt und das Tor, der Torwart und der Treffpunkt auf einer Ebene liegen. Zunächst wurden die Schulterpunkte definiert und jeweils einen Kreis mit der Armlänge des Torwarts um die Schulterpunkte gezogen. Außerdem wurde ein Treffpunkt des Balles im Tor definiert. Um nun die Entfernung zu bestimmen, die der Torwart bei der Translationsbewegung zurücklegen muss, wurde jeweils eine Gerade durch den Treffpunkt und die beiden Schulterpunkte eingebaut. Da sich die Hände in einer Rotationsbewegung um den rechten bzw. linken Schulterpunkt Bewegen, liegen die Handpunkte stets auf der Kreislinie mit dem Radius der Armlänge. Somit ergeben sich die Handpunkte aus dem Schnittpunkt der Gerade und dem Kreis, die beide zum gleichen Schulterpunkt gehören. Der Abstand des Treffpunkts zu dem Schnittpunkt bildet dann die Entfernung, die der Torwart bei der Translationsbewegung zurücklegen muss. Dabei kann der Treffpunkt beliebig im Tor verschoben werden, während sich die Handpunkte und die Entfernungsberechnung entsprechend anpassen. Außerdem wurde zu Beginn des dritten Modellierungszyklus eine 3D-Grafik mit GeoGebra erstellt, wobei eine Fallunterscheidung und Begrenzung des Definitionsbereichs auf das Tor getätigt wurden. Folgende Funktionen wurden genutzt, um die Darstellung zu erstellen:
1. Erstellen eines Punktes
2. Erstellen einer Strecke
3. Erstellen eines Vielecks
4. Kreis mit Mittelpunkt und Radius
5. Erstellung einer Gerade durch zwei Punkte
6. Bestimmung Abstand zweier Punkte
7. Funktionsgraphen in 3D-Grafik
8. Bedingungen
9. Begrenzung des Definitionsbereichs
Die Begrenzung des Definitionsbereichs der Funktion wurde in die Bedingung der Fallunterscheidung und die Bedingung im Bereich <Sonst> für die Funktion eingebettet.
Innerhalb dieser GeoGebra-Darstellung wird ausgenutzt, dass Punkte beispielsweise bezüglich Schnittpunkten fixiert sind und sich bei Veränderung bestimmter Punkte, die auch beispielsweise den Schnittpunkt verändern, dann auch entsprechend verändern. So kann mit dieser Darstellung für jeden beliebigen Punkt im Tor der kürzeste Abstand der Handpunkte nach der Rotation auf der jeweiligen Kreisbahn bestimmt werden.
WXMaxima
WXMaxima wurde im dritten Modellierungszyklus genutzt, um die erarbeitete Funktion f im Raum darzustellen. Hierbei der Umstieg von GeoGebra auf WXMaxima, da es in WXMaxima leichter fällt, Funktionen mit mehreren Parametern zu definieren, wobei die Parameter durch erneutes Ausführen der Befehle zur Definition der Parameter direkt in die Funktionsgleichung übernommen werden können, wenn auch diese zur Aktualisierung erneut ausgeführt wird. Außerdem kann nach dem Plot des Funktionsgraphen eine Art Heatmap erzeugt werden, indem man den Graphen in der Ansicht auf Frontalansicht auf die horizontal liegende Ebene einstellt. Dadurch wird das Tor frontal besichtigt, wobei die verschiedenen Farben des Graphen dann die Heatmap erzeugen. Zur Erstellung des Graphen wurden folgende Funktionen von WXMaxima genutzt:
1. Zuweisung eines Werts zu einer Variablen
Werte können einer Variablen zugeordnet werden, indem ":" genutzt wird. Beispielsweise wird bei "a:5" der Variablen a der Wert 5 zugeordnet und somit in allen weiteren Ausführungen mit der Variablen a als Wert 5 umgesetzt. Die Zuordnung kann im Nachhinein auch verändert werden und durch erneutes Ausführen der nachfolgenden Anweisungen übertragen werden.
2. Einsetzen von Variablen in Gleichungen
Wurden in vorherigen Anweisungen verschiedenen Variablen ein Wert zugeordnet, so können diese in nachfolgenden Anweisungen genutzt werden. Zur Aktualisierung von Änderungen ist ein erneutes Ausführen der Anweisung durch "Shift+Return" nötig.
3. Die Wurzelfunktion
Wurzeln können mit dem Ausdruck "sqrt(<Term>)" eingefügt werden.
4. Die Maximumsfunktion
Das Maximum einer Liste von Zahlen kann durch "max(<Ausdruck 1>,...,<Ausdruck n>)" dargestellt werden.
5. Die Umkehrfunktion des Kosinus
Der arccos wird in WXMaxima mit "acos(.)" dargestellt.
6. if-Abfragen
Zur Aufstellung der Funktion des dritten Modellierungszyklus sind Fallunterscheidungen notwendig. Dies kann mit folgendem Ausdruck dargestellt werden:
"if (<Bedingung>) then (<Befehle zur Ausführung bei erfüllter Bedingung>) elseif (<Bedingung>) then (<Bedingungen zur Ausführung bei erfüllter Bedingung>) else (<Befehle zur Ausführung bei nicht-erfüllter Bedingung>)".
Der Teil "elseif(<Bedingung>)" ist nur optional zu wählen. Außerdem können weitere Bedingungen hinzugefügt werden.
7. Plotten einer 3D-Funktion
Das Plotten einer Funktion im Dreidimensionalen erfolgt mit:
"plot3d(<Term>,[erste Variable, Startwert, Endwert],[zweite Variable, Startwert, Endwert])"
Erscheint das Fenster mit dem Funktionsgraphen, kann das Koordinatensystem beliebig gedreht werden. Um die Heatmap darzustellen, muss das Koordinatensystem so gedreht werden, dass die Ansicht senkrecht auf die horizontale Ebene gerichtet ist.
Mathematische Theorie für die Modellierungszyklen
[Bearbeiten]Zyklus 1: Sekundarstufe I
[Bearbeiten]Mathematische Theorie
[Bearbeiten]Zufallsexperiment, Ergebnismenge, Ereignis
Als Zufallsexperiment wird ein realer Vorgang bezeichnet, bei dem die Durchführung unter festgelegten Bedingungen erfolgt, die Menge der möglichen Ergebnisse schon zuvor bekannt ist, das tatsächliche Ergebnis einer Durchführung allerdings nicht. Die Ergebnismenge, meist mit Omega bezeichnet, stellt dabei die Menge aller möglichen Ergebnisse des Zufallsexperiments dar, wobei bei jeder Durchführung dann auch genau eines der Elemente der Ergebnismenge eintritt. Bestimmte Teilmengen von Omega können als Ereignisse bezeichnet werden. Elementarereignisse beinhalten jeweils nur ein Element aus der Ergebnismenge, ganz Omega wird als sicheres Ereignis und die leere Menge wird als unmögliches Ereignis bezeichnet. Man sagt, dass ein Ereignis eintritt, wenn bei der Durchführung des Zufallsexperiments ein Ergebnis eintritt, das Element dieser Teilmenge ist. Bei einem Zufallsexperiment ist dann das Ziel, jedem Ereignis eine Wahrscheinlichkeit zuordnen zu können.
Absolute und relative Häufigkeit
Als absolute Häufigkeit eines Ereignisses A (kurz: ) wird die Anzahl der Durchführungen bezeichnet, bei denen das Ereignis A eingetreten ist. Dagegen stellt die relative Häufigkeit eines Ereignisses A (kurz: ) das Verhältnis aus der absoluten Häufigkeit und der Anzahl der Durchführungen dar. Es gilt also .
Empirisches Gesetz der großen Zahlen
Das Empirische Gesetz der großen Zahlen bezieht sich auf die relative Häufigkeit eines Ereignisses und sagt aus, dass sich die relative Häufigkeit bei wachsender Versuchszahl n stabilisiert. Dabei ist zu beachten, dass das Empirische Gesetz der großen Zahlen eine Erfahrungstatsache und nicht mathematisch beweisbar ist.
Zyklus 2: Sekundarstufe II
[Bearbeiten]Mathematische Theorie
[Bearbeiten]Binomialverteilte Zufallsvariable
[Bearbeiten]Eine binomialverteilte Zufallsvariable liegt vor, wenn ein Zufallsexperiment unabhängig voneinander und unter identischen Bedingungen n-mal durchgeführt wird. Die Zufallsvariable Z gibt hier die Anzahl der Versuche an, in denen ein bestimmtes Ereignis, dass die Wahrscheinlichkeit p hat, eintritt. Dabei ist die Bildmenge der Zufallsvariable abzählbar, da jedes Ereignis in einer natürlichen Zahl angegeben werden kann. Die Formel zur Berechnung der Wahrscheinlichkeit sieht wie folgt aus: n ∈ ℕ (Versuchszahl) und p ∈[0, 1] (Wahrscheinlichkeit), falls Z(Ω) = {0,…,n}:
P(Z = k) = •pk • (1-p)n-k für alle k ∈ {0,…,n}
Erwartungswert
[Bearbeiten]Der Erwartungswert einer binomialverteilten Zufallsvariabel mit Versuchszahl n ∈ ℕ und Trefferwahrscheinlichkeit p ∈ [0, 1] wird wie folgt ermittelt:
E (Z) = n • p
Dabei gibt der Erwartungswert die zu erwartende Trefferanzahl in Abhängigkeit der jeweiligen Trefferwahrscheinlichkeit und der Versuchszahl an.
Varianz
[Bearbeiten]Die Varianz einer binomialverteilten Zufallsvariabel mit Versuchszahl n ∈ ℕ und Trefferwahrscheinlichkeit p ∈ [0, 1] wird wie folgt ermittelt:
V (Z) = n • p • (1 - p)
Durch die Varianz wird die zu erwartende quadratische Abweichung vom Erwartungswert angegeben. Eine große Varianz sagt somit aus, dass viele Daten vom Erwartungswert abweichen. Man spricht dann von einer großen Streuung der Daten. Umgekehrt sagt eine kleine Varianz, dass die Werte nur in geringem Maß vom Erwartungswert abweichen. Die Daten haben also eine geringe Streuung.
Standardabweichung
[Bearbeiten]Um die Standardabweichung zu ermitteln, muss lediglich die Wurzel der Varianz berechnet werden. Die Formel lautet also:
σ(Z)= ∈[0, ∞)
Die Standardabweichung einer binomialverteilten Zufallsvariabel ist ein Streumaß, das Auskunft über die zu erwartenden Abweichungen vom Erwartungswert gibt. Durch das Ziehen der Wurzel wird das Quadrieren aus der Berechnung der Varianz (Standardformel zur Berechnung der Varianz: V(Z) := E( (Z - E(Z))2 ) ∈[0, ∞) ) ausgeglichen.
Approximation der Binomialverteilung durch die Normalverteilung
[Bearbeiten]Um praktische Regeln der Normalverteilung nutzen zu können, kann man eine binomialverteilte Zufallsvariable mit Versuchszahl n ∈ ℕ und Trefferwahrscheinlichkeit p ∈ [0, 1] durch die Normalverteilung approximieren. Für ein "großes" n gilt dann für alle k, l ∈ {1,…,n-1} mit k ≤ l:
P(X=l) ≈ Φ - Φ
Als Faustregel gilt hier, dass dies bei n•p•(1-p) = V(x) ≥ 9 in der Praxis eine ausreichend gute Näherung ist.
σ-Regeln der Normalverteilung
[Bearbeiten]Für μ = Erwartungswert und σ = Standardabweichung gilt:
P (|Z-μ| ≤ σ) = 2•Φ()-1 ≈ 0.3829 P (|Z-μ| ≤ σ) = 2•Φ(1) - 1 ≈ 0.6827 P (|Z-μ| ≤ 2•σ) = 2•Φ(2) - 1 ≈ 0.9545 P (|Z-μ| ≤ 3•σ) = 2•Φ(3) - 1 ≈ 0.9973
Durch die σ-Regeln kann man die Wahrscheinlichkeiten für bestimmte Ereignisse angeben, die in einem σ-Intervall vom Erwartungswert entfernt liegen. Geht man zum Beispiel vom Erwartungswert eine Standardabweichung nach rechts und eine nach links, liegt die Wahrscheinlichkeit für alle Werte in diesem σ-Intervall bei ungefähr 68,27 %.
Punkte im Koordinatensystem
[Bearbeiten]Mithilfe eines Koordinatensystems können Punkte in der Ebene oder im Raum eindeutig beschrieben werden. Bei Punkten im Raum sind drei Koordinaten erforderlich. Somit ergibt sich ein Punkt im Raum mit folgender Schreibweise: P(x|y|z), wobei x die Koordinate bzgl. der x-Achse, y die Koordinate bzgl. der y-Achse und z die Koordinate bzgl. der z-Achse angibt. Jeder Punkt ist also durch seine Komponenten eindeutig bestimmt.
Vektoren im Raum
[Bearbeiten]Vektoren können dazu verwendet werden, Punkte in einem Koordinatensystem zu beschreiben und das Rechnen, z.B. den Abstand zweier Punkte, zu ermöglichen. Um einen Punkt in einem Koordinatensystem mittels Vektors angeben zu können, werden Ortsvektoren benötigt. Mithilfe des Ortsvektors , wobei O(0|0|0) gilt, kann dann also der Punkt P angegeben werden. Vektoren im können durch ein Zahlentripel angegeben werden. Dieser Ausdruck wird auch als Spaltenvektor bezeichnet. Wie in der gewählten Schreibweise schon erkennbar ist, bildet die erste Komponente des Tripels die x-Koordinate, die zweite die y-Koordinate und die dritte Komponente bildet die z-Koordinate.
Rechnen mit Vektoren
[Bearbeiten]Addition und Subtraktion
Vektoren können addiert werden, indem sie hintereinander ausgeführt werden, wodurch sich ein Vektorzug bildet. In der Schreibweise mit Spaltenvektoren bedeutet dies eine komponentenweise Addition:
.
Die Subtraktion funktioniert ähnlich, wobei hier beispielsweise und miteinander addiert werden, da gilt. Auch die Subtraktion wird also komponentenweise durchgeführt:
.
Betrag eines Vektors Der Betrag eines Vektors gibt seine Länge an und kann mit folgender Formel berechnet werden:
Mithilfe dieser Formel kann auch der Abstand zwischen zwei Punkten berechnet werden. Die Strecke zwischen zwei Punkten P und Q kann durch einen Vektor ausgedrückt werden, indem beide Ortsvektoren und subtrahiert werden, das heißt:
,
daraus folgt dann die Betragsformel für den Abstand zweier Punkte:
Physikalische Grundlagen: Gleichförmige Bewegung
[Bearbeiten]Zunächst wird davon ausgegangen, dass es sich bei beiden Bewegungen um gleichförmige Bewegungen handelt, also eine Bewegung mit gleichbleibender Geschwindigkeit und gleichbleibender Richtung. Dabei gilt, dass in der gleichen Zeit immer die gleiche Strecke zurückgelegt wird, da die Geschwindigkeit konstant bleibt. Für die Zeit und die Strecke wird dabei jeweils ein Zeitintervall, z.B. 10 Sekunden, und für die Strecke eine Distanz, z.B. 30 Meter, angegeben. Daraus ergibt sich die folgende Gleichung:
Das Minimum zweier Zahlen
[Bearbeiten]Die Funktion gibt das kleineste Element einer Menge an. Somit gilt
, , .
Zyklus 3: Uni-Niveau
[Bearbeiten]Funktionsgraphen im dreidimensionalen Raum
Allgemein sind Funktionen Beziehungen zwischen zwei Mengen. Bei den beiden Mengen handelt es sich um Definitionsmenge und Wertemenge, wobei jedem Elemente aus der Definitionsmenge mithilfe der Funktionsvorschrift genau ein Element der Wertemenge zugeordnet wird. In Zyklus 3 handelt es sich um eine Funktion, die von auf abgebildet wird. Das bedeutet, dass jedem Tupel eine reelle Zahl zugeordnet wird. Allerdings wird in diesem Fall nicht ganz betrachtet, sondern nur eine Teilmenge . Das heißt, dass gilt: und . Solche Funktionen können in einem Koordinatensystem dargestellt werden. In diesem Fall wird ein dreidimensionales Koordinatensystem genutzt, wobei eine Stelle auf der horizontalen Ebene darstellen und die Höhe des Punktes, der senkrecht über dieser Stelle auf dem Funktionsgraph liegt, bildet den dem Tupel zugeordneten Funktionswert. So ergeben sich verschiedene Graphen, die zum Teil einem Gebirge ähneln.
Translationsbewegungen
Translationsbewegungen werden auch lineare Bewegungen genannt und beschreiben Bewegungen, bei denen alle Punkte eines physikalischen Systems, in diesem Modell der Körper des Torwarts, die gleiche Verschiebung erfahren. Es gibt verschiedene Arten von Translationen. Im Modell wird die gleichförmige Bewegung betrachtet. Diese wurde schon in Modellierungszyklus 2 erläutert. Es gilt also auch hier .
Rotationsbewegungen
Das Gegenstück zur Translation bildet die Rotation. Während bei Translationen die Punkte auf einer Linie verschoben werden, bewegen sie sich bei einer Rotationsbewegung im Kreis um ein Drehzentrum. Im Vergleich zur Translation überlaufen die Punkte keine Strecke, sondern einen Winkel. Damit lässt sich die sogenannte Winkelgeschwindigkeit wie folgt beschreiben: .
Skalarprodukt
Mithilfe des Skalarprodukts zweier Vektoren kann der zu überschreitende Winkel berechnet werden, den der Arm bei der Rotationsbewegung zurücklegt. Generell wird zwei Vektoren beim Anwenden des Skalarprodukts eine Zahl zugeordnet. Geometrisch gilt . Nach Umstellung der Gleichung zur Berechnung des Winkels gilt dann . Mithilfe dieser Gleichung kann dann durch die beiden Vektoren, die sich aus dem Schulterpunkt und dem Treffpunkt beziehungsweise dem Schulterpunkt und dem Handpunkt ergibt, den Winkel berechnen, den der Arm bei der Rotationsbewegung zurücklegt.
Maximum zweier Zahlen
Die Funktion gibt das größte Element einer Menge an. Somit gilt
, , .
Bewertung des Modells
[Bearbeiten]Zielerfüllung
[Bearbeiten]Das Ziel der Modellierung war zu Beginn, die Grundlagen des Elfmeterschießens und der mathematische Zusammenhang zu diesem darzustellen. Die Wahrscheinlichkeit ist dabei wohl das klassischste Beispiel. So konnte in Zyklus 1 die theoretisch angelegte Wahrscheinlichkeit für einen Torerfolg beim Elfmeterschießen von etwa 70% mithilfe des eigens durchgeführten Experiments bestätigt werden. Dabei sind leichte Abweichungen durch unterschiedliche beeinflussende Parameter, wie beispielsweise die Ermüdung nach einer gewissen Schussanzahl, möglich. Dennoch wurde durch das Modell die Wahrscheinlichkeit für einen Torerfolg bestätigt. Außerdem konnte schon durch einen leicht durchzuführenden Versuch gezeigt werden, dass die Trefferwahrscheinlichkeit in den Ecken, weiter vom Torwart entfernt, größer ist als in der Mitte. Ebenso werden die unteren Ecken als sicherer angesehen als die oberen, was wohl mit der Schusspräzision erklärbar ist.
Dennoch wurde im Laufe des zweiten Zyklus nicht mehr die Wahrscheinlichkeit für einen Treffer betrachtet, sondern die zu überschreitende Geschwindigkeit für ein sicheres Tor bezüglich eines Treffpunkts. Die Wahrscheinlichkeit ist zwar für die Statistik interessant und kann auch den Schützen bei der Entscheidungsfindung helfen, ob der Ball beim nächsten Elfmeter jedoch im Tor landet, kann durch die Wahrscheinlichkeit nicht vorhergesagt werden. Deshalb sollte eine grifffeste Größe betrachtet werden, die in Abhängigkeit des Treffpunkts aussagen kann, ob der Ball im Tor landen wird oder ob der Torwart den Ball halten kann. Die betrachtete Größe ist eben diese zu überschreitende Geschwindigkeit. Wie zu Beginn der Arbeit vermutet, ist die nötige Geschwindigkeit in den Ecken geringer als in der Nähe des Torwarts, da dieser eine größere Strecke zurücklegen muss, um den Ball zu halten.
In der Betrachtung der Realsituation soll nun erläutert werden, was das erarbeitete Modell für den realen Prozess des Elfmeterschießens bedeutet.
Betrachtung der Realsituation
[Bearbeiten]In beiden Graphen, die die Geschwindigkeit darstellen, bei der der Torwart den Ball gerade noch halten kann, ist zu erkennen, dass die Geschwindigkeit des Balles in den Ecken sehr gering ist. Oft tatsächlich auch geringer als die tatsächliche Schussgeschwindigkeit bei einem Elfmeter, die im Schnitt je nach Spielklasse bei 80-100km/h liegt. Teilweise werden aber nur 50 km/h für einen unhaltbaren Schuss benötigt. Dadurch wird ersichtlich, dass der Torwart in einer Elfmetersituation kaum eine Chance hat einen Ball zu halten, wenn er versucht auf den Schuss zu reagieren. Viele Torhüter nutzen deswegen ihre Antizipationsfähigkeit aus, um die Schussrichtung vorherzusagen und vor der eigenen Reaktion die Bewegung einzuleiten. Andererseits nutzen dies auch viele Schützen aus, um den Torwart sozusagen "auszugucken" und zu erkennen wo er hinspringt. Allein durch diese Beschreibung ist erkennbar, dass sich hinter einem Elfmeterschießen viel mehr verbirgt als der Treffpunkt, die Geschwindigkeit und Reaktionszeit des Torwarts. Dennoch werden oft sehr platzierte Schüsse in die unteren oder oberen Ecken mit einer hohen Schussgeschwindigkeit als unhaltbar bezeichnet, da der Torwart viel zu früh seine Bewegung in die Schussrichtung einleiten müsste, um den Ball zu halten. Ein guter Schütze erkennt dies und kann ohne Probleme in die andere Ecke schießen. Vor allem für den Torwart ist dabei ein Abwägen von Reaktion auf die tatsächliche Schussrichtung und Antizipation durch Vorerfahrung oder Körpersprache des Schützen notwendig, um den Ball halten zu können. Für den Schützen gilt, dass ein fester und sehr platzierter Schuss als unhaltbar gewertet werden kann. Auch wenn der Torwart die Ecke ahnt. Anhand der Betrachtung der Realsituation ist erkennbar, dass weit mehr Faktoren eine Rolle im Elfmeterschießen spielen. Welche dabei das Modell noch erweitern können oder sogar sehr stark verändern würden, soll im Abschnitt Probleme des Modells geklärt werden.
Probleme des Modells: Optimierungsmöglichkeiten und Ausblick
[Bearbeiten]Das erarbeitete Modell kann die Grundlage zur Erweiterung der Elfmetermodellierung darstellen, da einige Faktoren unberücksichtigt bleiben, die allerdings durch einen weiteren Optimierungszyklus hinzugefügt werden können. Zunächst wurde in den Zyklen stets betrachtet, dass der Torwart auf die Schussrichtung reagiert. Wie im Abschnitt Realsituation allerdings schon beschrieben wurde, ist der Torwart bei Reaktion auf die Schussrichtung meist chancenlos, weshalb er den Treffpunkt des Balles versucht zu antizipieren. Das heißt, er würde seine Bewegung schon vor der Schussausführung einleiten, wodurch sich die Zeit des Torwarts bis zum Treffpunkt ändern würde. Außerdem besteht die Möglichkeit, dass sich der Torwart für die falsche Ecke entscheidet. Des Weiteren wurde nicht berücksichtigt, was bei einem Schuss auf die Körperfläche des Torwarts passiert. Generell würde er innerhalb des Modells wohl stehen bleiben, weshalb es hier sicher nicht zu einem Torerfolg kommt, allerdings besteht hier erneut die Frage nach der Antizipation, wenn er also zuvor in eine Ecke springt und der Schütze in die Mitte schießen kann. Durch die verfrühte Einleitung der Bewegung ist auch ein "Ausgucken" des Torwarts für den Schützen möglich. Ebenso wird die Reaktionszeit immer zur Zeit der Torwartbewegung bis zum Treffpunkt addiert. Deshalb kommt es bei der Funktion am Ende des dritten Modellierungszyklus nicht mehr zu einem Streben ins Unendliche in der unmittelbaren Nähe der Handpunkte. Wenn der Schütze aber genau auf die Handpunkte schießt, könnte der Torwart den Ball auch ohne eine Reaktion des Ball halten, da er sich nicht bewegen müsste. Eine solche Differenzierung könnte das Modell zusätzlich optimieren. Die Torwartbewegung könnte ebenfalls weiter verfeinert werden. Beispielsweise wirken sich seine Explosivkraft in Form seiner Sprungkraft und sein Körpergewicht auf die Bewegungsgeschwindigkeit innerhalb der Translationsbewegung aus. Außerdem wurde im Modell lediglich berücksichtigt, dass der Torwart den Ball mit seinen Händen hält, wobei auch ein Halten mit anderen Körperteilen möglich ist. Auch der Schütze kann das Modell beeinflussen. Dabei kann betrachtet werden, inwiefern sich die Schusstechnik, also ein Schuss mit der Innenseite, der Außenseite oder ein Vollspannstoß auf die nötige Geschwindigkeit auswirkt. Die verschiedenen Schusstechniken können beispielweise eine Kurve im Schuss oder einen sogenannten "Flatterball" erzeugen. Die Auswirkung solcher Flugkurven auf einer kurzen Distanz können ebenso berücksichtigt werden wie der Fuß, mit dem der Schütze schießt. Oft wird für einen Rechtsfuß die untere linke Ecke als sicherer gehandelt als die rechte untere Ecke. Eine Begründung dafür könnte das Modell ebenfalls erweitern. Betrachtet man die Elfmeter der Profifußballer, sind weitere spektakuläre Elfmetervarianten erkennbar. Innerhalb des Modells wurden die Bewegungen außerdem als gleichförmige Bewegungen betrachtet, wobei die Geschwindigkeit eine Konstante ist. Allerdings werden beide Bewegungen, die des Balles und die des Torwarts, zunächst beschleunigt, durch Schussausführung bzw. den Sprung, und dann durch den Luftwiderstand leicht abgebremst. Das bedeutet, dass die Wirkungen der Beschleunigungen nicht berücksichtigt wurden. Zuletzt muss die Abhängigkeit von Schussgeschwindigkeit und Präzision betrachtet werden. Wenn ein Ball mit größerer Krafteinwirkung geschossen wird, leidet meist die Präzision darunter. Das bedeutet, je schneller der Ball in Richtung Tor fliegt, desto höher ist Ungenauigkeit bezüglich des gewählten Treffpunkts. Die Modellierung dieses Faktors wäre ein weiterer Punkt, wie das Modell optimiert bzw. erweitert werden kann.
Quellen/Literatur
[Bearbeiten]• https://iba.online/raeume-planen/flachenplanung/koerpermasse/


















![{\displaystyle |TWzuTP|=min({\overline {TH_{1}}},{\overline {TH_{2}}})={\begin{cases}{\Bigg |}{\begin{pmatrix}0\\3.41\\1\end{pmatrix}}-{\begin{pmatrix}x\\y\\z\end{pmatrix}}{\Bigg |}&{\text{wenn }}y\leq 3.66\\[3pt]{\Bigg |}{\begin{pmatrix}0\\3.91\\1\end{pmatrix}}-{\begin{pmatrix}x\\y\\z\end{pmatrix}}{\Bigg |}&{\text{wenn }}y>3.66\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13056a0ef5bd3540a56a5c3fe87beb15a28cd46e)

![{\displaystyle t_{Torwart}={\tfrac {s_{Torwart}}{v_{Torwart}}}={\tfrac {|TWzuTP|}{v_{Torwart}}}{\begin{cases}{\Bigg |}{\tfrac {{\begin{pmatrix}0\\3.41\\1\end{pmatrix}}-{\begin{pmatrix}x\\y\\z\end{pmatrix}}}{4}}{\Bigg |}&{\text{wenn }}y\leq 3.66\\[3pt]{\Bigg |}{\tfrac {{\begin{pmatrix}0\\3.91\\1\end{pmatrix}}-{\begin{pmatrix}x\\y\\z\end{pmatrix}}}{4}}{\Bigg |}&{\text{wenn }}y>3.66\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1684613ee38aefbeeb54ae28a3d586826e81ae92)

![{\displaystyle t_{Torwart}={\tfrac {s_{Torwart}}{v_{Torwart}}}={\tfrac {|TWzuTP|}{v_{Torwart}}}{\begin{cases}{\Bigg |}{\tfrac {{\begin{pmatrix}0\\3.41\\1\end{pmatrix}}-{\begin{pmatrix}x\\y\\z\end{pmatrix}}}{v_{Torwart}}}{\Bigg |}&{\text{wenn }}y\leq 3.66\\[3pt]{\Bigg |}{\tfrac {{\begin{pmatrix}0\\3.91\\1\end{pmatrix}}-{\begin{pmatrix}x\\y\\z\end{pmatrix}}}{v_{Torwart}}}{\Bigg |}&{\text{wenn }}y>3.66\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed975d7a3a954aa568fc03309fbba743ffdbc1d2)


![{\displaystyle t_{Torwart}\;\!\iff {\tfrac {s_{Ball}}{v_{Ball}}}<{\tfrac {s_{Torwart}}{v_{Torwart}}}\;\!\iff v_{Ball}>{\tfrac {s_{Ball}}{\tfrac {s_{Torwart}}{v_{Torwart}}}}\;\!\iff v_{Ball}>{\begin{cases}{\tfrac {\sqrt {(11-x)^{2}+(3.66-y)^{2}+(0-z)^{2}}}{\tfrac {\sqrt {(0-x)^{2}+(3.41-y)^{2}+(1-z)^{2}}}{v_{Torwart}}}}&{\text{wenn }}y\leq 3.66\\[3pt]{\tfrac {\sqrt {(11-x)^{2}+(3.66-y)^{2}+(0-z)^{2}}}{\tfrac {\sqrt {(0-x)^{2}+(3.91-y)^{2}+(1-z)^{2}}}{v_{Torwart}}}}&{\text{wenn }}y>3.66\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a6372ee7d3e234ca9aa6eae6838375f9344fbe9)
![{\displaystyle v_{Ball}>{\begin{cases}{\tfrac {\sqrt {11^{2}+(3.66-y)^{2}+(0-z)^{2}}}{\tfrac {\sqrt {(3.41-y)^{2}+(1-z)^{2}}}{v_{Torwart}}}}&{\text{wenn }}y\leq 3.66\\[3pt]{\tfrac {\sqrt {11^{2}+(3.66-y)^{2}+(0-z)^{2}}}{\tfrac {\sqrt {(3.91-y)^{2}+(1-z)^{2}}}{v_{Torwart}}}}&{\text{wenn }}y>3.66\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f09fa6d565bf9b6aef77610be378684265347fb)















![{\displaystyle s_{Torwart}=|TWzuTP|=min({\overline {TH_{1}}},{\overline {TH_{2}}})={\begin{cases}{\Bigg |}{\begin{pmatrix}0\\3.66-({\tfrac {b_{\text{Hüfte}}}{2}}+0.1)\\h_{Schritt}\end{pmatrix}}-{\begin{pmatrix}x\\y\\z\end{pmatrix}}{\Bigg |}&{\text{wenn }}y\leq 3.66\\[3pt]{\Bigg |}{\begin{pmatrix}0\\3.66+({\tfrac {b_{\text{Hüfte}}}{2}}+0.1)\\h_{Schritt}\end{pmatrix}}-{\begin{pmatrix}x\\y\\z\end{pmatrix}}{\Bigg |}&{\text{wenn }}y>3.66\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc27c01c961c540eda9b48a03383cf78d47100fe)
![{\displaystyle ={\begin{cases}{\sqrt {(3.66-({\tfrac {b_{\text{Hüfte}}}{2}}+0.1)-y)^{2}+(h_{Schritt}-z)^{2}}}&{\text{wenn }}y\leq 3.66\\[3pt]{\sqrt {(3.66+({\tfrac {b_{\text{Hüfte}}}{2}}+0.1)-y)^{2}+(h_{Schritt}-z)^{2}}}&{\text{wenn }}y>3.66\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/729dfca4a666bfc52de5d8eb42dcb321d2b894c6)

![{\displaystyle t_{Torwart}={\tfrac {s_{Torwart}}{v_{Torwart}}}+t_{Reaktion}={\tfrac {|TWzuTP|}{v_{Torwart}}}+t_{Reaktion}={\begin{cases}{\tfrac {\sqrt {(3.66-({\tfrac {b_{\text{Hüfte}}}{2}}+0.1)-y)^{2}+(h_{Schritt}-z)^{2}}}{v_{Torwart}}}+t_{Reaktion}&{\text{wenn }}y\leq 3.66\\[3pt]{\tfrac {\sqrt {(3.66+({\tfrac {b_{\text{Hüfte}}}{2}}+0.1)-y)^{2}+(h_{Schritt}-z)^{2}}}{v_{Torwart}}}+t_{Reaktion}&{\text{wenn }}y>3.66\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5b429b0102a630f18b8562a437dc43cc597c95d)

![{\displaystyle \;\!\iff v_{Ball}>{\begin{cases}{\tfrac {\sqrt {11^{2}+(3.66-y)^{2}+z^{2}}}{{\tfrac {\sqrt {(3.66-({\tfrac {b_{\text{Hüfte}}}{2}}+0.1)-y)^{2}+(h_{Schritt}-z)^{2}}}{v_{Torwart}}}+t_{Reaktion}}}&{\text{wenn }}y\leq 3.66\\[3pt]{\tfrac {\sqrt {11^{2}+(3.66-y)^{2}+z^{2}}}{{\tfrac {\sqrt {(3.66+({\tfrac {b_{\text{Hüfte}}}{2}}+0.1)-y)^{2}+(h_{Schritt}-z)^{2}}}{v_{Torwart}}}+t_{Reaktion}}}&{\text{wenn }}y>3.66\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b2616ac9218793ce369e11ac6e65877c9b203d8)





![{\displaystyle s_{Translation}=|TH_{1}|=|TS_{1}|-a={\begin{cases}{\sqrt {(3.66-{\tfrac {b_{\text{Hüfte}}}{2}}-y)^{2}+(h_{\text{Körper}}-0.3-z)^{2}}}-a&{\text{wenn }}y\leq 3.66\\[3pt]{\sqrt {(3.66+{\tfrac {b_{\text{Hüfte}}}{2}}-y)^{2}+(h_{\text{Körper}}-0.3-z)^{2}}}-a&{\text{wenn }}y>3.66\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/455cfd4fea466beb9f964a70d6b48b6c73862474)
![{\displaystyle t_{Translation}={\begin{cases}{\tfrac {{\sqrt {(3.66-{\tfrac {b_{\text{Hüfte}}}{2}}-y)^{2}+(h_{\text{Körper}}-0.3-z)^{2}}}-a}{v_{Torwart}}}+t_{Reaktion}&{\text{wenn }}y\leq 3.66\\[3pt]{\tfrac {{\sqrt {(3.66+{\tfrac {b_{\text{Hüfte}}}{2}}-y)^{2}+(h_{\text{Körper}}-0.3-z)^{2}}}-a}{v_{Torwart}}}+t_{Reaktion}&{\text{wenn }}y>3.66\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c3c7e2b753872eee0ec17af17537581750955af)







![{\displaystyle \varphi ={\begin{cases}arccos{\tfrac {S_{1}T\cdot S_{1}H_{1}}{|S_{1}T|\cdot |S_{1}H_{1}|}}&{\text{wenn }}y\leq 3.66\\[3pt]arccos{\tfrac {S_{2}T\cdot S_{2}H_{2}}{|S_{2}T|\cdot |S_{2}H_{2}|}}&{\text{wenn }}y>3.66\end{cases}}={\begin{cases}arccos{\tfrac {{\Bigg (}{\begin{pmatrix}0\\3.66-{\tfrac {b_{\text{Hüfte}}}{2}}\\h_{\text{Körper}}-0.3\end{pmatrix}}-{\begin{pmatrix}0\\y\\z\end{pmatrix}}{\Bigg )}\cdot {\Bigg (}{\begin{pmatrix}0\\3.66-{\tfrac {b_{\text{Hüfte}}}{2}}\\h_{\text{Körper}}-0.3\end{pmatrix}}-{\begin{pmatrix}0\\3.66-b_{\text{Hüfte}}\\h_{Schritt}\end{pmatrix}}{\Bigg )}}{{\Bigg |}{\begin{pmatrix}0\\3.66-{\tfrac {b_{\text{Hüfte}}}{2}}\\h_{\text{Körper}}-0.3\end{pmatrix}}-{\begin{pmatrix}0\\y\\z\end{pmatrix}}{\Bigg |}\cdot {\Bigg |}{\begin{pmatrix}0\\3.66-{\tfrac {b_{\text{Hüfte}}}{2}}\\h_{\text{Körper}}-0.3\end{pmatrix}}-{\begin{pmatrix}0\\3.66-b_{\text{Hüfte}}\\h_{Schritt}\end{pmatrix}}{\Bigg |}}}&{\text{wenn }}y\leq 3.66\\[3pt]arccos{\tfrac {{\Bigg (}{\begin{pmatrix}0\\3.66+{\tfrac {b_{\text{Hüfte}}}{2}}\\h_{\text{Körper}}-0.3\end{pmatrix}}-{\begin{pmatrix}0\\y\\z\end{pmatrix}}{\Bigg )}\cdot {\Bigg (}{\begin{pmatrix}0\\3.66+{\tfrac {b_{\text{Hüfte}}}{2}}\\h_{\text{Körper}}-0.3\end{pmatrix}}-{\begin{pmatrix}0\\3.66+b_{\text{Hüfte}}\\h_{Schritt}\end{pmatrix}}{\Bigg )}}{{\Bigg |}{\begin{pmatrix}0\\3.66+{\tfrac {b_{\text{Hüfte}}}{2}}\\h_{\text{Körper}}-0.3\end{pmatrix}}-{\begin{pmatrix}0\\y\\z\end{pmatrix}}{\Bigg |}\cdot {\Bigg |}{\begin{pmatrix}0\\3.66+{\tfrac {b_{\text{Hüfte}}}{2}}\\h_{\text{Körper}}-0.3\end{pmatrix}}-{\begin{pmatrix}0\\3.66+b_{\text{Hüfte}}\\h_{Schritt}\end{pmatrix}}{\Bigg |}}}&{\text{wenn }}y>3.66\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/477aa12b99e0ca028146e0e4814c00b3a7127d4d)
![{\displaystyle ={\begin{cases}arccos{\tfrac {(3.66-{\tfrac {b_{\text{Hüfte}}}{2}}-y)\cdot (-{\tfrac {3b_{\text{Hüfte}}}{2}})+(h_{\text{Körper}}-0.3-z)\cdot (h_{\text{Körper}}-0.3-h_{Schritt})}{{\sqrt {(3.66-{\tfrac {b_{\text{Hüfte}}}{2}}-y)^{2}+(h_{\text{Körper}}-0.3-z)^{2}}}\cdot {\sqrt {(-{\tfrac {3b_{\text{Hüfte}}}{2}})^{2}+(h_{\text{Körper}}-0.3-h_{Schritt})}}}}&{\text{wenn }}y\leq 3.66\\[3pt]arccos{\tfrac {(3.66+{\tfrac {b_{\text{Hüfte}}}{2}}-y)\cdot ({\tfrac {3b_{\text{Hüfte}}}{2}})+(h_{\text{Körper}}-0.3-z)\cdot (h_{\text{Körper}}-0.3-h_{Schritt})}{{\sqrt {(3.66+{\tfrac {b_{\text{Hüfte}}}{2}}-y)^{2}+(h_{\text{Körper}}-0.3-z)^{2}}}\cdot {\sqrt {({\tfrac {3b_{\text{Hüfte}}}{2}})^{2}+(h_{\text{Körper}}-0.3-h_{Schritt})}}}}&{\text{wenn }}y>3.66\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f771fb3bd6fe97c8f7fe63dbcb3b32a999b829a8)
![{\displaystyle t_{Rotation}={\begin{cases}{\tfrac {arccos{\tfrac {(3.66-{\tfrac {b_{\text{Hüfte}}}{2}}-y)\cdot (-{\tfrac {3b_{\text{Hüfte}}}{2}})+(h_{\text{Körper}}-0.3-z)\cdot (h_{\text{Körper}}-0.3-h_{Schritt})}{{\sqrt {(3.66-{\tfrac {b_{\text{Hüfte}}}{2}}-y)^{2}+(h_{\text{Körper}}-0.3-z)^{2}}}\cdot {\sqrt {(-{\tfrac {3b_{\text{Hüfte}}}{2}})^{2}+(h_{\text{Körper}}-0.3-h_{Schritt})}}}}}{\text{ω}}}+t_{Reaktion}&{\text{wenn }}y\leq 3.66\\[3pt]{\tfrac {arccos{\tfrac {(3.66+{\tfrac {b_{\text{Hüfte}}}{2}}-y)\cdot ({\tfrac {3b_{\text{Hüfte}}}{2}})+(h_{\text{Körper}}-0.3-z)\cdot (h_{\text{Körper}}-0.3-h_{Schritt})}{{\sqrt {(3.66+{\tfrac {b_{\text{Hüfte}}}{2}}-y)^{2}+(h_{\text{Körper}}-0.3-z)^{2}}}\cdot {\sqrt {({\tfrac {3b_{\text{Hüfte}}}{2}})^{2}+(h_{\text{Körper}}-0.3-h_{Schritt})}}}}}{\text{ω}}}+t_{Reaktion}&{\text{wenn }}y>3.66\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02eae0b904d162f64a030cc09d5f6a6002a2aa1f)
![{\displaystyle t_{Torwart}={\begin{cases}max{\Biggl (}{\tfrac {{\sqrt {(3.66-{\tfrac {b_{\text{Hüfte}}}{2}}-y)^{2}+(h_{\text{Körper}}-0.3-z)^{2}}}-a}{v_{Torwart}}}+t_{Reaktion};{\tfrac {arccos{\tfrac {(3.66-{\tfrac {b_{\text{Hüfte}}}{2}}-y)\cdot (-{\tfrac {3b_{\text{Hüfte}}}{2}})+(h_{\text{Körper}}-0.3-z)\cdot (h_{\text{Körper}}-0.3-h_{Schritt})}{{\sqrt {(3.66-{\tfrac {b_{\text{Hüfte}}}{2}}-y)^{2}+(h_{\text{Körper}}-0.3-z)^{2}}}\cdot {\sqrt {(-{\tfrac {3b_{\text{Hüfte}}}{2}})^{2}+(h_{\text{Körper}}-0.3-h_{Schritt})}}}}}{\text{ω}}}+t_{Reaktion}{\Biggr )}&{\text{wenn }}y\leq 3.66\\[3pt]max{\Biggl (}{\tfrac {{\sqrt {(3.66+{\tfrac {b_{\text{Hüfte}}}{2}}-y)^{2}+(h_{\text{Körper}}-0.3-z)^{2}}}-a}{v_{Torwart}}}+t_{Reaktion};{\tfrac {arccos{\tfrac {(3.66+{\tfrac {b_{\text{Hüfte}}}{2}}-y)\cdot ({\tfrac {3b_{\text{Hüfte}}}{2}})+(h_{\text{Körper}}-0.3-z)\cdot (h_{\text{Körper}}-0.3-h_{Schritt})}{{\sqrt {(3.66+{\tfrac {b_{\text{Hüfte}}}{2}}-y)^{2}+(h_{\text{Körper}}-0.3-z)^{2}}}\cdot {\sqrt {({\tfrac {3b_{\text{Hüfte}}}{2}})^{2}+(h_{\text{Körper}}-0.3-h_{Schritt})}}}}}{\text{ω}}}+t_{Reaktion}{\Biggr )}&{\text{wenn }}y>3.66\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/810f6f99eaf50a1f7dbd7632d37cf812fbb5409e)


![{\displaystyle t_{Torwart}={\begin{cases}max{\Biggl (}{\tfrac {{\sqrt {(3.66-{\tfrac {b_{\text{Hüfte}}}{2}}-y)^{2}+(h_{\text{Körper}}-0.3-z)^{2}}}-a}{v_{Torwart}}}+t_{Reaktion};{\tfrac {arccos{\tfrac {(3.66-{\tfrac {b_{\text{Hüfte}}}{2}}-y)\cdot (-{\tfrac {3b_{\text{Hüfte}}}{2}})+(h_{\text{Körper}}-0.3-z)\cdot (h_{\text{Körper}}-0.3-h_{Schritt})}{{\sqrt {(3.66-{\tfrac {b_{\text{Hüfte}}}{2}}-y)^{2}+(h_{\text{Körper}}-0.3-z)^{2}}}\cdot {\sqrt {(-{\tfrac {3b_{\text{Hüfte}}}{2}})^{2}+(h_{\text{Körper}}-0.3-h_{Schritt})}}}}}{\text{ω}}}+t_{Reaktion}{\Biggr )}&{\text{wenn }}y\leq 3.66\wedge (y-3,66+{\tfrac {b_{\text{Hüfte}}}{2}})^{2}+(z-h_{\text{Körper}}+0,3)^{2}>a\\[3pt]{\tfrac {arccos{\tfrac {(3.66-{\tfrac {b_{\text{Hüfte}}}{2}}-y)\cdot (-{\tfrac {3b_{\text{Hüfte}}}{2}})+(h_{\text{Körper}}-0.3-z)\cdot (h_{\text{Körper}}-0.3-h_{Schritt})}{{\sqrt {(3.66-{\tfrac {b_{\text{Hüfte}}}{2}}-y)^{2}+(h_{\text{Körper}}-0.3-z)^{2}}}\cdot {\sqrt {(-{\tfrac {3b_{\text{Hüfte}}}{2}})^{2}+(h_{\text{Körper}}-0.3-h_{Schritt})}}}}}{\text{ω}}}+t_{Reaktion}&{\text{wenn }}y\leq 3.66\wedge (y-3,66+{\tfrac {b_{\text{Hüfte}}}{2}})^{2}+(z-h_{\text{Körper}}+0,3)^{2}\leq a\\[3pt]{\tfrac {arccos{\tfrac {(3.66+{\tfrac {b_{\text{Hüfte}}}{2}}-y)\cdot ({\tfrac {3b_{\text{Hüfte}}}{2}})+(h_{\text{Körper}}-0.3-z)\cdot (h_{\text{Körper}}-0.3-h_{Schritt})}{{\sqrt {(3.66+{\tfrac {b_{\text{Hüfte}}}{2}}-y)^{2}+(h_{\text{Körper}}-0.3-z)^{2}}}\cdot {\sqrt {({\tfrac {3b_{\text{Hüfte}}}{2}})^{2}+(h_{\text{Körper}}-0.3-h_{Schritt})}}}}}{\text{ω}}}+t_{Reaktion}&{\text{wenn }}y>3.66\wedge (y-3,66-{\tfrac {b_{\text{Hüfte}}}{2}})^{2}+(z-h_{\text{Körper}}+0,3)^{2}\leq a\\[3pt]max{\Biggl (}{\tfrac {{\sqrt {(3.66+{\tfrac {b_{\text{Hüfte}}}{2}}-y)^{2}+(h_{\text{Körper}}-0.3-z)^{2}}}-a}{v_{Torwart}}}+t_{Reaktion};{\tfrac {arccos{\tfrac {(3.66+{\tfrac {b_{\text{Hüfte}}}{2}}-y)\cdot ({\tfrac {3b_{\text{Hüfte}}}{2}})+(h_{\text{Körper}}-0.3-z)\cdot (h_{\text{Körper}}-0.3-h_{Schritt})}{{\sqrt {(3.66+{\tfrac {b_{\text{Hüfte}}}{2}}-y)^{2}+(h_{\text{Körper}}-0.3-z)^{2}}}\cdot {\sqrt {({\tfrac {3b_{\text{Hüfte}}}{2}})^{2}+(h_{\text{Körper}}-0.3-h_{Schritt})}}}}}{\text{ω}}}+t_{Reaktion}{\Biggr )}&{\text{sonst}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7ba2abe53e631cba21e0327889173ca7e51b712)



![{\displaystyle v_{Ball}>{\begin{cases}{\tfrac {\sqrt {11^{2}+(3.66-y)^{2}+z^{2}}}{max{\Bigg (}{\tfrac {{\sqrt {(3.46-y)^{2}+(k-0.3-z)^{2}}}-{\tfrac {k}{2}}+0.2}{v_{Torwart}}}+t_{Reaktion};{\tfrac {arccos{\tfrac {(k-0.3-z)\cdot ({\tfrac {k}{2}}-0.3)}{{\sqrt {(3.46-y)^{2}+(k-0.3-z)^{2}}}\cdot ({\tfrac {k}{2}}-0.3)}}}{\text{ω}}}+t_{Reaktion}{\Bigg )}}}&{\text{wenn }}y\leq 3.66\wedge (y-3,46)^{2}+(z-k+0,3)^{2}>({\tfrac {k}{2}})-0.2\\[3pt]{\tfrac {\sqrt {11^{2}+(3.66-y)^{2}+z^{2}}}{{\tfrac {arccos{\tfrac {(k-0.3-z)\cdot ({\tfrac {k}{2}}-0.3)}{{\sqrt {(3.46-y)^{2}+(k-0.3-z)^{2}}}\cdot ({\tfrac {k}{2}}-0.3)}}}{\text{ω}}}+t_{Reaktion}}}&{\text{wenn }}y\leq 3.66\wedge (y-3.46)^{2}+(z-k+0,3)^{2}\leq ({\tfrac {k}{2}})-0.2\\[3pt]{\tfrac {\sqrt {11^{2}+(3.66-y)^{2}+z^{2}}}{{\tfrac {arccos{\tfrac {(k-0.3-z)^{\cdot }({\tfrac {k}{2}}-0.3)}{{\sqrt {(3.86-y)^{2}+(k-0.3-z)^{2}}}\cdot ({\tfrac {k}{2}}-0.3)}}}{\text{ω}}}+t_{Reaktion}}}&{\text{wenn }}y>3.66\wedge (y-3.86)^{2}+(z-k+0,3)^{2}\leq ({\tfrac {k}{2}})-0.2\\[3pt]{\tfrac {\sqrt {11^{2}+(3.66-y)^{2}+z^{2}}}{max{\Bigg (}{\tfrac {{\sqrt {(3.86-y)^{2}+(k-0.3-z)^{2}}}+{\tfrac {k}{2}}-0.2}{v_{Torwart}}}+t_{Reaktion};{\tfrac {arccos{\tfrac {(k-0.3-z)^{\cdot }({\tfrac {k}{2}}-0.3)}{{\sqrt {(3.86-y)^{2}+(k-0.3-z)^{2}}}\cdot ({\tfrac {k}{2}}-0.3)}}}{\text{ω}}}+t_{Reaktion}{\Bigg )}}}&{\text{sonst}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6b1eb212e38056b21447a8db006c7a5daafcea9)







![{\displaystyle f:[0,7.32]\times [0,2.44]\to \mathbb {R} ,f(y,z)={\begin{cases}{\tfrac {\sqrt {11^{2}+(3.66-y)^{2}+z^{2}}}{max{\Bigg (}{\tfrac {{\sqrt {(3.46-y)^{2}+(k-0.3-z)^{2}}}-{\tfrac {k}{2}}+0.2}{v_{Torwart}}}+t_{Reaktion};{\tfrac {arccos{\tfrac {(k-0.3-z)\cdot ({\tfrac {k}{2}}-0.3)}{{\sqrt {(3.46-y)^{2}+(k-0.3-z)^{2}}}\cdot ({\tfrac {k}{2}}-0.3)}}}{\text{ω}}}+t_{Reaktion}{\Bigg )}}}&{\text{wenn }}y\leq 3.66\wedge (y-3,46)^{2}+(z-k+0,3)^{2}>({\tfrac {k}{2}})-0.2\\[3pt]{\tfrac {\sqrt {11^{2}+(3.66-y)^{2}+z^{2}}}{{\tfrac {arccos{\tfrac {(k-0.3-z)\cdot ({\tfrac {k}{2}}-0.3)}{{\sqrt {(3.46-y)^{2}+(k-0.3-z)^{2}}}\cdot ({\tfrac {k}{2}}-0.3)}}}{\text{ω}}}+t_{Reaktion}}}&{\text{wenn }}y\leq 3.66\wedge (y-3.46)^{2}+(z-k+0,3)^{2}\leq ({\tfrac {k}{2}})-0.2\\[3pt]{\tfrac {\sqrt {11^{2}+(3.66-y)^{2}+z^{2}}}{{\tfrac {arccos{\tfrac {(k-0.3-z)^{\cdot }({\tfrac {k}{2}}-0.3)}{{\sqrt {(3.86-y)^{2}+(k-0.3-z)^{2}}}\cdot ({\tfrac {k}{2}}-0.3)}}}{\text{ω}}}+t_{Reaktion}}}&{\text{wenn }}y>3.66\wedge (y-3,86)^{2}+(z-k+0,3)^{2}\leq ({\tfrac {k}{2}})-0.2\\[3pt]{\tfrac {\sqrt {11^{2}+(3.66-y)^{2}+z^{2}}}{max{\Bigg (}{\tfrac {{\sqrt {(3.86-y)^{2}+(k-0.3-z)^{2}}}+{\tfrac {k}{2}}-0.2}{v_{Torwart}}}+t_{Reaktion};{\tfrac {arccos{\tfrac {(k-0.3-z)^{\cdot }({\tfrac {k}{2}}-0.3)}{{\sqrt {(3.86-y)^{2}+(k-0.3-z)^{2}}}\cdot ({\tfrac {k}{2}}-0.3)}}}{\text{ω}}}+t_{Reaktion}{\Bigg )}}}&{\text{sonst}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c6f564d35449c53722a5c0d008b09c5a26ca49f)














































![{\displaystyle [0,7.32]\times [0,2.44]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38182004dc420ab359900f646e5f13ec4c4e51bf)








