Kurs:Topologische Invertierbarkeitskriterien/P-Regularität über Quasinormen

Einführung

Wenn wir die ${\mathcal {P}}$ -Regularität eines Elementes $z\in A$ für eine lokalbeschränkte topologische Algebra $(A,\|\cdot \|_{A})$ sprechen, suchen wir nach einer lokalbeschränkten Algebraerweiterungen $(B,\|\cdot \|_{B})$ von $(A,\|\cdot \|_{A})$ in der $z\in A$ invertierbar ist. Dabei reicht es nach dem Korrespondenzsatz p-Halbnormen zeigen, dass eine normierte Algebraerweiterung, dass die Algebraerweiterung $(B,\|\cdot \|_{B})$

durch eine $p$ -Norm topologisiert werden kann oder (alternativ)
die Topologe durch eine Quasinorm $\|\cdot \|_{B})$ erzeugt werden kann

Analog zur Vollständigkeit bei Banachalgebren verändert das die Eigenschaft der Vollständigkeit das Vorgehen nicht, denn ist ein aus $z\in A$ in einer lokalbeschränkten Algebra $(B_{0},{\mathcal {T}}_{B_{0}})$ invertierbar, die nicht vollständig ist, dann vervollständig man ggf. die Algebraerweiterung $B_{0}$ zu $B$ .

Zielsetzung

Zielsetzung einer lokalbeschränkten Algebraerweiterung $(B,\|\cdot \|_{B})$ zu einer gegebenen topologischen Algebra $(A,\|\cdot \|_{A})$ mit $z\in A$ ist es, die gegebene lokalbeschränkte Algebraerweiterung so zu vergrößern, dass diese ein inverses Element $z^{-1}:=b\in B$ in der lokalbeschränkten Algebraerweiterung $B$ besitzt. Als topologieerzeugende $p$ -Gaugefunktionale werden hier Quasinormen $\|\cdot \|_{A}$ und $\|\cdot \|_{B}$ verwendet.

Veranschaulichung

Algebraerweiterung $B$ von $A$ ist hier wieder eine Banachalgebra, die ein inverses Element $b=z^{-1}\in B$ zu einem gegebenen $z\in A$ enthält.

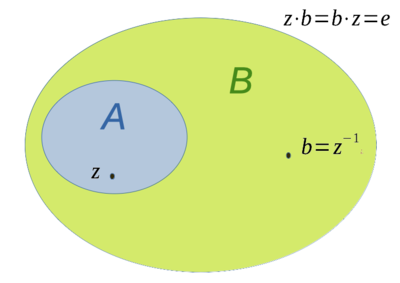
Lokalbeschränkte Algebraerweiterung:

Sei ${\textstyle {\mathcal {P}}_{e}}$ die Klasse der lokalbeschränkten unitalen Algebren und ${\textstyle A\in {\mathcal {P}}_{e}}$ . Die Algebraerweiterung ${\textstyle B\in {\mathcal {P}}_{e}}$ bzw. ${\textstyle {\mathcal {P}}}$ -Erweiterung von ${\textstyle A}$ benötigt nach Definition es einen Algebraisomorphismus ${\textstyle \tau :A\longrightarrow A'\subset B}$ mit:

${\textstyle \tau (e_{_{A}})=e_{_{B}}}$ , wobei ${\textstyle e_{_{A}}}$ ist das Einselement von ${\textstyle A}$ und ${\textstyle e_{_{B}}\in A'}$ das Einselement von ${\textstyle B}$ ist.
${\textstyle A}$ ist homöomorph zu ${\textstyle A'}$ ; d.h. ${\textstyle \tau }$ und ${\textstyle \tau ^{-1}:A'\longrightarrow A}$ sind stetig.

Veranschaulichung - Algebraisomorphismus

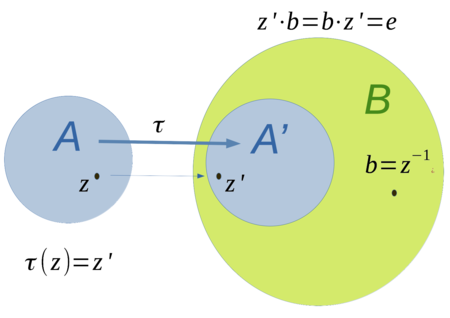
Algebraisomorphismus - Einbettung in die Algebraerweiterung

Im allgemeinen identifiziert man ${\textstyle A}$ mit ${\textstyle A'}$ und schreibt ${\textstyle A\subset B}$ . In der jeweiligen Konstruktion der Algebraerweiterung sieht man, dass die Element aus $x\in A$ mit Elementen $\tau (x)=x+I\in B$ in einem Quotientenraum $B:=A[t]/I$ identifiziert werden.
Sei ${\textstyle {\mathfrak {U}}_{A'}(0)}$ eine Nullumgebungsbasis der Relativtopologie von ${\textstyle B}$ auf ${\textstyle A'}$ und ${\textstyle {\mathfrak {U}}_{A}(0)}$ eine Nullumgebungsbasis von ${\textstyle A}$ , dann kann man die Homöomorphie zwischen ${\textstyle A}$ und ${\textstyle A'}$ wie immer über die Topologie ausdrücken:

{\begin{array}{rcl}\forall _{\displaystyle V\in {\mathfrak {U}}_{A}(0)}\exists _{\displaystyle U\in {\mathfrak {U}}_{A'}(0)}&:&U\subset V\,\,\,(\tau (U)\subset V)\\\forall _{\displaystyle U\in {\mathfrak {U}}_{A'}(0)}\exists _{\displaystyle V\in {\mathfrak {U}}_{A}(0)}&:&V\subset U\,\,\,(\tau ^{-1}(V)\subset U).\end{array}}

Stetigkeit über Quasinormen

Betrachtet man die Quasinormen ${\textstyle \left\|\cdot \right\|_{A'}}$ und ${\textstyle \left\|\cdot \right\|_{A}}$ für Nullumgebungen, so lassen sich die oberen beiden Aussagen wie folgt umformulieren (siehe auch Stetigkeitssatz für lineare Abbildungen):

{\begin{array}{rcl}\exists _{\displaystyle C_{1}>0}\forall _{x\in A}&:&\left\|x\right\|_{A}\leq C_{1}\cdot \left\|\tau (x)\right\|_{A'}\\{\mbox{ bzw. }}&&\left\|\cdot \right\|_{A}\circ \tau \leq C_{1}\cdot \left\|\cdot \right\|_{A'}\\\exists _{\displaystyle C_{2}>0}\forall _{x\in A}&:&\left\|\tau (x)\right\|_{A'}\leq C_{2}\cdot \left\|x\right\|_{A}\\{\mbox{ bzw. }}&&\left\|\cdot \right\|_{A'}\circ \tau \leq C_{2}\cdot \left\|\cdot \right\|_{A}.\end{array}}

Beweisidee 1 - Konstruktion der Algebraerweiterung

Wir betrachten zunächst multiplikative kommuntative Algebren $(A,\|\cdot \|_{A})$ .

Ausgehend von $(A,\|\cdot \|_{A})$ wird die Polynomalgebra $(A[t],\|\!|\cdot |\!\|_{A[t]})$ mit einer Quasinorm $\|\!|\cdot |\!\|_{A[t]}$ topologisiert.
Quasinorm $\|\!|\cdot |\!\|_{A[t]}$ macht $A[t]$ zu einer topologischen Algebra, wobei die Stetigkeit der algebraischen Operationen (insbesondere die Stetigkeit der Cauchy-Multiplikation) nachzuweisen ist.
Übergang zu dem Quotientenraum $B:=A[t]/I$ , wobei das Polynom $o(t):=z\cdot t-e_{A}$ das Hauptideal $I:=o\cdot A[t]$ definiert und $o\in A[t]$ ein Repräsentant des Nullvektors $0_{B}:=I=o+I$ in $B$ ist.
Die Konstruktion des Ideals $I$ liefert die algebraische Invertierbarkeit, denn mit $b(t):=e_{A}\cdot t$ ist $b_{I}:=b+I\in B=A[t]/I$ das inverse Element zu $z\in A$ mit $z_{I}:=\tau (z)=z+I\in B$ mit $z_{I}\cdot b_{I}-e_{B}=0_{B}$ bzw. $z_{I}\cdot b_{I}=e_{B}$ . Die Kommutativität liefert dann, dass auch $b_{I}\cdot z_{I}=e_{B}$ gilt.

Beweisidee

Der Beweis für einen $p$ -normierbaren Raum kann analog zur Banachalgebraerweiterungen der ${\mathcal {B}}$ -Regularität (nach Arens 1958^[1]) geführt werden.

Veranschaulichung Beweisidee

Bei der Konstruktion der Algebraerweiterung, in der ein $z\in A$ invertierbar ist, wird in einem ersten Schritt die Algebra der Polynome $A[t]$ betrachtet. Die folgende Abbildung zeigt, wie die Algebraerweiterung $B$ über die Polynomalgebra konstruiert wird.

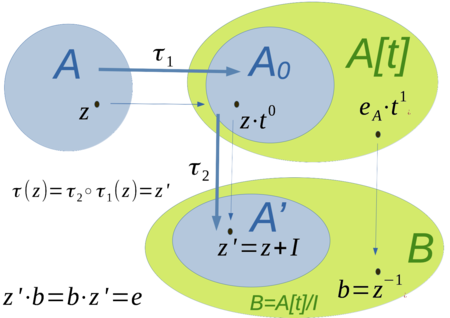
Beweisidee 1 - Konstruktion der Algebraerweiterung

Der Beweis für den Zusammenhang ${\textstyle p}$ -Norm ${\textstyle \left\|\cdot \right\|_{p}}$ und einer Quasihalbnorm ${\textstyle \left\|\cdot \right\|_{Q}}$ findet man bei Köthe (1966)^[2]. Korrespondenzsatz p-Halbnormen spielt später bei der Anwendung auf pseudokonvexe Räume eine wesentliche Rolle.

Beweisidee 2 - Konstruktion der Algebraerweiterung

Ausgehend von $(A,\|\cdot \|_{A})$ wird die Polynomalgebra $(A[t],\|\!|\cdot |\!\|_{A[t]})$ mit einer p-Norm $\|\!|\cdot |\!\|_{A[t]}$ topologisiert und die p-Norm $\|\!|\cdot |\!\|_{A[t]}$ macht $A[t]$ zu einer topologischen Algebra, wobei die Stetigkeit der Cauchy-Multiplikation nachzuweisen ist.
Übergang zu dem Quotientenraum $B:=A[t]/I$ , wobei das Polynom $o(t):=z\cdot t-e_{A}$ das Hauptideal $I:=o\cdot A[t]$ definiert und $o\in A[t]$ ein Repräsentant des Nullvektors $0_{B}:=I=o+I$ in $B$ ist.

Beweisidee 3 - Konstruktion der Algebraerweiterung

Die Konstruktion des Ideals $I$ liefert die algebraische Invertierbarkeit, denn mit $b(t):=e_{A}\cdot t$ ist $b_{I}:=b+I\in B=A[t]/I$ das inverse Element zu $z\in A$ mit $z_{I}:=\tau (z)=z+I\in B$ mit $z_{I}\cdot b_{I}-e_{B}=0_{B}$ bzw. $z_{I}\cdot b_{I}=e_{B}$ . Die Kommutativität liefert dann, dass auch $b_{I}\cdot z_{I}=e_{B}$ gilt.

Normierte Polynomalgebra

Wir betrachten nun zu einer gegeben Banachalgebra ${\textstyle \left(A,\left\|\cdot \right\|_{\mathcal {A}}\right)\in {\mathcal {B}}(\mathbb {K} )}$ die Menge der Polynome mit Koeffizienten in $A$ .

p(t)=\sum _{k=0}^{n}p_{k}\cdot t^{k}{\mbox{ mit }}p_{k}\in A{\mbox{ für }}k\in \{0,1,...,n\}

und Potenzreihen mit Koeffizienten in der Algebra $A$

p(t)=\sum _{k=0}^{\infty }p_{k}\cdot t^{k}{\mbox{ mit }}p_{k}\in A{\mbox{ für }}k\in \mathbb {N} _{o}

Grad von Polynomen

Zunächst einmal würde man Polynome formal eher in der obigen Form mit $n\in \mathbb {N} _{o}$ notieren und mit $p_{n}\not =0_{A}$ würde $n$ den Grad des Polynoms angeben. Für das Cauchyprodukt von zwei Polynomen $p,q\in A[t]$ ist diese Schreibweise allerdings ungeeignet, da bei der Addition und Multiplikation zwei Polynomen $p,q\in A[t]$ die Handhabung des Grades zusätzlichen formalen Aufwand nach sich zieht, der aber für die weitern Betrachtungen von Algebraerweiterungen keine Rolle spielt.

Schreibweise für die Polynomalgebra

Daher werden die Polynome wie folgt über "endliche" Folgen $c_{oo}(A)$ definiert, die ab einer Indexschranke $n\in \mathbb {N} _{o}$ nur noch aus dem Nullvektor $0_{A}$ in $A$ besteht.

p(t)=\sum _{k=0}^{\infty }p_{k}\cdot t^{k}{\mbox{ mit }}(p_{k})_{k\in \mathbb {N} _{0}}\in c_{oo}(A)

Topologischer Nullteiler

Wenn $z\in A$ ein topologischer Nullteiler in $A$ ist (z\in ${\mathcal {TNT}}(A)$ ), gilt:

\displaystyle \inf _{\|x\|_{A}=1}\|z\cdot x\|_{A}=0

Aus der Negation der Eigenschaft erhält man eine Konstante $D>0$ mit:

\displaystyle \|x\|_{A}\leq D\cdot \|z\cdot x\|_{A}

Topologisierung der Polynomalgebra

Die $p\in A[t]$ wird nun mit einer Folge $(C^{k})_{k\in \mathbb {N} }$ mit einer positiven Konstanten $C:=D\cdot K\in \mathbb {R} ^{+}$ topologisiert, wobei ohne Einschränkung $K\geq 1$ die Stetigkeitskonstante der Addition und $D\geq 1$ sich aus der Eigenschaft von $z\in A$ ergibt, kein topologischer Nullteiler zu sein.

\|\!|p|\!\|_{C}:=\displaystyle \sum _{k=0}^{\infty }C^{k}\cdot \|p_{k}\|_{A}{\mbox{ mit }}(p_{k})_{k\in \mathbb {N} _{0}}\in c_{oo}(A)

$c_{oo}(A)$ sind abbrechende Folgen in $A$ , bei denen ab einer Indexschranke nur noch der Nullvektor $0_{A}$ als Folgenglied auftritt.

Homogenität

Die Eigenschaft der Homogenität überträgt sich von Quasinorm $\|\cdot \|_{A}$ auf $\|\!|\cdot |\!\|_{D}$ , denn:

{\begin{array}{rcl}\|\!|\lambda \cdot p|\!\|_{D}&=&\displaystyle \sum _{k=0}^{\infty }C^{k}\cdot \|\lambda \cdot p_{k}\|_{A}\\&=&\displaystyle \sum _{k=0}^{\infty }C^{k}\cdot |\lambda |\cdot \|p_{k}\|_{A}\\&=&\displaystyle |\lambda |\cdot \sum _{k=0}^{\infty }C^{k}\cdot \|p_{k}\|_{A}\,=\,|\lambda |\cdot \|\!|\lambda \cdot p|\!\|_{D}\\\end{array}}

Stetigkeit der Addition

Die Eigenschaft der Stetigkeit der Addition überträgt sich ebenfalls von der Quasinom $\|\cdot \|_{A}$ auf $\|\!|\cdot |\!\|_{D}$ , denn mit $q,r\in A[t]$ :

{\begin{array}{rcl}\|\!|q+r|\!\|_{C}&=&\displaystyle \sum _{k=0}^{\infty }C^{k}\cdot \|q_{k}+r_{k}\|_{A}\\&\leq &\displaystyle \sum _{k=0}^{\infty }C^{k}\cdot K\cdot \left(\|q_{k}\|_{A}+\|r_{k}\|_{A}\right)\\&=&\displaystyle K\cdot \sum _{k=0}^{\infty }\left(C^{k}\cdot \|q_{k}\|_{A}+C^{k}\cdot \|r_{k}\|_{A}\right)\,=\,K\cdot \left(\|\!|q|\!\|_{C}+\|\!|r|\!\|_{C}\right)\\\end{array}}

Die Quasinorm $\|\!|\cdot |\!\|_{C}$ besitzt also die gleiche Stetigkeit

Cauchy-Produkt 1 - Stetigkeit der Multiplikation

Betrachtet man zwei Polynome $q,r\in A[t]$ in dem $p$ -normierten Raum $(A[t],\|\!|\cdot |\!\|_{C})$ .

q(t):=\sum _{k=0}^{\infty }p_{k}\cdot t^{k}{\mbox{ und }}r(t):=\sum _{k=0}^{\infty }q_{k}\cdot t^{k}

Dann liefert die Definition der Norm für das Produkt $p\cdot q$ :

\|\!|q\cdot r|\!\|_{C}=\displaystyle \sum _{n=0}^{\infty }C^{n}\cdot \left\|\sum _{k=0}^{n}q_{k}\cdot r_{n-k}\right\|_{A}

Cauchy-Produkt 2 - Stetigkeit der Multiplikation

Die gegebene $p$ -Norm sei ohne Einschränkung submultiplikativ mit $\|x\cdot y\|_{A}\leq \|x\|_{A}\cdot \|y\|_{A}$

{\begin{array}{rcl}\|\!|q\cdot r|\!\|_{C}&=&\displaystyle \sum _{n=0}^{\infty }C^{n}\cdot \left\|\sum _{k=0}^{n}q_{k}\cdot r_{n-k}\right\|_{A}\leq \displaystyle \sum _{n=0}^{\infty }C^{n}\cdot \sum _{k=0}^{n}\left\|q_{k}\cdot r_{n-k}\right\|_{A}\\&\leq &\displaystyle \sum _{n=0}^{\infty }\sum _{k=0}^{n}C^{n}\cdot \left\|q_{k}\right\|_{A}\cdot \left\|r_{n-k}\right\|_{A}\\&=&\displaystyle \sum _{n=0}^{\infty }\sum _{k=0}^{n}C^{k}\cdot \left\|q_{k}\right\|_{A}\cdot C^{n-k}\cdot \left\|r_{n-k}\right\|_{A}\\&=&\left(\displaystyle \sum _{k=0}^{\infty }C^{k}\cdot \left\|q_{k}\right\|_{A}\right)\cdot \left(\displaystyle \sum _{k=0}^{\infty }C^{k}\cdot \left\|r_{k}\right\|_{A}\right)=\|\!|q|\!\|_{C}\cdot \|\!|r|\!\|_{C}\end{array}}

Topologisierung der Algebraerweiterung

Die Quasinorm auf der Polynomalgebra $(A[t],\|\!|\cdot |\!\|_{C})$ induziert auch die Quasinorm auf dem Quotientenraum $(B,\|\cdot \|_{B})$ mit $B:=A[t]/I$ . Sowohl $(A,\|\cdot \|_{A})$ , $(A[t],\|\!|\cdot |\!\|_{C})$ und $(B,\|\cdot \|_{B})$ sind dann lokalbeschränkte topologische Algebren, wobei die Stetigkeitskonstante der Addition für alle Algebren $K>0$ ist.

Abgeschlossenes Hauptideal in der Polynomalgebra

Für das gegebene $z\in A$ in der kommutativen lokalbeschränkten topologische Algebren $(A,\|\cdot \|_{A})$ definiert man ein Polynom $o\in A[t]$ mit $o(t):=z\cdot t-e_{A}$ , wobei $e_{A}$ das Einselement der Multiplikation in $A$ ist. Als Ideal definiert man $I:={\overline {o\cdot A[t]}}$ als abgeschlossenes Hauptideal in $A[t]$ . Als Untervektorraum $I$ wäre der Quotientenraum auch ein Vektorraum. Die zusätzliche Eigenschaft des Ideals sorgt dafür, dass auch die Multiplikation auf dem Quotientenraum wohldefiniert ist.

Topologisierung des Quotientenraumes Algebraerweiterung

Die Algebraerweiterung wird mit einer Quotientenquasinorm versehen, die wie folgt definiert ist:

\|q_{_{I}}\|_{B}:=\|q+I\|_{B}:=\displaystyle \inf _{r\in I}\|\!|q+r|\!\|_{D}

Dabei bezeichnen man die Nebenklassen in Kurzform mit $q_{I}\in B$ , wobei diese Mengen wie folgt definiert sind:

q_{_{I}}:=q+I:=\{q+r\,:\,r\in I\}

Man muss hier keine Linknebenklassen und Rechtnebenklassen unterscheiden, da die Addition in einem Vektorraum kommuntativ ist.

Stetigkeit Algebrahomomorphismus

Sei $x\in A$ beliebig gewählt, dann gilt mit der Norm $\|\cdot \|_{B}$ auf dem Quotientenraum $B:=A[t]/I$ die folgende Abschätzung

{\begin{array}{rcl}\|\tau (x)\|_{B}&=&\|x_{I}\|_{B}=\|x+I\|_{B}:=\displaystyle \inf _{r\in I}\|\!|x+r|\!\|_{D}\\&\leq &\|\!|x+0_{A[t]}|\!\|_{D}=D^{0}\cdot \|x\|_{A}=\|x\|_{A}\end{array}}

Damit ist $\tau$ stetig (siehe Stetigkeitssatz für lineare Abbildungen).

Struktur der Polynome aus dem Ideal

Betrachten nun das Bild $\tau (A)\subset B$ von $\tau$ in $B$ . Sei nun $A'=\tau (A)=\{x_{I}\,:\,x_{I}=x+I=\tau (x)\}$ gegeben und man betrachtet die Abschätzung für ein beliebiges $q\in A[t]$ mit $r=o\cdot q\in I$ mit $o(t)=z\cdot t-e_{A}$ . Dabei gilt:

{\begin{array}{rcl}r(t)&=&\displaystyle \sum _{k=0}^{\infty }r_{k}\cdot t^{k}=o(t)\cdot q(t)\\&=&-q_{0}+\sum _{k=1}^{\infty }(z\cdot q_{k-1}-q_{k})\cdot t^{k}\end{array}}

Homöomorphie der Einbettung

Nun ist die Algebraerweiterung $B$ topologisiert und es ist noch nachzuweisen, dass die bijektive Abbildung $\tau$ und $\tau ^{-1}$ als lineare Abbildungen stetig sind (siehe Stetigkeitssatz für lineare Abbildungen)

Stetigkeit der Einbettung von A in B

Für die Stetigkeit der Umkehrabbildung $\tau ^{-1}$ gilt bzgl. dem Nullpolynom $0_{A[t]}\in I$ :

\|x+I\|_{B}:=\displaystyle \inf _{r\in I}\|\!|x+r|\!\|_{C}\leq \|\!|x+0_{A[t]}|\!\|_{C}=C^{0}\cdot \|x\|_{A}=\|x\|_{A}

Insgesamt ist der Algebraisomorphismus der Einbettung von $A$ in $A'\subset B:=A[t]/I$ eine Isometrie mit $\|x+I\|_{B}=\|x\|_{A}$ .

Stetigkeit der Umkehrabbildung der Einbettung 1

Unter Verwendung der Abschätzung $\|x\|_{A}\leq D\cdot \|z\cdot x\|_{A}$ erhält man mit $C^{k}=D^{k}\cdot K^{k}$

{\begin{array}{rcl}\|\!|x+r|\!\|_{D}&=&C^{0}\cdot \|x-q_{0}\|_{A}+\sum _{k=0}^{\infty }C^{k}\cdot \|z\cdot q_{k-1}-q_{k}\|_{A}\\\\&\geq &\|x-q_{0}\|_{A}+\sum _{k=0}^{\infty }D^{k}\cdot K^{k-1}\cdot \|z\cdot q_{k-1}\|_{A}-C^{k}\cdot \|q_{k}\|_{A}\\&\geq &\|x-q_{0}\|_{A}+\sum _{k=0}^{\infty }\underbrace {K^{k-1}\cdot D^{k-1}} _{C^{k-1}}\cdot \|q_{k-1}\|_{A}-C^{k}\cdot \|q_{k}\|\\&\geq &\|x-q_{0}\|_{A}+\|q_{0}\|_{A}\geq \|x\|_{A}\end{array}}

Stetigkeitskonstante bei Subtraktion 2

Wendet man die Stetigkeitskonstante $K>0$ der Addition auf eine Subtraktion an, erhält man:

\|x\|_{A}=\|(x-y)+y\|_{A}\geq K\cdot \|x-y\|_{A}+\|y\|_{A}

Die algebraische Umformung liefert die angewendete Ungleichung in der obigen Ungleichungskette mit:

{\frac {1}{K}}\cdot \|x\|_{A}-\|y\|_{A}\leq \|x-y\|_{A}

Stetigkeit der Umkehrabbildung der Einbettung 3

Durch Infimumbildung über alle Polynome $r\in I$ bleibt die obige Ungleichung erhalten. $\|x+I\|_{B}:=\displaystyle \inf _{r\in I}\|\!|x+r|\!\|_{D}\geq \|x\|_{A}$

Siehe auch

Seiteninformation

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Topologische Invertierbarkeitskriterien' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Topologische%20Invertierbarkeitskriterien/P-Regularit%C3%A4t%20%C3%BCber%20Quasinormen
siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.

↑ Arens R., Inverse producing extensions of normed algebras, Trans. Amer. Math. Soc. 88, (1958), S. 536-548
↑ Gottfried Köthe (1966) Topologische lineare Räume, 15.10, S.162-166.

[1] Arens R., Inverse producing extensions of normed algebras, Trans. Amer. Math. Soc. 88, (1958), S. 536-548

[Koethe-2] Gottfried Köthe (1966) Topologische lineare Räume, 15.10, S.162-166.

[1]

[2]