Wenn wir die  -Regularität eines Elementes
-Regularität eines Elementes  für eine multiplikativ pseudokonvexe topologische Algebra
für eine multiplikativ pseudokonvexe topologische Algebra  sprechen, suchen wir nach einer multiplikativ pseudokonvexen Algebraerweiterungen
sprechen, suchen wir nach einer multiplikativ pseudokonvexen Algebraerweiterungen  von
von  in der
in der  invertierbar ist. Dabei besteht
invertierbar ist. Dabei besteht
 und
und
aus einem System von submultiplikativen p-Halbnormen, die die Topologie auf  bzw.
bzw.  erzeugen.
erzeugen.
Der Beweis der Charakterisierung  -Regularität in kommutativen lokalkonvexen Algebren basiert vollständig auf der Beweisidee von Zelazko von 1971[1] permanent sigulären Elemente von kommutativen
-Regularität in kommutativen lokalkonvexen Algebren basiert vollständig auf der Beweisidee von Zelazko von 1971[1] permanent sigulären Elemente von kommutativen  -Algebren zu charakterisieren. Die Beweisidee unter Verwendung
-Algebren zu charakterisieren. Die Beweisidee unter Verwendung  -Normen ist zwar eine Verallgemeinerung des Begriffs einer submultiplikativen Norm, allerdings verändert sich dabei das Vorgehen für die Charakterisierung bei einem Übergang zu Quotientenalgebren im Vergleich zu multiplikativ pseudokonvexen Räumen nicht und man kann den Beweis von Zelazko aus dem Jahr 1971 auch analog auf
-Normen ist zwar eine Verallgemeinerung des Begriffs einer submultiplikativen Norm, allerdings verändert sich dabei das Vorgehen für die Charakterisierung bei einem Übergang zu Quotientenalgebren im Vergleich zu multiplikativ pseudokonvexen Räumen nicht und man kann den Beweis von Zelazko aus dem Jahr 1971 auch analog auf  -Regularität übertragen.
-Regularität übertragen.
MLC-Regularität als Spezialfall der MPC-Regularität
[Bearbeiten]Der Nachweis der Charakterisierung der  -Regularität ist ein Spezialfall der
-Regularität ist ein Spezialfall der  -Regularität für multplikative pseudokonvexe Räume, wobei die
-Regularität für multplikative pseudokonvexe Räume, wobei die  -Normen mit
-Normen mit  homogen sind und damit die Eigenschaften einer Halbnorm erfüllen. Der hier vorgestellt Beweis erzeugt die Algebraerweiterung direkt ohne direkte Verwendung der Charakterisierung der
homogen sind und damit die Eigenschaften einer Halbnorm erfüllen. Der hier vorgestellt Beweis erzeugt die Algebraerweiterung direkt ohne direkte Verwendung der Charakterisierung der  -Regularität für Quotientenräume
-Regularität für Quotientenräume  (siehe MLC-Regularität).
(siehe MLC-Regularität).
Zielsetzung einer multiplikativ lokalkonvexe Algebraerweiterung  zu einer gegebenen topologischen Algebra
zu einer gegebenen topologischen Algebra  mit
mit  ist es, die gegebene multiplikativ lokalkonvexe Algebraerweiterung so zu vergrößern, dass diese ein inverses Element
ist es, die gegebene multiplikativ lokalkonvexe Algebraerweiterung so zu vergrößern, dass diese ein inverses Element  in der multiplikativ lokalkonvexen Algebraerweiterung
in der multiplikativ lokalkonvexen Algebraerweiterung  besitzt. Als topologieerzeugende
besitzt. Als topologieerzeugende  -Gaugefunktionale werden hier Halbnormensystem
-Gaugefunktionale werden hier Halbnormensystem  und
und  verwendet.
verwendet.
Für kommutative multiplikativ pseudokonvexe Algebren  mit unital positivem System von submultiplikativen
mit unital positivem System von submultiplikativen  -Halbnormen erhält man folgende Charakterisierung:
-Halbnormen erhält man folgende Charakterisierung:

 -singulär
-singulär 
 (multiplikativer topologischer Nullteiler)
(multiplikativer topologischer Nullteiler)
 -regulär
-regulär  für alle
für alle  und ein
und ein  mit
mit  für alle
für alle 
Dabei sind  submultiplikative
submultiplikative  -Halbnormen.
-Halbnormen.
Die entscheidende Idee von Zelazko[1] (1971) für den Beweis war die Algebraerweiterung von  in eine Produktraum von Quotientenalgebren
in eine Produktraum von Quotientenalgebren  , wobei ein Ideal
, wobei ein Ideal  über submultiplikativen Halbnormen erzeugt wird. Diese Grundidee ist identisch für eine submultiplikatives
über submultiplikativen Halbnormen erzeugt wird. Diese Grundidee ist identisch für eine submultiplikatives  -Halbnormensystem für die Charakterisierung der
-Halbnormensystem für die Charakterisierung der  -Regularität.
-Regularität.
Algebraerweiterung von MPC-Quotientenalgebren
[Bearbeiten]
Embettung in Quotientenräume bzgl. der submultiplikativen  -Halbnormen bzw. Quasihalbnormen.
-Halbnormen bzw. Quasihalbnormen.
Dabei ist die Submultiplikativität der  -Halbnorm wesentlich für die Idealeigenschaft, denn mit
-Halbnorm wesentlich für die Idealeigenschaft, denn mit

Analog erhält man  über die Submultiplikativität.
über die Submultiplikativität.
Ebenfalls ist die Dreiecksungleichung der  -Halbnorm wesentlich für die Idealeigenschaft, denn mit
-Halbnorm wesentlich für die Idealeigenschaft, denn mit

Anolog liefert die  -Homogenität der
-Homogenität der  -Halbnorm die letzte noch fehlendeIdealeigenschaft, denn mit
-Halbnorm die letzte noch fehlendeIdealeigenschaft, denn mit

Mit dem Ideal  definiert man die Quotientenalgebra
definiert man die Quotientenalgebra  mit der submultiplikativen
mit der submultiplikativen  -Norm:
-Norm:
![{\displaystyle \|\!|\,[x]_{\alpha }|\!\|_{\alpha }:=\|\!|x+N_{\alpha }|\!\|_{\alpha }:=\displaystyle \inf _{u\in N_{\alpha }}\|x+u\|_{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ea206fadac8ce8ae9c68174ffe29586f525210a)
- Zeigen Sie, dass
![{\displaystyle \|\!|\,[x]_{\alpha }|\!\|_{\alpha }=\|x\|_{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01a7786463dbd80c3b393ee977f9fa61ac4e4e53) für alle
für alle  gilt!
gilt!
- Zeigen Sie, dass das
 eine
eine  -Norm auf
-Norm auf  ist, indem Sie die 3 Eigenschaften einer
ist, indem Sie die 3 Eigenschaften einer  -Norm entweder direkt nachweisen oder die Eigenschaft aus ersten Teilaufgabe verwenden.
-Norm entweder direkt nachweisen oder die Eigenschaft aus ersten Teilaufgabe verwenden.
Charakterisierung der MPC-Singularität
[Bearbeiten]Für kommutative multiplikativ pseudokonvexe Algebren  mit einem unital positiven Halbnormensystem erhält man folgende Charakterisierung:
mit einem unital positiven Halbnormensystem erhält man folgende Charakterisierung:
 permanent singulär
permanent singulär  es gibt ein
es gibt ein  mit
mit ![{\displaystyle [z]_{\alpha }\in {\mathcal {TNT}}(A_{\alpha })}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c979b76a5537ee8c76c2707c8e63ecbd29d0948a) also
also ![{\displaystyle [z]_{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/014d3240791fa5f2f40fdd69b8df42628b99a4e6) zumindest in einer Quotientenalgebra
zumindest in einer Quotientenalgebra  ein topologischer Nullteiler ist.
ein topologischer Nullteiler ist. permanent singulär
permanent singulär 
Für kommutative multiplikativ pseudokonvexe Algebren  mit einem unital positiven Halbnormensystem erhält man folgende Charakterisierung:
mit einem unital positiven Halbnormensystem erhält man folgende Charakterisierung:
- Ein Element
 ist
ist  -regulär, wenn für alle
-regulär, wenn für alle  die Äquivalenzklasse
die Äquivalenzklasse ![{\displaystyle [z]_{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/014d3240791fa5f2f40fdd69b8df42628b99a4e6) kein topologischer Nullteiler ist.
kein topologischer Nullteiler ist.

 -regulär
-regulär 
Submultiplikative p-Halbnorm bzw. Quasihalbnorm
[Bearbeiten]Bei den oben genannten Charakterisierungen ist  eine submultiplikative
eine submultiplikative  -Norm bzw. eine submulitplikative Quasinorm.
-Norm bzw. eine submulitplikative Quasinorm.
Algebraerweiterung  von
von  ist hier eine mulitplikative lokalkonvexe Algebra, die ein inverses Element
ist hier eine mulitplikative lokalkonvexe Algebra, die ein inverses Element  zu einem gegebenen
zu einem gegebenen  enthält.
enthält.
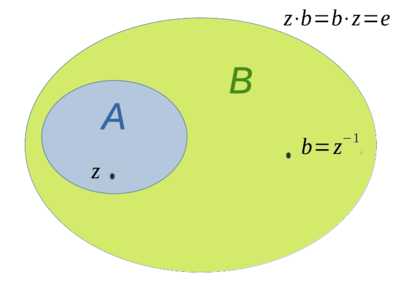
Multiplikative pseudokonvexe Algebraerweiterung
[Bearbeiten]Sei  die Klasse der multiplikativ pseudokonvex unitalen Algebren und
die Klasse der multiplikativ pseudokonvex unitalen Algebren und  . Die Algebraerweiterung
. Die Algebraerweiterung  bzw.
bzw.  -Erweiterung von
-Erweiterung von  benötigt nach Definition es einen Algebraisomorphismus
benötigt nach Definition es einen Algebraisomorphismus
 mit:
mit:
 , wobei
, wobei  ist das Einselement von
ist das Einselement von  und
und  das Einselement von
das Einselement von  ist.
ist. ist homöomorph zu
ist homöomorph zu  ; d.h.
; d.h.  und
und  sind stetig.
sind stetig.
Veranschaulichung der Einbettung in die Algebraerweiterung
[Bearbeiten]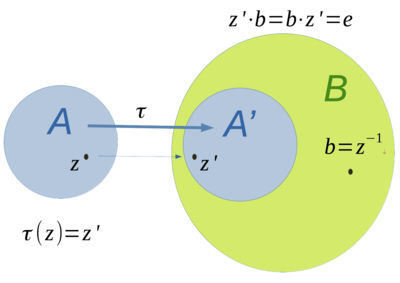
Die Abbildung zeigt, wie die Algebra  in die Algebraerweiterung über
in die Algebraerweiterung über  eingebettet wird.
eingebettet wird.
Algebraisomorphismus - Einbettung in die Algebraerweiterung
[Bearbeiten]- Im allgemeinen identifiziert man
 mit
mit  und schreibt
und schreibt  . In der jeweiligen Konstruktion der Algebraerweiterung sieht man, dass die Element aus
. In der jeweiligen Konstruktion der Algebraerweiterung sieht man, dass die Element aus  mit Elementen
mit Elementen  in einem Quotientenraum
in einem Quotientenraum ![{\displaystyle B:=A[t]/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bc806fa49af6a80a0b8ba7a4eb54a8d503dd8ab) identifiziert werden.
identifiziert werden.
- Sei
 eine Nullumgebungsbasis der Relativtopologie von
eine Nullumgebungsbasis der Relativtopologie von  auf
auf  und
und  eine Nullumgebungsbasis von
eine Nullumgebungsbasis von  , dann kann man die Homöomorphie zwischen
, dann kann man die Homöomorphie zwischen  und
und  wie immer über die Topologie ausdrücken:
wie immer über die Topologie ausdrücken:

Betrachtet man die Halbnormen  und
und  für Nullumgebungen, so lassen sich die oberen beiden Aussagen wie folgt umformulieren (siehe auch Stetigkeitssatz für lineare Abbildungen):
für Nullumgebungen, so lassen sich die oberen beiden Aussagen wie folgt umformulieren (siehe auch Stetigkeitssatz für lineare Abbildungen):

Analogie zu Vorgehen bei der Charakterisierung P-regulärer Elemente
[Bearbeiten]Wir betrachten zunächst multiplikativ lokalkonvexe kommuntative Algebren  und nutzen das Vorgehen bei der Charakterisierung
und nutzen das Vorgehen bei der Charakterisierung  -Regularität für die
-Regularität für die  -Erweiterung von
-Erweiterung von  . Für
. Für  erhalten wir damit auch die Charakterisierung der
erhalten wir damit auch die Charakterisierung der  -Regularität.
-Regularität.
Der Algebrahomomorphismus  bildet nun jedes Element
bildet nun jedes Element  auf die Nebenklasse
auf die Nebenklasse ![{\displaystyle x+I\in B:=A[t]/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed41466c30f79c712ed7afbc89f46eeac9089174) ab. Dabei seien
ab. Dabei seien  kommutative unitale
kommutative unitale  -Algebren über dem Körper
-Algebren über dem Körper  .
.
Abgeschlossenes Hauptideal in der Polynomalgebra
[Bearbeiten]Für das gegebene  in der kommutativen normierten topologische Algebren
in der kommutativen normierten topologische Algebren  definiert man ein Polynom
definiert man ein Polynom ![{\displaystyle o\in A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/084c9c353b0712820bde88d340156c6b728117d2) mit
mit  , wobei
, wobei  das Einselement der Multiplikation in
das Einselement der Multiplikation in  ist. Als Ideal definiert man
ist. Als Ideal definiert man ![{\displaystyle I:={\overline {o\cdot A[t]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1afa070b6145582f7c06f69b2e0616e42b8945d6) als abgeschlossenes Hauptideal in
als abgeschlossenes Hauptideal in ![{\displaystyle A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13daf73f25e64310e7e5d67c5aa8dd4f97cb884f) . Als Untervektorraum
. Als Untervektorraum  wäre der Quotientenraum auch ein Vektorraum. Die zusätzliche Eigenschaft des Ideals sorgt dafür, dass auch die Multiplikation auf dem Quotientenraum wohldefiniert ist.
wäre der Quotientenraum auch ein Vektorraum. Die zusätzliche Eigenschaft des Ideals sorgt dafür, dass auch die Multiplikation auf dem Quotientenraum wohldefiniert ist.
Die Topologie auf ![{\displaystyle A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13daf73f25e64310e7e5d67c5aa8dd4f97cb884f) wird über die folgende submultiplikative
wird über die folgende submultiplikative  -Halbnormen mit
-Halbnormen mit  erzeugt:
erzeugt:

Betrachten Sie eine kommutative Algebra  über dem Körper
über dem Körper  .
.
- Zeigen Sie, dass mit der Abbildung
 und
und  eine Algebraerweiterung von
eine Algebraerweiterung von  nach
nach  definiert wurde!
definiert wurde!
- Zeigen Sie, dass mit der Abbildung
![{\displaystyle \tau _{_{A[t]}}:A\to A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/560e8e559adc8ccd532cca4c7b06359d9fa34cab) und
und ![{\displaystyle \tau _{_{A[t]}}(x)=p_{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d184c2d22dc7f76c2694c6e78c7d0760b77b6e7) mit
mit  eine Algebraerweiterung von
eine Algebraerweiterung von  nach
nach ![{\displaystyle A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13daf73f25e64310e7e5d67c5aa8dd4f97cb884f) definiert wurde!
definiert wurde!
- Begründen Sie, dass das algebraische Vorgehen zu für die Invertierbarkeit mit
 als neutrales Element der Multiplikation in
als neutrales Element der Multiplikation in  sich nicht vom dem Vorgehen in bei der
sich nicht vom dem Vorgehen in bei der  -Regularität bzw.
-Regularität bzw.  -Regularität von kommuntativen Algebren unterscheidet.
-Regularität von kommuntativen Algebren unterscheidet.
- Zeigen Sie, dass
![{\displaystyle A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13daf73f25e64310e7e5d67c5aa8dd4f97cb884f) und auch
und auch ![{\displaystyle B:=A[t]/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bc806fa49af6a80a0b8ba7a4eb54a8d503dd8ab) Hausdorffräume sind!
Hausdorffräume sind!
Topologisierung der Algebraerweiterung
[Bearbeiten]Die Algebraerweiterung wird mit submultiplikative Quotientenhalbnorm mit  versehen, die wie folgt definiert ist:
versehen, die wie folgt definiert ist:

Dabei bezeichnen man die Nebenklassen in Kurzform mit  , wobei diese Mengen wie folgt definiert sind:
, wobei diese Mengen wie folgt definiert sind:

Man muss hier keine Linknebenklassen und Rechtnebenklassen unterscheiden, da die Addition in einem Vektorraum kommuntativ ist.
Sei  beliebig gewählt, dann gilt mit der Norm
beliebig gewählt, dann gilt mit der Norm  auf dem Quotientenraum
auf dem Quotientenraum ![{\displaystyle B:=A[t]/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bc806fa49af6a80a0b8ba7a4eb54a8d503dd8ab) die folgende Abschätzung
die folgende Abschätzung
![{\displaystyle {\begin{array}{rcl}\|\tau (x)\|_{\beta }&=&\|x_{I}\|_{\beta }=\|x+I\|_{\beta }:=\displaystyle \inf _{r\in I}\|\!|x+r|\!\|_{\beta }\\&\leq &\|\!|x+0_{A[t]}|\!\|_{\beta }=D_{\beta }^{0}\cdot \|x\|_{\beta }=\|x\|_{\beta }\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b1e9d3cbfd3d6eda14580102bb18805e69799ea)
Damit ist  stetig (siehe Stetigkeitssatz für lineare Abbildungen).
stetig (siehe Stetigkeitssatz für lineare Abbildungen).
Betrachten nun das Bild  von
von  in
in  .
Sei nun
.
Sei nun  gegeben und man betrachtet die Abschätzung für ein beliebiges
gegeben und man betrachtet die Abschätzung für ein beliebiges ![{\displaystyle q\in A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8d24715a3c26d1fa7abd1b832d7df621423b120) mit
mit  mit
mit  . Dabei gilt:
. Dabei gilt:

Bei der Verwendung der Abschätzung  kann man
kann man  so wählen, dass
so wählen, dass  gilt. Ist das nicht der Fall ersetzt man
gilt. Ist das nicht der Fall ersetzt man  durch eine andere multiplikative Halbnorm
durch eine andere multiplikative Halbnorm  mit:
mit:

und es gilt:

Mit diesem Vorgehen kann man u.a. unital positive Halbnormensysteme auf  generieren in den sowohl
generieren in den sowohl  und damit auch
und damit auch  erfüllt ist.
erfüllt ist.
Man kann also mit dieser Halbnormabschätzung  ein
ein  zuordnen, dass die folgende Bedingung erfüllt:
zuordnen, dass die folgende Bedingung erfüllt:

Damit definiert man einer Abbildung  eine Abbildung, die im Folgenden für die Definition eines submultiplikativen Halbnormensystems auf
eine Abbildung, die im Folgenden für die Definition eines submultiplikativen Halbnormensystems auf ![{\displaystyle A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13daf73f25e64310e7e5d67c5aa8dd4f97cb884f) verwendet wird mit
verwendet wird mit
 .
.
Stetigkeit der Umkehrabbildung der Einbettung
[Bearbeiten]Unter Verwendung der Abschätzung  erhält man mit
erhält man mit 

Bei teleskopierenden Summen werden Summen betrachtet, wobei die Summanden selbst Differenzen sind. Aufeinanderfolgende Teilterme heben sich dabei auf. In der obigen Abschätzung bilden die Terme

eine Telekopsumme.
Durch Infimumbildung über alle Polynome  bleibt die obige Ungleichung erhalten und man erhält die Stetigkeit von
bleibt die obige Ungleichung erhalten und man erhält die Stetigkeit von  .
.

Für die Stetigkeit der Abbildung  gibt es für alle
gibt es für alle  ein
ein  und setzt das Nullpolynom
und setzt das Nullpolynom ![{\displaystyle 0_{A[t]}\in I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fdd47917438e866da00ed13565bd6b943ed260bf) ein:
ein:
![{\displaystyle \|x+I\|_{\beta }:=\displaystyle \inf _{r\in I}\|\!|x+r|\!\|_{\beta }\leq \|\!|x+0_{A[t]}|\!\|_{\beta }=D_{\beta }^{0}\cdot \|x\|_{\beta }\geq \|x\|_{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51f9f8136884bfdeaa57310c3cce3dfc7929f442)
Insgesamt ist der Algebraisomorphismus der Einbettung von  in
in ![{\displaystyle A'\subset B:=A[t]/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2fb696240153ac092adf7e0bc8cebe25afcbd44) eine Hömöomorphismus mit
eine Hömöomorphismus mit  bzw.
bzw.  .
.
Betrachtet man die submultiplikativen Halbnormen  und
und  auf
auf  für Nullumgebungen, so kann man nun die Konstanten analog zum Stetigkeitssatz für lineare Abbildungen wie folgt mit
für Nullumgebungen, so kann man nun die Konstanten analog zum Stetigkeitssatz für lineare Abbildungen wie folgt mit  angeben:
angeben:

Aufgabe - Algebraisomorphismus und Äquivalenz von Gaugefunktionalsystemen
[Bearbeiten]In den obigen beiden Abschätzungen wird die Stetigkeit von lineare Abbildung bzw. von Algebrahomomorphismen verwendet, um die Stetigkeit von  und
und  über Gaugefunktionale auszudrücken. Wir betrachten nun zwei Gaugefunktionalsysteme
über Gaugefunktionale auszudrücken. Wir betrachten nun zwei Gaugefunktionalsysteme  auf
auf  und
und  auf
auf ![{\displaystyle A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13daf73f25e64310e7e5d67c5aa8dd4f97cb884f) und definieren eine weiteres Halbnormensystem
und definieren eine weiteres Halbnormensystem  auf
auf  mit
mit

Dabei wird ![{\displaystyle \tau _{3}(x)=p\in A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8dd153dc14f02525a5145ad2acb65c5dc7299f6) mit
mit  .
Zeigen Sie, dass Gaugefunktionalsysteme
.
Zeigen Sie, dass Gaugefunktionalsysteme  und
und  auf
auf  äquivalente Halbnormensysteme sind (siehe Äquivalenz (Gaugefunktionalsysteme)).
äquivalente Halbnormensysteme sind (siehe Äquivalenz (Gaugefunktionalsysteme)).
Wir betrachten nun zu einer gegebenen (multiplikativ pseudokonvexen)  -Algebra
-Algebra  die Menge der Polynome mit Koeffizienten in
die Menge der Polynome mit Koeffizienten in  .
.

und Potenzreihen mit Koeffizienten in der Algebra 

Auch bei den unächst einmal würde man Polynome formal eher in der obigen Form mit  notieren und mit
notieren und mit  würde
würde  den Grad des Polynoms angeben. Für das Cauchyprodukt von zwei Polynomen
den Grad des Polynoms angeben. Für das Cauchyprodukt von zwei Polynomen ![{\displaystyle p,q\in A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c1a2e0a3e71f7b320f81e4090bb53df3fd3ce9d) ist diese Schreibweise allerdings ungeeignet, da bei der Addition und Multiplikation zwei Polynomen
ist diese Schreibweise allerdings ungeeignet, da bei der Addition und Multiplikation zwei Polynomen ![{\displaystyle p,q\in A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c1a2e0a3e71f7b320f81e4090bb53df3fd3ce9d) die Handhabung des Grades zusätzlichen formalen Aufwand nach sich zieht, der aber für die weitern Betrachtungen von Algebraerweiterungen keine Rolle spielt.
die Handhabung des Grades zusätzlichen formalen Aufwand nach sich zieht, der aber für die weitern Betrachtungen von Algebraerweiterungen keine Rolle spielt.
Daher werden wie bei der P-Regularität die Polynome wie folgt über "endliche" Folgen  definiert, die ab einer Indexschranke
definiert, die ab einer Indexschranke  nur noch aus dem Nullvektor
nur noch aus dem Nullvektor  in
in  besteht.
besteht.

Die ![{\displaystyle p\in A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c749fafdbe6240e74f3f5a2a0b3ad5d59f2ab895) wird nun mit einer Folge
wird nun mit einer Folge  bzgl. einer positiven Konstanten in
bzgl. einer positiven Konstanten in  und einer submultiplikativen Halbnorm
und einer submultiplikativen Halbnorm  topologisiert.
topologisiert.

Betrachtet man zwei Polynome ![{\displaystyle p,q\in A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c1a2e0a3e71f7b320f81e4090bb53df3fd3ce9d) in dem normierten Raum
in dem normierten Raum ![{\displaystyle (A[t],\|\!|\cdot |\!\|_{D})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6bac2275e900239334953d4c6b7e4f9f5491c6cd) .
.

Dann liefert die Definition über  die folgende Halbnorm für das Produkt
die folgende Halbnorm für das Produkt  :
:

Beweisen Sie, dass die folgende Abbildung  eine Norm ist und für alle
eine Norm ist und für alle ![{\displaystyle p,q\in A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c1a2e0a3e71f7b320f81e4090bb53df3fd3ce9d) gilt
gilt

Begründen Sie ferner, dass die Multiplikation auf ![{\displaystyle (A[t],\|\!|\cdot |\!\|_{\widetilde {\mathcal {A}}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d882f375c370777f7c0b1f1ceb403a98e11965bd) stetig ist, wobei man mit der Abbildung
stetig ist, wobei man mit der Abbildung  jedem
jedem  ein
ein  zuordnet, mit
zuordnet, mit  und die Bedingung erfüllt ist, dass:
und die Bedingung erfüllt ist, dass:

Topologisierung der Algebraerweiterung
[Bearbeiten]Die Algebraerweiterung wird mit einer Quotientennorm versehen, die wie folgt definiert ist:

Dabei bezeichnen man die Nebenklassen in Kurzform mit  , wobei diese Mengen wie folgt definiert sind:
, wobei diese Mengen wie folgt definiert sind:

Man muss hier keine Linknebenklassen und Rechtnebenklassen unterscheiden, da die Addition in einem Vektorraum kommuntativ ist.
Zeigen Sie, dass die Polynomalgebra ![{\displaystyle (A[t],\|\!|\cdot |\!\|_{\widetilde {\mathcal {A}}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d882f375c370777f7c0b1f1ceb403a98e11965bd) und
und  Hausdorffräume sind!
Hausdorffräume sind!
- ↑ a b Zelazko Wieslaw, On permanently singular elements in commutative m-convex locally convex algebras, Studia Math. 37 (1971), S. 181-190
Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.
Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Topologische Invertierbarkeitskriterien' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.



































![{\displaystyle \|\!|\,[x]_{\alpha }|\!\|_{\alpha }:=\|\!|x+N_{\alpha }|\!\|_{\alpha }:=\displaystyle \inf _{u\in N_{\alpha }}\|x+u\|_{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ea206fadac8ce8ae9c68174ffe29586f525210a)
![{\displaystyle \|\!|\,[x]_{\alpha }|\!\|_{\alpha }=\|x\|_{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01a7786463dbd80c3b393ee977f9fa61ac4e4e53)

![{\displaystyle [z]_{\alpha }\in {\mathcal {TNT}}(A_{\alpha })}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c979b76a5537ee8c76c2707c8e63ecbd29d0948a)
![{\displaystyle [z]_{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/014d3240791fa5f2f40fdd69b8df42628b99a4e6)





















![{\displaystyle B:=A[t]/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bc806fa49af6a80a0b8ba7a4eb54a8d503dd8ab)









![{\displaystyle x+I\in B:=A[t]/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed41466c30f79c712ed7afbc89f46eeac9089174)



![{\displaystyle o\in A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/084c9c353b0712820bde88d340156c6b728117d2)


![{\displaystyle I:={\overline {o\cdot A[t]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1afa070b6145582f7c06f69b2e0616e42b8945d6)
![{\displaystyle A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13daf73f25e64310e7e5d67c5aa8dd4f97cb884f)




![{\displaystyle \tau _{_{A[t]}}:A\to A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/560e8e559adc8ccd532cca4c7b06359d9fa34cab)
![{\displaystyle \tau _{_{A[t]}}(x)=p_{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d184c2d22dc7f76c2694c6e78c7d0760b77b6e7)







![{\displaystyle {\begin{array}{rcl}\|\tau (x)\|_{\beta }&=&\|x_{I}\|_{\beta }=\|x+I\|_{\beta }:=\displaystyle \inf _{r\in I}\|\!|x+r|\!\|_{\beta }\\&\leq &\|\!|x+0_{A[t]}|\!\|_{\beta }=D_{\beta }^{0}\cdot \|x\|_{\beta }=\|x\|_{\beta }\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b1e9d3cbfd3d6eda14580102bb18805e69799ea)



![{\displaystyle q\in A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8d24715a3c26d1fa7abd1b832d7df621423b120)





















![{\displaystyle 0_{A[t]}\in I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fdd47917438e866da00ed13565bd6b943ed260bf)
![{\displaystyle \|x+I\|_{\beta }:=\displaystyle \inf _{r\in I}\|\!|x+r|\!\|_{\beta }\leq \|\!|x+0_{A[t]}|\!\|_{\beta }=D_{\beta }^{0}\cdot \|x\|_{\beta }\geq \|x\|_{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51f9f8136884bfdeaa57310c3cce3dfc7929f442)
![{\displaystyle A'\subset B:=A[t]/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2fb696240153ac092adf7e0bc8cebe25afcbd44)








![{\displaystyle \tau _{3}(x)=p\in A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8dd153dc14f02525a5145ad2acb65c5dc7299f6)







![{\displaystyle p,q\in A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c1a2e0a3e71f7b320f81e4090bb53df3fd3ce9d)



![{\displaystyle p\in A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c749fafdbe6240e74f3f5a2a0b3ad5d59f2ab895)



![{\displaystyle (A[t],\|\!|\cdot |\!\|_{D})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6bac2275e900239334953d4c6b7e4f9f5491c6cd)






![{\displaystyle (A[t],\|\!|\cdot |\!\|_{\widetilde {\mathcal {A}}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d882f375c370777f7c0b1f1ceb403a98e11965bd)


