Kurs:Lineare Algebra (Osnabrück 2015-2016)/Teil II/Vorlesung 45
- Relationen
Es seien und Mengen. Eine Relation zwischen und ist eine Teilmenge .
D.h. bei einer Relation stehen gewisse Paare in der gegebenen Relation, und die anderen Paare eben nicht. Man schreibt dafür oder oder . Bei spricht man von einer Relation auf . Aus der Analysis sind die Ordnungsrelationen bekannt.
Eine Relation auf einer Menge heißt Ordnungsrelation oder Ordnung, wenn folgende drei Bedingungen erfüllt sind.
- Es ist für alle .
- Aus und folgt stets .
- Aus und folgt .
- Äquivalenzrelationen
Eine Äquivalenzrelation auf einer Menge ist eine Relation , die die folgenden drei Eigenschaften besitzt (für beliebige ).
- Es ist (reflexiv).
- Aus folgt (symmetrisch).
- Aus und folgt (transitiv).
Dabei bedeutet , dass das Paar zu gehört.
Das Urbeispiel für eine Äquivalenzrelation ist die Gleichheit auf einer beliebigen Menge . Unter der Gleichheit ist jedes Element nur mit sich selbst äquivalent.

Häufig interessiert man sich gar nicht so genau für einzelne Objekte, sondern nur für bestimmte Eigenschaften davon. Objekte, die sich bezüglich einer bestimmten, genau definierten Eigenschaft gleich verhalten, kann man dann (bezüglich dieser Eigenschaft) als äquivalent betrachten. Offenbar handelt es sich dabei um eine Äquivalenzrelation. Wenn man sich beispielsweise nur für die Farbe von Objekten interessiert, so sind alle Objekte, die (exakt) gleichfarbig sind, zueinander äquivalent. Wenn man sich bei Tieren nicht für irgendwelche individuellen Eigenschaften interessiert, sondern nur für ihre Art, so sind gleichartige Tiere äquivalent, d.h. zwei Tiere sind genau dann äquivalent, wenn sie zur gleichen Art gehören. Studierende kann man als äquivalent ansehen, wenn sie die gleiche Fächerkombination studieren. Vektoren kann man als äquivalent ansehen, wenn sie zum Nullpunkt den gleichen Abstand besitzen, etc. Eine Äquivalenzrelation ist typischerweise ein bestimmter Blick auf bestimmte Objekte, der unter Bezug auf eine gewisse Eigenschaft gewisse Objekte als gleich ansieht.
Bei den zuletzt genannten „alltäglichen“ Beispielen muss man etwas vorsichtig sein, da im Allgemeinen die Eigenschaften nicht so genau definiert werden. Im Alltag spielt Ähnlichkeit eine wichtigere Rolle als Gleichheit hinsichtlich einer bestimmten Eigenschaft. Die Ähnlichkeit ist aber keine Äquivalenzrelation, da sie zwar reflexiv und symmetrisch ist, aber nicht transitiv. Wenn und zueinander (knapp) ähnlich sind und und ebenso, so kann und schon knapp unähnlich sein (ebenso: lebt in der Nachbarschaft von, ist verwandt mit, etc.).
Die Gleichheit bezüglich einer Eigenschaft wird durch folgende mathematische Konstruktion präzisiert.
Es seien und Mengen und sei eine Abbildung. In einer solchen Situation hat man immer eine Äquivalenzrelation auf dem Definitionsbereich der Abbildung, und zwar erklärt man zwei Elemente als äquivalent, wenn sie unter auf das gleiche Element abgebildet werden, wenn also ist. Wenn die Abbildung injektiv ist, so ist die durch auf definierte Äquivalenzrelation die Gleichheit. Wenn die Abbildung konstant ist, so sind unter der zugehörigen Äquivalenzrelation alle Elemente aus untereinander äquivalent.
Zu einer Abbildung nennt man übrigens die Menge aller Punkte , die auf einen bestimmten Punkt abgebildet werden, die Faser über . Die Äquivalenzklassen (s.u.) sind dann also die Fasern.
Es sei fixiert. Wir betrachten auf die Äquivalenzrelation , bei der zwei Zahlen als äquivalent betrachtet werden, wenn ihre Differenz ein Vielfaches von ist. Zwei Zahlen sind also zueinander äquivalent, wenn man von der einen Zahl zu der anderen durch Sprünge der Sprungweite gelangen kann. Unter Verwendung der Division mit Rest bedeutet dies, dass zwei Zahlen zueinander äquivalent sind, wenn sie bei Division durch den gleichen Rest ergeben.
Wir betrachten die Gaußklammer (oder den „floor“) einer reellen Zahl, also die Abbildung
Eine Zahl wird also auf die größte ganze Zahl abgebildet, die kleiner oder gleich ist (die „Vorkommazahl“). Dabei wird das gesamte ganzzahlige (also mit ganzzahligen Intervallgrenzen) rechtsseitig offene Intervall auf abgebildet. Bezüglich dieser Abbildung sind also zwei reelle Zahlen genau dann äquivalent, wenn sie im gleichen ganzzahligen Intervall liegen.
Statt der Vorkommazahl kann man auch die „Nachkommazahl“ betrachten. Das ist die Abbildung
Unter der durch diese Abbildung definierte Äquivalenzrelation sind zwei reelle Zahlen genau dann gleich, wenn sie die gleiche Nachkommazahl besitzen, und das ist genau dann der Fall, wenn ihre Differenz eine ganze Zahl ist.

Es sei eine Situation gegeben, wo gewisse Orte (oder Objekte) von gewissen anderen Orten aus erreichbar sind oder nicht. Die Erreichbarkeit kann dabei durch die Wahl eines Verkehrsmittels oder durch eine abstraktere (Bewegungs)-Vorschrift festgelegt sein. Solche Erreichbarkeitsrelationen liefern häufig eine Äquivalenzrelation. Dass ein Ort von sich selbst aus erreichbar ist, sichert die Reflexivität. Die Symmetrie der Erreichbarkeit besagt, dass wenn man von nach kommen kann, dass man dann auch von nach kommen kann. Das ist nicht für jede Erreichbarkeit selbstverständlich, für die meisten aber schon. Die Transitivität gilt immer dann, wenn man die Bewegungsvorgänge hintereinander ausführen kann, also zuerst von nach und dann von nach .
Wenn erreichbar beispielsweise dadurch gegeben ist, dass man auf dem Landweg von einem Ort zu einem anderen kommen kann, so sind zwei Ortspunkte genau dann äquivalent, wenn sie auf der gleichen Insel (oder dem gleichen Kontinent) liegen. Inseln und Kontinente sind dann die Äquivalenzklassen.(s.u.) In der Topologie spielt der Begriff des Wegzusammenhangs eine wichtige Rolle: Zwei Punkte sind wegzusammenhängend, wenn man sie durch einen stetigen Weg verbinden kann. Oder: Auf den ganzen Zahlen lebe eine Kolonie von Flöhen, und jeder Flohsprung geht fünf Einheiten weit (in beide Richtungen). Wie viele Flohpopulationen gibt es, welche Flöhe können sich begegnen?
Wir betrachten die Produktmenge , die wir uns als ein Punktgitter vorstellen. Wir fixieren die Sprünge (man denke an Springmäuse, die alle diese Sprünge ausführen können)
und sagen, dass zwei Punkte äquivalent sind, wenn man ausgehend von den Punkt mit einer Folge von solchen Sprüngen erreichen kann. Dies ist eine Äquivalenzrelation (dafür ist entscheidend, dass bei den Sprüngen auch der entgegengesetzte Sprung dazu gehört). Typische Fragestellungen sind: Wie kann man äquivalente Felder charakterisieren, wie entscheiden, ob zwei Felder äquivalent sind oder nicht? Wie viele Äquivalenzklassen gibt es überhaupt, gibt es für sie ein schönes Repräsentantensystem?
Ein Beispiel von dieser Art sind die Läufer beim Schachspiel. Ein Läufer, der auf einem weißen Feld steht, bleibt stets auf einem weißen Feld, und er kann auch jedes weißes Feld erreichen.
- Äquivalenzklassen, Quotientenmenge, kanonische Abbildung
Eine Äquivalenzrelation auf einer Menge kann auch als Zerlegung (Partition) der Menge aufgefasst werden. Hierzu ist der Begriff der Äquivalenzklasse nützlich.
In Worten: ist die Teilmenge aller Elemente von , die zu äquivalent sind. Jedes Element heißt ein Repräsentant für die Äquivalenzklasse , und eine Teilmenge heißt ein Repräsentantensystem für die Äquivalenzrelation, wenn es für jede Klasse genau ein Element aus aus dieser Klasse gibt.
Es sei eine Äquivalenzrelation und die Quotientenmenge. Die Abbildung
heißt kanonische Projektion von .
Es sei eine Menge und eine Äquivalenzrelation auf mit den Äquivalenzklassen und der Quotientenmenge . Dann gelten folgende Aussagen.
- Es ist genau dann, wenn ist, und dies gilt genau dann, wenn .
- ist eine disjunkte Vereinigung.
- Die
kanonische Projektion
ist surjektiv.
- Es ist .
- Es sei eine Abbildung mit für alle mit . Dann gibt es eine eindeutig bestimmte Abbildung mit .
- Es seien und äquivalent und . Dann ist und nach der Transitivität auch , also . Damit stimmen die Äquivalenzklassen überein. Die Implikation von der Mitte nach rechts ist klar, da wegen Äquivalenzklassen nicht leer sind. Es sei nun , und sei ein Element im Durchschnitt. Dann ist und und wegen der Transitivität ist .
- Wegen der Reflexivität ist und daher ist . Wegen Teil (1) ist die Vereinigung disjunkt.
- Die Surjektivität ist klar aufgrund der Definition der Quotientenmenge, und da auf die Klasse geschickt wird.
- Es ist
- Sei gegeben. Die einzige Möglichkeit für ist zu setzen. Es muss aber gezeigt werden, dass diese Abbildung überhaupt wohldefiniert ist, also unabhängig von der Wahl des Repräsentanten ist. Es sei hierzu , also . Dann ist nach der Voraussetzung an aber .
Es sei und . Der ist ein reeller Vektorraum, wobei die Skalarmultiplikation von und mit bezeichnet wird. Es sei weiter
Zwei Punkte werden also als äquivalent erklärt, wenn sie durch Skalarmultiplikation mit einem Skalar ineinander überführt werden können. Ebenso könnte man sagen, dass zwei Punkte als äquivalent gelten, wenn sie dieselbe Gerade durch den Nullpunkt definieren.
Dass wirklich eine Äquivalenzrelation vorliegt, sieht man so. Die Reflexivität folgt aus für jedes . Zur Symmetrie sei , d.h. es gibt ein mit . Dann gilt aber auch , da ja ein Inverses besitzt. Zum Nachweis der Transitivität sei und angenommen, d.h. es gibt mit und . Dann ist insgesamt mit . Die Äquivalenzklassen zu dieser Äquivalenzrelation sind die einzelnen Geraden durch den Nullpunkt (aber ohne den Nullpunkt). Die Quotientenmenge heißt reell-projektiver Raum (der reellen Dimension ) und wird mit bezeichnet.
Es sei die Menge der natürlichen Zahlen und die Produktmenge mit der komponentenweisen Addition. Wir erklären auf eine Relation durch
Dies ist bei genau dann der Fall, wenn es ein (nämlich ) mit
gibt. D.h. die beiden Paare unterscheiden sich um ein Diagonalelement, also um ein Paar, wo beide Komponenten übereinstimmen. Diese Relation ist eine Äquivalenzrelation auf , siehe Aufgabe 45.10. Wenn man als ein quadratisches Gitter anordnet (das ist ein „diskretes Koordinatensystem“), so sind die Äquivalenzklassen durch die Punkte auf einer zur Diagonalen parallelen „diskreten Geraden“ gegeben. Die Punkte mit sind äquivalent zu , sie haben also einen Repräsentanten, bei dem die zweite Komponente ist. Die Punkte mit sind äquivalent zu , sie haben also einen Repräsentanten, bei dem die erste Komponente ist. Die Punkte sind zu äquivalent. Den Repräsentanten einer Äquivalenzklasse, bei dem mindestens eine Komponente ist, nennen wir den Standardvertreter dieser Äquivalenzklasse. Die Standardvertreter sind die diskreten Punkte des begrenzenden Viertelkreuzes; zu einem Punkt ergibt sich der Standardvertreter, wenn man parallel zur Diagonalen in Richtung der Halbachsen wandert, bis man auf einer der Halbachsen landet. Zwei Punkte sind genau dann äquivalent, wenn sie den gleichen Standardvertreter besitzen.
Wir bezeichnen nun die Quotientenmenge, also die Menge der Äquivalenzklassen unter dieser Äquivalenzrelation, als Menge der ganzen Zahlen und bezeichnen sie mit . Jede ganze Zahl hat dann genau einen Standardvertreter der Form mit , der Form oder der Form mit . Eine natürliche Zahl fassen wir von nun an als die ganze Zahl auf.
Wir wollen nun zwei ganze Zahlen, also zwei solche Äquivalenzklassen und miteinander „addieren“, also eine Verknüpfung auf einführen. Der naheliegende Ansatz ist, diese Verknüpfung mittels der komponentenweisen Addition als
zu definieren. Hier tritt das Problem der Wohldefiniertheit auf, denn die Verknüpfung wird erklärt unter Bezug auf Repräsentanten, und es ist nicht von vornherein klar, dass unterschiedliche Repräsentanten zum gleichen Ergebnis führen. Wenn also und sind, so muss man überprüfen, dass
und damit ist. Dies ist der Fall, siehe Aufgabe 45.11. Man kann weiterhin zeigen, dass die so definierte Verknüpfung auf assoziativ und kommutativ ist, dass das neutrale Element der Verknüpfung ist und dass es zu jedem Element ein inverses Element gibt, nämlich .
Wir definieren nun eine Multiplikation auf durch
Dies ist wieder wohldefiniert und man kann zeigen, dass die Multiplikation assoziativ und kommutativ ist mit als neutralem Element und dass das Distributivgesetz gilt.
|
<< | Kurs:Lineare Algebra (Osnabrück 2015-2016)/Teil II | >> |
|---|























































![{\displaystyle {}[x]:={\left\{y\in M\mid (x,y)\in R\right\}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb2893f9a1fd41e58fda3ef2033bdae5213823f1)

![{\displaystyle {}[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c77e93ebf488c686ab4b8693c04bdaae7e8446c)
![{\displaystyle {}y\in [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8fe91cd3cdcac6b78491eccee993a4b7cb6149f)


![{\displaystyle {}M/R:={\left\{[x]\mid x\in M\right\}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4b3a6e37ac167c6a75d7f64b88ea1a6cc24e311)

![{\displaystyle q_{R}\colon M\longrightarrow M/R,\,x\longmapsto [x],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7c96edb2a455ac421608e115251cbbff46ee269)

![{\displaystyle {}[x]=[y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0e31c58238c766c691394b82eb0fc87a5ee0e3f)
![{\displaystyle {}[x]\cap [y]\neq \emptyset }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8deabd43cb75143b1c1b9f06f0e36376615fbc8)
![{\displaystyle {}M=\bigcup _{[x]\in M/\sim }[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9668500885987f8eed93223ae4a06593789272d8)
![{\displaystyle q\colon M\longrightarrow M/\sim ,\,x\longmapsto [x],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93aad292fedc3d5bea8bf5fda10c02c2fc88b15e)
![{\displaystyle {}q^{-1}([x])=[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bb173ce09d3ad591f00a1f6c6c00b0302da17c8)





![{\displaystyle {}u\in [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6a3f679c1338ecdd74dc980755d70d94a834c4d)


![{\displaystyle {}u\in [y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1404b09959e7352fd4601892564498fe1e85d25)
![{\displaystyle {}x\in [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e12337a925c460804120489ba31028dd0fadeff)
![{\displaystyle {}q^{-1}([x])={\left\{y\in M\mid q(y)=[x]\right\}}={\left\{y\in M\mid [y]=[x]\right\}}={\left\{y\in M\mid y\sim x\right\}}=[x]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c95990773ef939c753fe33657ee8f74781384c2)
![{\displaystyle {}[x]\in M/\sim }](https://wikimedia.org/api/rest_v1/media/math/render/svg/09e6ad8b0762f878552d79a7992d41aa87c8949d)

![{\displaystyle {}{\overline {\varphi }}([x]):=\varphi (x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0aeb51915bc1025ad46445ad1264769ddafe76c2)





















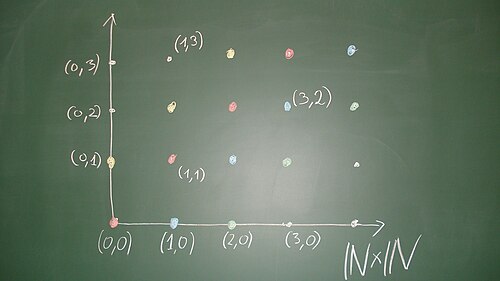




















![{\displaystyle {}[(a,b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad856e5411d0b9ea10ddb04a48932aef19892e7a)
![{\displaystyle {}[(c,d)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b865712c6f9654641f6315839d7fb250d5ed6fa1)

![{\displaystyle {}[(a,b)]\oplus [(c,d)]:=[(a+c,b+d)]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a778629177dd8a896f6ce8cb000f41b321dc395)



![{\displaystyle {}[(a+c,b+d)]=[(a'+c',b'+d')]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b9bc368eabf53b7c89081c97a70ea09b665f4fb)
![{\displaystyle {}[(0,0)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/475a6889495e16a90a7bddd389ad803ee5e078f9)
![{\displaystyle {}[(b,a)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7257885d4524a38fea17a5ad720d33f256cdeaf8)
![{\displaystyle {}[(a,b)]\cdot [(c,d)]:=[(ac+bd,ad+bc)]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e886953fa3c1d350ffa773ec3c5eee3948d2a80c)
![{\displaystyle {}1=[(1,0)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7def7a0131953ef73e591cb841fb440c9b19b53b)