Kurs:Mathematische Modellbildung/Modellierung von Produkteigenschaften
Modellierungsproblem
[Bearbeiten]
Hinführung
[Bearbeiten]Ein wichtiges Objekt im typischen Tagesverlauf eines Schülers oder einer Schülerin ist der Schulranzen. Am Morgen oder am Abend wird er für den Tag gepackt, sodass er in der Schule alle benötigten Gegenstände (Schulsachen) beinhaltet. Dazu zählen z.B. Schulbücher, Schulhefte und Mäppchen, evtl. Taschenrechner, Brotdose, Trinkflasche und vieles mehr. Schaut man sich an Schulen um, sind Schulranzen in den verschiedensten Formen, Farben und Größen zu finden.
Ziel der Modellierung
[Bearbeiten]In diesem Projekt werden praktische Anforderungen an einen Schulranzen gesammelt und daraus optimale Eigenschaften einer solchen Tasche abgeleitet. Ziel ist es, einen Schulranzen zu modellieren, der die gesammelten Anforderungen bestmöglich erfüllt und so größtmögliche Praxistauglichkeit bietet. Anforderungen an einen Schulranzen, die sich aus praktischen Überlegungen ergeben, sind zum Beispiel:
- Er bietet ausreichend Platz, der optimal für alle benötigten Schulsachen genutzt werden kann.
- Er ist regendicht und stabil.
- Er ist leicht und rückenschonend zu tragen.
- Die Herstellung des Ranzens ist kostengünstig und nachhaltig.
In der Modellierung berücksichtigt werden folglich geometrische Eigenschaften ausgewählter Schulsachen, Eigenschaften und Kosten verschiedener Materialien und Überlegungen zur Ergonomie des Rückens, zur Tragfähigkeit eines Kindes und physikalische Aspekte bzgl. der Form des Ranzens. Im Laufe der Modellierungszyklen werden jeweils weitere zusätzliche Anforderungen berücksichtigt.
Zielgruppe der Modellierung
[Bearbeiten]Zielgruppe der Modellierung sind in erster Linie Schüler*innen, da anhand konkreter Anforderungen aus dem Schulalltags ein möglichst praxistauglicher Schulranzen entwickelt werden soll. Die Erkenntnisse dieser Modellierung können im weiteren Verlauf auch in der Produktion von Schulranzen berücksichtigt werden. Daher ist in größerem Kontext auch die Wirtschaft als eine Zielgruppe der Modellierung zu nennen.
Mehrwert der Modellbildung
[Bearbeiten]- Auseinandersetzung mit den relevanten Eigenschaften eines Schulranzens (Erkenntnisgewinn)
- Aufstellen und Abwägen von Kriterien für die Güte eines Schulranzens
- Optimierung des Schulranzens entsprechend der Kriterien (inklusive Prüfung der Kriterien)
- Entwicklung eines möglichst optimalen Schulranzens, der die Kriterien bestmöglich erfüllt
Gruppenmitglieder
[Bearbeiten]- Anthofer, Kim
- Hauck, Nils
- Hohwieler, Laura
- Weis, Marlene
Wiki2Reveal
[Bearbeiten]- Einführung
- Rohdaten
- Grundlagen Sek I
- Theoretische Grundlagen für Zyklus 1
- Modellierungszyklus 1
- Grundlagen Sek II
- Modellierungszyklus 2a
- Modellierungszyklus 2b
- Grundlagen Uni
- Modellierungszyklus 3
- Implementation in Tabellenkalkulation
- Implementation in GeoGebra
- Implementation in wxMaxima
- Implementation in Octave
Zuordnung zu Nachhaltigkeitszielen
[Bearbeiten]
- Das Projekt entwickelt einen möglichst praktischen Schulranzen, der an die Rückenform von Schülerinnen und Schülern angepasst ist. Dabei werden medizinische und physikalische Aspekte berücksichtigt, um ein gesundes Tragen zu ermöglichen und so die Gesundheit der Schülerinnen und Schüler zu fördern.

- SDG 4: Quality Education:Das Projekt entwickelt einen Schulranzen, der den praktischen Anforderungen im Schulalltag gerecht wird und so durch Vorhandensein benötigter Materialien hochwertige Bildung ermöglicht. Durch seinen niedrigen Preis soll er möglichst vielen Familien zugänglich sein und den Zugang zu Bildung auch für einkommensschwächere Familien erleichtern.

- SDG 12: Responsible Consumption and Production:Das Projekt entwickelt einen Schulranzen, der möglichst kostengünstig und nachhaltig produziert wird. Indem praktische Anforderungen erfüllt werden und auf Langlebigkeit geachtet wird, wird einer oberflächlichen Nutzung und verfrühtem Wegwerfen vorgebeugt.
Rohdaten
[Bearbeiten]Schulmaterialien
[Bearbeiten]Vorgehensweise
[Bearbeiten]Als Grundlage für die Modellierung des Schulranzens wurden Informationen über in der Schule benötigte Gegenstände erhoben.
Dies geschah durch eigene Überlegungen und Untersuchungen der Projektgruppe und Befragen von Schüler*innen. Die Ergebnisse sind in den folgenden Abschnitten zusammengefasst.
Schulbücher
[Bearbeiten]Ein wichtiger Teil des Inhalts eines Schulranzens machen Schulbücher, -hefte und Arbeitshefte aus. Um möglichst fundierte Aussagen über die benötigen Bücher und Hefte treffen zu können, wurden hier besonders ausführlich Daten erhoben. Durch selbst durchgeführt Messungen von einigen gängigen Schulbüchern in der Universitäts-Bibliothek Landau wurden Daten gewonnen und in einer Tabelle zusammengetragen. Ergänzt wurde diese Erhebung durch die Ergebnisse der Befragung einiger Schüler*innen der Klassenstufen 7-10, die verschiedene Schulen in Landau und Umgebung besuchen.
Mithilfe der verwendeten Tabellenkalkulation LibreOffice Calc wurden die Mittelwerte über die jeweiligen Maße und das Gewicht der Schulbücher gebildet und so für jedes Schulfach durchschnittliche Werte für Maße und Gewicht ermittelt. Durch diese Vorgehensweise soll berücksichtigt werden, dass an verschiedenen Schulen und in den verschiedenen Klassenstufen jeweils unterschiedliche Schulbücher verwendet werden.
Folgende Tabelle zeigt die auf eine Nachkommastelle gerundeten Mittelwerte:
Hefte und Arbeitshefte Länge in cm Breite in cm Höhe in cm Gewicht in g Schulheft 31,5 21 0,3 80 Arbeitsheft 30 21 0,7 302
Schulbücher und Anzahl Schulhefte pro Fach Länge in cm Breite in cm Höhe in cm Gewicht in g Anzahl Schulhefte Anzahl Arbeitshefte Biologie 26,5 20 1,5 711,0 1 0 Chemie 26,5 19,8 2 917,8 1 0 Deutsch 25,6 20,3 1,8 859,9 1 1 Englisch 26,3 19,5 1,2 568,8 1 1 Erdkunde 26,5 20,4 1,2 593,8 1 0 Französisch 16,4 19,9 1,2 600,1 1 1 Geschichte 26,4 20 1,5 745,4 1 0 Latein 25,2 18,6 2,4 1062,4 1 0 Mathematik 26,5 20,0 1,3 665,8 1 1 Musik 26,3 19,5 1,3 612,7 1 0 Physik 26,6 19,6 2,0 965,2 1 0 Religion 24,8 20,0 1,4 621,8 1 0 Sozialkunde 26,5 19,7 1,8 819,3 1 0
Stundenpläne
[Bearbeiten]Um im Verlauf der Modellierung Aussagen über die benötigten Schulbücher pro Schultag treffen zu können, wurden im zweiten Schritt zwei Stundenpläne einer 8. und einer 10. Klasse verschiedener Schulen betrachtet. Diese sind im Folgenden dargestellt:
Stundenplan 8. Klasse Montag Dienstag Mittwoch Donnerstag Freitag Stunde 1 Englisch Mathe Musik Deutsch Deutsch Stunde 2 Erdkunde Latein Geschichte Latein Deutsch Stunde 3 Mathe Englisch Mathe Sport Latein Stunde 4 Musik Deutsch Mathe Sport Sport Stunde 5 Geschichte Erdkunde Kunst Englisch Chemie Stunde 6 Latein Physik Kunst Chemie Physik
Stundenplan 10. Klasse Montag Dienstag Mittwoch Donnerstag Freitag Stunde 1 Sozialkunde Französisch Geschichte Englisch Mathe Stunde 2 Deutsch Religion Latein Bio Physik Stunde 3 Deutsch Mathe Deutsch Physik Bio Stunde 4 Geschichte Englisch Mathe Religion Erdkunde Stunde 5 Latein Latein Chemie Mathe Kunst Stunde 6 Chemie Englisch Sozialkunde Kunst Stunde 7 Sport Französisch Stunde 8 Sport
Im Kapitel zu Modellierungszyklus 1 wird beschrieben, wie die Stundenpläne in die Modellierung einbezogen wurden.
Weitere Gegenstände
[Bearbeiten]Neben Schulbüchern, -heften und Arbeitsheften benötigen Schüler*innen in der Schule weitere Gegenstände, von denen einige von der Projektgruppe selbst ausgemessen und gewogen wurden. Die Ergebnisse sind in folgender Tabelle zusammengefasst:
Sonstige Gegenstände (quaderförmig) Länge in cm Breite in cm Höhe in cm Gewicht in kg Brotdose* 16 11,5 5,5 310 Mäppchen* 18 7,5 7,5 344 Taschenrechner 16 8,5 1,5 130 Zirkel 22,5 8 2,2 141 Hausaufgabenheft 21 15 0,7 162
Sonstige Gegenstände (zylinderförmig) Durchmesser in cm Höhe in cm Umfang in cm Gewicht in g 1l-Flasche* 8 25,5 25,5 1161 Müsli-Becher 10,5 15,5 33,5 225 Schirm 5 29 18,5 210
*Hinweis: Die Gewichtsangaben von Brotdose, Mäppchen und Flasche beziehen sich jeweils auf die gefüllten Gegenstände.
Bewertung
[Bearbeiten]Es wurde versucht, durch Erhebung möglichst umfangreicher Daten einen realistischen Durchschnittswert für die in der Schule benötigten Gegenstände zu ermitteln. Dies ist aufgrund der unterschiedlicher Schulbücher in verschiedenen Klassenstufen und Schulen erforderlich. Der Tatsache, dass an verschiedenen Wochentagen und in verschiedenen Situationen unterschiedlich viele Hefte und Bücher benötigt werden, kann man jedoch auch mit der Bildung von Mittelwerten nicht gerecht werden. Hinzu kommt, dass in manchen Unterrichtsreihen zeitweise kein Buch benötigt wird oder zwei Schüler*innen gemeinsam ein Buch verwenden können. Auch an einzelnen Tagen kann es Schwankungen geben, z.B. wenn Klassenarbeiten geschrieben werden, Projektarbeiten durchgeführt werden, etc. Ein weiterer Punkt ist, dass an einigen Schulen Schließfächer oder Spinde zur Verfügung stehen und die Schüler*innen alle zuhause nicht benötigten Hefte und Bücher in der Schule lassen können, was wiederum den Inhalt des Schulranzens beeinflusst. Die Berechnung von Mittelwerten stellt daher nur einen groben Richtwert dar, der die Realität aufgrund der genannten Abweichungen in konkreten Situationen nur bedingt abbilden kann. Zudem wird die Berechnung durch Ungenauigkeiten beim Messen und Rundungen im Prozess der Mittelwert-Bestimmung ungenau.
An dieser Stelle wurde die Entscheidung getroffen, den durchschnittlichen Schulranzeninhalt durch Mittelwerte zu bestimmen. Dies hat zur Folge, dass an Tagen, an denen viele Unterrichtsmaterialien benötigt werden, der modellierte Schulranzen evtl. zu klein ist und nicht alle Gegenstände fassen kann. Um dieses Problem zu umgehen, wäre es denkbar, anstelle von Mittelwerten jeweils die maximal benötigten Materialien zu betrachten. Ein auf diese Weise modellierter Schulranzen wäre jedoch voraussichtlich für die meisten Schultage zu groß, weshalb hier die Berechnung der Mittelwerte bevorzugt wurde.
Auch die Gegenstände, die neben Büchern und Heften benötigt werden, variieren von Schüler zu Schüler und von Situation zu Situation. So benötigt man z.B. in Mathematik den Zirkel meist nur zeitweise, nicht jeder Schüler / jede Schülerin nimmt einen Schirm mit in die Schule, es gibt viele verschiedene Mäppchen, die sich in Größe, Form und Gewicht unterscheiden und auch Gegenstände wie Trinkflasche und Brotdose können individuell sehr stark variieren: von Schüler*innen mit mehreren Trinkflaschen und verschiedenen Brotdosen über Schüler*innen mit lediglich einer Brötchentüte vom Bäcker bis hin zu Schüler*innen, die weder Essen noch Trinken mitnehmen, sind in einer Klasse erfahrungsgemäß alle Abstufungen zu finden. Auch hier ist es nicht möglich, ein allgemeingültiges Abbild der Realität zu erstellen.
Dennoch werden im Folgenden die obenstehenden Messdaten und Mittelwerte verwendet, im Bewusstsein, dass es nicht möglich ist, auf diese Weise für alle Gegebenheiten den "perfekten" Schulranzen zu modellieren. In den jeweiligen Abschnitten zu den Modellierungszyklen 1 und 2 finden sich darüber hinaus weitere Angaben zu den betrachteten Gegenständen und getroffenen Annahmen.
Medizinische Daten
[Bearbeiten]Körpergröße eines Jugendlichen
[Bearbeiten]Median der Körpergröße nach dem RKI [4]
| Alter | Mädchen | Jungen |
|---|---|---|
| 12 | 157,22 | 152,22 |
| 13 | 159,53 | 159,13 |
| 14 | 162,74 | 166,93 |
| 15 | 164,58 | 173,12 |
| 16 | 165,39 | 176,66 |
Körpergewicht eines Jugendlichen
[Bearbeiten]Median des Körpergewichts nach dem RKI [5]
| Alter | Mädchen | Jungen |
|---|---|---|
| 12 | 44,87 | 43,25 |
| 13 | 50,02 | 48,81 |
| 14 | 54,01 | 55,51 |
| 15 | 56,80 | 61,69 |
| 16 | 58,53 | 66,30 |
Anatomie des Rückens Jugendlicher
[Bearbeiten]Mittelwerte anthropometrischer Maße
| Alter | Mädchen | Jungen |
|---|---|---|
| 8 - 12 Jahre | 31,9 | 34,1 |
| 13 - 16 Jahre | 37,1 | 39,5 |
Messwerte Rückenform
[Bearbeiten]| Person 1 | Person 2 | Person 3 | Person 4 |
|---|---|---|---|
Zur Erhebung und weiteren Verwendung dieser Daten, siehe Modellierungszyklus 3 - Niveau Uni.
Studie zum Gewicht eines Schulranzens
[Bearbeiten]Sehr geläufig zum idealen Gewicht des Schulranzens ist die 10-Prozent-Regel: Schulranzen sollen nur 10 Prozent des Körpergewichts eines Kindes ausmachen. Eine Studie der Universität des Saarlandes hat diese aber widerlegt und folgende Empfehlungen herausgestellt:[7]
- Schulranzengewichte von 20% des Körpergewichts werden problemlos toleriert
- Ab einer Belastung von 30% des Körpergewichts kommt es zu einer Veränderungen des Gangbildes
- Höhere Belastungen sind kurzfristig möglich, wenn
- Kinder keine Rückenschmerzen haben
- sie über eine gute Fitness verfügen
- und der Schulweg nicht länger als 1 km ist
Mathematische Grundlagen für Zyklus 1
[Bearbeiten]Formeln zu geometrischen Figuren und Körpern
[Bearbeiten]Kreis mit Radius r
Zylinder mit Radius r und Höhe h
Kugel mit Radius r
Rechteck mit den Seitenlängen a und b
Quader mit den Seitenlängen a und b und der Höhe h
Würfel mit der Seitenlänge a
Dreieck mit den Seitenlängen a, b, c und der Höhe ha auf der Seite a
Dreiecksprisma (Grundfläche: Dreieck wie oben, Höhe des Prismas: hp)
Statistik
[Bearbeiten]Mittelwert
( gibt die Anzahl der Elemente an, ist der i-te Wert)

Trigonometrie
[Bearbeiten]In der Trigonometrie werden Beziehungen zwischen Winkeln und Seiten in einem Dreieck betrachtet. Hierdurch können fehlende Seitenlängen bzw. Winkel bestimmt werden unter Zuhilfenahme der Kreisfunktionen (Sinus, Cosinus, etc.).
In einem rechtwinkligen Dreieck (siehe Abb.) gelten die folgenden Beziehungen:
Theoretische Grundlagen für Zyklus 1
[Bearbeiten]Hebel und Drehmoment
Im Folgenden werden physikalische Zusammenhänge beschrieben, die bei der Bewertung der Rucksackmodelle berücksichtigt werden können. Die Informationen stammen aus dem Physik-Lehrbuch von Tipler et al. von 2015, S.296-300 [8].
Ein Hebel ist ein starrer Körper, d.h. ein idealisierter, nicht verformbarer Körper, der sich um einen Drehpunkt bewegt. Wird auf den Hebel eine Kraft ausgeübt, wirkt ein Drehmoment auf den Drehpunkt. Das Drehmoment ist die physikalische Größe, die die Drehwirkung von Kräften auf einen Körper beschreibt. Abhängig von der Länge des Hebels und dem Betrag der Kraft, die auf den Hebel wirkt, verändert sich das Drehmoment.
Beim Drehmoment handelt es sich um den Vektor, der senkrecht auf der Ebene steht, die durch die Vektoren (Radiusvektor) und (Kraftvektor) aufgespannt wird. Entsprechend lautet die Formel: .
Der Betrag des Drehmoments in Nm (Newtonmeter) berechnet sich als Produkt des Hebelarms (Abstand von Drehpunkt zur Kraft) und dem Betrag der Kraft . Der Hebelarm lässt sich über die trigonometrische Beziehung im rechtwinkligen Dreieck mit der Formel berechnen, wobei der Winkel zwischen Radius (Hebel) und Kraft ist. So ergibt sich für die Berechnung des Drehmoments die Formel:
Drehmoment (allgemein)
Hierbei ist zu beachten, dass im Fall bei der Berechnung des Hebelarms eigentlich der Nebenwinkel verwendet wird. Aufgrund der Symmetrie der Sinus-Funktion gilt jedoch und damit , weshalb die obenstehende Formel ohne Beachtung der Größe von verwendet werden kann [9].
In der Modellierung des Schulranzens stellt der Boden des Schulranzens den Hebel dar. Je weiter der Rucksack vom Rücken absteht, desto größer ist der Radius . Bei der Kraft, die auf den Hebel wirkt, handelt es sich um die Gewichtskraft , die durch die Masse des Körpers (Schulranzen) und die Erdbeschleunigung erzeugt wird. Sie lässt sich durch die Formel berechnen. Vereinfachend wird angenommen, dass die Gewichtskraft stets senkrecht auf den Boden des Rucksacks wirkt. Mit und ergibt sich zur Berechnung des Drehmoments in diesem Fall die Formel .
Skizze: Schulranzen mit angreifender Kraft (Seitenansicht)
Um die Positionierung der Gegenstände im Rucksack in die Berechnung einfließen zu lassen, ist es sinnvoll, den Rucksack in verschiedene Abschnitte zu unterteilen und so einzelne Teil-Drehmomente zu berechnen, die sich dann zum Gesamt-Drehmoment aufsummieren. Es ergibt sich für Abschnitte folgende Formel zur Berechnung des Drehmoments:
Da die einzelnen Massen der Gegenstände im Rucksack mit dem jeweiligen Radius multipliziert werden, ist das Drehmoment umso größer, je weiter die größeren Massen vom Rücken (Drehpunkt) entfernt sind.
Modellierungszyklus 1 - Niveau Sekundarstufe I
[Bearbeiten]Ziele
[Bearbeiten]Im ersten Modellierungszyklus werden die in der Schule benötigten Gegenständen mithilfe einfacher geometrischer Formen und Körper modelliert. Der Schulranzen wird durch einen Quader dargestellt. Die wichtigste Anforderung an den Schulranzen ist, dass er alle benötigten Gegenstände beinhalten muss. Hierbei werden ggfs. geschickte und ungeschickte Anordnungen der Gegenstände im Schulranzen identifiziert und verglichen. Darüber hinaus sollen Überlegungen bzgl. des Materials angestellt und Materialkosten berechnet werden. In einem weiteren Schritt wird das Gewicht des Rucksacks betrachtet und es werden physikalische Eigenschaften der Gegenstände im Rucksack untersucht.
Ermittlung der inhaltlichen Anforderungen an den Schulranzen
[Bearbeiten]Mithilfe der Stundenpläne und der Mittelwerte der Messdaten der Schulbücher (zu finden unter Rohdaten) wurde ein Durchschnittswert für die Schulbücher ermittelt. Hierfür wurden die pro Schultag verwendeten Materialien entsprechend der Stundenpläne gemittelt (Länge und Breite) bzw. summiert (Höhe und Gewicht). Aus den Werten für die einzelnen Wochentage wurde wiederum ein Mittelwert berechnet, der einen Durchschnittswert für die Schulbücher über die gesamte Woche darstellt. Aus den auf diese Weise erhaltenen Werten für Klasse 8 und Klasse 10 wurde im letzten Schritt wiederum ein Mittelwert gebildet. Gerundet ergab dies einen Quader mit den Maßen 26 x 20 x 8 (in cm) und einem Gewicht von 3883 g.


Analog wurde ein Mittelwert über die pro Schultag benötigten Schul- und Arbeitshefte gebildet, dieser liegt bei 5 Schulheften und 2 Arbeitsheften. Zur Berechnung der Maße dieser Hefte wurden die Maxima von Länge und Breite und die Summen von Höhe und Gewicht verwendet. Es ergibt sich so ein Quader mit den Maßen (gerundet) 32 x 21 x 3 (in cm) mit einem Gewicht von 1004 g.
Im ersten Modellierungszyklus wurde die Annahme getroffen, dass die Schulbücher, -hefte und Arbeitshefte als ein Quader zusammengefasst werden. Verwendet man die Maxima von Länge und Breite und die Summen von Höhe und Gewicht der beiden bisherigen Quader, erhält man einen großen Quader mit den Maßen 32 x 21 x 11 (in cm) und einem Gewicht von 4887 g. Dieser Quader findet sich in den untenstehenden Abbildungen mit der Bezeichnung "Bücherstapel".
Die weiteren in diesem Zyklus betrachteten Gegenstände sind: Mäppchen, Zirkel, Taschenrechner, Hausaufgabenheft, Brotdose, Flasche, Schirm. Die jeweiligen Messdaten zu diesen Gegenständen finden sich im Kapitel Rohdaten.
Vorgehensweise bei der Modellierung
[Bearbeiten]Mithilfe von GeoGebra wurden die Grundflächen der ausgewählten Gegenstände auf verschiedene Weisen in der Ebene angeordnet, sodass alle Gegenstände nebeneinander positioniert sind. Aus Gründen der Einfachheit wurde darauf verzichtet, die Gegenstände übereinander anzuordnen, d.h. zu stapeln. Bei der Modellierung wurde versucht, eine möglichst kleine Grundfläche zu erhalten.
Die Abmessungen des Schulranzens ergeben sich aus den Maxima von Länge und Breite der Gesamtfläche der benötigten Gegenstände. Verschiedene Anordnungen der Gegenstände in der Ebene führen entsprechend zu unterschiedlichen Abmessungen der Grundfläche des Quaders, der den Rucksack darstellt.
Mithilfe des GeoGebra-Werkzeugs "Zum Prisma extrudieren" kann man aus den vorher erstellten Grundflächen geometrische Körper werden lassen, in diesem Fall Zylinder und Quader, die die Gegenstände darstellen. Die Höhe des Rucksacks entspricht dem Maximum der Höhe der benötigten Gegenstände. In diesem Modellierungszyklus ist der höchste Gegenstand in allen Modellen der Bücherstapel mit einer Höhe von 32 cm, da die anderen Gegenstände alle nebeneinander angeordnet und nicht gestapelt werden.
Modell 1
[Bearbeiten]

Eine erste Anordnung der benötigten Gegenstände ergab für Modell 1 einen Quader mit den Maßen 21 x 24,16 x 32 (in cm). Intuitiv und entsprechend eigener Erfahrungen aus der Schulzeit ist es eine Möglichkeit, die Schulbücher und -hefte direkt am Rücken zu tragen (Modell 1a). Es ist jedoch auch vorstellbar, die Ausrichtung der Gegenstände zu verändern und z.B. die Bücher vom Rücken entfernt (Modell 1b) oder seitlich (Modell 1c) zu positionieren. Es wurde darauf verzichtet, ein viertes Modell analog zu Modell 1c aufzunehmen, bei dem sich der Rücken an der linken Seite des Bücherstapels befindet, da dieses Modell keine wesentlichen Unterschiede zu Modell 1c beinhalten würde. Untenstehende Abbildung zeigt die verschiedenen Möglichkeiten der Ausrichtung des Rucksacks in Bezug auf den Rücken, wobei die tatsächliche Größe des Rückens eines Jugendlichen in dieser Phase der Modellierung noch nicht berücksichtigt wurde.
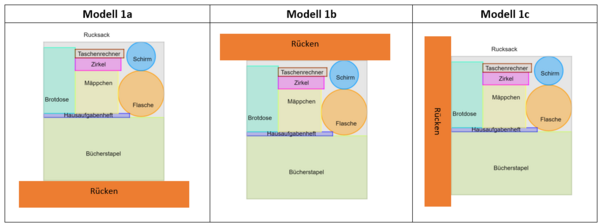
Mithilfe der physikalischen Grundlagen zum Thema Hebel und Drehmoment lassen sich diese drei Modelle vergleichen. Dazu wurden die einzelnen Rucksackmodelle in jeweils drei Abschnitte eingeteilt und die Drehmomente der einzelnen Abschnitte berechnet. Um die Berechnung der Drehmomente zu vereinfachen, wurden die Abschnitte so gewählt, dass sich möglichst viele Gegenstände komplett in einem Abschnitt befinden. An Stellen, an denen dies aufgrund der Anordnung der Gegenstände nicht möglich war, wurden die Drehmomente entsprechend mit anteiliger Masse berechnet. Weiterhin wurde vereinfachend angenommen, dass die Kraft, die durch die Masse eines Rucksack-Abschnitts erzeugt wird, auf einen Punkt wirkt, der sich jeweils am Ende eines solchen Abschnitts befindet. Wichtig ist, dass dies bei allen drei Modellen einheitlich so gemacht wird, um die Vergleichbarkeit der Berechnungen sicherzustellen.
Folgende Übersicht zeigt die Einteilung der Abschnitte der drei Rucksackmodelle und die jeweils zugeordneten Längen der Radiusvektoren , und .

In folgender Tabelle sind die berechneten Drehmomente zusammengefasst:
Drehmoment Modell Drehmoment in Nm 1a 10,190 1b 14,282 1c 10,726
Es ist erkennbar, dass das Drehmoment bei Modell 1b (Bücher am weitesten vom Rücken entfernt) deutlich größer ist als bei den anderen beiden Modellen. Dies lässt sich damit erklären, dass der Bücherstapel der Gegenstand mit der größten Masse ist und durch Multiplikation mit dem Radius, der dem Abstand vom Rücken entspricht, besonders stark in die Berechnung des Drehmoments einfließt. Um den Rücken möglichst wenig zu belasten, ist es daher in der praktischen Umsetzung sinnvoll, die schweren Gegenstände möglichst nah am Rücken zu platzieren und damit das Drehmoment zu minimieren.
Bei obenstehenden Berechnungen wurde nur das Drehmoment berechnet, das sich durch vertikal wirkende Kräfte ergibt. Nicht beachtet wurden seitlich wirkende Kräfte. Es ist jedoch anzunehmen, dass besonders bei Modell 1c (Bücher seitlich positioniert) weitere Kräfte in seitlicher Richtung wirken, da die Massen im Rucksack in horizontaler Richtung nicht gleichmäßig verteilt sind, wodurch eine ungleichmäßige Belastung der Schultern anzunehmen ist.
Bei den folgenden Modellen wird entsprechend dieser Erkenntnisse darauf geachtet, die schwereren Gegenstände möglichst nah am Rücken zu positionieren und, wenn möglich, auf eine gleichmäßige Verteilung der Gegenstände in horizontaler Richtung zu achten.
Modell 2
[Bearbeiten]

Das zweite Modell stellt eine andere Möglichkeit dar, die Gegenstände in der Grundfläche des Schulranzens anzuordnen. Hierbei wurde versucht, die Tiefe des Rucksacks zu minimieren und stattdessen die Gegenstände eher in der Breite anzuordnen. Nebenstehende Abbildung zeigt eine Anordnung der Gegenstände in der Ebene mit den Maßen 27,2 x 19 (in cm). Der Quader, der den Rucksack darstellt, hat entsprechend die Maße 27,2 x 19 x 32 cm. Auch in diesem Modell wurde die Rückengröße noch nicht berücksichtigt, jedoch ist aufgrund eigener Einschätzungen anzunehmen, dass eine Breite von 27,2 cm, wie sie in diesem Modell vorliegt, durchaus realistisch ist bzw. für einen Rucksack keinesfalls zu breit ist.
Da bei diesem Modell bereits berücksichtigt wurde, dass die schweren Gegenstände möglichst nah am Rücken platziert werden sollen, wurde darauf verzichtet, verschiedene Ausrichtungen des Rucksacks zu unterscheiden.
Analog zur Berechnung in Modell 1 wurde auch hier das Drehmoment berechnet. Aufgrund der Anordnung der Gegenstände in der Ebene hat sich hier eine Unterteilung in drei Abschnitte nicht angeboten, weshalb der Rucksack in diesem Modell nur in zwei Abschnitte geteilt wurde.

Drehmoment Modell Drehmoment in Nm 1a 10,190 2 9,529
Die Berechnung des Drehmoments zeigt, dass die in diesem Modell wirkende Kraft geringer ist als im bisher favorisierten Modell 1a. Dies lässt sich damit erklären, dass die Gegenstände mehr in der Breite des Rucksacks angeordnet wurden, wodurch die Länge der Radiusvektoren abnahm, was sich entsprechend auf die Produktbildung bei der Berechnung des Drehmoments auswirkt.
Materialverbrauch und Materialkosten
[Bearbeiten]Die Anforderungen an das Material des Schulranzens sind Regendichte, Stabilität und außerdem angemessene Kosten. Dazu in Frage kommen wird ein Polyesterstoff mit der Kennzeichnung wasserdicht.
Aus Internetseiten einiger Online-Stoffhändler lassen sich folgende Daten sammeln:
| Stoffhändler | Kosten in |
|---|---|
| Stoffe.de [10] | 9,59 |
| Stoff4you [11] | 11,42 |
| Novely [12] | 5,44 |
| Takoy [13] | 4,99 |
| Berotex [14] | 2,57 |
| Pure Textilien [15] | 4,66 |
| Stoffe Hemmers [16] | 9,25 |
| Extrem Textil [17] | 5,78 |
* auf den Webseiten angegeben ist der Preis pro Meter. Dieser wurde mit der jeweils angegebenen Stoffbreite betrachtet und daraus verhältnismäßig der Preis pro berechnet
Beim Berechnen der durchschnittlichen Kosten anhand obiger Daten erhält man nun gerundet einen Preis von 6,71 .
Um den Materialverbrauch herauszufinden, ist es notwendig, die Flächen des bisher noch quaderförmigen Schulranzens zu berechnen. Bekannt sind die vorher herausgefundenen Maße. Diese werden benötigt, um die vier Flächen des Quaders mit der Rechtecks-Flächeninhaltsformel zu berechnen. Außerdem sollte man aus konstruktionstechnischen Gründen mit einer Nahtzugabe von 1cm rechnen, d.h. die Maße der Seitenlängen ändern sich um jeweils 2cm. Folgende Flächeninhalte der einzelnen Rechtecke ergeben sich:

Modell 1:
Maße: 21 x 24,16 x 32 cm
mit Nahtzugabe: 23 x 26,16 x 34 cm
| Rechteck A: | |
| Rechteck B: | |
| Rechteck C: |
Und damit insgesamt (jede Fläche verdoppelt und alles zusammengezählt) die Fläche von oder . Diesen Wert mit den durchschnittlichen Materialkosten multipliziert, ergibt ca. 3,05 € für die gesamten Kosten für den Stoff für einen Rucksack.
Modell 2:
Maße: 27,2 x 19 x 32 cm
mit Nahtzugabe: 29,2 x 21 x 34 cm
| Rechteck A: | |
| Rechteck B: | |
| Rechteck C: |
Und damit insgesamt die Fläche von oder . Diesen Wert mit den durchschnittlichen Materialkosten multipliziert, ergibt ca. 3,11 € für die gesamten Kosten für den Stoff für einen Rucksack.
In diesen Berechnungen ist nicht eingegangen, dass es Mengenrabatte beim Material gibt, von denen man bei einer professionellen Produktion mit großer Stückzahl profitieren würde. Ebenfalls nicht eingegangen sind Kosten für weiteres Material, z.B. Reißverschlüsse, Träger, Polster und die Kosten durch die benötigte Arbeitszeit.
Bewertung und Optimierung
[Bearbeiten]Die Modellierung der Modelle 1 und 2 hat gezeigt, dass es aus physikalischen Gründen sinnvoll ist, die schweren Gegenstände möglichst nah am Rücken zu platzieren und die verfügbare Breite zu nutzen. Offen ist bislang, welchen Einfluss es hat, wenn man die Gegenstände nicht mehr alle in der Ebene positioniert, sondern auch übereinander anordnet. Dies soll im folgenden Modellierungszyklus untersucht werden. Zudem wurde bisher die Rückengröße und -form von Schüler*innen noch nicht berücksichtigt, was ebenso zu einer weiteren Optimierung der Modellierung beitragen kann.
Die vereinfachende Annahme, dass Bücher und Hefte als ein gemeinsamer Quader modelliert werden, soll im folgenden Modellierungszyklus nicht mehr gelten. Stattdessen sollen Bücher und Hefte in zwei getrennten Quadern modelliert werden, um die unterschiedlichen Höhen von Büchern und Heften zu berücksichtigen. Auch die Annahme, dass der Schulranzen als Quader modelliert werden soll, wird im folgenden Modellierungszyklus hinterfragt und stattdessen andere Körper betrachtet. Denkbar ist z.B. das Anbringen von Seitenfächern für Trinkflasche und Schirm oder das Anschrägen der Ober- / Vorderseite des Rucksacks.
Mathemathische Grundlagen für Zyklus 2
[Bearbeiten]Integralrechnung
[Bearbeiten]Mithilfe der Integralrechnung kann der Flächeninhalt zwischen einer Funktion und der x-Achse auf einem festen Intervall berechnet werden. Hierfür wird eine Stammfunktion der gegebenen Funktion benötigt, die durch Integration gebildet wird. Der Flächeninhalt zwischen zwei Funktionen und mit für alle x-Werte im Intervall kann berechnet werden, indem man das Integral der Differenzfunktion oder die Differenz beider Integrale bildet.
Bestimmung Stammfunktion Polynomfunktion
Die Stammfunktion einer Polynomfunktion dritten Grades ist .
Die Stammfunktion einer Parabel (Polynomfunktion zweiten Grades) ist .
Kettenregel für Integrale mit innerer linearer Funktion
Bestimmung Stammfunktion Exponentialfunktion
Für die Stammfunktion einer Exponentialfunktion gilt .
Bestimmung Stammfunktion Sinusfunktion
Die Stammfunktion einer Sinusfunktion ist .
Regressionskurve
[Bearbeiten]Eine Regressionskurve ist ein Hilfsmittel, um einen funktionalen Zusammenhang zwischen mehreren Variablen festzustellen. Ziel ist es, eine Funktion zu finden, die den Zusammenhang zwischen zwei Größen möglichst gut beschreibt. Hierbei kann es sich in der Praxis z.B. um eine Funktion handeln, die gegebene Messpunkte in der Ebene möglichst gut beschreibt. Hiermit lassen sich dann auch weitere Werte schätzen, zu denen keine Daten erhoben wurden.
Ein einfaches Beispiel einer Regressionskurve ist eine Gerade, die Messwerte annähert, wenn ein linearer Zusammenhang zwischen den Werten zu erkennen ist (Lineare Regression). In untenstehendem Modellierungszyklus wurden Regressionskurven sowohl computergestützt als auch von Hand bestimmt. Dazu wurden markante Punkte von Sinus- und Polynomfunktionen identifiziert, anhand derer geeignete Funktionsvorschriften bestimmt wurden.
Bedeutung der Parameter bei der Sinusfunktion
[Bearbeiten]Im Folgenden wird die Sinusfunktion betrachtet und die Auswirkung der einzelnen Parameter beschrieben.
Hierbei seien die Punkte und ein lokales Maximum bzw. lokales Minimum, deren Koordinaten bei der Berechnung bekannt sind. Die x- bzw. y-Koordinaten der beiden Punkte werden als , , und bezeichnet.
Parameter a
Der Parameter gibt die Amplitudenhöhe der Sinusfunktion an. Eine Veränderung des Parameters streckt bzw. staucht die Funktion entlang der y-Achse.
Die y-Koordinaten der Extrempunkte der Standard-Sinusfunktion mit Parameter liegen bei 1 und -1, die Amplitudenhöhe beträgt 1.

Allgemein kann man den Parameter mit folgender Formel berechnen: .

Parameter b
Der Parameter gibt die Periodizität der Sinusfunktion an. Eine Veränderung des Parameters streckt bzw. staucht die Funktion entlang der x-Achse. Die Periodenlänge wird mit bezeichnet.
Die Standard-Sinusfunktion mit hat eine Periodenlänge von .

Die Periodenlänge einer allgemeinen Sinusfunktion ergibt sich zum Beispiel durch , kann aber auch an anderen Stellen berechnet werden, sofern entsprechende Punkte bekannt sind. Der Parameter berechnet sich durch .

Parameter c
Der Parameter gibt die Verschiebung der Funktion entlang der x-Achse an, wobei ein positiver Wert für eine Verschiebung nach rechts verursacht.
Die Standard-Sinusfunktion mit Parameter hat eine Nullstelle bei , die sich in der Mitte zwischen einem Minimum und einem Maximum befindet.

Die Verschiebung der Sinusfunktion in x-Richtung erhält man allgemein zum Beispiel durch , wobei und in diesem Fall aufeinanderfolgende Extrempunkte sein sollten. Wird dies nicht beachtet, ergibt sich evtl. eine um eine halbe Periode verschobene Verschiebung. Aufgrund der Periodizität der Sinusfunktion sind für einen gefundenen Wert für auch alle um verschobenen Werte möglich.

Parameter d
Der Parameter gibt die Verschiebung der Sinusfunktion entlang der y-Achse an, wobei ein positiver Wert für eine Verschiebung nach oben verursacht.
Die Standard-Sinusfunktion mit Parameter hat ihre Wendepunkte stets bei und ihre Extrema bei .

Entsprechend lässt sich die Verschiebung der Sinusfunktion in y-Richtung allgemein mit der Formel berechnen. Auf diese Weise wird die y-Koordinate der Wendepunkte der Sinusfunktion bestimmt (siehe nebenstehende Skizze).

Quadratische Abweichung
[Bearbeiten]Die quadratische Abweichung zwischen Messwerten und zugehörigen Mittelwerten lässt sich mit der folgenden Formel berechnen:
Matrizenschreibweise beim Lösen eines LGS
[Bearbeiten]Eine Möglichkeit, ein lineares Gleichungssystem (LGS) zu lösen, ist, das LGS in die Matrizenschreibweise zu übertragen und mit bekannten Verfahren, z.B. dem Gauß-Algorithmus zu lösen.
Zur Übertragung eines LGS in die Matrixschreibweise werden die Koeffizienten einer Funktion in eine Spalte geschrieben und jede Funktion in eine Zeile. Die Variablen werden in dieser Schreibweise weggelassen, nur die Koeffizienten sind in der Matrix aufgeführt (man spricht daher auch von "Koeffizientenmatrix"). Die Variablen und die Lösung des Gleichungssystems werden jeweils in einem Spaltenvektor zusammengefasst. Das LGS wird so in die Schreibweise überführt.
Eine Koeffizientenmatrix in allgemeiner Form mit 3 Zeilen und 3 Spalten (3x3-Matrix) sieht folgendermaßen aus:
Die Länge des Spaltenvektors muss mit der Spaltenanzahl der Koeffizientenmatrix (hier: 3) übereinstimmen. Die Länge des Spaltenvektors muss mit der Zeilenanzahl der Koeffizientenmatrix (hier: 3) übereinstimmen.
;
Um ein LGS zu lösen, kann man die erweitere Koeffizientenmatrix nutzen. Hierbei handelt es sich um eine vereinfachte Schreibweise, bei der der Vektor , der die rechte Seite des LGS beinhaltet, an die Koeffizientenmatrix angehängt wird.
Die Matrix und der Vektor aus obenstehendem Beispiel werden folgendermaßen zusammengefügt:
Schnitt Ebene - Gerade
[Bearbeiten]Jede Gerade schneidet eine Ebene im Raum, wenn sie nicht parallel zu ihr ist.[18]
Die Gerade in Parameterdarstellung wird in die Ebenengleichung eingesetzt. Man erhält die Gleichung , welche nun nach t aufgelöst werden muss. Setzt man dieses t wieder in die Geradengleichung ein erhält man den Schnittpunkt.
Modellierungszyklus 2 - Niveau Sekundarstufe II
[Bearbeiten]Im zweiten Modellierungszyklus werden die Überlegungen aus Zyklus 1 weitergeführt und in Zyklus 2a dargestellt. Neu hinzu kommt die Betrachtung medizinischer Aspekte, in diesem Fall der Rückenform, die in Zyklus 2b dargestellt werden.
Zyklus 2a - Modellierung des Schulranzens
[Bearbeiten]Ziele
[Bearbeiten]Im zweiten Modellierungszyklus sollen gewinnbringende Erkenntnisse aus dem ersten Zyklus beibehalten und weitergeführt werden. Dazu gehört:
- Schwere Gegenstände werden nah am Rücken platziert.
- Die verfügbare Breite sollte benutzt werden.
Darüber hinaus sollen folgende Aspekte bei der Modellierung betrachtet werden:
- Die Gegenstände können auch übereinander angeordnet (gestapelt) werden.
- Der Bücherstapel (bestehend aus Büchern und Arbeitsheften) wird aufgespalten, Bücher und Hefte / Arbeitshefte werden im Folgenden als zwei getrennte Körper modelliert.
- Der Schulranzen soll an die Rückenbreite und von Jugendlichen angepasst werden.
- Bei der Modellierung des Schulranzens werden verschiedene geometrische Körper in Betracht gezogen und evtl. zusammengesetzt, um den Materialverbrauch zu optimieren.
Ermittlung der inhaltlichen Anforderungen an den Schulranzen
[Bearbeiten]Zur Modellierung des Schulranzens und der Gegenstände, die der Schulranzen fassen soll, wird auf die Ergebnisse aus Modellierungszyklus 1 zurückgegriffen. Da Schulbücher und Hefte / Arbeitshefte getrennt modelliert werden sollen, wird der Bücherstapel in diesem Zyklus ersetzt durch zwei getrennte Quader mit den Maßen
- 26 x 20 x 8 cm (Bücher)
- 32 x 21 x 3 cm (Hefte / Arbeitshefte)
und einem Gewicht von 3883 g (Bücher) und 1004 g (Hefte / Arbeitshefte).
Der Einfachheit halber wird der Quader, der die Hefte und Arbeitshefte darstellt, im Folgenden als "Hefte" bezeichnet.
Vorgehensweise bei der Modellierung
[Bearbeiten]
Grundlage dieser Modellierung ist die Geogebra-Datei des Rucksacks aus dem ersten Zyklus. Zunächst werden die verschiedenen Gegenstände neu angeordnet. Dabei wird das Gewicht, sowie die Größe der Gegenstände in Betracht gezogen. Ganz nah an den Rücken kommen so die Hefte (groß und schwer), danach die Bücher (kleiner und schwerer). Die zwei zylinderförmigen, mit ihrer Form raumverschwenden, Gegenstände (Flasche und Regenschirm) werden außen an die Seiten verfrachtet. Schmale Gegenstände, wie Zirkel und Taschenrechner, werden seitlich in den Rucksack gestellt. Schließlich wird die leichtere Brotdose ganz vorne auf dem Mäppchen gestapelt. Wenn man nun ein Rechteck an diese Anordnung anpasst, erhält man eine kompakte Grundfläche von 23,7 x 18,5 cm für den Rucksack. Diese Breite ist auch damit noch völlig im Rahmen der kleineren möglichen Schulterbreite von 31,9 cm. Dabei nicht in Betracht gezogen ist der Durchmesser von Flasche und Regenschirm in den Seitentaschen von zusammen 13 cm. Wenn man diese dazuzählt, erhält man eine Breite von 36,7 cm. Auch diese ist noch im Rahmen der durchschnittlichen Schulterbreite von 37,24 cm.

Ausgehend davon, dass der Körper, der die Gegenstände umgibt, immernoch ein Quader ist, dessen Form in den nächsten Schritten optimiert werden soll, werden die Ecken der innen stehenden Gegenstände markiert. Aus ihnen werden Geraden konstruiert, die senkrecht zu den seitlichen Quaderseiten des Rucksacks stehen. Die Schnittpunkte der Geraden mit einer dieser Seiten, die als Ebene gedacht werden kann, werden markiert.

Im nächsten Schritt wird eine neue Geogebra-Datei erstellt, bei der die Seitenansicht des Rucksacks im Zweidimensionalen modelliert werden soll. Dabei werden die vorher ermittelten Schnittpunkte mit der Seitenfläche in die zweidimensionale Datei übertragen. Ebenfalls wird die Rechtecksfläche übertragen, von der man bisher ausgeht. Die eingetragenen Punkte lassen eine Abstufung erkennen, bei der klar wird, dass eine waagrechte Gerade als obere Kante nicht sinnvoll ist, da sie viel Platz- und Materialverschwendung verursacht.
Eine Möglichkeit könnte sein, die obere Kante mit einer Parabel auszutauschen. Dazu wird die allgemeine Form der Parabel eingegeben. Nun kann man die Parameter mit dem Schieberegler so einstellen, dass alle Kantenpunkte unterhalb von ihr sind und nicht zu viel Platz verschwendet wird. Dabei erhält man dann die Funktion . Mit dem Integral dieser Funktion, begrenzt auf den Bereich [0,18.5] lässt sich nun die Fläche berechnen und man erhält . Im Vergleich zur Rechteckskante (), bei dessen Integration im selben Bereich man erhält, ist das schon mal eine Verbesserung. Jedoch wäre es sinnvoll, zu überlegen, die überstehende Spitze der Parabel abzuschneiden. Dazu werden die Schnittpunkte der beiden Funktionen berechnet und das Integral der Parabel im Bereich der x-Koordinaten der Punkte. Dieses Integral wird von der vorher berechneten Parabelfläche abgezogen und man erhält .
Das ist schon eine deutliche Verkleinerung der Fläche. Jedoch ist erkennbar, dass immer noch viel Abstand zu den markierten Punkten der Seitenfläche da ist und die Parabel vielleicht nicht die optimalste Form ist. Ähnlich wie bei der Parabel wird nun eine Exponentialfunktion konstruiert. Dazu wird eine allgemeine Funktion mit Parametern eingegeben: . Die Parameter werden wieder mit Schiebereglern angepasst und man erhält . Bei Integration dieser Funktion im Intervall [0,18.5] erhält man für die Fläche , was nochmal eine Verbesserung ist, daher wird im Folgenden von der Exponentialfunktion als Abrundung des Schulranzens ausgegangen.
Modell
[Bearbeiten]Anmerkung: Für die Erstellung des Geogebra Modells des Rucksacks wird eigentlich Mathematik auf Uni-Niveau benötigt. Jedoch wird die Abbildung in Zyklus 2a eingeordnet, da sie zur Illustration des Modells und damit zum Nachvollziehen der vorherigen Schritte dient.
Um den Deckel des Rucksacks nun in GeoGebra zu modellieren, wird die Funktion w(x) mit berechneten Parametern eingegeben und ins Dreidimensionale übertragen . Sie wird in x- und y-Richtung beschränkt mit dem "Wenn"-Befehl, und .
Eine Seitenwand wird durch ein Polygon konstruiert, dessen oberen Punkte auf der Kurve der Kante zum Deckel liegen. Die zweite Seitenwand wird durch Verschieben mit dem Vektor konstruiert.
Analog zur Berechnung in Modellierungszyklus 1 wurde auch hier das Drehmoment berechnet. Aufgrund der Anordnung der Gegenstände in der Ebene hat sich hier eine Unterteilung in vier Abschnitte angeboten, weshalb der Rucksack in diesem Modell nicht in zwei oder drei Abschnitte geteilt wurde.
Folgende Übersicht zeigt die Einteilung der Abschnitte des Rucksackmodells und die jeweils zugeordneten Längen der Radiusvektoren , , und .

| Zyklus | Modell | Drehmoment in Nm |
|---|---|---|
| 1 | 2 | 9,529 |
| 2 | 2a | 5,869 |
Die Berechnung des Drehmoments zeigt, dass die in diesem Modell wirkende Kraft geringer ist als im bisher favorisierten Modell 2 aus dem ersten Zyklus. Dies lässt sich damit erklären, dass die runden Gegenstände, wie Schirm und Trinkflasche, in Seitenfächer des Rucksacks ausgelagert werden. Somit kann der Raum im Quader effektiver genutzt werden. Die Schultasche verliert damit, aber auch mit den übereinander angeordneten Gegenständen an Tiefe. So nimmt die Länge der Radiusvektoren ab, was sich entsprechend auf die Produktbildung bei der Berechnung des Drehmoments auswirkt.
Wie in den vorangegangenen Modellen wird auch in diesem Modell nur die vertikal wirkende Kraft berechnet, während die seitlich einwirkenden Kräfte vernachlässigt werden.
Materialverbrauch und Materialkosten
[Bearbeiten]Schon berechnet ist eine Seitenfläche mit dem Integral der Exponentialfunktion (auf dem Bild Seitenansicht als bezeichnet). Diese wird verdoppelt und man erhält .
Die restlichen zu berechnenden Flächen sind Rechtecksflächen. Rücken, Boden und Vorderteil sind einfach zu berechnen, anhand Koordinaten, die Aussagen über die Maße geben. Dazu noch wichtig zu ermitteln sind die Punkte und , als Anfangs- und Endpunkte von im Intervall [0,18.5]
Rückseite:
Vorderseite:
Unterseite:
Noch zu ermitteln ist die Fläche des Deckels des Rucksacks. Mit dem GG-Befehl "Länge" kann man die Länge der Funktion im Intervall [0,18.5] berechnen. Dabei erhält man einen Wert von 24,53 cm. Da der Deckel eine Rechtecksfläche ist, muss man diesen Wert mit der Breite des Rucksacks multiplizieren:
Deckel:
Alle Flächen zusammengerechnet erhält man: oder . Mit Einbeziehen der Nahtzugabe von 1cm erhält man .
Mit den in Zyklus 1 errechneten durchschnittlichen Materialkosten von ergibt das insgesamt Materialkosten von 2,67 € (vgl. Zyklus 1, Modell 1: 3,05 €)
Bewertung und Optimierung
[Bearbeiten]Die Modellierung des Modells 2a hat gezeigt, dass die Auslagerung von Flasche und Schirm, sowie das Übereinanderstapeln von Mäppchen und Brotdose, unter Berücksichtigung der Rückengröße, sehr platzsparend ist. Durch die Abrundung des Schulranzens mithilfe einer Exponentialfunktion wird weiterer, nicht notwendiger Platz gespart. So verringert sich das Gewicht des Schulranzens und Materialkosten können gespart werden. All das führt dazu, dass sich das Drehmoment im Vergleich zu dem bisher favorisierten Modell aus Zyklus 1 nahezu halbiert und die Last somit besser auf dem Rücken der Schüler*innen verteilt wurde.
Was jedoch nicht in die Berechnung der Kosten eingegangen sind, sind die Außentaschen, die eventuell aus Netzen bestehen würden.
Nicht berücksichtigt wurde bisher die Rückenform von Schüler*innen, was ebenso zu einer weiteren Optimierung der Modellierung beitragen kann. In diesem Zusammenhang bleibt offen, ob die Rückenwand des Schulranzens verändert werden sollte. Drauf wird im zweiten Teil des Modellierungszyklus genauer eingegangen. Zunächst wird die Betrachtung der Rückenform auf das Zweidimensionale beschränkt.
Zyklus 2b - Modellierung medizinischer Aspekte
[Bearbeiten]Ziele
[Bearbeiten]In diesem Kapitel wird die Form eines menschlichen Rückens betrachtet und überlegt, wie ein Rucksack an den Rücken angepasst werden kann. Ziel ist es, die Form des Rückens mithilfe einer Sinus- bzw. Polynomfunktion zweidimensional darzustellen. Im weiteren Verlauf soll der Raum zwischen dem Rücken und der Rückseite des Rucksacks mit Polster ausgefüllt werden, um eine optimale Druckverteilung zu ermöglichen. Die Form und das Volumen dieses Polsters sollen mithilfe der vorherigen Überlegungen bestimmt werden.
Modellierung der Rückenform
[Bearbeiten]Mithilfe nebenstehender Abbildung eines menschlichen Skeletts werden im Folgenden zwei verschiedene Funktionen zur Modellierung der Rückenform hergeleitet. Die Modellierung erfolgt auf zweierlei Wegen: einmal computer-gestützt und einmal von Hand. Die Modellierung von Hand könnte auch im Unterricht durchgeführt werden.

Modellierung einer Sinus-Funktion
[Bearbeiten]Zur computer-gestützten Modellierung der Funktionen mit GeoGebra wurden zwölf Punkte im Intervall [20,75] erstellt, die den Verlauf des Rückens beschreiben.
Mithilfe des Befehls "TrendSin" erhält man zu diesen Punkten eine Regressionskurve der Form . Auf diese Weise ergibt sich aus nebenstehenden Punkten die Funktion .
![Sinusfunktion mit Punkten [19]](http://upload.wikimedia.org/wikipedia/commons/thumb/0/0c/Bild2_Sinus1_mit_Punkten.png/350px-Bild2_Sinus1_mit_Punkten.png)
Bei der händischen Ermittlung der Sinus-Funktion wurde die in der Schule übliche Form gewählt. Man benötigt zur Bestimmung der Parameter die im Intervall [20,75] befindlichen lokalen Extrempunkte und .
Der Parameter a, der die Amplitudenhöhe angibt, berechnet sich durch .
Die Periodenlänge berechnet sich durch . Die Periodizität b erhält man durch .
Zur Ermittlung der Verschiebung in x-Richtung, die der Parameter c angibt, berechnet man die weiteren Extremstellen und . Der Wendepunkt der Sinuskurve liegt in der Mitte zwischen diesen beiden Extremstellen. Diese berechnet sich durch . Entsprechend gilt und damit .
Die Verschiebung in y-Richtung erhält man durch
Auf diese Weise erhält man die Funktion .
![Sinusfunktion von Hand [20]](http://upload.wikimedia.org/wikipedia/commons/thumb/4/49/Bild4_Sinus2_von_Hand.png/300px-Bild4_Sinus2_von_Hand.png)
Modellierung einer Polynomfunktion
[Bearbeiten]Analog zum Befehl "TrendSin" erhält man in GeoGebra mit dem Befehl "TrendPoly" das Regressionspolynom n-ten Grades zu ausgewählten Punkten. Mit n = 3 und den zwölf Punkten entlang des Rückens (siehe Abb.) ergibt sich für die Rückenform die Funktion .
![Polynomfunktion mit Punkten [21]](http://upload.wikimedia.org/wikipedia/commons/thumb/b/be/Bild3_Polynom1_mit_Punkten.png/350px-Bild3_Polynom1_mit_Punkten.png)
Zur händischen Modellierung einer Polynomfunktion dritten Grades der Form werden zusätzlich zu den beiden schon bekannten Extrempunkten und zwei weitere, beliebige Punkte am Rücken gewählt, z.B. die beiden Randpunkte und .
Setzt man die bekannten Wertepaare, die auf der Funktion liegen sollen, in die Funktionsgleichung ein, erhält man folgendes lineare Gleichungssystem in den Parametern :
In eine Matrix übertragen ergibt sich:
Der Lösungsvektor dieses Gleichungssystems ist:
Man erhält die Funktion .
![Polynomfunktion von Hand [22]](http://upload.wikimedia.org/wikipedia/commons/thumb/f/fd/Bild5_Polynomfunktion_von_Hand.png/300px-Bild5_Polynomfunktion_von_Hand.png)
Anmerkung: am Ende des Semesters wurde bemerkt, dass in der Lösung des LGS ein Rechenfehler vorliegt. Der korrekte Lösungsvektor lautet .
In der folgenden Modellierung wird jedoch mit den ursprünglich berechneten Werten weitergearbeitet. Dies müsste in einer weiteren Modellierungsphase korrigiert werden.
Abweichungen
[Bearbeiten]Berechnet man die quadratischen Abweichungen der modellierten Funktionen von den gegebenen Punkten A bis L, ergeben sich folgende Werte (gerundet):
quadratische Abweichungen Funktion Abweichung 1.176 1.188 2.997 6.444
Modellierung des Polsters
[Bearbeiten]Um den Schulranzen möglichst gut an die Rückenform anzupassen, soll der Raum zwischen dem Rücken und der Rückseite des Rucksacks mit einem Polster ausgefüllt werden. Zur Bestimmung von Form und Volumen des Polsters wird angenommen, dass
- die Rückseite des Rucksacks eine gerade Fläche ist, die an der höchsten Stelle des Rückens anliegt und waagrecht zur x-Achse verläuft
- sich die Form des Rückens durch eine zweidimensionale Funktion beschreiben lässt, d.h. dass der Rücken keine Höhenunterschiede in seitlicher Richtung aufweist.
Bei folgenden Berechnungen ist es relevant, dass die Funktionen in GeoGebra in einem realistischen Maßstab bestimmt wurden. Dies wurde anhand eigener Messungen einer beispielhaften Rückenlänge und eines Schulrucksacks und entsprechender Positionierung der Abbildung in GeoGebra sichergestellt und könnte entsprechend für andere Rücken- und Rucksacklängen analog erstellt werden.
Im ersten Schritt werden die Maxima der vier Funktionen im Intervall [20,75] berechnet. Diese stellen die Punkte dar, an denen der Rucksack den Rücken berührt. Die Rückseite des Rucksacks wird entsprechend als konstante Gerade parallel zur x-Achse auf der jeweiligen Höhe modelliert.
Maxima Rückenfunktion y-Koordinate des Maximums Rucksackfunktion 5.0255 5 4.8408 5.627
Durch die Modellierung des Rucksacks als konstante Gerade auf der Höhe des Maximums der jeweiligen Funktion ist sichergestellt, dass eine Rucksackfunktion stets größer oder gleich der zugehörigen Rückenfunktion ist, was im Folgenden bei der Berechnung der Integrale von Bedeutung ist.
Mithilfe von Integralrechnung lässt sich die Fläche zwischen den Rucksackfunktionen und den zugehörigen Rückenfunktionen bestimmen. Diese wird im Folgenden mit bezeichnet. Beispielhaft wird diese Rechnung an zwei Funktionen ansatzweise vorgeführt. Die anderen beiden Integrale lassen sich analog berechnen. Nebenstehende Abbildung zeigt die Funktionen und und das zugehörige Integral .
![Integral der Funktion f1 [23]](http://upload.wikimedia.org/wikipedia/commons/thumb/d/d4/Bild6_Integral_f1.png/400px-Bild6_Integral_f1.png)
Zusammengefasst erhält man folgende Werte für die Fläche zwischen Rucksack und Rücken:
Querschnittsfläche Polster Rückenfunktion Flächeninhalt in 124.15 124.4 115.55 151.1
Mithilfe der unter medizinische Daten erhobenen Daten zur Schulterbreite von Jugendlichen, lässt sich eine durchschnittliche Schulterbreite von für Jugendliche im Altern von 12-16 Jahren berechnen. Hierbei wurde der Unterschied zwischen Jungen und Mädchen nicht berücksichtigt. Verwendet man diese durchschnittliche Schulterbreite als Rucksackbreite und entsprechend als Breite des Polsters, ergeben sich folgende Werte für das Volumen des Polsters bei den unterschiedlichen Funktionen:
Volumen Polster Rückenfunktion Volumen im 4623.346 4632.656 4303.028 5626.964
Bewertung und Optimierung
[Bearbeiten]Der Vergleich der Funktionsvorschriften von und bzw. und zeigt, dass die Vorfaktoren der händisch ausgerechneten Funktionen und denen der von GeoGebra berechneten Funktionen und sehr ähneln. Die unter Abweichungen berechneten Werte für die Abweichung der modellierten Funktionen von den gegebenen Punkten dient als Maß zur Bewertung der modellierten Funktionen. Es zeigt sich, dass die beiden Sinus-Funktionen und weniger Abweichung von den gegebenen Punkten aufweisen und daher für die praktische Umsetzung besser geeignet sind als die Polynomfunktionen und . Die Abweichung der computer-gestützt modellierten Funktion ist dabei nur unwesentlich geringer als die Abweichung der von Hand modellierten Funktion . Dieses Verfahren ist aufgrund des guten Ergebnisses und des relativ geringen Rechenaufwands zu empfehlen. Die Abweichung der von Hand modellierten Polynomfunktion ist mit einem Wert von 6.444 deutlich am größten. Diese Vorgehensweise ist aufgrund der hohen Abweichung und des hohen Rechenaufwands für diese Problemstellung am wenigsten geeignet.
Eine vereinfachende Annahme in diesem Modellierungszyklus war, dass die Form des Rückens nur in vertikaler Richtung mithilfe von Funktionen beschrieben wurde. Unterschiede in horizontaler Richtung wurden hierbei nicht betrachtet. Dies entspricht jedoch nicht der Realität, da z.B. durch die Position der Wirbelsäule und der Rippen auch in horizontaler Richtung Höhenunterschiede am menschlichen Rücken vorliegen. Eine dreidimensionale Modellierung der Rückenform wird in Zyklus 3 vorgenommen.
Außerdem wurde bei der Berechnung des Polstervolumens ein Mittelwert über die Schulterbreite von Jugendlichen zwischen 12 und 16 Jahren gebildet. Hierbei wurden Unterschiede zwischen der Schulterbreite von Mädchen und Jungen nicht beachtet. Diesem Aspekt könnte man in einer getrennten Modellierung von Rucksäcken für Mädchen und Jungen gerecht werden. Weiterhin wurde vernachlässigt, dass Jugendliche in diesem Alter teils stark wachsen und sich entsprechend auch die Schulterbreite verändert. Diese Aspekte gilt es in weiteren Betrachtungen zu berücksichtigen (z.B. durch Modellierung von Rucksäcken mit verstellbaren Rückenhöhen) und entsprechend realitätsgetreuere Modelle zu erstellen.
Anmerkung: Aufgrund des Rechenfehlers bei der Modellierung der Polynomfunktion von Hand ist die Funktion nur bedingt mit den anderen Funktionen vergleichbar.
Mathematische Grundlagen für Zyklus 3
[Bearbeiten]Abstand
[Bearbeiten]
Der Abstand gibt die kürzeste Entfernung zwischen zwei geometrischen Elementen, z.B. zwei Punkten, einem Punkt und einer Gerade, zwei parallelen Geraden oder einem Punkt und einer Ebene, an.
Betrachtet man einen Punkt P und eine Gerade g in der Ebene, so ist der Abstand zwischen P und g die Länge der kürzesten Strecke zwischen der Geraden g und dem Punkt P. Die kürzeste Strecke ist hierbei immer die Strecke, die senkrecht auf der Geraden g steht und den Punkt P enthält. Man kann diese Strecke bestimmen, indem man als Hilfsgerade das Lot f von P auf g fällt. Die gesuchte Strecke ist die Strecke PA, die von P zum Schnittpunkt A von f und g verläuft. Diese Strecke ist eindeutig bestimmt, da es genau eine Lotgerade von P auf g gibt. Der gesuchte Abstand ist die Länge der Strecke h = PA.
Betrachtet man einen Punkt P und eine Ebene im Raum, so ist der Abstand auch hier wieder die kürzeste Strecke zwischen dem Punkt P und der Ebene. Diese Strecke lässt sich auch in diesem Fall durch eine Hilfsgerade bestimmen, die senkrecht auf der Ebene steht und durch den Punkt P verläuft. Die gesucht Strecke ist die Strecke, die vom Punkt P zum Durchstoßpunkt der Hilfsgerade in der Ebene läuft. Der gesuchte Abstand ist die Länge dieser Strecke.
Dreidimensionale Funktionen
[Bearbeiten]Eine dreidimensionale Funktion ist eine mathematische Funktion, die Elemente des in die Menge der reellen Zahlen abbildet. Die Elemente der Definitionsmenge kann man hierbei z.B. als Punkte mit (Punkte in der Ebene) verstehen. Die Funktionswerte, abhängig von den Variablen und , werden oft mit bezeichnet und lassen sich z.B. als Höhe interpretieren. So lassen sich z.B. Höhenprofile von Landschaften darstellen.
Beschreibung von Flächen in der Ebene
[Bearbeiten]Um dreidimensionale Funktionen abschnittsweise zu definieren, ist es erforderlich, die Ebene in Abschnitte einzuteilen und diese Abschnitte durch mathematische Bedingungen zu beschreiben.
Eine einfache Möglichkeit, rechteckige Flächen in der Ebene zu beschreiben, ist das Kreuzprodukt. Im zweidimensionalen Koordinatensystem lässt sich eine Fläche A, die alle Punkte mit und enthält, darstellen als .
In untenstehendem Beispiel bildet das grüne Quadrat die Fläche .
Darüber hinaus ist es durch Aufnahme weiterer Bedingungen möglich, dreieckige Teilflächen eines Rechtecks zu beschreiben. Hierfür benötigt man die Funktionsvorschrift der Geraden, durch die das Dreieck beschrieben wird. In untenstehendem Beispiel soll das grüne Quadrat durch die orangene Gerade in zwei Dreiecke geteilt werden. Die orangene Gerade hat die Funktionsvorschrift .
Die blau schraffierte Fläche A beinhaltet alle Punkte, die unterhalb oder auf der orangenen Geraden liegen, d.h. deren y-Koordinate kleiner oder gleich ist. Die Fläche A lässt sich somit beschreiben als .

Matrizenrechnung
[Bearbeiten]Matrizenaddition
[Bearbeiten]Matrizen, deren Zeilen- und Spaltenanzahl übereinstimmen, können komponentenweise addiert werden, wie das folgende Beispiel zeigt:
Gegeben seien die Matrizen und mit jeweils zwei Zeilen und drei Spalten. Es gilt:
Skalarmultiplikation
[Bearbeiten]Matrizen können mit einem Skalar multipliziert werden. Hierbei wird jeder Eintrag der Matrix mit dem Skalar multipliziert:
Gegeben seien die Matrix und der Skalar . Es gilt:
Subtraktion von Matrizen
[Bearbeiten]Eine Subtraktion von Matrizen ist nicht eigens definiert, lässt sich jedoch durch Hintereinanderausführung von Skalarmultiplikation und Matrizenaddition darstellen. Um zwei Matrizen zu subtrahieren, wird zuerst die zu subtrahierende Matrix (Subtrahend) mit dem Skalar multipliziert. Anschließend kann man diese Matrizen addieren. Die hierbei angewandte Vorgehensweise lässt sich folgendermaßen beschreiben: .
Folgendes Beispiel veranschaulicht dies:
Gegeben seien die Matrizen und . Es gilt:
Gaußsche Summenformel
[Bearbeiten]Mithilfe der Gaußschen Summenformel lässt sich die Summe der ersten natürliche Zahlen berechnen. Sie lautet:
Modellierungszyklus 3 - Niveau Uni
[Bearbeiten]Ziele
[Bearbeiten]In diesem Modellierungszyklus sollen die Rückenformen mehrerer Personen verglichen werden. Ziel ist es, Stellen zu identifizieren, an denen sich die Rücken verschiedener Personen stark unterscheiden. In der Modellierung des Schulranzens könnten solche Stellen besonders gepolstert werden, um eine bestmögliche Anpassung des Schulranzens an den Rücken zu ermöglichen. Analog könnten Stellen mit hoher Übereinstimmung zwischen verschiedenen Personen mit weniger Polster versehen werden, um an diesen Stellen eine bessere Kraftübertragung vom Rucksack auf den Rücken zu ermöglich.
Datenerhebung Rückenform
[Bearbeiten]Zur funktionalen Beschreibungen von Rückenformen wurden Messwerte der Rückenform von vier Studierenden erhoben. Dazu wurden die Testpersonen mit ca. 20 bis 30 cm Entfernung vor eine Wand gestellt, an der ein quadratisches Raster mit einer Seitenlänge von 5 cm befestigt war. Der Rücken der Testpersonen zeigte hierbei zur Wand. Eine zweite Person hat an den Kreuzungspunkten des Rasters den Abstand vom jeweiligen Kreuzungspunkt an der Wand zum Rücken der Testperson gemessen. Hierbei wurde darauf geachtet, dass eine senkrechte Linie des Rasters entlang der Wirbelsäule der Testpersonen verläuft. Die obersten Messwerte wurden auf Höhe der Schultern / des Beginns der Brustwirbelsäule genommen. Die untersten Messwerte wurden ca. auf Höhe der Beckenknochen genommen. Auf diese Weise erhält man Messwerte, die ein Negativ des tatsächlichen Rückens beschreiben, da der Abstand zwischen Wand und Rücken gemessen wurde. Die so erhobenen Daten sind unter Rohdaten aufgeführt.

Um die tatsächliche Form des Rückens zu erhalten, wurden die gemessenen Werte im Anschluss "umgekehrt", d.h. es wurde der Abstand des Rückens von einer gedachten senkrechten Ebene gegenüber der Wand durch Differenzbildung bestimmt. Dies hat zur Folge, dass der modellierte Rücken später auf einer gewissen Höhe ungleich Null beginnt, was jedoch im ersten Schritt noch nicht von Bedeutung ist. Beim Vergleich der Rückenformen wird hierauf nochmal eingegangen (siehe Vergleich der Rückenformen der Testpersonen). Folgende Matrizen enthalten die so berechneten "Positiv-Werte" für das dreidimensionale Rückenprofil:
| Person 1 | Person 2 | Person 3 | Person 4 |
|---|---|---|---|
Beschreibung des Rückens durch Funktionen
[Bearbeiten]In diesem Abschnitt wird erklärt, wie aus den gemessenen Werten des Rückens dreidimensionale Funktionen bestimmt wurden, die die Rückenform beschreiben. Der Einfachheit halber wird dies beispielhaft mit Werten eines gröberen Rasters gezeigt. Es handelt sich um Messwerte im Abstand von 10 cm auf einer Gesamtfläche von 20 cm x 40 cm. Folgende Messwerte wurden dazu erhoben:

Nebenstehende Abbildung zeigt das Raster dieser Messungen und die jeweiligen Messwerte an den entsprechenden Messpunkten.
Die Rückenfläche wird entsprechend des Rasters in acht Quadrate mit der Seitenlänge 10 cm eingeteilt, jedes Quadrat wird wiederum entlang einer Diagonalen in zwei Dreiecke geteilt. So ergeben sich in dieser Beispielrechnung 16 Dreiecke. Hintergrund dieser Vorgehensweise ist, dass drei Punkte im Raum genau eine Ebene aufspannen, die im jeweiligen Bereich die Rückenform beschreibt. Würde man statt Dreiecken Vierecke verwenden, könnte es passieren, dass ein Messwert nicht in der jeweiligen Ebene liegt und daher nicht in der Modellierung berücksichtigt wird. Ein Quadrat kann entlang seiner zwei Diagonalen in zwei verschiedene Dreiecke geteilt werden. Entsprechend gibt es verschiedene Möglichkeiten, wie die Dreiecke auf der gesamten Rückenform angeordnet werden können, die im Kapitel Bewertung, Modellierungsalternativen und Optimierung erläutert werden. In dieser Beispielrechnung wird die Vorgehensweise für beide Diagonalen gezeigt. Der Ursprung des Koordinatensystems wird in den folgenden Berechnungen stets an der linken unteren Ecke des Rechtecks angesetzt, um nur mit positiven Zahlen zu rechnen.
In den folgenden Abschnitten wird erläutert, die die Funktionsvorschriften für die unteren beiden Quadrate (siehe Abbildung rechts) ermittelt werden.
Das erste Quadrat umfasst die Fläche und wird durch die Diagonale in die Dreiecke und geteilt. Folgende Mengen beschreiben die Flächen der Dreiecke:

- Dreieck 1 (unten):
- Dreieck 2 (oben):
Das zweite Quadrat umfasst die Fläche und wird durch die Diagonale in die Dreiecke und geteilt. Folgende Mengen beschreiben die Flächen der Dreiecke:
- Dreieck 3 (unten):
- Dreieck 4 (oben):
Nebenstehende Abbildung zeigt die Positionierung der betrachteten Dreiecke bis .
Dreieck 1
[Bearbeiten]
Jeden Punkt innerhalb des Dreiecks kann man ausgehend vom Stützpunkt als Linearkombination der Vektoren und darstellen:
, wobei und im Intervall liegen, falls .
Löst man dieses LGS nach und auf, erhält man .
Die gesuchte Funktion wird im Folgenden der Einfachheit halber mit bezeichnet. Zur Berechnung der Funktionsvorschrift benötigt folgende Werte, die man aus der obenstehenden Matrix ablesen bzw. berechnen kann:
- Höhe des Stützpunkts :
- Höhendifferenz in x-Richtung:
- Höhendifferenz in y-Richtung:
Daraus ergibt sich folgende Funktionsvorschrift: .
Folglich wird der Rücken im Dreieck beschrieben durch die Funktion , falls .
Dreieck 2
[Bearbeiten]
Fast analog erfolgt die Bestimmung der Funktionsvorschrift für die weiteren Dreiecke.
Unterschiedlich ist lediglich die Position des Stützpunktes und die Richtung der Vektoren und . Entsprechend ergibt sich:
und folglich
.
Die benötigten Werte sind:
- Höhe des Stützpunkts :
- Höhendifferenz in x-Richtung:
- Höhendifferenz in y-Richtung:
Schließlich erhält man .
Folglich wird der Rücken im Dreieck beschrieben durch die Funktion , falls .
Dreieck 3
[Bearbeiten]
- Stützpunkt:
- Vektoren und
- Höhe des Stützpunkts :
- Höhendifferenz in x-Richtung:
- Höhendifferenz in y-Richtung:
Folglich wird der Rücken im Dreieck beschrieben durch die Funktion , falls .
Dreieck 4
[Bearbeiten]
- Stützpunkt:
- Vektoren und
- Höhe des Stützpunkts :
- Höhendifferenz in x-Richtung:
- Höhendifferenz in y-Richtung:
Folglich wird der Rücken im Dreieck beschrieben durch die Funktion , falls .
Zwischenfazit
[Bearbeiten]Insgesamt wurden auf diese Weise folgende Funktionen von Hand bestimmt:
Händisch bestimmte Funktionen für die Rückenform Bezeichnung Dreieck Definitionsbereich Funktionsvorschrift Bereich x-Werte Bereich y-Werte Bedingung Diagonale
Folgende Abbildung zeigt die vier Dreiecke, die so zur Beschreibung des unteren Rückens ermittelt wurden.

Bestimmung der Funktionen mit wxMaxima
[Bearbeiten]Um die Bestimmung der Funktionen der weiteren Dreiecke zu erleichtern, wurde eine Datei in Maxima erstellt, die bei Eingabe der Messwerte des Rückens die Funktionsvorschriften bestimmt. Hierbei wurde folgendermaßen vorgegangen:
- Eingabe: Matrix A mit Messwerten ("Positiv-Werte"), wobei die Zeilen absteigend einzugeben sind (d.h. die unteren Messwerte werden zuerst eingegeben und die oberen Messwerte zuletzt). Dies liegt daran, dass der Ursprung des Koordinatensystems an die rechte untere Ecke des Rückens angelegt wurde.
- Mithilfe des "block"-Befehls wurde eine Funktion programmiert, die den Namen "Höhe(A)" trägt.
Die Funktion beginnt mit einigen allgemeinen Berechnungen:
- Im ersten Schritt werden in eckigen Klammern die lokalen Variablen definiert.
- Die Datei bestimmt die Abmessungen der eingegebenen Matrix (Zeilen- und Spaltenanzahl) und berechnet daraus die Anzahl der Dreiecke in x- und y-Richtung (jeweils eines weniger als die Anzahl der Messwerte).
- Unter der Bezeichnung "s" wird die Schrittweite / Intervalllänge der Messungen definiert (diese muss entsprechend der Messdaten von Hand im Quellcode geändert werden).
Es folgen vier einander ähnliche Abschnitte für die verschiedenen Arten der Ausrichtung der Dreiecke (vgl. Dreiecke bis in obenstehenden Berechnungen). Die Datei ist so angelegt, dass die Rückenfläche parallel zur y-Achse in zwei Teile ("linke Hälfte" und "rechte Hälfte") geteilt wird. Die Quadrate der linken Hälfte werden wie Quadrat 1 (s.o.) durch die Diagonale von oben links nach unten rechts in je zwei Dreiecke geteilt, die Quadrate der rechten Hälfte werden wie Quadrat 2 (s.o.) durch die Diagonale von unten links nach oben rechts in je zwei Dreiecke geteilt. Der Aufbau eines solchen Abschnitts wird im Folgenden skizziert:
- Jeder Abschnitt beginnt mit einer Überschrift, die bei Ausführung der Datei ausgegeben wird, dies erfolgt über den Befehl "print".
- Es folgen zwei ineinander verschachtelte for-Schleifen für die Dreiecke in x- bzw. y-Richtung. Die äußere for-Schleife für die y-Richtung läuft immer über die gesamte Länge des Rechtecks, die innere for-Schleife für die x-Richtung läuft entsprechend der Teilung des Rechtecks in die rechte und linke Hälfte jeweils nur über die halbe Breite (von 1 bis zur Mitte bzw. von der Mitte bis zum Ende).
- In jedem Schritt der Schleifen wird der Stützpunkt definiert.
- Ein beliebiger Punkt im Dreieck wird allgemein durch das Gleichungssystem beschrieben, das im nächsten Schritt nach und aufgelöst wird. Der Einfachheit halber wurden in der Programmierung in Maxima und als und bezeichnet.
- Die Gleichung aus den Termen für und , den in der Matrix A stehenden Werten für die Rückenhöhe und den jeweils passenden Vektoren und wird aufgestellt. Um auf die korrekten Werte in der Matrix A zugreifen zu können, musste an einzelnen Stellen auf Einträge der transponierten Matrix zugegriffen werden.
- Die Ausgabe der Funktion erfolgt über den "print"-Befehl. Ausgegeben wird der jeweilige Definitionsbereich der Funktion und die zugehörige Funktionsvorschrift (Lösung der Gleichung aus dem vorherigen Schritt).
Insgesamt gibt die Datei so für alle Dreiecke die entsprechende Funktion aus. Die Ausgabe ist entsprechend der vier Abschnitte sortiert nach "links, untere Dreiecke", "links, obere Dreiecke", "rechts, untere Dreiecke" und "rechts, obere Dreiecke". Die Ausgabe der Funktionen wurde so angelegt, dass diese nach nur geringfügiger Modifikation in GeoGebra eingegeben werden kann, um die Funktionen zu visualisieren. An relevanten Stellen im Quellcode der Datei wurden durch /* ... */ gekennzeichnete Kommentare eingefügt, die die Vorgehensweise beschreiben und bei der Ausführung der Datei unbeachtet bleiben.
Folgende Abbildung zeigt einen Ausschnitt des Quellcodes der Maxima-Datei für obenstehende Messwerte des 10cm-Rasters. Zu sehen sind die Eingabe der Matrix A, der allgemeine Teil der Funktion und der erste Abschnitt der Berechnung der Funktionsvorschriften.

Führt man die Funktion mit der eingegebenen Matrix A aus, erhält man folgende Funktionen für die Beschreibung des gesamten Rückens:
 |
 |
Entnimmt man der Ausgabe aus wxMaxima die Funktionen der Dreiecke bis (s.o.), erhält man folgende Funktionen:
Von wxMaxima bestimmte Funktionen für die Rückenform Bezeichnung Dreieck Definitionsbereich Funktionsvorschrift Bereich x-Werte Bereich y-Werte Bedingung Diagonale
Mithilfe von Termumformungen lässt sich zeigen, dass die Funktionsvorschriften, die von wxMaxima berechnet wurden, mit den von Hand berechneten Funktionsvorschriften übereinstimmen.
Die Funktionen können nun mithilfe von GeoGebra 3D dargestellt werden. Folgende Abbildung zeigt den gesamten Rücken der obenstehenden Messwerte, die im Abstand von jeweils 10 cm aufgenommen wurden:

Bewertung, Modellierungsalternativen und Optimierung
[Bearbeiten]Bei obenstehender Bestimmung der Funktionen zur Beschreibung des Rückens wurde festgelegt, dass der Rücken entlang einer vertikal verlaufenden Mittellinie in zwei Hälften geteilt wird. Weiterhin wurde festgelegt, dass die Quadrate in der linken Hälfte des Rückens durch die von oben links nach unten rechts verlaufende Diagonale in je zwei Dreiecke geteilt werden und die Quadrate in der rechten Hälfte des Rückens durch die von unten links nach oben rechts verlaufende Diagonale in je zwei Dreiecke geteilt werden. Dadurch entsteht in des Modellierung des Rückens eine V-Form. Diese Festlegung lässt sich durch den Aufbau des Rückens erklären: der menschliche Rücken wird längs durch die Wirbelsäule in zwei Hälften geteilt, daher ist es sinnvoll, auch im Modell so vorzugehen. Die Ausrichtung der Dreiecke in V-Form hat zur Folge, dass man mögliche Höhenunterschiede im Bereich der Wirbelsäule und Ähnlichkeiten / Symmetrien zwischen den beiden Rückenhälften gut erkennen kann.
Zur Ausrichtung der Dreiecke in V-Form gäbe es zahlreiche Alternativen. Bei Verwendung von ausschließlich parallelen Diagonalen in den verschiedenen Quadraten ergibt sich z.B. ein Streifen-Muster. Denkbar wäre auch ein Rauten-Muster, das sich durch Vertauschung der Diagonalen in jeder zweiten Reihe ergibt (siehe Abbildung).

Das Rauten-Muster hat den Vorteil, dass einzelne Erhebungen oder Senken am Rücken gut sichtbar sind, hätte aber in der technischen Umsetzung in wxMaxima eine Verdopplung der Fallunterscheidungen erfordert, worauf an dieser Stelle verzichtet wurde. Ein Nachteil bei dieser Form ist, dass man den Verlauf der Rückenform insgesamt aufgrund der mehrfach wechselnden Richtungen der Diagonalen evtl. nicht so gut erkennen kann wie bei der V-Form.
Beim Streifen-Muster ist anzunehmen, dass man die Ähnlichkeiten / Symmetrie zwischen den beiden Rückenhälften nicht so gut erkennen könnte, weshalb diese Variante nicht weiter betrachtet wird.
Zum Vergleich der verschiedenen Modelle wurden exemplarisch für das obenstehende 10cm-Raster auch die Funktionsvorschriften im Rauten- und Streifen-Muster bestimmt. Folgende Abbildung zeigt die drei Formen im Vergleich:
| V-Muster | Rautenmuster | Streifenmuster |
|---|---|---|
 |
 |
 |
Bei der Programmierung der Datei in wxMaxima gibt es einige Aspekte, die man auch anders hätte lösen können. Diese werden im Folgenden kurz angesprochen und mögliche Alternativen und Optimierungsideen vorgestellt.
- Ziel war es, eine Datei zu programmieren, die mit einer möglichst einfachen Eingabe auskommt. Aus diesem Grund wurde entschieden, lediglich die gemessenen Rückenhöhen in die Eingabe-Matrix einzutragen. Dies hat zur Folge, dass die Intervalllänge an anderer Stelle festgelegt werden muss.
- Alternativ wäre es möglich, alle Koordinaten der Messpunkte als Eingabe zu verwenden. Eine gesonderte Eingabe der Intervalllänge wäre in diesem Fall nicht erforderlich, da die x- und y-Koordinaten der jeweiligen Messpunkte schon in der Eingabe enthalten sind und nicht berechnet werden müssen. Jedoch wäre in diesem Fall die Eingabe-Matrix sehr komplex geworden. Aus diesem Grund wurde diese Möglichkeit bei der Modellierung verworfen.
- Eine zweite Möglichkeit wäre gewesen, die Eingabe als Liste anzulegen, die zum einen die Matrix der Messwerte beinhaltet und als zweiten Eintrag den Wert für die Intervalllänge. Dies hätte die Eingabe nur leicht komplizierter gemacht, würde aber ermöglichen, dass die Intervalllänge nicht im Quellcode manuell verändert werden muss. Hierbei handelt es sich um eine nützliche Modifikation, in bei weiteren Anpassungen evtl. berücksichtigt werden könnte.
- Aufgrund der Festlegung, dass der Ursprung des Koordinatensystems an der rechten unteren Ecke des Rückens angelegt wird, ist es bei der Eingabe der Matrix notwendig, die Zeilen in absteigender Reihenfolge einzugeben (s.o.). Dies hängt damit zusammen, dass die Variablen der for-Schleifen jeweils beim Wert 1 (bzw. in der Mitte des Rückens) beginnen und bis zur Anzahl der benötigten Dreiecke laufen. Da mithilfe dieser Variablen auf die Einträge der Matrix zugegriffen werden sollte, muss die Matrix in umgekehrter Reihenfolge eingegeben werden.
- Um die Benutzung der Datei zu vereinfachen und Anwendungsfehler aufgrund falscher Eingaben zu vermeiden, wäre es sinnvoll, die Datei so zu variieren, dass die Matrix vor der Eingabe nicht manuell verändert werden muss. Dies könnte z.B. durch einen Zwischenschritt erfolgen, in dem die Matrix innerhalb der Funktion passend umsortiert wird. Alternativ könnte man den Ursprung des Koordinatensystems an die obere rechte Ecke legen und den Rücken von oben nach unten durchlaufen.
- Die Ausgabe der Funktionen wurde so angelegt, dass die Funktionen mit nur wenigen Anpassungen in GeoGebra übertragen werden können, um die Rückenform zu plotten. Dies ist in der aktuellen Version jedoch noch immer mit etwas Aufwand verbunden. Kopiert man die Funktionen in ein Textdokument, befinden sich die Anführungszeichen, die in der wxMaxima-Datei für Textausgabe sorgen, im Text - diese kann man jedoch mit der "Suchen und ersetzen"-Funktion von Textverarbeitungsprogrammen entfernen. Um die Funktionen in GeoGebra zu visualisieren, ist es aktuell erforderlich, jede Funktion einzeln in eine GeoGebra-Datei zu kopieren, was ab einer gewissen Anzahl an Funktionen sehr ungünstig ist.
- Eine Optimierung der wxMaxima-Datei könnte darin bestehen, die Ausgabe der Funktionen so zu gestalten, dass für den gesamten Rücken eine Funktion ausgegeben wird, die abschnittsweise auf den einzelnen Quadraten definiert ist. So könnte die Funktion zur Beschreibung des gesamten Rückens in einem Schritt z.B. in eine GeoGebra-Datei kopiert werden und es müsste nicht mehr für jedes Dreieck eine Funktion in GeoGebra eingefügt werden. Um dies zu realisieren, müssen die in den einzelnen Schritten der for-Schleifen bestimmten Funktionen mit Indizes versehen werden. Die Ausgabe der Funktion würde dann nicht mehr innerhalb der for-Schleifen erfolgen, sondern nach Ablauf der Schleifen. Durch Zugreifen auf die einzelnen Variablen durch z.B. zwei weitere for-Schleifen könnte man dann die Ausgabe so anlegen, dass eine abschnittsweise definierte Funktion ausgegeben wird.
- Im Rahmen der Programmierung der wxMaxima-Datei wurde testweise eine 9x15-Matrix bestehend aus Messwerten im Abstand von je 4 cm eingegeben. Dies führt zu einer Einteilung des Rückens in Quadrate und entsprechend Dreiecke. Zur Berechnung dieser 224 Funktionen hat das Programm mehrere Minuten gebraucht und sich dabei mehrfach aufgehängt. Auch die Übertragung der Funktionsvorschriften in z.B. eine GeoGebra-Datei ist bei einem so feinen Raster sehr aufwändig und wurde nicht vollständig durchgeführt. Es zeigt sich, dass wxMaxima für Berechnungen in diesem Umfang evtl. nicht optimal geeignet ist. Stattdessen könnte man auf leistungsstärkere Programme zur Datenverarbeitung, wie z.B. Octave zurückgreifen. Folgende Abbildung zeigt die unteren 12 cm des Rückenmodells im 4er-Raster:

Darstellung der Rückenformen der Testpersonen
[Bearbeiten]Berechnung mit wxMaxima und Visualisierung in GeoGebra
[Bearbeiten]Unter Rohdaten sind die Messwerte zu finden, die die Rückenform der Testpersonen in Abständen von 5 cm beschreiben. Diese wurden im Kapitel Datenerhebung Rückenform umgerechnet ("Positiv-Werte" statt "Negativ-Werte").
Zur Eingabe der Werte in wxMaxima ist es erforderlich, die Zeilen der Matrizen in umgekehrter Reihenfolge einzugeben. Führt man diese Umsortierung durch, erhält man folgende Matrizen:
| Person 1 | Person 2 | Person 3 | Person 4 |
|---|---|---|---|
Folgende Abbildung zeigt die Funktionen für Testperson 1, die von wxMaxima bestimmt wurden, und eine Visualisierung dieser Funktionen in GeoGebra 3D.
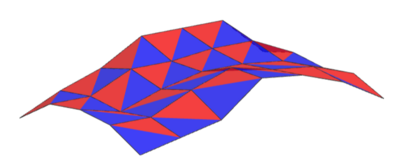
Analog lassen sich diese Funktionen auch für die anderen drei Testpersonen berechnen und in GeoGebra darstellen.
Bei der Visualisierung dieser Modelle in GeoGebra kam es mit wachsender Anzahl der Funktionen immer öfter zu Anzeigeproblemen in GeoGebra. Nebenstehende Abbildungen zeigen beispielhaft solche fehlerhaften Darstellungen: Zu sehen sind das Rückenmodell von Testperson 1, das auch obenstehende Abbildung zeigt, und der untere Bereich des Rückens im 4er-Raster. Die weißen Flächen in der fehlerhaften Darstellung müssten eigentlich wie oben in rot und blau gefärbt sein und die berechneten Dreiecke darstellen.


Aufgrund dieses sich häufenden Fehlers wird im Folgenden eine alternative Methode zur Visualisierung der Modelle beschrieben.
Visualisierung in Octave
[Bearbeiten]Mithilfe des Befehls "mesh" und der Matrix mit den Messwerten lässt sich folgende Darstellung der Rückenform von Testperson 1 erstellen:

Im Gegensatz zur Darstellung in GeoGebra lässt sich diese Darstellung ausschließlich mit den Messwerten erstellen, die Funktionsvorschriften sind hierfür nicht erforderlich. Die Erzeugung dieser Abbildung ist weniger zeitaufwändig als mit GeoGebra, da sie von Octave automatisiert erstellt wird. Ein Nachteil ist, dass man in der Darstellung von Octave die Einteilung des Rückens in die von wxMaxima berechneten Dreiecke nicht erkennen kann.
Vergleich der Rückenformen der Testpersonen
[Bearbeiten]Vorgehensweise bei der Berechnung
[Bearbeiten]Um die Rückenformen der Testpersonen miteinander zu vergleichen, war ursprünglich geplant, mithilfe von wxMaxima pro Testperson eine Funktion zu bestimmen, daraus jeweils die Differenzfunktionen zwischen den einzelnen Testpersonen zu berechnen und die Maxima dieser Funktionen zu identifizieren. An diesen Stellen liegt zwischen den Rückenformen verschiedener Personen eine große Abweichung vor, weshalb diese Stellen am Rucksack mit viel elastischen Material ausgefüllt werden müssten.
Diese Vorgehensweise wird aufgrund weiterführender Überlegungen und Ideen während der Modellierung nicht weiter verfolgt, könnte aber mithilfe einer Anpassung der Ausgabe in wxMaxima umgesetzt werden. Hintergrund ist, dass bei dieser Vorgehensweise für den Vergleich von zwei Personen je eine Differenzfunktion bestimmt und Maximalstellen identifiziert werden müsste. Beim Vergleich von vier Personen wären dies Funktionen (Person 1 mit Person 2-4, Person 2 mit Person 3-4 und Person 3 mit Person 4). Bei Personen sind es allgemein Funktionen, mit denen die Berechnungen durchgeführt werden müssten. Schon beim Vergleich der Rückenformen von 10 Personen müsste man diese Berechnungen mit 36 Funktionen durchführen und die Ergebnisse vergleichen, bei 20 Personen schon mit 171 Funktionen. Um diesen großen Rechenaufwand bei großem zu umgehen, wird nach einer Vorgehensweise gesucht, die mit weniger Berechnungen auskommt.
Dazu wird versucht, statt mit den Funktionen nur mit den Matrizen der Messwerte zu rechnen. Im ersten Schritt wird an jedem Messpunkt aus den Messwerten der vier Testpersonen ein Mittelwert gebildet. Diese Mittelwerte werden in einer Matrix zusammengefasst, die als Norm-Rückenform in den späteren Berechnungen verwendet wird.
Zur Berechnung dieser Mittelwerte ist es nötig, wie unter Datenerhebung Rückenform bereits erwähnt, die Messwerte der Testpersonen auf ein einheitliches Niveau zu skalieren. Bei der Datenerhebung wurden die obersten Messwerte auf Höhe der Schultern / des Beginns der Brustwirbelsäule genommen. Aus diesem Grund wird diese Messreihe, konkret der mittlere Messpunkt auf Höhe der Wirbelsäule, als Vergleichspunkt in allen vier Matrizen auf die gleiche Höhe gesetzt. Dies wird durch Addition / Subtraktion der einzelnen Matrizen erreicht, wobei die absolute Höhe nicht relevant ist. Die in der Höhe angepassten Matrizen werden mit bezeichnet.
Die Daten, die den gemittelten Rücken (Durchschnittsrücken) beschreiben, sind jeweils die Mittelwerte der einzelnen Messwerte. Diese lassen sich in Octave berechnen, indem die vier Matrizen addiert werden und die Summe anschließend durch vier geteilt wird. Die Matrix mit den Mittelwerten wird mit bezeichnet.
Im nächsten Schritt wird von der Mittelwertsmatrix jeweils die Differenz zu den Matrizen bis berechnet und als bis bezeichnet.
Die so berechneten Werte werden im Anschluss in eine Tabellenkalkulation (LibreOffice Calc) übertragen. Hierfür nutzt man den Befehl "odswrite('Wunschname.ods',zu exportierende Variable)", der eine Datei mit den Daten aus Octave erstellt, die den Wunschnamen trägt und die Daten der genannten Variable beinhaltet.
In der so erstellten Tabelle werden mithilfe der Funktion "Bedingte Formatierung" folgende Regeln aufgestellt, um die Werte in den einzelnen Zellen zu formatieren. Die Regeln werden in absteigender Reihenfolge vom Programm angewandt:
| Bedingung an den Zellwert | Formatvorlage (Hintergrundfarbe) |
|---|---|
| ist gleich | blau |
| ist gleich | rot |
| ist gleich | gelb |
| ist gleich | gelb |
| ist zwischen und | grün |
| ist zwischen und | gelb |
| ist zwischen und | gelb |
| ist größer | blau |
| ist kleiner | rot |
Hierbei gelten folgende Annahmen:
- Stellen mit weniger als 0,5 cm Abweichung vom Durchschnittsrücken sind unproblematisch (grün) und werden nicht weiter betrachtet.
- Stellen mit einer Abweichung zwischen 0,5 (eingeschlossen) und 1 (ausgeschlossen) zwischen Testperson und Durschnitt sind ggfs. relevant und werden mit gelb gekennzeichnet.
- Stellen mit einer Abweichung von 1 oder mehr sind relevant und werden mit rot (negativ) oder blau (positiv) gekennzeichnet.
Anhand der farblichen Hervorhebung sollen Stellen identifiziert werden, an denen bei mehreren Testpersonen Abweichungen vom Durchschnittsrücken vorliegen. Diese Stellen werden in der Modellierung des Schulranzens mit Polster versehen. Im folgenden Kapitel wird hierfür beschrieben, wie die jeweiligen Werte interpretiert werden und was diese für die Praxis bedeuten.
Vorgehensweise bei der Interpretation der Ergebnisse
[Bearbeiten]Ein positiver Wert in einer Differenzmatrix bedeutet, dass der Rücken der Testperson an dieser Stelle niedriger ist als der Durchschnittsrücken, ein negativer Wert gibt Stellen an, an denen der Rücken der Testperson höher als der Durchschnittsrücken ist.
Es bietet sich an, die Form des Schulranzens an die Form des "Durchschnittsrückens" anzupassen. Wenn man die Rückseite des Rucksacks aus festem Material herstellt, könnte man an einzelnen Stellen folgende Anpassungen vornehmen:
- An Stellen, an denen einige Testpersonen positive Abweichungen aufweisen (d.h. ihr Rücken ist niedriger als der Durchschnittsrücken), könnte man zusätzliche Polster anbringen, die sich bei den betroffenen Personen an die Rückenform anpassen. Bei Personen, die an diesen Stellen keine Abweichungen aufweisen, würde sich das Polster an den betroffenen Stellen zusammendrücken, die Form des Rucksacks entspricht dann wieder dem Durchschnittsrücken.
- An Stellen, an denen einige Testpersonen negative Abweichungen aufweisen (d.h. ihr Rücken ist höher als der Durchschnittsrücken), könnte man das feste Material an der Rückseite des Rucksacks durch Polster ersetzen. In diese Polsterflächen könnten sich außergewöhnliche Erhebungen am Rücken der betroffenen Personen einfügen. Bei Personen, die an diesen Stellen keine Abweichungen aufweisen, bleibt das Polster in der Form des Durchschnittsrückens und verformt sich nicht.
- An Stellen, an denen in der Gruppe der Testpersonen sowohl positive als auch negative Abweichungen vorkommen, könnte man entsprechend beide Arten von Polster anbringen, um eine optimale Anpassung an die verschiedenen Rückenformen zu ermöglichen.
Es ist jedoch darauf zu achten, dass es genügend Stellen gibt, an denen der Rucksack nicht gepolstert ist. Diese sind erforderlich, damit die wirkenden Kräfte entlang des Rückens bestmöglich verteilt werden können und nicht ausschließlich durch die Rucksackträger auf die Schultern übertragen werden. Es ist also ein Kompromiss zu finden zwischen flexibler Anpassung an die verschiedenen Rückenformen und Stabilität und Formfestigkeit des Rucksacks für gute Kraftverteilung.
Berechnungen mit den vorliegenden Messwerten
[Bearbeiten]Die in der Höhe angepassten Matrizen bis sind in der folgenden Übersicht zu sehen ( zeigt die Werte von Person 1, die Werte von Person 2, etc.). Der Vergleichspunkt ist der mittlere Wert der ersten Zeile.
 |
 |
Daraus ergibt sich die Matrix , die den Durchschnittsrücken berschreibt:

Klar ist, dass der Vergleichspunkt, der in allen vier Matrizen den Wert 5 hat, auch in der Matrix mit den Mittelwerten (mit bezeichnet) den Wert 5 hat.
Man erhält folgende Differenzmatrizen , die an der Stelle des Vergleichspunktes alle den Wert 0 haben:
 |
 |
Überträgt man diese Werte in eine Tabelle (LibreOffice Calc) und formatiert sie entsprechend der obenstehenden Angaben, erhält man folgende Ansicht:

Interpretation der Ergebnisse
[Bearbeiten]Betrachtet man die Tabelle, fallen folgende Punkte auf:
- Bei Person 1 liegen sehr viele negative Abweichungen vor, d.h. der Rücken dieser Person ist an vielen Stellen höher als der Durchschnittsrücken.
- Bei den Personen 2-4 liegen vor allem an den Rändern vereinzelte Abweichungen in positive Richtung vor, d.h. an den Rändern sind die Rücken dieser Personen niedriger als der Durchschnittsrücken.
Entsprechend der unter Vorgehensweise bei der Interpretation der Ergebnisse notierten Überlegungen, folgt daraus für die Modellierung des Schulranzens:
- Entlang der Rückenfläche des Rucksacks müsste der Rucksack großflächig aus Polster hergestellt werden, um eine Anpassung des Rucksacks an den Rücken von Person 1 zu ermöglichen.
- An den Rändern des Rucksacks müsste zusätzliches Polster angebracht werden, um den positiven Abweichungen bei Person 2-4 gerecht zu werden.
Insgesamt müsste nach diesen Überlegungen fast überall Polster angebracht werden, da sich die Rückenformen der Testpersonen stark unterscheiden. Dies steht jedoch in Konflikt mit der Tatsache, dass einige Stellen zur Kraftübertragung von Polster freigehalten werden sollten. Welche Stellen hierfür am besten geeignet sind, d.h. an welchen Stellen am ehesten auf Polster verzichtet werden kann, ist unter Berücksichtigung weiterer Aspekte in weiterführenden Überlegungen zu untersuchen.
Zu den konkreten Messwerten der einzelnen Testpersonen lassen sich noch folgende Überlegungen anführen:
- Auffällig ist, dass nur bei Testperson 1 großflächig negative Abweichungen vorliegen. Bei Testperson 2-4 liegen dagegen entlang der Hauptfläche des Rückens kaum Abweichungen (unter 1 cm) vor. Dies lässt sich evtl. auf Messfehler oder eine auffällige Rückenform (z.B. Rundrücken / Buckel) zurückführen.
- Die positiven Abweichungen im oberen Bereich an den Rändern der Rücken von Testperson 2-4 (niedriger als der Durchschnittsrücken) lassen sich evtl. mit einem eher schmalen Brustkorb erklären.
- Bei Person 2 und 3 liegen in der rechten Rückenhälfte im oberen Bereich Abweichungen in beide Richtungen vor, die auf dem Rücken eng beieinander liegen. Möglicherweise ist diese Auffälligkeit durch unterschiedliche Schulterformen und -breiten zu erklären. Es kann z.B. vorkommen, dass bei manchen Personen die Schultern eine gerade Linie bilden, bei anderen Personen dagegen fallen die Schultern vom Hals ausgehend zu beiden Seiten nach unten ab.
Bewertung und Optimierung
[Bearbeiten]Die Ergebnisse obiger Berechnungen sind für die konkrete Modellierung eines Schulranzens aus folgenden Gründen nur bedingt aussagekräftig:
- Die Stichprobengröße ist mit vier Testpersonen sehr gering, die Ergebnisse daher nicht repräsentativ. Zur Erhebung aussagekräftiger Daten müsste eine deutlich größere Stichprobe untersucht werden. Hierbei könnte man genauer untersuchen, ob sich Abweichungen an einzelnen Stellen häufen und auffällige Rückenformen besser in die Gesamtheit einordnen.
- Die Vorgehensweise bei der Datenerhebung (Ausmessung der Rückenform mithilfe eines Maßbands) ist sehr fehleranfällig, da es kaum möglich ist, mehrere Minuten bewegungslos auf der Stelle zu stehen. Durch Festhalten z.B. am Türrahmen wurde versucht zu erreich, dass die Testpersonen möglichst wenig schwanken, jedoch sind Messungenauigkeiten nicht auszuschließen. Bei einer breiter angelegten Untersuchung von Rückenformen gilt es daher, nach genaueren Methoden zur Datenerhebung zu suchen. Denkbar wäre z.B. die Verwendung von Laser-Abstandsmessgeräten, die eine genauere und schnellere Datenerhebung mit kleineren Abständen zwischen den Messpunkten ermöglichen könnten.
- Ungünstig ist auch, dass der Durchschnittsrücken aus den gleichen Messwerten berechnet wurde, die auch zum Vergleich mit dem Durchschnittsrücken verwendet wurden. Es ist zu berücksichtigen, dass die Rückenformen der Testpersonen vermutlich weniger vom Durchschnittsrücken abweichen als in der Realität, da der Durchschnittsrücken auf Grundlage der Messwerte der Testpersonen berechnet wurde. Diese Ungenauigkeit könnte man bei weiteren Untersuchungen rechnerisch ausgleichen (vgl. z.B. die korrigierte Stichprobenvarianz). Alternativ wäre es auch denkbar, die Rückenformen von zwei Gruppen zu erheben: aus den Daten einer Gruppe wird der Durchschnittsrücken berechnet, die Daten der anderen Gruppe werden mit dem Durchschnittsrücken verglichen. Dies erfordert jedoch eine sehr große Anzahl an Testpersonen.
- Die Daten der Rückenformen, die bei den Berechnungen verwendet wurden, stammen von erwachsenen Personen. Bei der Modellierung eines Schulranzens für Jugendliche müsste man entsprechend Testpersonen im Alter der Zielgruppe verwenden. Die weitere Vorgehensweise lässt sich jedoch problemlos auf diese Altersgruppe anpassen.
- Problematisch ist zudem die graphische Auswertung der Differenzmatrizen. Diese Methode ist bei einer kleinen Stichprobenzahl gut umsetzbar, wird jedoch bei einer großen Anzahl an Testpersonen sehr unübersichtlich und die Interpretation vermutlich ungenau. In weiteren Untersuchungen sind daher Methoden zu suchen, mit denen der Vergleich der Matrizen einfacher erfolgen kann, z.B. durch die Berechnung der Streuung (vgl. dazu z.B. Normalverteilung).
Zur Modellierung eines Schulranzens spielen darüber hinaus die folgenden Aspekte eine Rolle:
- Grundsätzlich ist anzunehmen, dass ein menschlicher Rücken entlang der Wirbelsäule symmetrisch ist, weshalb Rucksäcke aus eigener Erfahrung üblicherweise symmetrisch konstruiert sind. Bei den Messergebnissen der Testpersonen zeigt sich, dass die vermutete Symmetrie des Rückens nicht überall vorliegt. Aus diesem Grund ist zu prüfen, ob eine symmetrische Modellierung eines Schulranzens angebracht ist, oder ob in der Stichprobe einheitliche Asymmetrien in der Rückenform vorliegen.
- In der Modellierung wurden die Daten von männlichen und weiblichen Testpersonen gemeinsam betrachtet. Aufgrund unterschiedlicher Körpergrößen, Rückenlängen und Schulterbreiten zwischen Mädchen und Jungen in der Pubertät wäre es auch denkbar, getrennte Rucksäcke für Mädchen und Jungen zu entwickeln, die an die jeweiligen Körpermaße besser angepasst sind als ein Rucksack für alle Geschlechter.
Verwendete Software
[Bearbeiten]Tabellenkalkulation (LibreOffice Calc)
[Bearbeiten]Mithilfe der Tabellenkalkulation LibreOffice Calc wurden die für Zyklus 1 benötigten Daten gesammelt und strukturiert. Zur Berechnung der Mittelwerte der Maße der Schulbücher wurde die Funktion MITTELWERT(Zahl 1; Zahl 2; ...) verwendet, die den Mittelwert der ausgewählten Werte berechnet. Bei der Modellierung des Quaders, der die Schulbücher und Schulhefte darstellt, konnten außerdem die Funktionen SUMME(Zahl 1; Zahl 2; ...) und MAX(Zahl 1; Zahl 2; ...) verwendet werden, die die Summe bzw. das Maximum der entsprechenden Werte ausgeben. Nützlich war zudem die Funktion SVERWEIS(Suchkriterium; Matrix; Index; Sortierte Bereichssuche), die einen bestimmten Wert in einer senkrechten Liste sucht und die Inhalte nebenliegender Zellen ausgibt. Mit dieser Funktion konnte bei der Berechnung der durchschnittlich benötigten Schulbücher pro Wochentag auf die berechneten Mittelwerte der Schulbuch-Maße zurückgegriffen werden. Der Vorteil hierbei ist, dass die einzelnen Tabellenblätter auf diese Weise miteinander verknüpft werden können und z.B. Änderungen der Messwerte direkt in den folgenden Berechnungen berücksichtigt werden.
Beim Vergleich der Rückenformen in Zyklus 3 wurde die Funktion "Bedingte Formatierung" verwendet, um die Höhe der Abweichungen zu visualisieren und so den Vergleich der Differenzmatrizen zu vereinfachen. Hierfür wurden Regeln angelegt, die beschreiben, wie die Zellen in Abhängigkeit des Zellwerts formatiert werden. Die Regeln werden dabei in absteigender Reihenfolge angewandt.
GeoGebra
[Bearbeiten]In Zyklus 1 wurden in Geogebra die einzelnen Bestandteile des Schulranzens angeordnet. So konnten zu Beginn die Grundflächen der jeweiligen Gegenstände in der Ebene auf verschiedene Weisen positioniert werden. Im Anschluss konnten die Grundflächen der Gegenstände mit dem 3D-Werkzeug "Zum Prisma extrudieren" als dreidimensionale Körper dargestellt werden. Der Rucksack, der im ersten Modellierungszyklus als Quader um die benötigten Gegenstände modelliert wurde, hat sich dann aus den jeweiligen Abmessungen ergeben und wurde ebenso erst in der Ebene und dann im Raum dargestellt. Bei der Erstellung der animierten Darstellung der Modellierung war die Wiedergabe-Funktion des Konstruktionsprotokolls von Nutzen.
In Zyklus 2, Teil a, wurden die Gegenstände ähnlich wie in Zyklus 1 neu angeordnet, hier mit dem Unterschied, dass teilweise Gegenstände gestapelt wurden, oder die quaderförmigen Prismen auf andere Flächen gestellt wurden. Es wurden Geraden aus jeweils zwei Eckpunten der hervorstehenden Gegenstände konstruiert. Mit diesen wurden, mit dem Befehl "Schnittpunkt", Schnittpunkte mit der Seitenfläche des Quaders konstruiert. In einer neuen Datei wurden diese Punkte auf einer Ebene ins Zweidimensionale Übertragen. Es wurden allgemeine Funktionen (einer Parabel und einer Exponentialfunktion) eingegeben mit undefinierten Parametern. Mit Schiebereglern konnte man die Parameter so verändern, dass die jeweilige Funktion über, aber so nah wie möglich an den Punkten liegt. Mit dem Befehl "Integral" wurde dann die Fläche unter den Funktionen in einem den Rucksack begrenzenden Intervall berechnet. Ebenfalls berechnet wurde mit "IntegralZwischen" die Fläche zwischen der rechteckigen Fläche und der Parabel berechnet, die dann von der Parabelfläche abgezogen wurde. In der ersten Datei wurde dann die Exponentialfunktion mit richtigen Parametern ins Dreidimensionale übertragen und mit dem "Wenn"-Befehl in X- und Y-Richtung eingeschränkt. Mit dem Befehl "Kurve" ließ sich die Funktion als Kurve im Raum darstellen. Mit "Punkt(<Objekt>,<Parameter>)" wurden mehrere Punkte auf der Kurve erstellt, durch die eine Polygonfläche konstruiert werden konnte, die die Seitenfläche beschränkt. Mit "Verschiebe(<Objekt>,Vektor(.,.,.))" konnte die gesamte Konstruktion der einen Rucksackseite auch auf die andere gebracht werden.
In Zyklus 2, Teil b, wurde GeoGebra verwendet, um auf der Abbildung der menschlichen Wirbelsäule die Rückenform mithilfe von Funktionen zu modellieren. Hierzu wurde die Abbildung als Hintergrundbild in die GeoGebra-Datei eingefügt. Bei dieser Vorgehensweise wurde keine Möglichkeit gefunden, die Punkte entlang der Wirbelsäule an das Bild zu binden, was zur Folge hatte, dass die Modellierung nicht zugfest ist. Es ist daher wichtig, die Abbildung zu Beginn im richtigen Maßstab einzufügen und an der richtigen Stelle zu positionieren, damit sie im weiteren Verlauf nicht mehr verschoben werden muss. Darüber hinaus wurden zur Modellierung der Rückenform mithilfe der Werkzeuge "TrendSin" und "TrendPoly" Funktionen bestimmt, die die gegebenen Punkte am besten beschreiben. Der Befehl "IntegralZwischen" wurde verwendet, um die Fläche zwischen Funktionen (Rucksack und Rücken) zu berechnen. Hierbei waren auch die Befehle "Max" und "Min" von großem Nutzen, die Maxima und Minima von Funktionen in einem gegebenen Intervall ausgeben.
In Zyklus 3 wurden die Funktionen, die die einzelnen Abschnitte des Rückens beschreiben, in GeoGebra eingegeben und die Rückenform auf diese Weise visualisiert. Hierfür wurde der "Wenn"-Befehl verwendet, der nach der folgenden Logik funktioniert:
oder [24]
Die Bedingung war in diesem Fall der Definitionsbereich einer Funktion, z.B. (das "Und"-Zeichen "" wird in GeoGebra durch "&&" eingegeben). Das "Dann Objekt" war dementsprechend die Funktionsvorschrift für diesen Bereich, z.B. . Ein "Sonst Objekt" wurde in den meisten Fällen nicht eingegeben. Eine Möglichkeit dieser Funktion im Kontext dieser Verwendung besteht z.B. darin, die Bedingungen und Funktionsvorschriften mehrerer Rückenabschnitte in einem verschachtelten "Wenn"-Befehl einzugeben.
wxMaxima
[Bearbeiten]wxMaxima wurde in Modellierungszyklus 3 genutzt, um die Funktionsvorschriften zur Beschreibung des Rückens computergestützt zu ermitteln. Folgende Funktionen und Befehle wurden hierbei verwendet:
- Matrizen eingeben und benennen: A:matrix([Einträge der ersten Zeile, mit Komma voneinander getrennt], [Einträge der zweiten Zeile, mit Komma voneinander getrennt], ...)
- Größe von Matrizen bestimmen: matrix_size(A) gibt als Liste die Zeilen- und Spaltenzahl der Matrix A aus
- Zusammenfassen von Befehlen, die nacheinander ausgeführt werden sollen: block([Auflistung der vorkommenden lokalen Variablen, durch Komma voneinander getrennt], Auflistung der auszuführenden Befehle, durch Komma voneinander getrennt)
- Befehl zur Ausgabe von Texten oder Variablen: print("Text") oder print(z)
- Gleichungen lösen: linsolve([Liste der zu lösenden Gleichungen, mit Komma voneinander getrennt], [Liste der zu bestimmenden Variablen, mit Komma voneinander getrennt])
- Zugreifen auf eine Seite einer Gleichung g: rhs(g) (greift auf die rechte Seite von g zu) und lhs(g) (greift auf die linke Seite von g zu)
- Matrizen transponieren: transpose(A)
- for-Schleife:
- Hintereinanderausführung von Befehlen, bis eine Variable (hier: a) ausgehend vom Startwert mit vorgegebener Schrittweite den Endwert erreicht hat
- Eingabe in wxMaxima: for a: Startwert step Schrittweite thru Endwert do [Liste der auszuführenden Befehle, mit Komma voneinander getrennt]
Octave
[Bearbeiten]Octave wurde in Modellierungszyklus 3 genutzt, um die Rückenform zu visualisieren (nachdem dies mit GeoGebra aufgrund der großen Anzahl der Funktionen nicht mehr möglich war). Hierzu wurden Matrizen folgendermaßen in Octave eingegeben: Matrixname=[Einträge der ersten Zeile, mit Komma voneinander getrennt; Einträge der zweiten Zeile, mit Komma voneinander getrennt; ...]. Zeilenvektoren werden als Matrizen mit einer Zeile eingegeben, d.h. in der Form Vektorname=[Einträge des Vektors, mit Komma voneinander getrennt].
Der Befehl "linspace(erster Eintrag, letzter Eintrag, Anzahl Einträge)" gibt einen Zeilenvektor mit der angegebenen Anzahl an Einträgen aus. Hierbei sind der erste und letzte Eintrag die Werte, die im Befehl eingegeben werden. Die restlichen Einträge werden so berechnet, dass das Intervall [erster Eintrag, letzter Eintrag] in gleichgroße Teilintervalle unterteilt wird.
Mit dem Befehl "mesh(x,y,z)" kann ein dreidimensionaler Plot erstellt werden. Die Vektoren x und y stellen hierbei die Skalierung der x- und y-Achse im Plot dar. Die Matrix z gibt die z-Werte an, die den einzelnen Gitterpunkten in der x-y-Ebene zugeordnet sind.
Um Daten aus Octave in eine Tabellenkalkulation zu exportieren, benötigt man das Octave-Paket io. Dazu sind folgende Schritte erforderlich:
- In Octave gelangt man über "Hilfe" - "Octave Pakete" auf die Internetseite octave.sourceforge.io
- Auf der Internetseite gelangt man über "Packages" zu einer Auflistung zahlreicher Pakete. Aus dieser Liste wählt man das Paket "io" und lädt es herunter. Wichtig ist, dass die Datei in dem Ordner gespeichert wird, in dem auch die Dateien gespeichert sind, mit denen man arbeitet.
- Um das Paket zu installieren gibt man in Octave den Befehl "pkg install" gefolgt vom Dateinamen "io-2.6.4.tar.gz" ein.
- Bei jedem Start von Octave muss das Paket mit dem Befehl "pkg load io" geladen werden.
Hat man diese Schritte durchgeführt, kann man Daten aus einer Tabellenkalkulationsdatei in Octave einlesen ("odsread('Dateiname.ods')") oder Daten aus Octave in eine Tabellenkalkulationsdatei exportieren ("odswrite('Wunschname.ods',zu exportierende Variable)"). Das "ods" in diesen Befehlen steht dafür, dass ods-Dateien eingelesen oder erstellt werden. Analog kann man vorgehen für xls-Dateien.
Bezüge zu anderen Modellierungsprojekten
[Bearbeiten]- Kurs:Mathematische Modellbildung/Themen/Radioaktivität und Risikoliteralität, hier wurde ebenfalls Funktionen genutzt die Struktur f(x,y) aufweisen.
Quellen/Literatur
[Bearbeiten]- ↑ UN-Guidelines for Use of SDG logo and the 17 SDG icons (2019/05/10) - https://www.un.org/sustainabledevelopment/news/communications-material/
- ↑ UN-Guidelines for Use of SDG logo and the 17 SDG icons (2019/05/10) - https://www.un.org/sustainabledevelopment/news/communications-material/
- ↑ UN-Guidelines for Use of SDG logo and the 17 SDG icons (2019/05/10) - https://www.un.org/sustainabledevelopment/news/communications-material/
- ↑ Robert Koch Institut: Referenzperzentile für anthropometrische Maßzahlen und Blutdruck aus der Studie zur Gesundheit von Kindern und Jugendlichen in Deutschland (KiGGS). Berlin 2013, S. 20 f. - https://www.rki.de/DE/Content/Gesundheitsmonitoring/Gesundheitsberichterstattung/GBEDownloadsB/referenzperzentile/koerperlaenge.pdf?__blob=publicationFile
- ↑ Robert Koch Institut: Referenzperzentile für anthropometrische Maßzahlen und Blutdruck aus der Studie zur Gesundheit von Kindern und Jugendlichen in Deutschland (KiGGS). Berlin 2013, S. 30 f. - https://www.rki.de/DE/Content/Gesundheitsmonitoring/Gesundheitsberichterstattung/GBEDownloadsB/referenzperzentile/gewicht.pdf?__blob=publicationFile
- ↑ König, Schölmerich, Troje: Geschlechtsspezifische Entwicklung der Anatomie und Gangdynamik im Kindes- und Jugendalter. In: Zeitschrift für Entwicklungspsychologie und Pädagogische Psychologie, 40 (1). Göttingen 2008, S. 35. - https://www.biomotionlab.ca/Text/KonigScholmerich.pdf
- ↑ Prof. Dr. Georg Wydra: Saarbrücker Schulranzenstudie. Erste Ergebnisse. Sportwissenschaftliches Institut der Universität des Saarlandes. - https://www.sportpaedagogik-sb.de/pdf/2009/Wydra%20Potsdam.pdf?r=artikellink
- ↑ Tipler, Paul Allen; Mosca, Gene; Kommer, Christoph (2015): Physik. Für Wissenschaftler und Ingenieure. 7. Aufl. Hg. v. Jennifer Wagner. Berlin: Springer Spektrum. Online verfügbar unter http://dx.doi.org/10.1007/978-3-642-54166-7
- ↑ Joachim Herz Stiftung (o.J.): LEIFIphysik. Online verfügbar unter https://www.leifiphysik.de/mechanik/drehbewegungen/grundwissen/drehmoment
- ↑ https://www.stoffe.de/10-boston-5005_outdoorstoff-wasserdicht-laminiert-blau.html (Stand: 19.12.21)
- ↑ https://www.stoff4you.de/Segeltuchstoffe-Markisenstoffe/Segeltuch-Polyester/Polyester-Stoff-reissfest-und-wasserdicht-Uni.html (Stand: 19.12.21)
- ↑ https://www.novely.de/wasserdichte-stoffe/OXFORD-BIG-Wasserdichter-Outdoorstoff-oxid.html?varselid (Stand: 19.12.21)
- ↑ https://takoy.de/stoff-wasserdichter-polyester-schwarz-ns-1535 (Stand: 19.12.21)
- ↑ https://www.berotex.net/de/kodura-stoff-600d-x-600d-pvc-extra-stark/17847-polyester-stoff-600d600d-pvc-d-a-grade-beschichtet-dunkelblau-058-150-cm-1-lm-5903240231584.html (Stand: 19.12.21)
- ↑ https://www.pure-textilien.de/de_DE/p/Polyester-Oxford-600D-Wasserdicht%2C-Outdoor-Stoff%2C-Segeltuch%2C-Abdeckplane-Schwarz/295 (Stand: 19.12.21)
- ↑ https://www.stoffe-hemmers.de/outdoorstoff-boston-schwarz (Stand: 19.12.21)
- ↑ https://www.extremtextil.de/polyester-pu-beschichtet-b1-flammhemmend-240g-qm-sonderpreis.html (Stand: 19.12.21)
- ↑ https://de.wikipedia.org/wiki/Ebene_(Mathematik)#Schnittpunkt_einer_Geraden_mit_einer_Ebene
- ↑ Bild im Hintergrund: File:Ischial spine - 01 - lateral view.png - https://commons.wikimedia.org/wiki/File:Ischial_spine_-_01_-_lateral_view.png
- ↑ Bild im Hintergrund: File:Ischial spine - 01 - lateral view.png - https://commons.wikimedia.org/wiki/File:Ischial_spine_-_01_-_lateral_view.png
- ↑ Bild im Hintergrund: File:Ischial spine - 01 - lateral view.png - https://commons.wikimedia.org/wiki/File:Ischial_spine_-_01_-_lateral_view.png
- ↑ Bild im Hintergrund: File:Ischial spine - 01 - lateral view.png - https://commons.wikimedia.org/wiki/File:Ischial_spine_-_01_-_lateral_view.png
- ↑ Bild im Hintergrund: File:Ischial spine - 01 - lateral view.png - https://commons.wikimedia.org/wiki/File:Ischial_spine_-_01_-_lateral_view.png
- ↑ https://wiki.geogebra.org/de/Wenn_(Befehl)



























































































































































































![{\displaystyle {\begin{array}{lclcl}p_{f_{1}}&=&\int \limits _{20}^{75}(r_{f1}-f_{1})(x)\;dx&=&\int \limits _{20}^{75}5.0255-(2.7322+2.2932\sin(0.11964x+0.2434))\;dx\\&&&=&\int \limits _{20}^{75}2.2933-2.2932\sin(0.11964x+0.2434)\;dx\\&&&=&{\bigl [}2.2933x+{\frac {2.2932}{0.11964}}\cos(0.11964x+0.2434){\bigr ]}_{20}^{75}\\&&&=&124.15\\p_{f_{2}}&=&\int \limits _{20}^{75}(r_{f2}-f_{2})(x)\;dx&=&\int \limits _{20}^{75}4.8408-(-0.00028754x^{3}+0.042947x^{2}-1.9317x+27.915)\;dx\\&&&=&\int \limits _{20}^{75}0.00028754x^{3}-0.042947x^{2}+1.9317x-23.0742\;dx\\&&&=&{\bigl [}{\frac {0.00028754}{4}}x^{4}-{\frac {0.042947}{3}}x^{3}+{\frac {1.9317}{2}}x^{2}-23.0742x{\bigr ]}_{20}^{75}\\&&&=&115.55\\p_{m_{1}}&=&\int \limits _{20}^{75}(r_{m1}-m_{1})(x)\;dx&=&\int \limits _{20}^{75}5-(2.7+2.3\sin(0.12x+0.228))\;dx\\&&&=&124.4\\p_{m_{2}}&=&\int \limits _{20}^{75}(r_{m1}-m_{1})(x)\;dx&=&\int \limits _{20}^{75}5.627-(-0.00034x^{3}+0.0497x^{2}-2.164x+29.61)\;dx\\&&&=&151.1\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efee657a785f4281c649ccd553f1d600a757f364)









![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce)
![{\displaystyle y\in [c,d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44a51655f18baf55ecb29903da6b8edb9d628646)
![{\displaystyle A=[a,b]\times [c,d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8527ac5bacc1de4253364b08b2bc7beb3010a789)
![{\displaystyle [10,20]\times [0,10]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f6aaa12e74cd1616aa5d3b503a3fd300e6f297c)


![{\displaystyle A=\{(x,y)\in [10,20]\times [0,10]\,|\,y\leq x-10\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec7a1af98768531b858747731390c55f4814e908)
















![{\displaystyle [0,10]\times [0,10]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8716bcea43d106d97a47714db8d41216a96cb42)



![{\displaystyle D_{1}=\{(x,y)^{T}|(x,y)\in [0,10]\times [0,10]\land y\leq -x+10\}=\{(x,y)^{T}|(x,y)\in [0,10]\times [0,10]\land x+y\leq 10\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40402762f1d8978fb89a65cb4afc74b4844f1817)
![{\displaystyle D_{2}=\{(x,y)^{T}|(x,y)\in [0,10]\times [0,10]\land y\geq -x+10\}=\{(x,y)^{T}|(x,y)\in [0,10]\times [0,10]\land x+y\geq 10\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef3470a1585d28b95e1bf821f32d49b1a6f95062)



![{\displaystyle D_{3}=\{(x,y)^{T}|(x,y)\in [10,20]\times [0,10]\land y\leq x-10\}=\{(x,y)^{T}|(x,y)\in [10,20]\times [0,10]\land y-x\leq -10\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78ca0bf0502dabdf8cd1d6aafc719ca82d9e76be)
![{\displaystyle D_{4}=\{(x,y)^{T}|(x,y)\in [10,20]\times [0,10]\land y\geq x-10\}=\{(x,y)^{T}|(x,y)\in [10,20]\times [0,10]\land y-x\geq -10\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b4ee717bb9b1d8af5a6f9501a1828b9ff3410af)






![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)

































































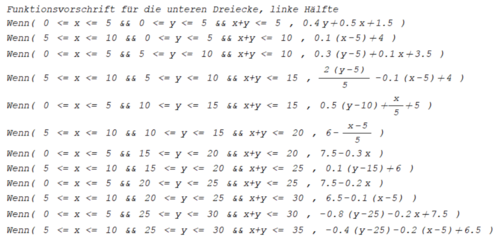














![{\displaystyle Wenn[<Bedingung>,<DannObjekt>]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/910a364bbf43431c0f0395355b69820d243e0e5d)
![{\displaystyle Wenn[<Bedingung>,<DannObjekt>,<SonstObjekt>]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/585198338728a791d021bb00c621d948432d536c)
