Kurs:Mathematische Modellbildung/Themen/Erneuerbare Energien

Modellierungsproblem

Einleitung

Windkraftanlage

Photovoltaikanlage

Im Hinblick auf den Klimawandel ist das Bewusststein für eine nachhaltige Energieproduktion in den letzten Jahren immer weiter in den Vordergrund gerückt. Im Übereinkommen von Paris soll demnach die Energiewende bis zum Jahr 2040 vollständig abgeschlossen sein.

Die Auswirkungen der Klimakrise sind aber schon heute präsent, wie man am Beispiel der Flutkatatrophe 2021 in Nordrhein-Westfalen und Rheinland-Pfalz sehen konnte. Solche Katastrophen werden laut Klimaforschern bedingt durch den Klimawandel deutlich häufiger zu erwarten sein, als noch zu früheren Zeiten.

Besonders betroffen von den Auswirkungen des Klimawandels ist die junge Generation. Im Grunde dessen wurde die Bewegung "Fridays for Future" ins Leben gerufen, wobei vorwiegend Schüler und Schülerinnen auf die Auswirkungen des Klimawandels aufmerksam machen wollen.

Ziel der Modellierung

Im Bezug auf die Dringlichkeit des Handelns bestrebt Deutschland das Ziel bis zum Jahr 2030 den Kohleausstieg zu vollziehen. Zusätzlich werden im Jahr 2022 die letzten Atomkraftwerke abgeschaltet, woraus sich die Frage ergibt, wie Deutschland seine Stromversorgung in den kommenden Jahren aufrecht erhalten kann. Dabei stellen die erneuerbaren Energien eine Lösung zur Aufrechterhaltung des Strombedarfs dar. Wie bekannt ist, sind die meisten erneuerbare Energien jedoch stark von Umwelteinflüssen, wie beispielsweise dem Wetter, abhängig.
Aus diesem Grund stellt das Einsparen von Strom eine zusätzliche Lösung des Problems dar. Strom sparen bedeutet dabei, dass insgesamt weniger Windkrafträder oder ähnliches gebaut werden muss, was zur Nachhaltigkeit beiträgt. Aus diesem Grund ist es überaus wichtig sich der Frage zu stellen, wie gesellschaftlich Strom genutzt wird.

Das vorliegende Modellierungsprojekt setzt sich deshalb mit dem Thema Stromproduktion durch erneuerbare Energien und Stromverbrauch im Haushalt auseinander. Durch das Modellierungsprojekt soll aufgezeigt werden, wo und wann wir im Alltag überall Strom bewusst bzw. unbewusst benötigen. Dabei soll eine Verbindung zur Frage "Wann lässt sich Strom durch erneuerbare Energien überhaupt erzeugen?" hergestellt werden. Das Ziel besteht demnach darin, dass wir Kindern und Jugendlichen bzw. Schüler und Schülerinnen (Fridays for Future) zum nachdenken über den eigenen Stromverbrauch anregen möchten und sich daraus die Fragen nach dem Einsparen von Strom bzw. der Nachhaltigkeit ergeben.

Zielgruppe der Modellbildung

Unser Modellierungsprojekt richtet sich in aller erster Linie an Schüler und Schülerinnen, die bezüglich des eigenen Strombedarfs und der Stromnutzung ihrer Umwelt zum Nachdenken angeregt werden sollen.

Für die heutigen Jugendlichen ist ein Leben ohne Smartphone kaum noch denkbar. Über den Strom, den man zum Aufladen des Smartphones benötigt, machen sich aber kaum die wenigstens Gedanken. Besonders in der heutigen Zeit, in der sich immer mehr Jugendliche für den Klimaschutz einsetzen, ist es deshalb durchaus sinnvoll der betreffenden Zielgruppe ihren Stromkonsum aufzuzeigen und diesen in Verbindung mit der Produktion von Strom durch erneuerbare Energien zu bringen.

Mehrwert der Modellbildung

Der Mehrwert der Modellbildung besteht darin, in aller erster Linie die Umwelt zu erhalten und zu schützen und somit für die "junge" bzw. nächste Generation eine gleichwertige Lebensgrundlage zu schaffen. Eine Stromversorgung durch enereuerbare Energien liefert einen großen Beitrag zur Reduzierung des CO2-Austoßes und damit auch zur Verlangsamung des Klimawandels.
Durch den Ausstieg aus der Kernkraft ist Deutschland auf eine Stromversorgung durch erneuerbare Energien angewiesen. Es ist aber auch wichtig, wie die Gesellschaft mit dem daraus produzierten Strom umgeht. Hierzu bietet das Modellierungsprojekt einen Mehwert, indem aufgezeigt wird, wo und zu welcher Zeit man im eigenen Haushalt am meisten Strom verbraucht. Dieser Vorgang soll ein Grundbewusstsein für einen nachhaltigen Umgang mit Strom schaffen, indem zusätzliche aufgezeigt wird, wann eine Stromproduktion durch erneuerbare Energien überhaupt möglich ist.

Gruppenmitglieder

• Anna Braun
• Jan-Niklas Schwab

Wiki2Reveal

• Einführung (Foliensatz) )
• Rohdaten (Foliensatz)
• Modellierungszyklus 1 (Foliensatz)
• Mathematische Grundlagen Sek I (Foliensatz)
• Implementation Sek I (Foliensatz)
• Implementation Sek I Haushalt 2 (Foliensatz)
• Modellierungszyklus 2 (Foliensatz)
• Mathematische Grundlagen Sek II (Foliensatz)
• Implementation Sek II (Foliensatz)
• Implementation Sek II Haushalt 2 (Foliensatz)
• Modellierungszyklus 3 (Foliensatz)
• Mathematische Grundlagen Uni (Foliensatz)
• Implementation Uni (Foliensatz)

Zuordnung zu Nachhaltigkeitszielen

Sustainable Development Goals

• SDG 7: Affordable an Clean Energy

Die Folgen des Klimawandels sind schon heute global spürbar. Aus diesem Grund ist es das Ziel bis zum Jahr 2030 hauptsächlich auf saubere und erneuerbare Energien zu setzen. Da erneuerbare Energien meist wetterabhängig sind, ist es notwendig im Bezug auf den alltäglichen Strombedarf privater Haushalte, Speichermöglichkeiten bereit zu stellen.

• SDG 13: Climate Action

Die fortschreitende Digitalisierung und die aufkommende E-Mobilität sind unteranderem Gründe für einen steigenden Strombedarf. Erneuerbare Energien sind neben dem bewussten Umgang mit Strom hierbei ein wichtiger Faktor das Klima zu schützen. Bezüglich des bewussten Umgangs mit Strom soll das Modellierungsprojekt den alltäglichen Strombedarf offen darlegen, wodurch Möglichkeiten aufgezeigt werden können, um Strom im Alltag zu sparen.

Daten der Modellbildung

• Rohdaten

Mathematische Theorie für die Modellierungszyklen

• Mathematische Theorie: Sekundarstufe I
• Mathematische Theorie: Sekundarstufe II
• Mathematische Theorie: Uni

Modellierungszyklen

Modellbildungszyklus

In den Modellierungszyklen wird schrittweise

• modelliert,
• bewertet und
• ein Optimierungsvorschlag gemacht,

der in den nächsten Modellierungszyklus einfließt.

Modellierungszyklus 1: Sekundarstufe I

Zielsetzung

In diesem Modellierungszyklus besteht das Ziel darin ...

• ... den Stromverbrauch im eigenen Haushalt über einen ganzen Tag zu bestimmen und diesen mithilfe eines Tabellenkalkulationsprogramms visuell darzustellen.
• ... die Stromproduktion durch erneuerbare Energien am gleichen Tag mithilfe eines Tabellenkalkulationsprogramms darzustellen.
• ... den Verlauf des Strombedarfs mit dem der Stromproduktion zu vergleichen.
• ... die Bilanz zwischen Stromproduktion durch erneuerbare Energien und Stromverbrauch am Tag zu bestimmen.

Vorgehensweise

• Zur Datenerhebung wird die zeitliche Nutzung von Geräten, die mit Strom betrieben werden, stündlich festgehalten. Außerdem wird die Leistung P der benutzen Geräte notiert.
• Die erfassten Daten werden anschließend mithilfe eines Tabellenkalkulationsprogramms in einer Tabelle angelegt.
• Zur Bestimmung des stündlichen Stromverbrauchs (W in Wh) wird die Leistung der Geräte (P in W) mit der Nutzungszeit (t in h) multipliziert

$W=P\cdot t$

und in kWh umgerechnet:

${\frac {W}{1000}}$

• Die hieraus erhaltenen Werte werden mittels eines Tabellenkalkulationsprogramms grafisch dargestellt.

• Für die anschließende Darstellung der Stromproduktion pro Stunde werden die gesammelten Werte in kWh umgerechnet und auf die in Deutschland derzeitigen privaten Haushalte, die sich nach Angaben des statistischen Bundesamts auf aktuell $40,545\cdot 10^{6}$ Haushalte belaufen, hochgerechnet.
• Zum besseren Vergleich werden beide Datenreihen in einer Grafik dargestellt.
• Zur Bestimmung der Stromüber- bzw. Stromunterproduktion durch erneuerbare Energien wird die Fläche unter beiden Liniendiagrammen bestimmt. Die Fläche wird dabei mittels Flächenzerlegung in GeoGebra bestimmt.

Durchführung

• Haushalt 1
• Haushalt 2

Bewertung und Optimierung

Bewertung

• Da nur Messdaten zu vollen Stunden vorliegen, lässt sich der Verlauf zwischen den Daten nur andeuten
• Die hierfür verwendete lineare Interpolation liefert einen konstanten Anstieg bzw. Abstieg zwischen den Daten
• Einen Blick in die Realität lässt aber vermuten, dass dieser lineare Verlauf eher unzutreffend ist
• Grund: Pro Zeiteinheit müsste der Strom um einen konstanten Faktor zunehmen

Optimierung

• Eine genauere Messung kann mithilfe von Strommessern erfolgen
• Sammeln von mehr Messdaten zwischen den vorliegenden Datenpunkten bildet einen genaueren Verlauf ab
• Verlauf zwischen den Messdaten: Kurven (Polynome)
• Dadurch entstehen "weichere" bzw. "glatte" Übergänge zwischen den Datenpunkten
• Es wird keine konstante Steigung mehr angenommen

Modellierungszyklus 2: Sekundarstufe II

Zielsetzung

Im ersten Modellierungszyklus wurde der Verlauf mithilfe eines Liniendiagramms dargestellt. Dies entspricht einer linearen Interpolation. Im 2. Modellierungszyklus werden die Übergänge zwischen den Messpunkten unter Benutzung von Konvexkombinationen interpoliert. Hieraus ergeben sich "weichere" bzw. "glatte" Übergänge zwischen den gesammelten Datenpunkten.

Vorgehensweise

Seien $n\in \mathbb {N}$ Datenpunkte gegeben und $A$ und $B$ seien zwei aufeinanderfolgende Datenpunkte.

Bestimmung der Hilfspunkte (Konvexkombination 2. Ordnung)

Die Ermittlung des Hilfspunkts $S_{1}$ für die Konvexkombinationen 2. Ordnung zwischen $A$ und $B$ erfolgt über die Bestimmung des Schnittpunkts der Tangenten $t_{A}$ und $t_{B}$, die die Punkte $A$ und $B$ berühren.
Es wurde wie folgt vorgegangen:

• Konstruktion der Winkelhalbierenden $w_{A}$ bzgl. des Winkels $\alpha$ mit Scheitelpunkt $A$.
• Konstruktion der Senkrechten $s_{A}$ zur Winkelhalbierenden $w_{A}$.
• Die Senkrechte $s_{A}$ entspricht der gesuchten Tangente $t_{A}$
• Bestimmung der Funktionsgleichung erfolgt über GeoGebra.
• Konstruktion der Winkelhalbierenden $w_{B}$ bzgl. des Winkels $\beta$ mit Scheitelpunkt $B$.
• Konstruktion der Senkrechten $s_{B}$ zur Winkelhalbierenden $w_{B}$.
• Die Senkrechte $s_{B}$ entspricht der gesuchten Tangente $t_{B}$
• Bestimmung der Funktionsgleichung erfolgt über GeoGebra.
• Bestimmung des Schnittpunkts $S_{1}$ zwischen $s_{A}$ und $s_{B}$ liefert den gesuchten Hilfspunkt.

Bestimmung der Hilfspunkte (Konvexkombination 3. Ordnung)

Die Ermittlung der beiden Hilfspunkte $H_{1}$ und $H_{2}$ für die Konvexkombination 3. Ordnung zwischen den Punkten $A$ und $B$ erfolgt über die bereits in Konvexkombination 2. Ordnung bestimmten Tangentengleichungen $t_{A}$ und $t_{B}$ sowie folgender Beziehung bzgl. der $x$ Werte:

$x_{H_{1}}={\frac {2}{3}}\cdot x_{A}+{\frac {1}{3}}\cdot x_{B}$

$x_{H_{2}}={\frac {1}{3}}\cdot x_{A}+{\frac {2}{3}}\cdot x_{B}$

Die zugehörigen $y$ Werte bestimmt man durch einsetzen der errechneten $x$ Werte in die Tangentengleichungen der jeweiligen Punkte $A$ und $B$.

Die Konvexkombination 3. Ordnung wird unteranderem benötigt, falls die beiden Tangenten der beiden Punkte $A$ und $B$ parallel zueinander liegen.

Konstruktion in GeoGeobra

Gegeben seien zwei Punkte $A$ und $B$ zwischen denen eine Konvexkombination 2. Ordnung durchgeführt werden soll. Der Hilfspunkt $S$ wurde dabei wie oben beschrieben bestimmt und $t\in [0,1]$ kann mit Hilfe eines Schiebereglers verändert werden.

1. Konstruiere Punkt $P_{0}$ mit $P_{0}=(1-t)A+tB$
2. Konstruiere Punkt $P_{A}$ mit $P_{A}=(1-t)A+tS$
3. Konstruiere Punkt $P_{B}$ mit $P_{B}=(1-t)S+tB$
4. Konstruiere Punkt $P$ mit $P=(1-t)P_{A}+tP_{B}$
5. Konstruiere die Ortslinie von Punkt $P$

Eine Konvexkombination 3. Ordnung zwischen den Punkten $A$ und $B$ mit den Hilfspunkten $H_{1}$ und $H_{2}$, die sich wie oben beschrieben bestimmen lassen, lässt sich folgendermaßen konstruieren:

1. Konstruiere Punkt $K_{1}$ mit $K_{1}=(1-t)A+tH_{1}$
2. Konstruiere Punkt $K_{2}$ mit $K_{2}=(1-t)H_{1}+tH_{2}$
3. Konstruiere Punkt $K_{3}$ mit $K_{3}=(1-t)H_{2}+tB$
4. Konstruiere Punkt $K_{4}$ mit $K_{4}=(1-t)K_{1}+tK_{2}$
5. Konstruiere Punkt $K_{5}$ mit $K_{5}=(1-t)K_{2}+tK_{3}$
6. Konstruiere Punkt $P$ mit $P=(1-t)K_{4}+tK_{5}$
7. Konstruiere die Ortslinie von Punkt $P$

Durchführung

• Konvexkombination Haushalt 1
• Konvexkombination Haushalt 2

Bewertung und Optimierung

Bewertung

Bei dem modellierten System handelt es sich um ein rein stationäres System, da es sich nur auf Daten bezieht, die an einem bestimmten Tag zu einer festen Uhrzeit aufgenommen wurden. Im Vergleich zum 1. Zyklus, bei dem die "Lücken" zwischen den Daten linear interpoliert wurden, wurden die Zwischenräume zwischen den vorhandenen Daten im 2. Zyklus mittels Konvexkombinationen bis zur 3. Ordnung interpoliert. Hieraus entstehen deutlich "weichere" Übergänge zwischen den Datenpunkten (vgl. Bsp. Federpendel). Hierdurch erhalten wir im Vergleich zum Zyklus 1 eine "differenzierbare" Funktion, die den Stromverbrauch bzw. die Stromproduktion darstellt.

Optimierung

Bezüglich der Darstellung wurde das Modell weitesgehend optimiert. Jedoch wurde schon angedeutet, dass es sich bei dem Modell in Zyklus 1 und Zyklus 2 um ein stationäres System handelt, bei dem sich die Messdaten auf einen bestimmten Zeitraum beziehen. Beim Thema Stromverbrauch und Stromerzeugung handelt es sich jedoch eher um dynamische Prozesse. Elektronische Geräte werden immer Stromsparender aber zugleich wird mehr Strom durch eine aufkommende E-Mobilität und Digitalisierung benötigt. Neben diesen Aspekten muss aber auch die Wetterabhängigkeit bzw. Zeitabhängigkeit (Jahreszeit) berücksichtigt werden. Im Winter gibt es nämlich weniger Sonnenstunden als im Sommer. Für uns bedeutet das, dass wir im Winter wahrscheinlich mehr Strom benötigen, jedoch kann nicht so viel Strom durch Solarpanels wie im Sommer erzeugt werden. Aber auch globale Situationen, wie die Corona Pandemie, besitzen eine Auswirkung auf den Stromverbrauch (z.Bsp. Homeoffice).
Wie man also sieht ist der Stromverbrauch und die Stromerzeugung ein dynamischer Prozess, wodurch es sinvoll wäre ein dynamisches Modell zu entwickeln, welches neue Daten in das bestehende System integrieren kann und somit immer aktuell gehalten wird.

Modellierungszyklus 3: Uni-Niveau

Zielsetzung

Im ersten Modellierungszyklus wurde der Verlauf mithilfe eines Liniendiagramms dargestellt. Dies entspricht einer linearen Interpolation. Im zweiten Modellierungszyklus wurden die Übergänge zwischen den Messpunkten unter Benutzung von Konvexkombinationen interpoliert.
Im 3. Zyklus soll es um die Frage gehen, wie sich neue Messdaten auf den bisherigen Verlauf des Stromverbrauchs auswirken. Es wird daher ein dynamisches und adaptives Modell entwickelt. Hierfür wird als mathematisches Hilfsmittel das Gradientenabstiegsverfahren verwendet, welches die Abweichung zwischen den bisherigen Daten und den neuen Daten minimieren soll, wodurch sich ein aktualisierter Kurvenverlauf ergibt.

Vorgehensweise

Die Grundlage für ein dynamisches System bilden neue Daten $D$, die z.Bsp. in einem Tabellenkalkulationsprogramm gesammelt werden können.
In diesem Zyklus beschränken wir uns dabei zuerst auf ein bestimmtes Zeitintervall zwischen zwei bestehenden Stützstellen. Hierfür verwendet wir den Zeitraum zwischen 7 Uhr und 8 Uhr. Für dieses Intervall werden $n\in \mathbb {N}$ neue Daten $D$ gesammelt.

$D=\left\{\left({\tilde {x}}_{1},{\tilde {y}}_{1}\right),...,\left({\tilde {x}}_{n},{\tilde {y}}_{n}\right)\right\}$

Mittels einer linearen Regression möchten wir die direkte Verbindungsstrecke zwischen den bestehenden Stützstellen $(x_{1}|y_{1})$ und $(x_{2}|y_{2})$ so verändern, dass die Abweichung zwischen der Geraden und den neuen Daten minimiert wird.
Hierzu betrachten wir die Fehlerfunktion

$E(x_{1},x_{2},y_{1},y_{2})={\frac {1}{n}}\sum _{k=1}^{n}(f({\tilde {x}}_{k})-{\tilde {y}}_{k})^{2}$

Dies entspricht der mittleren quadratischen Abweichung zwischen den neuen Daten und den bisherigen Daten. Da die Visualisierung anschließend in GeoGebra umgesetzt werden soll, sind wir daran interessiert wohin sich die bisherigen Stützstellen $(x_{1}|y_{1})$ und $(x_{2}|y_{2})$ verschieben, sodass die mittlere quadratische Abweichung minimiert wird.
Hierzu stellen wir die Gerade zwischen den Stützstellen als Konvexkombination 1. Ordnung dar. Hierzu betrachtet man im $\mathbb {R} ^{2}$ nur die y-Komponente. Es gilt:

$f(t)=(1-t)\cdot y_{1}+t\cdot y_{2}$ mit $t\in [0,1]$

$t$ kann nun mithilfe der Strahlensätze folgendermaßen dargestellt werden:

$t={\frac {x-x_{1}}{x_{2}-x_{1}}}$

Zwischen den Stützpunkten $(x_{1}|y_{1})$ und $(x_{2}|y_{2})$ ergibt sich somit folgende Funktionsgleichung:

$f(x)={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}\cdot x+{\frac {x_{2}y_{1}-x_{1}y_{2}}{x_{2}-x_{1}}}$

Mit dieser Funktionsgleichung lautet unsere Fehlerfunktion nun:

$E(x_{1},x_{2},y_{1},y_{2})={\frac {1}{n}}\sum _{k=1}^{n}({\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}\cdot {\tilde {x}}_{k}+{\frac {x_{2}y_{1}-x_{1}y_{2}}{x_{2}-x_{1}}}-{\tilde {y}}_{k})^{2}$

Das Ziel ist es nun den obigen Fehler zu minimieren. Hierfür verwendet wir das Gradientenabstiegsverfahren, welches in Octave umgesetzt wird. Da unsere Fehlerfunktion von $x_{1}$, $x_{2}$, $y_{1}$, $y_{2}$ abhängt müssen wir diese vier mal partiell ableiten um unseren Gradienten zu erhalten. Die partiellen Ableitungen wurden mithilfe von WxMaxima berechnet. Diese lauten:

${\frac {\partial E}{\partial x_{1}}}={\frac {2}{n}}\sum _{k=1}^{n}(-{\frac {x_{2}y_{1}-x_{1}y_{2}}{(x_{2}-x_{1})^{2}}}-{\tilde {x}}_{k}\cdot {\frac {y_{2}-y_{1}}{(x_{2}-x_{1})^{2}}}+{\frac {y_{2}}{x_{2}-x_{1}}})\cdot ({\tilde {y}}_{k}-({\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}\cdot {\tilde {x}}_{k}+{\frac {x_{2}y_{1}-x_{1}y_{2}}{x_{2}-x_{1}}}))$

${\frac {\partial E}{\partial x_{2}}}={\frac {2}{n}}\sum _{k=1}^{n}({\frac {x_{2}y_{1}-x_{1}y_{2}}{(x_{2}-x_{1})^{2}}}+{\tilde {x}}_{k}\cdot {\frac {y_{2}-y_{1}}{(x_{2}-x_{1})^{2}}}-{\frac {y_{1}}{x_{2}-x_{1}}})\cdot ({\tilde {y}}_{k}-({\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}\cdot {\tilde {x}}_{k}+{\frac {x_{2}y_{1}-x_{1}y_{2}}{x_{2}-x_{1}}}))$

${\frac {\partial E}{\partial y_{1}}}={\frac {2}{n}}\sum _{k=1}^{n}({\frac {{\tilde {x}}_{k}}{x_{2}-x_{1}}}-{\frac {x_{2}}{x_{2}-x_{1}}})\cdot ({\tilde {y}}_{k}-({\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}\cdot {\tilde {x}}_{k}+{\frac {x_{2}y_{1}-x_{1}y_{2}}{x_{2}-x_{1}}}))$

${\frac {\partial E}{\partial y_{2}}}={\frac {2}{n}}\sum _{k=1}^{n}({\frac {x_{1}}{x_{2}-x_{1}}}-{\frac {{\tilde {x}}_{k}}{x_{2}-x_{1}}})\cdot ({\tilde {y}}_{k}-({\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}\cdot {\tilde {x}}_{k}+{\frac {x_{2}y_{1}-x_{1}y_{2}}{x_{2}-x_{1}}}))$

Die Richtung des Gradienten zeigt immer in Richtung des steilsten Anstiegs. Da wir jedoch unseren Fehler minimieren möchten, bilden wir den negativen Gradienten. Unter Benutzung des negativen Gradienten berechnen wir in Octave nun die neuen Werte bzgl. $x_{1}$, $x_{2}$, $y_{1}$ und $y_{2}$ wie folgt:

$x_{1neu}=x_{1}-L\cdot {\frac {\partial E}{\partial x_{1}}}(x_{1})$

$x_{2neu}=x_{2}-L\cdot {\frac {\partial E}{\partial x_{2}}}(x_{2})$

$y_{1neu}=y_{1}-L\cdot {\frac {\partial E}{\partial y_{1}}}(y_{1})$

$y_{2neu}=y_{2}-L\cdot {\frac {\partial E}{\partial y_{2}}}(y_{2})$

Hierbei ist L die sogenannte Schrittweite, die angibt, wie schnell wir uns dem Minimum annähern. Bei der Wahl der Schrittweite muss darauf geachtet werden, dass diese nicht zu groß ist, denn sonst besteht die Gefahr, dass das Gradientenabstiegsverfahren divergiert.
Hat die Fehlerfunktion $E(x_{1},x_{2},y_{1},y_{2})$ einen minimalen Wert angenommen, so haben wir die neuen Werte bzgl. $x_{1}$, $x_{2}$, $y_{1}$ und $y_{2}$ gefunden.
Zur Visualisierung können die Stützstellen zu Begin nun auf die neuen Koordinaten verschoben werden.

Durchführung

Neue und aktuellere Daten $D$ werden mithilfe eines Tabellenkalkulationsprogramms gesammelt. Aus zeitlichen Gründen haben wir fiktive Daten zur Implementierung unseres Modells in Octave genutzt. Diese können jedoch beliebig bearbeitet werden.

Folgender Code wurde in Octave zur Durchführung des Gradientenabstiegsverfahrens genutzt:

Zu Begin des Programms werden die in Excel eingetragenen Daten als Matrix $D$ in Octave eingelesen. Dies geschieht mit dem Befehl xlsread(' Datei ',' Anfang:Ende '). Die x-Werte bzw. die y-Werte der neuen Datenpunkte werden anschließend als Vektoren $X$ und $Y$ aufgefasst.
Als Startwert für das Gradientenabstiegsverfahren wurden die Stützstellen $x_{1}$, $x_{2}$, $y_{1}$ und $y_{2}$ gewählt. Die Schrittweite L muss je nach Daten manuell eingestellt werden. Hierbei gilt es zu beachten, je geringer die Schrittweite L ist, desto mehr Iterationsschritte werden benötigt, was eine hohe Rechenleistung beansprucht. Aber zugleich gilt, je größer die Schrittweite ist, desto höher ist das Risiko das Minimum zu "überspringen".
Der Kern der Implementierung besteht aus einer for-Schleife, die bis zu dem angegebenen Iterationsschritt durchgeführt wird. Hier werden die Startwerte für $x_{1}$, $x_{2}$, $y_{1}$ und $y_{2}$ in die entsprechenden partiellen Ableitungen eingesetzt. Der erhaltene Wert wird mit der angegebenen Schrittweite L multipliziert und vom entsprechenden Startwert abgezogen. Dieser Vorgang wird solange wiederholt, bis die angegebene Schrittzahl erreicht ist.
Zur besseren Einschätzung der Minimierung wird neben den neuen Werten für $x_{1}$, $x_{2}$, $y_{1}$ und $y_{2}$ auch der noch vorhandene Fehler ausgegeben.
Durch Implementation der neuen Daten erhalten wir folgende Koordinaten für unsere neuen Stützstellen:

Diese Werte ergaben sich bei einer Schrittweite von $L=0.001$ und $100000$ Iterationsschritten. Eine weitere Minimierung des Fehlers war durch Veränderung der Schrittweite L, sowie der Anzahl der Iterationsschritten nicht gegeben.
Die Visualisierung des neues Verlaufs erfolgt nun in GeoGebra.

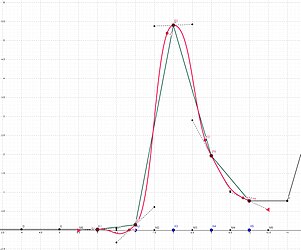
• Veränderung des Verlaufs zwischen 7 Uhr und 8 Uhr
• 
  Verlauf vor der Durchführung des Gradientenabstiegsverfahrens
• 
  Verlauf nach der Durchführung des Gradientenabstiegsverfahrens

Durch die neuen aktuelleren Daten hat sich der Verlauf bzgl. des Stromverbrauchs in negative x-Richtung verschoben.

Bewertung und Optimierung

Bewertung

In der obigen Implementation wurden neue Daten zwischen den Stützstellen miteinbezogen. Dadurch wird für die Messung der neuen Daten kein fester Zeitpunkt vorgegeben, wodurch neue Messungen zu beliebigen Zeitpunkten möglich ist.
Ledeglich beschränkten wir uns auf ein bestimmtes Zeitintervall, in der die Messung stattfindet. Mittels der durchgeführten linearen Regression erhalten wir die neue Position der Stützstellen, zwischen denen man neue Daten implementiert. In einer dynamischen GeoGebra Datei bzgl. der Konvexkombination 3. Ordnung können die erhaltenen Stützstellen angepasst werden. die Konvexkombination 3. Ordnung bleibt trotz der Verschiebung erhalten. So ergibt sich insgesamt ein veränderter Verlauf bzgl. der Stromverbrauchskurve.

Optimierung

Die nächste Optimierungsstufe würde den Einbezug weiterer Intervalle (vorzugsweise der Nachbarintervalle) beinhalten. Dies bedeuetet, dass noch mehr neue Daten eingebettet und ausgewertet werden können.
Zudem können wir von einer linearen Regression zu einer nicht-linearen Regression (kubisch) übergehen, wodurch der Fehler zwischen der Ortslinie der Konvexkombination 3. Ordnung und den neuen Daten weitesgehend minimiert werden kann.

Software

Tabellenkalkulation (Excel)

Tabellenkalkulationsprogramme wie Libre Office Calc oder Excel werden vor allem für Wirtschaftsprognosen, Kostenkalkulationen und deren visuelle Präsentation genutzt.
Im Mathematikunterricht kann die Tabellenkalkulation unteranderem für die Erstellung von Wertetabellen und Diagrammen, die Implementation von numerischen Verfahren, wie z.Bsp. dem Heron-Verfahren oder der Newton-Iteration oder für einfache Berechnungen genutzt werden. Aber auch für stochastische Experimente kann die Software genutzt werden, wie beispielsweise das Erzeugen von Zufallszahlen oder das Berechnen des Binomialkoeffiezienten.
In Zyklus 1 haben wir uns für den Einsatz des Tabellenkalkulationsprogranmms Excel entschieden. Das Ziel war es den Stromverbrauch bzw. die Stromproduktion an einem Tag zu bestimmen und den Verlauf der gesammelten Datenpunkte visuell darzustellen. Die gesammelten Messwerte wurden dabei in einer Wertetabelle festgehalten. Diese konnten mithilfe der integrierten Summenfunktion SUMME(Zahl1,Zahl2,...) recht einfach zusammengerechnet werden, wodurch sich unsere Datenpunkte ergaben. Diese wurden anschließend mithilfe der Diagramm-Funktion in einem Liniendiagramm dargestellt.

GeoGebra

Bei GeoGebra handelt es sich um ein dynamisches Mathematiksystem, welches geometrische und algebraische Anwendungen anbietet. Neben diesen zwei Hauptanwendungen ist zudem eine Tabellenkalkulation enthalten. Da hierbei wesentliche Themenbereiche des Schulstoffs abgedeckt werden, eignet sich GeoGebra auch sehr gut für den Einsatz im Mathematikunterricht. Das relativ einfache Interface bietet zudem einen einfachen Einstieg in die Software, was für Schüler und Schülerinnen wichtig ist. Zudem können mithilfe von Geogebra auch Unterrichtsmaterialien erstellt werden, wie virtuelle Arbeitsblätter.
GeoGebra wurde bei unserer Modellierung in allen drei Zyklen verwendet, wobei sich der Schwerpunkt in Zyklus 2 befindet. In Zyklus 1 wurde die Software zur Berechnung von Flächeninhalten benutzt (geometrische Anwendung). Das Ziel war es die Fläche unter dem "Liniendiagramm" zu ermitteln. In einer Tabellenkalkulation wäre dies im Vergleich zu GeoGebra deutlich aufwendiger gewesen, denn eine direkte Flächenbestimmung ist hier nicht möglich. Anders in GeoGebra. Hier konnte man den Graph in 23 Trapeze unterteilen. Für diese Unterteilung wurde das Tool n-Eck genutzt. Die Eckpunkte der jeweiligen Trapeze wurden durch anklicken ausgewählt. Wurde der Anfangspunkt wieder erreicht, so erfasst GeoGebra die Fläche als n-Eck und gibt gleichzeitig den Flächeninhalt an.
In Zyklus 2 wurde die Software genutzt um Konvexkombinationen zu erzeugen. Für Konvexkombinationen 2. und 3. Ordnung benötigt man einem bzw. zwei Hilfspunkte. Diese lassen sich mithilfe der Winkelhalbierenden und der dazu stehenden Senkrechen bestimmen. Mittels des Befehls Winkelhalbierende('PunktA','PunktB','PunktC') und dem Befehl Senkrechte('PunktB','Winkelhalbierende') konnte die Tangente zum Punkt B bestimmt werden. Die Funktionsgleichung dieser wird automatisch von GeoGebra ausgegeben. Mithilfe dieser kann man durch Einsetzen des x-Werts den y-Wert der Hilfspunkte bzgl. der Konvexkombination 3. Ordnung bestimmen. Der Schnittpunkt zweier benachbarter Tangenten der dem Hilfspunkt bei einer Konvexkombination 2. Ordnung entspricht, wurde mithilfe des Befehls Schnittpunkt('Gerade1','Gerade2') ermittelt. Zur anschließenden Konstruktion der Konvexkombinationen wurde das Eingabefenster benutzt. Durch die Möglichkeit der Erstellung eines Schiebreglers können Parameter (hier: t) unterschiedliche Werte durchlaufen. Mithilfe dieser Methode war es möglich die Ortskurve eines Punktes darzustellen. Diese diente im 2. Zyklus als Visualisierung.
In Zyklus 3 wurde GeoGebra widerum zur Visualisierung eines dynamischen System benutzt. Durch die Möglichkeit Punkte frei zu bewegen bzw. Abhängigkeiten zwischen Punkten und Geraden festzulegen hat sich die Software hierfür angeboten.

GNUOctave

Bei Octave handelt es sich um eine Programmiersprache, die hauptsächlich für numerische Lösungen mathematischer Aufgaben und für vektorisierbare Berechnungen verwendet wird. Im Vergleich zu anderen Programmen bietet Octave eine graphische Benutzeroberfläche. Zudem ist die Software weitestgehend mit der kostenpflichtigen Software Matlab kompatibel, wodurch eine Vernetzung zwischen beiden Systemen möglich ist. Octave ist vorallem sinvoll, wenn man sich mit der Verarbeitung von Daten beschäftigt.
In Octave gibt es ein sogeganntes "Befehlsfenster". Dieses ermöglicht eine Zeileneingabe z.Bsp. für den Abruf einer Funktion oder einer Berechnung. Vergleichbar ist dies mit einem Taschenrechner. Zusätzlich gibt es die Möglichkeit "Skripts" zu schreiben. Hierzu muss man zum Fenster "Editor" wechseln. Neben den in Octave enthaltenen Funktionen können hier auch eigene Funktionen erstellt werden, die im Befehlsfenster abrufbar sind.
In Zyklus 3 wurde das Gradientenabstiegsverfahren in Octave implementiert. Die Basis unseres Modells im 3. Zyklus bilden neue Daten, die keinerlei begrenzt sind. Octave bietet z.Bsp. die Möglichkeit Daten im .csv Format aber auch im .xlsx zu importieren. Für den Import letzterer Datei benötigt man jedoch ein Zusatzpaket, welches sich auf GNUOctave herunterladen lässt. Durch diese einfache Möglichkeit Daten zu importieren erachteten wir Octave als sinvolles Hilfsmittel zur Umsetzung unseres Modells. Zudem ermöglichte uns Octave das durchzuführende Iterationsverfahren mit wenigen Eingaben umzusetzen. Zur Umsetzung wurde ein Skript angelegt, bei dem hauptsächlich eine for-Schleife umgesetzt wurde.