Kurs:Analysis (Osnabrück 2013-2015)/Teil III/Vorlesung 75
- Das Konzept einer Mannigfaltigkeit
In der zweiten Hälfte dieses Kurses werden wir den Begriff der Mannigfaltigkeit entwickeln. Als Beispiel betrachten wir die Erde (ihre Oberfläche), die in der Wissenschaftsgeschichte lange für eine Scheibe gehalten wurde, und zwar aus gutem Grund. Sie sieht nämlich lokal aus wie eine Ebene. Dies spiegelt sich auch in den Karten wider, die man sich von ihr macht. Eine Karte ist ein ebenes „Blatt“, dessen Punkte in Bijektion zu einem Ausschnitt der Erdoberfläche steht. Insbesondere bei kleinen Ausschnitten halten wir das für unproblematisch, bei Karten aber, die große Ausschnitte oder gar die gesamte Erde wiedergeben sollen, tauchen schnell Fragen auf, was die Karte richtig wiedergibt und was nicht, Fragen nach der Längentreue, Flächentreue, Winkeltreue, Fragen über fehlende Punkte oder mehrfach auftretende Punkte, Fortsetzungsfragen, Krümmungsfragen ...
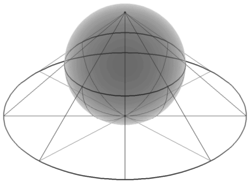
Wir besprechen zunächst die stereographische Projektion der Kugeloberfläche.
Wir betrachten die Kugeloberfläche
und nennen den Punkt Nordpol und den Punkt Südpol. Ein Punkt , , definiert zusammen mit dem Nordpol eine eindeutige Gerade im Raum, die durch
parametrisiert ist. Der Vektor , der diese Gerade definiert, ist nicht parallel zur -Ebene, d.h. dass es genau einen Schnittpunkt dieser Geraden mit dieser Ebene gibt. Dieser ergibt sich zum Parameter
es handelt sich um den Punkt
Wir fassen diese Konstruktion als eine Abbildung
auf. Es ist anschaulich klar, dass diese Abbildung eine Bijektion ist, was sich auch einfach über die Formeln nachrechnen lässt. Die Umkehrabbildung ergibt sich, indem man einen Punkt der Ebene mit dem Nordpol verbindet und den Durchstoßungspunkt mit der Kugeloberfläche berechnet. Dies führt zur Bedingung
was auf
führt. Die Lösung entspricht dem Nordpol, an der wir nicht interessiert sind, sodass wir auf geführt werden, also auf die Abbildung
Insbesondere ist also die reelle Ebene homöomorph zur in einem Punkt „gelochten“ Kugeloberfläche.
Eine entsprechende Überlegung kann man für anstellen. Dies führt zur Abbildung
mit der Umkehrabbildung
Der Südpol entspricht bei der ersten Abbildung dem Mittelpunkt der euklidischen Ebene und der Nordpol entspricht bei der zweiten Abbildung dem Mittelpunkt der euklidischen Ebene. Wir nennen beide Abbildungen bzw. ihre Umkehrabbildungen Karten. Beide Karten decken zusammen die gesamte Kugeloberfläche ab. Da es sich um Homöomorphismen handelt, geben sie die wesentlichen topologischen Eigenschaften der Sphäre richtig wieder. Sie sind beide nicht für die Geographie der Erde gut geeignet, da die Karten die gesamte Ebene benötigen und die Längen sehr stark verzerren.
Beide Karten sind gleich gut. Es ist einfach, Punkte (und allgemeiner andere Figuren) auf der einen Karte in die andere Karte umzurechnen. Man muss dabei allerdings beachten, dass die beiden Pole nur in einer Karte vertreten sind. Die Punkte der Menge finden sich auf beiden Karten, und zwar stehen sie durch beide Karten in Bijektion zu der im Mittelpunkt gelochten Ebene . Die Übergangsabbildung (oder der Kartenwechsel) wird durch gegeben. Dabei ist
Diese Übergangsabbildung induziert nicht nur einen Homöomorphismus zwischen mit ,[1] was unmittelbar daraus folgt, dass die Kartenabbildungen und Homöomorphismen sind, sondern sogar einen Diffeomorphismus. Dies ist direkt aus der Funktionsvorschrift ablesbar; es macht aber keinen Sinn zu sagen, dass die Kartenabbildungen Diffeomorphismen sind, da ja die Kugeloberfläche keine offene Teilmenge im ist. Was bisher fehlt ist eine „differenzierbare Struktur“ auf dieser Oberfläche, um von diffeomorph sprechen zu können.
Eine Mannigfaltigkeit ist ein geometrisches Gebilde, das „lokal“ so aussieht wie der euklidische Raum . Dabei setzen wir dieses geometrische Gebilde als einen topologischen Raum an, und lokal wird dadurch präzisiert, dass es eine Überdeckung aus offenen Mengen gibt, die homöomorph zu offenen Teilmengen des sind. Obwohl wir im Folgenden mit topologischen Räumen arbeiten sei erwähnt, dass sich der Vorstellungsgehalt des Folgenden nicht verringert, wenn man bei einem topologischen Raum einfach an einen metrischen Raum denkt.
- Differenzierbare Mannigfaltigkeiten
Ein topologischer Hausdorff-Raum heißt eine topologische Mannigfaltigkeit der Dimension , wenn es eine offene Überdeckung derart gibt, dass jedes homöomorph zu einer offenen Teilmenge des ist.
Zu jedem Punkt gibt es also eine offene Umgebung , die homöomorph zu einer offenen Teilmenge ist. Sei
eine Homöomorphie und sei . Dann entspricht einer offenen Ballumgebung eine offene Umgebung mit , die nach Konstruktion homöomorph zu einem offenen Ball ist. Man kann daher eine topologische Mannigfaltigkeit auch als einen topologischen Hausdorff-Raum charakterisieren, der lokal euklidisch ist.
Es sei eine topologische Mannigfaltigkeit. Dann nennt man jede Homöomorphie
wobei und offen sind, eine (topologische) Karte für .
Dabei nennt man die offene Menge manchmal das Kartengebiet und das Kartenbild. Zu einer Karte
und einer offenen Teilmenge ist auch die induzierte Abbildung
eine Karte. Manchmal nennt man auch die Umkehrabbildung eine Karte. Statt Karte spricht man auch von einem lokalen Koordinatensystem. Durch die Karte werden ja die Koordinaten auf auf übertragen. Die -te Koordinate (die -te Projektion) induziert die (lokale Koordinaten)-Funktion
(die oft einfach wieder mit bezeichnet wird), und ein Punkt entspricht einem Punkt .
Es sei eine topologische Mannigfaltigkeit, es seien offene Teilmengen und und seien Karten (mit offen). Dann heißt die Abbildung
Der Durchschnitt ist die offene Teilmenge, auf der beide Karten definiert sind und worauf man die beiden Karten vergleichen kann. Genauer müsste man in der Definition von der Einschränkung von auf die offene Teilmenge sprechen.
Es seien und . Ein topologischer Hausdorff-Raum zusammen mit einer offenen Überdeckung und Karten
mit offen derart, dass die Übergangsabbildungen
- Diffeomorphismen für alle sind, heißt -Mannigfaltigkeit oder differenzierbare Mannigfaltigkeit (der Dimension vom Differenzierbarkeitsgrad ). Die Menge der Karten , , nennt man auch den -Atlas der Mannigfaltigkeit.
Eine differenzierbare Mannigfaltigkeit ist insbesondere eine topologische Mannigfaltigkeit. Nach unserer Definition ist der Atlas ein integraler Bestandteil des Mannigfaltigkeitsbegriffs. Wichtiger als der Atlas ist aber die durch den Atlas definierte differenzierbare Struktur auf der Mannigfaltigkeit. Dies wird deutlicher, wenn wir den Begriff der differenzierbaren Abbildung zwischen zwei Mannigfaltigkeiten zur Verfügung haben und von diffeomorphen Mannigfaltigkeiten sprechen können.
Es sei eine differenzierbare Mannigfaltigkeit. Eine offene Teilmenge , die mit den eingeschränkten Karten versehen ist, heißt offene Untermannigfaltigkeit.
Jede offene Teilmenge ist eine - Mannigfaltigkeit, wenn man die Identität als Karte nimmt. Die einzige Übergangsabbildung ist dann ebenfalls diese Identität, die ein -Diffeomorphismus ist. Dies ist dann eine Mannigfaltigkeit mit einem Atlas, der aus einer einzigen Karte besteht. Man kann aber genauso gut den Atlas nehmen, der aus sämtlichen offenen Teilmengen und den zugehörigen identischen Karten besteht. Die Übergangsabbildungen sind dann die Identitäten auf .
Wir haben schon früher im Kontext des Zwischenwertsatzes von zusammenhängenden metrischen Räumen gesprochen. Die gleiche Definition verwenden wir auch für topologische Räume.
Ein topologischer Raum heißt zusammenhängend, wenn es in genau zwei Teilmengen gibt (nämlich und der Gesamtraum ), die sowohl offen als auch abgeschlossen sind.
Häufig interessiert man sich nur für zusammenhängende Mannigfaltigkeiten, vor allem deshalb, da man im nicht zusammenhängenden Fall die einzelnen „Zusammenhangskomponenten“ getrennt voneinander untersuchen kann. Wir besprechen kurz niedrigdimensionale Mannigfaltigkeiten.
Bei einer nulldimensionalen Mannigfaltigkeit gibt es für jeden Punkt eine offene Umgebung , die homöomorph zu einer offenen Menge des ist. D.h. dass die einpunktige Menge offen sein muss, und daher muss die diskrete Topologie tragen, d.h. jede Teilmenge ist offen. Daher ist die einzige zusammenhängende nulldimensionale Mannigfaltigkeit die einpunktige Menge.
An eindimensionalen Mannigfaltigkeiten gibt es zunächst die offenen Teilmengen des . Diese sind Vereinigungen von offenen Intervallen, und sie sind genau dann zusammenhängend, wenn sie ein offenes Intervall sind. Jedes offene, beschränkte oder unbeschränkte Intervall ist homöomoph und auch diffeomorph zum offenen Einheitsintervall und zu den reellen Zahlen selbst. Die abgschlossenen Intervalle mit sind keine Mannigfaltigkeiten, da es für die Randpunkte (die Intervallgrenzen) keine offene Umgebung gibt, die homöomorph zu einem offenen Intervall ist (sie sind aber sogenannte Mannigfaltigkeiten mit Rand).
Darüber hinaus gibt es noch den Kreis (die Sphäre) als weitere zusammenhängende eindimensionale Mannigfaltigkeit. Es ist
Für jeden Punkt ist homöomorph zu (durch stereographische Projektion). Der Kreis ist nicht homöomorph zu , da der Kreis kompakt[2] ist, die reellen Zahlen aber nicht. Neben und gibt es keine weiteren eindimensionalen zusammenhängenden Mannigfaltigkeiten mit abzählbarer Basis der Topologie (was hier ohne Beweis erwähnt sei).
Ab der Dimension zwei ist es ohne starke zusätzliche Voraussetzungen nicht möglich, sich eine Übersicht über alle Mannigfaltigkeiten zu verschaffen.
- Fußnoten
- ↑ Es empfiehlt sich hier nicht, „mit sich“ zu sagen, da man sich die beiden Kartenebenen als unabhängig voneinander vorstellen sollte. Die Beziehung zwischen ihnen entsteht allein dadurch, dass sie beide die gleiche Kugeloberfläche beschreiben.
- ↑ Allerdings haben wir den Kompaktheitsbegriff bisher nur für Teilmengen im definiert; wir werden bald sehen, dass es sich um einen absoluten Begriff handelt, der nicht von der Einbettung abhängt. Man kann also nicht irgendwie in den homöomorph einbetten, so dass das Bild kompakt ist.
| << | Kurs:Analysis (Osnabrück 2013-2015)/Teil III | >> |
|---|





















































































![{\displaystyle {}]0,1[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e10240bd775389df50353c3fe6e4543873c2ba3)

![{\displaystyle {}[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e5a6e660b5cdc1a9c76f6e6b0d486328c3f6937)




