Kurs:Analysis (Osnabrück 2021-2023)/Teil I/Vorlesung 28
- Gewöhnliche Differentialgleichungen
Wir beginnen mit zwei Beispielen, die beide zu gewöhnlichen Differentialgleichungen führen.
Wir versuchen, die Ausbreitung einer Virusinfektion wie bei den Wellen der Corona-Pandemie seit 2020 zu modellieren. Die Ausbreitung wird durch eine Funktion
beschrieben, wobei für die Zeit und für die Gesamtanzahl der bis zum Zeitpunkt Infizierten (einschließlich der Genesenen) angibt. Dies ist zunächst eine empirische Funktion, die man aus verschiedenen Gründen auch gar nicht genau kennt, insbesondere, da nicht jeder getestet wird. Man kann stattdessen auch die Entwicklung der bestätigt Infizierten betrachten. Diese empirische Funktion wird durch die Daten, die jeden Tag das Robert-Koch-Institut übermittelt, beschrieben, und ist so gesehen zunächst eine Abbildung von einer Anfangsmenge der natürlichen Zahlen (die ersten Tage seit Ausbruch) in die natürlichen Zahlen, wobei jedem Tag die Anzahl der bis dahin Infizierten zugeordnet wird.
Wenn man zu den Daten aus verschiedenen Ländern (oder verschiedenen Wellen) den Verlauf skizziert, ergibt sich jeweils ein ähnliches Bild. Die Ausbreitung scheint einer Gesetzmäßigkeit zu folgen, die man in der mathematischen Modellierung verstehen möchte. Das bedeutet (in einem ersten Schritt), dass man die empirische Funktion, also das vorliegende Datenmaterial, durch eine mathematische Funktion, also einen funktionalen Ausdruck, annähern möchte, um so den qualitativen und den quantitativen Verlauf der Ausbreitung zu verstehen und auch Extrapolationen (Prognosen) formulieren zu können. Hierbei wird man den Definitionsbereich und den Wertebereich als die reellen Zahlen (oder Intervalle davon) und die Funktion als stetig oder differenzierbar ansetzen. Man kann mit verschiedenen Zeiteinheiten arbeiten und auch die Gesamtzahl absolut oder aber prozentual (bezogen auf die Erdbevölkerung, ein Land, ...) angeben. So oder so ergibt sich, dass der Verlauf gut durch eine Exponentialfunktion beschrieben werden kann, also von der Bauart
mit einer Basis ist. Welche Basis zu nehmen ist, hängt von der Skalierung und auch von länderspezifischen Gegebenheiten ab. Diese Basis ist äquivalent zum Verdoppelungszeitraum der Ausbreitung, man kann das eine aus dem andern berechnen, siehe Aufgabe 28.2.
Diese Modellierung ist bisher aber nur die Beobachtung einer Übereinstimmung einer mathematischen Funktionsklasse mit empirischen Funktionen. In einem zweiten Schritt kann man sich fragen, ob es „in der Natur der Sache liegt“, dass die Ausbreitung eines Virus exponentiell verläuft. Gibt es einen mathematischen Grund dafür, eine innere Dynamik, eine zu jedem Zeitpunkt gültige Gesetzmäßigkeit, die den Verlauf erklären kann? Die Antwort zu dieser Frage erfolgt im Rahmen der Theorie der gewöhnlichen Differentialgleichungen, und beruht auf einer einfachen Beobachtung. Wir nehmen die Funktion als differenzierbar an. Die Ableitung beschreibt dann den momentanen Zuwachs zu jedem Zeitpunkt, ist also ein Maß für die Neuansteckungen. Der naheliegende Ansatz ist nun zu sagen, dass zu jedem Zeitpunkt die Anzahl der Infizierten, also , proportional zur Anzahl der Begegnungen zwischen Infizierten und Nichtinfizierten ist und damit proportional zur Anzahl der Neuinfektionen, also zu (für Einschränkungen zu dieser Überlegung siehe weiter unten). Dies führt zur Beziehung
mit einem konstanten Proportionalitätsfaktor , der ein Maß für die Ansteckungswahrscheinlichkeit ist und vom Virus, der Saison, vom Abstandsverhalten der Bevölkerung u. Ä. abhängt. Wir haben also eine Beziehung zwischen der gesuchten Funktion und ihrer Ableitung, die in jedem Moment gilt und für die Ausbreitung eines Virus charakteristisch sein sollte. Ein solcher Zusammenhang zwischen einer Funktion und ihrer Ableitung heißt eine gewöhnliche Differentialgleichung. Wenn eine solche Differentialgleichung vorliegt, fragt man sich, welche Funktionen diese Gleichung erfüllen. Dies ist im Allgemeinen schwierig. Im vorliegenden Fall lässt sich direkt durch Ableiten bestätigen, dass die Funktionen
mit Lösungen sind. Der Vorfaktor ist dabei durch
festgelegt, also durch den Wert der Funktion zum Zeitpunkt , und das im Exponenten ist direkt der Proportionalitätsfaktor aus der Differentialgleichung. Wegen
ist der Vorfaktor im Wesentlichen eine Verschiebung im Zeitargument, und kann man durch eine Umskalierung der Zeit zu normieren. Man kann nun sogar zeigen, dass die Exponentialfunktionen die einzigen Funktionen sind, die diese Differentialgleichung erfüllen, siehe Aufgabe 20.37 bzw. Aufgabe 28.5. Dies bedeutet, dass eine Virusausbreitung durch den Faktor und dem Wert an einem einzigen Zeitpunkt eindeutig bestimmt ist. Dies ist ein Spezialfall des Satzes, dass ein Anfangswertproblem eine eindeutige Lösung besitzt, von dem wir verschiedene Varianten kennenlernen werden.
Kommen wir nun zu einigen Einschränkungen der oben formulierten Modellierung. Zunächst ist klar, dass die Exponentialfunktion zu jeder Basis gegen unendlich geht, es aber nur endlich viele Menschen gibt. Also kann irgendwas nicht stimmen. Der Punkt ist, dass in unserer Modellierung die Anzahl der Infizierten zur Anzahl der Begegnungen von Infizierten mit der Gesamtbevölkerung proportional ist, aber nicht mit der Anzahl der Begegnungen mit den Nichtinfizierten. Dieser Unterschied ist zu Beginn der Ausbreitung unerheblich, da zu Beginn die Gesamtbevölkerung nahezu vollständig nicht infiziert ist. Im Verlauf der Epidemie, wenn sich der Durchseuchungsgrad erhöht, wird es zunehmend wahrscheinlicher, dass sich Infizierte und Infizierte begegnen, was zu keiner Neuansteckung führt.
Ferner haben wir ignoriert, dass die Genesenen nicht mehr andere Leute anstecken können. Hier muss man den Unterschied zwischen infiziert und akut infiziert berücksichtigen. Dieser Unterschied ist für den Anfangsverlauf der Ausbreitung ebenfalls unerheblich, spielt aber im späteren Verlauf eine wichtige Rolle. Die Neuansteckung ist also proportional zur Anzahl der akut Infizierten, dies ist die Differenz zwischen der Gesamtinfiziertenzahl und der Gesamtinfiziertenzahl vor einem gewissen Genesungszeitraum (bei Corona ca. Wochen). Dies führt auf die Bedingung
man spricht von einer Differentialgleichung mit Verzögerung, was wir nicht behandeln werden. Für den ersten Zeitraum der Länge nach Ausbruch spielt der Korrekturterm aber keine Rolle.
Schließlich ist der Faktor keine Konstante, sondern wird durch politische Maßnahmen und Verhaltensregeln beeinflusst.
Welche Bewegung vollzieht ein Löwenzahnfallschirmchen? Das Fallschirmchen lässt sich zu jedem Zeitpunkt von dem Wind tragen, der an der Stelle herrscht, wo es sich gerade befindet. Der Wind, seine Stärke und seine Richtung, hängt sowohl von der Zeit als auch vom Ort ab. Das bedeutet, dass hier ein gewisser „Rückkopplungsprozess“ vorliegt: Die bisherige Bewegung (also die Vergangenheit) bestimmt, wo sich das Fallschirmchen befindet und damit auch, welcher Wind auf es einwirkt und damit den weiteren Bewegungsablauf. Solche Bewegungsprozesse werden durch Differentialgleichungen beschrieben.
Differentialgleichungen sind ein fundamentaler Bestandteil der Mathematik und der Naturwissenschaften. Sie drücken eine Beziehung zwischen einer abhängigen Größe (häufig ) und der Änderung dieser Größe () aus. Viele Gesetzmäßigkeiten in der Natur wie Bewegungsprozesse, Ablauf von chemischen Reaktionen, Wachstumsverhalten von Populationen werden durch Differentialgleichungen beschrieben. Hier besprechen wir nur solche Differentialgleichungen, die durch Integration gelöst werden können.
Die Vektorfelder werden im Folgenden nicht immer auf ganz definiert sein, sondern auf einer offenen Menge . Dabei heißt offen, wenn es zu jedem Punkt eine offene Ballumgebung gibt, die ganz in liegt.
Es sei eine offene Teilmenge und es sei
eine Funktion. Dann nennt man
die (gewöhnliche) Differentialgleichung zu (oder zum Vektorfeld oder zum Richtungsfeld ).
Dabei ist erstmal nur ein formaler Ausdruck, dem wir aber sofort eine inhaltliche Interpretation geben. Das soll eine Funktion in einer Variablen repräsentieren und ihre Ableitung. Dies wird präzisiert durch den Begriff der Lösung einer Differentialgleichung.
Es sei eine offene Teilmenge und es sei
eine Funktion. Zur gewöhnlichen Differentialgleichung
heißt eine Funktion
auf einem (mehrpunktigen) Intervall eine Lösung der Differentialgleichung, wenn folgende Eigenschaften erfüllt sind.
- Es ist für alle .
- Die Funktion ist differenzierbar.
- Es ist für alle .
Statt Lösung sagt man auch Lösungsfunktion oder Lösungskurve. Es sei betont, dass anders als bei vielen Gleichungen wie quadratische Gleichungen oder lineare Gleichungssysteme, wo die Lösung eine Zahl oder ein Vektor ist, die Lösungen von Differentialgleichungen Funktionen sind.
Differentialgleichungen beschreiben häufig physikalische Prozesse, insbesondere Bewegungsprozesse. Daran soll auch die Notation erinnern, es steht für die Zeit und für den Ort. Dabei ist hier der Ort eindimensional, d.h. die Bewegung findet nur auf einer Geraden statt. Den Wert sollte man sich als eine zu einem Zeit- und Ortspunkt vorgegebene Richtung auf der Ortsgeraden vorstellen. Eine Lösung ist dann eine Funktion
die differenzierbar ist und deren Ableitung, vorgestellt als Momentangeschwindigkeit, zu jedem Zeitpunkt mit dem durch gegebenen Richtungsvektor übereinstimmt. In Analysis II werden wir auch Bewegungen betrachten, die sich in der Ebene oder im Raum abspielen, und die durch ein entsprechendes Richtungsfeld gesteuert werden.
Die Lösung einer Differentialgleichung ist im Allgemeinen nicht eindeutig, man muss noch Anfangsbedingungen festlegen.
Es sei eine offene Teilmenge und es sei
eine Funktion. Es sei vorgegeben. Dann nennt man
das Anfangswertproblem zur gewöhnlichen Differentialgleichung mit der Anfangsbedingung .
Es sei eine offene Teilmenge und es sei
eine Funktion. Es sei vorgegeben. Dann nennt man eine Funktion
auf einem Intervall eine Lösung des Anfangswertproblems
wenn eine Lösung der Differentialgleichung ist und wenn zusätzlich
gilt.
Es gibt kein allgemeines Verfahren eine Differentialgleichung bzw. ein Anfangswertproblem explizit zu lösen. Die Lösbarkeit hängt wesentlich von der gegebenen Funktion ab.
Das eine Differentialgleichung beschreibende Vektorfeld hängt im Allgemeinen von beiden Variablen und ab. Einfache, aber keineswegs triviale Spezialfälle von Differentialgleichungen liegen vor, wenn das Vektorfeld nur von einer der beiden Variablen abhängt.
- Ortsunabhängige Differentialgleichungen
Eine gewöhnliche Differentialgleichung
heißt ortsunabhängig, wenn die Funktion nicht von abhängt, wenn also mit einer Funktion in der einen Variablen gilt.
Eine ortsunabhängige gewöhnliche Differentialgleichung
zu einer stetigen Funktion ist nichts anderes als das Problem, eine Stammfunktion von zu finden; eine Lösung der Differentialgleichung ist ja genau durch die Bedingung ausgezeichnet, dass ist. Da eine Stammfunktion nur bis auf die Integrationskonstante bestimmt ist, besitzt ein ortsunabhängiges Anfangswertproblem eine eindeutige Lösung.
Wir betrachten das ortsunabhängige Anfangswertproblem
Die Funktion besitzt die Partialbruchzerlegung
daher sind die Stammfunktionen (wir beschränken uns auf ) gleich
Die Anfangsbedingung führt auf
also ist
und die Lösungsfunktion des Anfangswertproblems ist
Wir betrachten das ortsunabhängige Anfangswertproblem
Es ist
sodass eine rationale Funktion in der Exponentialfunktion vorliegt, die wir nach Lemma 27.1 über die Substitution lösen können. Das transformierte Integral ist dabei
Eine Stammfunktion dazu ist
Somit ist
eine Stammfunktion von . Für das Anfangswertproblem setzen wir
an. Dies führt auf
also ist
die Lösung des Anfangswertproblems.
- Zeitunabhängige Differentialgleichungen
Eine gewöhnliche Differentialgleichung
heißt zeitunabhängig, wenn die Funktion nicht von abhängt, wenn also mit einer Funktion in der einen Variablen gilt.
Bei einer zeitunabhängigen Differentialgleichung hängt nur das zugrunde liegende „Vektorfeld“ nicht von der Zeit ab, die Lösungsfunktionen sind hingegen im Allgemeinen zeitabhängig.
Wir betrachten die zeitliche Entwicklung einer Population, die durch folgende Eigenschaften charakterisiert ist.
- Die Individuen der Population leben ewig.
- Alle Individuen beteiligen sich ab ihrer Geburt mit gleichem (durchschnittlichen) Engagement und Erfolg an der Fortpflanzung.
- Zeugung und Geburt finden gleichzeitig statt.
- Der Fortpflanzungserfolg eines Individuums ist unabhängig von der Größe der Gesamtpopulation.
Unter diesen Bedingungen ist die Vermehrung, also der Zuwachs der Population, allein von der momentanen Populationsgröße abhängig und proportional zu dieser. Wenn man die Populationsentwicklung als ansetzt, so erhält man eine gewöhnliche Differentialgleichung
(oder kurz ) mit einer Konstanten . Die Lösungsfunktionen sind
(wobei im Populationsbeispiel ist). Man spricht von exponentiellem Wachstum der Population, und zwar unabhängig davon, ob groß oder klein ist.
Eine Wüste (oder ein Kornblumenfeld) sei kreisrund und breite sich mit der Zeit kontinuierlich aus, indem die Grenze gleichmäßig nach außen geschoben werde, und zwar pro Zeiteinheit um einen gewissen Vortrieb. Die Fläche der Wüste werde durch die Funktion beschrieben. Die Grenze der Wüste hat somit die Länge und diese Länge ist proportional zum Wüstenzuwachs zum Zeitpunkt . Es ergibt sich daher eine Differentialgleichung
mit einer Konstanten . Die Lösungen haben die Form
wie man direkt durch Ableiten bestätigen kann.
- Differentialgleichungen höherer Ordnung
Viele physikalische Bewegungsprozesse sind nicht dadurch determiniert, dass zu jedem Zeit- und Ortspunkt die Bewegungsrichtung (also die gerichtete Geschwindigkeit) vorgegeben wird, sondern dadurch, dass zu jedem Zeit- und Ortspunkt eine Kraft auf ein Teilchen wirkt, die dieses beschleunigt. In diesem Fall kann die Bewegung also nicht durch die erste Ableitung (Geschwindigkeit) modelliert werden, sondern durch die zweite Ableitung (Beschleunigung). Typische Beispiele hierzu sind die durch die Gravitation oder eine Federkraft hervorgerufenen Bewegungen.

Ein Gegenstand der Masse wird im Vakuum aus einer Höhe zum Zeitpunkt losgelassen und fällt unter dem Einfluss der Gravitation zu Boden (freier Fall im Vakuum). Dabei wirkt auf den Körper die Gravitationskraft (die Erdbeschleunigung nehmen wir für diesen Bewegungsvorgang als konstant an), die ihn nach dem Gesetz „Kraft ist Masse mal Beschleunigung“ beschleunigt. Die Beschleunigung ist also konstant und unabhängig von der Masse. Dies bedeutet, dass die Geschwindigkeit des Körpers die Differentialgleichung
erfüllt (die Wahl des Vorzeichens bewirkt, dass der Körper ins Negative fällt). Die durch die Anfangsbedingung (der Gegenstand ruhe zum Zeitpunkt ) festgelegte Lösung für die Geschwindigkeit ist daher
Der zurückgelegte Weg des Körpers ergibt sich wiederum aus der Differentialgleichung
die besagt, dass die Ableitung des Weges nach der Zeit die Momentangeschwindigkeit beschreibt. Die Lösung davon ist
Den Gesamtvorgang kann man durch die Differentialgleichung zweiter Ordnung
ausdrücken.
Ein Gegenstand der Masse wird aus der Höhe losgelassen und fällt unter dem Einfluss der Gravitation zu Boden. Dabei wirkt auf den Körper einerseits die Gravitationskraft (die Erdbeschleunigung nehmen wir für diesen Bewegungsvorgang als konstant an), die ihn beschleunigt, andererseits wird diese Beschleunigung durch den Luftwiderstand verringert. Nach einem physikalischen Gesetz ist die Reibung (bei relativ kleinen Geschwindigkeiten) proportional und entgegengesetzt zur Geschwindigkeit des Körpers. Es sei der Reibungswiderstand, also dieser Proportionalitätsfaktor. Die auf den Körper (nach unten) wirkende Gesamtkraft ist daher
Wegen
gilt daher für diesen Bewegungsvorgang die Differentialgleichung zweiter Ordnung
Wenn wir dies mit der Ableitungsfunktion schreiben, so erhalten wir die Bedingung
die nach Beispiel 29.11 die Lösungen
besitzt. Durch Intergration erhält man für die Differentialgleichung zweiter Ordnung die Lösungsfunktionen
mit beliebigen Konstanten . Siehe auch Aufgabe 29.21.
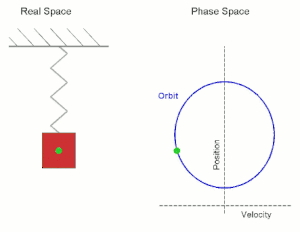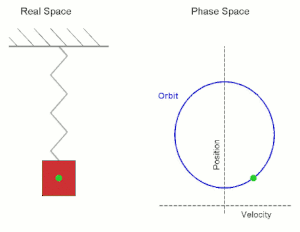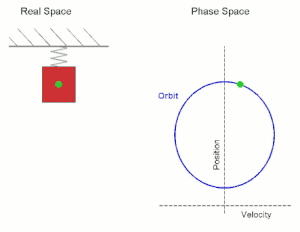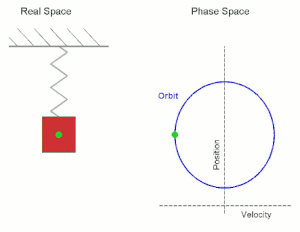
Wir betrachten die Bewegung eines Punktes auf einer Geraden, wobei die auf den Punkt (in Richtung des Nullpunkts) wirkende Kraft (bzw. Beschleunigung) proportional zur Lage des Punktes sein soll. Wenn der Punkt sich in befindet und sich in die positive Richtung bewegt, so wirkt diese Kraft bremsend, wenn er sich in die negative Richtung bewegt, so wirkt die Kraft beschleunigend. Mit der Proportionalitätskonstante gelangt man zur Differentialgleichung (zweiter Ordnung)
die diesen Bewegungsvorgang beschreibt. Als Anfangsbedingung wählen wir und , zum Zeitpunkt soll die Bewegung also durch den Nullpunkt gehen und dort die Geschwindigkeit besitzen. Man kann sofort die Lösung
angeben.
| << | Kurs:Analysis (Osnabrück 2021-2023)/Teil I | >> |
|---|