Kurs:Mathematik (Osnabrück 2009-2011)/Teil III/Vorlesung 76

Das Konzept einer Mannigfaltigkeit

In der zweiten Hälfte dieses Kurses werden wir den Begriff der Mannigfaltigkeit entwickeln. Als Beispiel betrachten wir die Erde (ihre Oberfläche), die in der Wissenschaftsgeschichte lange für eine Scheibe gehalten wurde, und zwar aus gutem Grund. Sie sieht nämlich lokal aus wie eine Ebene. Dies spiegelt sich auch in den Karten wider, die man sich von ihr macht. Eine Karte ist ein ebenes „Blatt“, dessen Punkte in Bijektion zu einem Ausschnitt der Erdoberfläche steht. Insbesondere bei kleinen Ausschnitten halten wir das für unproblematisch, bei Karten aber, die große Ausschnitte oder gar die gesamte Erde wiedergeben sollen, tauchen schnell Fragen auf, was die Karte richtig wiedergibt und was nicht, Fragen nach der Längentreue, Flächentreue, Winkeltreue, Fragen über fehlende Punkte oder mehrfach auftretende Punkte, Fortsetzungsfragen, Krümmungsfragen ...

Beispiel

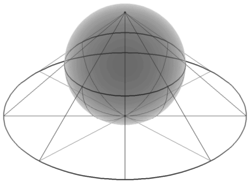
Wir betrachten die Kugeloberfläche

${}K={\left\{(x,y,z)\mid x^{2}+y^{2}+z^{2}=1\right\}}\,$

und nennen den Punkt ${}N=(0,0,1)$ Nordpol und den Punkt ${}S=(0,0,-1)$ Südpol. Ein Punkt ${}P=(x,y,z)\in K$, ${}P\neq N$, definiert zusammen mit dem Nordpol eine eindeutige Gerade im Raum, die durch

$(tx,ty,1+t(z-1))=(0,0,1)+t((x,y,z)-(0,0,1)),\,t\in \mathbb {R} ,$

parametrisiert ist. Der Vektor ${}(x,y,z)-(0,0,1)$, der diese Gerade definiert, ist nicht parallel zur ${}x-y$-Ebene, d.h. dass es genau einen Schnittpunkt dieser Geraden mit dieser Ebene gibt. Dieser ergibt sich zum Parameter

${}t={\frac {1}{1-z}}\,,$

es handelt sich um den Punkt

${\left({\frac {x}{1-z}},{\frac {y}{1-z}},0\right)}.$

Wir fassen diese Konstruktion als eine Abbildung

$\alpha \colon K\setminus \{N\}\longrightarrow \mathbb {R} ^{2},\,(x,y,z)\longmapsto {\left({\frac {x}{1-z}},{\frac {y}{1-z}}\right)}$

auf. Es ist anschaulich klar, dass diese Abbildung eine Bijektion ist, was sich auch einfach über die Formeln nachrechnen lässt. Die Umkehrabbildung ergibt sich, indem man einen Punkt ${}(u,v,0)$ der Ebene mit dem Nordpol verbindet und den Durchstoßungspunkt ${}\neq N$ mit der Kugeloberfläche berechnet. Dies führt zur Bedingung

${}{\begin{aligned}\Vert {(0,0,1)+a((u,v,0)-(0,0,1))}\Vert ^{2}&=\Vert {(au,av,1-a)}\Vert ^{2}\\&=a^{2}u^{2}+a^{2}v^{2}+(1-a)^{2}\\&=1,\end{aligned}}$

was auf

${}a{\left(au^{2}+av^{2}-2+a\right)}=0\,$

führt. Die Lösung ${}a=0$ entspricht dem Nordpol, an der wir nicht interessiert sind, sodass wir auf ${}a={\frac {2}{u^{2}+v^{2}+1}}$ geführt werden, also auf die Abbildung

$\mathbb {R} ^{2}\longrightarrow K\setminus \{N\},\,(u,v)\longmapsto {\left({\frac {2u}{u^{2}+v^{2}+1}},{\frac {2v}{u^{2}+v^{2}+1}},1-{\frac {2}{u^{2}+v^{2}+1}}\right)}.$

Insbesondere ist also die reelle Ebene homöomorph zur in einem Punkt „gelochten“ Kugeloberfläche.

Eine entsprechende Überlegung kann man für ${}K\setminus \{S\}$ anstellen. Dies führt zur Abbildung

$\beta \colon K\setminus \{S\}\longrightarrow \mathbb {R} ^{2},\,(x,y,z)\longmapsto {\left({\frac {x}{z+1}},{\frac {y}{z+1}}\right)}$

mit der Umkehrabbildung

$\mathbb {R} ^{2}\longrightarrow K\setminus \{S\},\,(s,t)\longmapsto {\left({\frac {2s}{s^{2}+t^{2}+1}},{\frac {2t}{s^{2}+t^{2}+1}},-1+{\frac {2}{s^{2}+t^{2}+1}}\right)}.$

Der Südpol entspricht bei der ersten Abbildung dem Mittelpunkt der euklidischen Ebene und der Nordpol entspricht bei der zweiten Abbildung dem Mittelpunkt der euklidischen Ebene. Wir nennen beide Abbildungen bzw. ihre Umkehrabbildungen Karten. Beide Karten decken zusammen die gesamte Kugeloberfläche ab. Da es sich um Homöomorphismen handelt, geben sie die wesentlichen topologischen Eigenschaften der Sphäre richtig wieder. Sie sind beide nicht für die Geographie der Erde gut geeignet, da die Karten die gesamte Ebene benötigen und die Längen sehr stark verzerren.

Beide Karten sind gleich gut. Es ist einfach, Punkte (und allgemeiner andere Figuren) auf der einen Karte in die andere Karte umzurechnen. Man muss dabei allerdings beachten, dass die beiden Pole nur in einer Karte vertreten sind. Die Punkte der Menge ${}K\setminus \{N,S\}$ finden sich auf beiden Karten, und zwar stehen sie durch beide Karten in Bijektion zu der im Mittelpunkt gelochten Ebene ${}\mathbb {R} ^{2}\setminus \{0\}$. Die Übergangsabbildung (oder der Kartenwechsel) wird durch ${}\psi =\beta \circ {\left(\alpha ^{-1}\!\mid _{\mathbb {R} ^{2}\setminus \{0\}}\right)}$ gegeben. Dabei ist

${}{\begin{aligned}\psi (u,v)&=\beta {\left({\frac {2u}{u^{2}+v^{2}+1}},{\frac {2v}{u^{2}+v^{2}+1}},1-{\frac {2}{u^{2}+v^{2}+1}}\right)}\\&={\left({\frac {\frac {2u}{u^{2}+v^{2}+1}}{2-{\frac {2}{u^{2}+v^{2}+1}}}},{\frac {\frac {2v}{u^{2}+v^{2}+1}}{2-{\frac {2}{u^{2}+v^{2}+1}}}}\right)}\\&={\left({\frac {\frac {u}{u^{2}+v^{2}+1}}{\frac {(u^{2}+v^{2}+1)-1}{u^{2}+v^{2}+1}}},{\frac {\frac {v}{u^{2}+v^{2}+1}}{\frac {(u^{2}+v^{2}+1)-1}{u^{2}+v^{2}+1}}}\right)}\\&={\left({\frac {u}{u^{2}+v^{2}}},{\frac {v}{u^{2}+v^{2}}}\right)}.\end{aligned}}$

Diese Übergangsabbildung induziert nicht nur einen Homöomorphismus zwischen ${}\mathbb {R} ^{2}\setminus \{0\}$ mit ${}\mathbb {R} ^{2}\setminus \{0\}$, was unmittelbar daraus folgt, dass die Kartenabbildungen ${}\alpha$ und ${}\beta$ Homöomorphismen sind, sondern sogar einen Diffeomorphismus. Dies ist direkt aus der Funktionsvorschrift ablesbar; es macht aber keinen Sinn zu sagen, dass die Kartenabbildungen Diffeomorphismen sind, da ja die Kugeloberfläche keine offene Teilmenge im ${}\mathbb {R} ^{3}$ ist. Was bisher fehlt ist eine „differenzierbare Struktur“ auf dieser Oberfläche, um von diffeomorph sprechen zu können.

Eine Mannigfaltigkeit ist ein geometrisches Gebilde, das „lokal“ so aussieht wie der euklidische Raum ${}\mathbb {R} ^{n}$. Dabei setzen wir dieses geometrische Gebilde als einen topologischen Raum an, und lokal wird dadurch präzisiert, dass es eine Überdeckung aus offenen Mengen gibt, die homöomorph zu offenen Teilmengen des ${}\mathbb {R} ^{n}$ sind. Obwohl wir im Folgenden mit topologischen Räumen arbeiten sei erwähnt, dass sich der Vorstellungsgehalt des Folgenden nicht verringert, wenn man bei einem topologischen Raum einfach an einen metrischen Raum denkt.

Differenzierbare Mannigfaltigkeiten

Definition

Ein topologischer Hausdorff-Raum ${}M$ heißt eine topologische Mannigfaltigkeit der Dimension ${}n$, wenn es eine offene Überdeckung ${}M=\bigcup _{i\in I}U_{i}$ derart gibt, dass jedes ${}U_{i}$ homöomorph zu einer offenen Teilmenge des ${}\mathbb {R} ^{n}$ ist.

Zu jedem Punkt ${}P\in M$ gibt es also eine offene Umgebung ${}P\in U\subseteq M$, die homöomorph zu einer offenen Teilmenge ${}V\subseteq \mathbb {R} ^{n}$ ist. Sei

$\varphi \colon U\longrightarrow V$

eine Homöomorphie und sei ${}Q=\varphi (P)$. Dann entspricht einer offenen Ballumgebung ${}Q\in U{\left(Q,\epsilon \right)}\subseteq V$ eine offene Umgebung ${}U'=\varphi ^{-1}(U{\left(Q,\epsilon \right)})$ mit ${}P\in U'\subseteq U$, die nach Konstruktion homöomorph zu einem offenen Ball ist. Man kann daher eine topologische Mannigfaltigkeit auch als einen topologischen Hausdorff-Raum charakterisieren, der lokal euklidisch ist.

Definition

Es sei ${}M$ eine topologische Mannigfaltigkeit. Dann nennt man jede Homöomorphie

$\varphi \colon U\longrightarrow V,$

wobei ${}U\subseteq M$ und ${}V\subseteq \mathbb {R} ^{n}$ offen sind, eine (topologische) Karte für ${}M$.

Dabei nennt man die offene Menge ${}U\subseteq M$ manchmal das Kartengebiet und ${}V\subseteq \mathbb {R} ^{n}$ das Kartenbild. Zu einer Karte

$\varphi \colon U\longrightarrow V$

und einer offenen Teilmenge ${}U'\subseteq U$ ist auch die induzierte Abbildung

$\varphi {|}_{U'}\colon U'\longrightarrow \varphi (U')$

wieder eine Karte. Manchmal nennt man auch die Umkehrabbildung eine Karte. Statt Karte spricht man auch von einem lokalen Koordinatensystem. Durch die Karte

${}\varphi \colon U\rightarrow V$ werden ja die Koordinaten auf ${}V\subseteq \mathbb {R} ^{n}$ auf ${}U$ übertragen. Die ${}j$-te Koordinate ${}x_{j}\colon V\rightarrow \mathbb {R}$ induziert die (lokale Koordinaten)-Funktion

$x_{j}\circ \varphi \colon U\longrightarrow \mathbb {R}$

(die oft einfach wieder mit ${}x_{j}$ bezeichnet wird), und ein Punkt ${}Q=(x_{1},\ldots ,x_{n})\in V$ entspricht einem Punkt ${}P=\varphi ^{-1}(Q)$.

Definition

Es sei ${}M$ eine topologische Mannigfaltigkeit, es seien ${}U_{1},U_{2}\subseteq M$ offene Teilmengen und ${}\alpha _{1}\colon U_{1}\rightarrow V_{1}$ und ${}\alpha _{2}\colon U_{2}\rightarrow V_{2}$ seien Karten (mit $V_{1},V_{2}\subseteq \mathbb {R} ^{n}$ offen). Dann heißt die Abbildung

$\alpha _{2}\circ \alpha _{1}^{-1}\colon \alpha _{1}(U_{1}\cap U_{2})\longrightarrow \alpha _{2}(U_{1}\cap U_{2})$

die Übergangsabbildung zu diesen Karten.

Der Durchschnitt ${}U_{1}\cap U_{2}$ ist die offene Teilmenge, auf der beide Karten definiert sind und worauf man die beiden Karten vergleichen kann. Genauer müsste man in der Definition von der Einschränkung von ${}\alpha _{1}^{-1}$ auf die offene Teilmenge ${}\alpha _{1}(U_{1}\cap U_{2})\subseteq V_{1}$ sprechen.

Definition

Es seien ${}n\in \mathbb {N}$ und ${}k\in {\overline {\mathbb {N} }}_{+}$. Ein topologischer Hausdorff-Raum ${}M$ zusammen mit einer offenen Überdeckung ${}M=\bigcup _{i\in I}U_{i}$ und Karten

$\alpha _{i}\colon U_{i}\longrightarrow V_{i}$

mit ${}V_{i}\subseteq \mathbb {R} ^{n}$ offen derart, dass die Übergangsabbildungen

$\alpha _{j}\circ (\alpha _{i})^{-1}\colon V_{i}\cap \alpha _{i}(U_{i}\cap U_{j})\longrightarrow V_{j}\cap \alpha _{j}(U_{i}\cap U_{j})$

${}C^{k}$- Diffeomorphismen für alle ${}i,j\in I$ sind, heißt ${}C^{k}$-Mannigfaltigkeit oder differenzierbare Mannigfaltigkeit (der Dimension ${}n$ vom Differenzierbarkeitsgrad ${}k$). Die Menge der Karten ${}(U_{i},\alpha _{i})$, ${}i\in I$, nennt man auch den ${}C^{k}$-Atlas der Mannigfaltigkeit.

Eine differenzierbare Mannigfaltigkeit ist insbesondere eine topologische Mannigfaltigkeit. Nach unserer Definition ist der Atlas ein integraler Bestandteil des Mannigfaltigkeitsbegriffs. Wichtiger als der Atlas ist aber die durch den Atlas definierte differenzierbare Struktur auf der Mannigfaltigkeit. Dies wird deutlicher, wenn wir den Begriff der differenzierbaren Abbildung zwischen zwei Mannigfaltigkeiten zur Verfügung haben und von diffeomorphen Mannigfaltigkeiten sprechen können.

Definition

Es sei ${}M$ eine differenzierbare Mannigfaltigkeit. Eine offene Teilmenge ${}U\subseteq M$, die mit den eingeschränkten Karten versehen ist, heißt offene Untermannigfaltigkeit.

Beispiel

Jede offene Teilmenge ${}V\subseteq \mathbb {R} ^{n}$ ist eine ${}C^{\infty }$- Mannigfaltigkeit, wenn man die Identität ${}\operatorname {Id} \colon V\rightarrow V$ als Karte nimmt. Die einzige Übergangsabbildung ist dann ebenfalls diese Identität, die ein ${}C^{\infty }$-Diffeomorphismus ist. Dies ist dann eine Mannigfaltigkeit mit einem Atlas, der aus einer einzigen Karte besteht. Man kann aber genauso gut den Atlas nehmen, der aus sämtlichen offenen Teilmengen ${}U\subseteq V$ und den zugehörigen identischen Karten ${}\varphi _{U}$ besteht. Die Übergangsabbildungen sind dann die Identitäten auf ${}U_{1}\cap U_{2}$.

Wir haben schon früher im Kontext des Zwischenwertsatzes von zusammenhängenden metrischen Räumen gesprochen. Die gleiche Definition verwenden wir auch für topologische Räume.

Definition

Ein topologischer Raum ${}X$ heißt zusammenhängend, wenn es in ${}X$ genau zwei Teilmengen gibt (nämlich ${}\emptyset$ und der Gesamtraum $X\neq \emptyset$), die sowohl offen als auch abgeschlossen sind.

Häufig interessiert man sich nur für zusammenhängende Mannigfaltigkeiten, vor allem deshalb, da man im nicht zusammenhängenden Fall die einzelnen „Zusammenhangskomponenten“ getrennt voneinander untersuchen kann. Wir besprechen kurz niedrigdimensionale Mannigfaltigkeiten.

Beispiel

Bei einer nulldimensionalen Mannigfaltigkeit ${}M$ gibt es für jeden Punkt ${}P\in M$ eine offene Umgebung ${}P\in U$, die homöomorph zu einer offenen Menge des ${}\mathbb {R} ^{0}=\{0\}$ ist. D.h. dass die einpunktige Menge ${}\{P\}$ offen sein muss, und daher muss ${}M$ die diskrete Topologie tragen, d.h. jede Teilmenge ist offen. Daher ist die einzige zusammenhängende nulldimensionale Mannigfaltigkeit die einpunktige Menge.

Eine Kreislinie ist eine kompakte eindimensionale Mannigfaltigkeit

Beispiel

An eindimensionalen Mannigfaltigkeiten gibt es zunächst die offenen Teilmengen des ${}\mathbb {R} ^{1}$. Diese sind Vereinigungen von offenen Intervallen, und sie sind genau dann zusammenhängend, wenn sie ein offenes Intervall sind. Jedes offene, beschränkte oder unbeschränkte Intervall ist homöomoph und auch diffeomorph zum offenen Einheitsintervall ${}]0,1[$ und zu den reellen Zahlen ${}\mathbb {R}$ selbst. Die abgschlossenen Intervalle ${}[a,b]$ mit ${}a<b$ sind keine Mannigfaltigkeiten, da es für die Randpunkte (die Intervallgrenzen) keine offene Umgebung gibt, die homöomorph zu einem offenen Intervall ist (sie sind aber sogenannte Mannigfaltigkeiten mit Rand).

Darüber hinaus gibt es noch den Kreis (die Sphäre) ${}S^{1}$ als weitere zusammenhängende eindimensionale Mannigfaltigkeit. Es ist

${}S^{1}={\left\{(x,y)\in \mathbb {R} ^{2}\mid x^{2}+y^{2}=1\right\}}\,.$

Für jeden Punkt ${}P\in S^{1}$ ist ${}S^{1}\setminus \{P\}$ homöomorph zu ${}\mathbb {R}$ (durch stereographische Projektion). Der Kreis ist nicht homöomorph zu ${}\mathbb {R}$, da der Kreis kompakt ist, die reellen Zahlen aber nicht. Neben ${}S^{1}$ und ${}\mathbb {R}$ gibt es keine weiteren eindimensionalen zusammenhängenden Mannigfaltigkeiten mit abzählbarer Basis der Topologie (was hier ohne Beweis erwähnt sei).

Ab der Dimension zwei ist es ohne starke zusätzliche Voraussetzungen nicht möglich, sich eine Übersicht über alle Mannigfaltigkeiten zu verschaffen.

Fußnoten

<< | Kurs:Mathematik (Osnabrück 2009-2011)/Teil III | >> PDF-Version dieser Vorlesung Arbeitsblatt zur Vorlesung (PDF)