Normen, Metriken, Topologie
Audiokommentierte Folien - Wiki2Reveal
[Bearbeiten]Diese Wikiversityseite ist als Foliensatz für Wiki2Reveal mit Audiokommentaren erstellt worden. Diese Präsentation wird in den Kursen:
verwendet (siehe Wiki2Reveal). Ferner gibt es ein Quiz zu dieser Lernressource.
Topologischer Raum
[Bearbeiten]Ein Topologischer Raum ist der grundlegende Gegenstand der Teildisziplin Topologie der Mathematik. Durch die Einführung einer topologischen Struktur auf einer Menge lassen sich
- intuitive Lagebeziehungen wie „Nähe“ und
- „Konvergenz gegen“ aus den reellen Zahlen bzw. aus dem
auf viele und sehr allgemeine Strukturen übertragen (wie z.B. die Topologie von Funktionenräumen).
Definition - Topologie
[Bearbeiten]Eine Topologie ist ein Mengensystem bestehend aus Teilmengen (offene Mengen genannt) einer Grundmenge , für die die folgenden definierenden Eigenschaften erfüllt sind
- (T1)
- (T2) für alle .
- (T3) Für eine beliebige Indexmenge und für alle gilt: .
Eine Menge zusammen mit einer Topologie auf heißt topologischer Raum .
Bemerkung - abgeschlossene Mengen
[Bearbeiten]Mit der Definition aller offenen Mengen in durch die Topologie sind auch alle abgeschlossenen Mengen als Komplement einer offenen Menge definiert.
Definition - offener Kern einer Menge
[Bearbeiten]Sei in in dem topologischen Raum , dann ist der offene Kern als die "größte" in enthaltene offene Menge definiert:
Bemerkung - offener Kern
[Bearbeiten]Da in der Defintion als Vereinigung von offenen Mengen dargestellt ist, ist offen nach Eigenschaft (T3).
Definition - Abschluss einer Menge
[Bearbeiten]Sei in in dem topologischen Raum , dann ist der Abschluss als die "kleinste" abgeschlossene Menge definiert, die enthält:
Bemerkung - Abschluss einer Menge
[Bearbeiten]Da in der Defintion als Schnitt von abgeschlossenen Mengen mit dargestellt ist, ist als Komplement einer beliebigen Vereinigung von offenen Mengen abgeschlossen:
Definition - Rand einer Menge
[Bearbeiten]Sei eine Menge in dem topologischen Raum , dann der Rand einer Menge aus dem Abschluss der Menge ohne den offenen Kern von . Der Rand wird daher wie folgt definiert:
- .
Bemerkung
[Bearbeiten]Die Mengen sind per Definition offen und wechselseitig bilden die beiden Mengen jeweils die Komplemente zu einander. Damit sind diese beiden Mengen zugleich offen und abgeschlossen. Daher haben die beiden Mengen keine Randpunkte.
Definition - Umgebung
[Bearbeiten]Sei und eine Menge in einem topologischen Raum , dann heißt der Umgebung von , wenn eine offene Menge existiert mit:
Die Menge aller Umgebungen von bzgl. der Topologie wird mit bezeichnet. bezeichnet die Menge aller offenen Umgebungen von .
Definition - Umgebungsbasis
[Bearbeiten]Sei und ein Mengensystem in einem topologischen Raum , dann heißt Umgebungsbasis von , wenn gilt:
- (B1)
- (B2) zu jeder Umgebung eine Umgebung mit
Beispiel
[Bearbeiten]Die Menge der offenen -Umgebungen in mit der vom Betrag erzeugten euklidischen Topologie ist eine Umgebungsbasis von .
Bemerkung
[Bearbeiten]Die Begriff der Umgebungsbasis hilft dabei, Konvergenzaussagen nur für die Umgebungsbasis nachzuweisen und damit auch die Aussagen für beliebige Umgebungen ebenfalls zu erhalten. In der Analysis verwendet man -Umgebungen in Definitionen ohne den topologischen Aspekt der Umgebungsbasis explizit zu thematisieren. Man hat die Aussagen streng genommen nicht für beliebige Umgebungen gezeigt hat, sondern nur für die Umgebungsbasis aus den -Umgebungen.
Definition - Basis der Topologie
[Bearbeiten]Sei ein Mengensystem in einem topologischen Raum , dann heißt Basis von , wenn gilt:
- (BT1)
- (BT2) zu jeder offenen Menge gibt es eine offene Menge mit
Beispiel
[Bearbeiten]Die Menge aller offenen Intervalle ist eine Basis der Topologie in dem topologischen mit der vom Betrag erzeugten euklidischen Topologie .
Bemerkung - Merkhilfe
[Bearbeiten]Für die Unterscheidung der Begriffe
- "Umgebungsbasis" und
- "Basis der Topologie"
für einen topologischen Raum kann man folgende Merkhilfe aus der Terminologie ableiten.
Merkhilfe - Umgebungsbasis
[Bearbeiten]Der Begriff "Umgebungsbasis" enthält den Begriff "Umgebung". Damit ist die Umgebungsbasis eine Teilmenge aller Umgebungen von einem Punkt .
Merkhilfe - Basis der Topologie
[Bearbeiten]Der Begriff der "Basis der Topologie" bezieht auf die "Topologie" - also auf das System aller offenen Menge in dem Raum .
Konvergenz in topologischen Räumen
[Bearbeiten]In der Analysis ist die Konvergenz von Folgen eine zentrale Definition, um darauf aufbauende Begriffe wie Stetigkeit, Differenz und Integrale zu definieren. Folgen mit als Indexmenge sind in allgemeinen topologischen Räumen ungeeignet Konvergenz zu definieren, da die Indexmenge bzgl. der Umgebungsbasis nicht mächtig genug ist. Dies ist nur dann möglich, wenn der topologische Raum eine abzählbare Umgebungsbasis besitzt. Daher geht man entweder zu Netzen oder Filtern über
Beispiel: Topologie auf Texten
[Bearbeiten]In der Regel geht man davon aus, dass Topologien auf mathematischen Räumen definiert werden (z.B. Zahlenräume, Funktionenräume, (topologische) Gruppen, Vektorräume, ...). Die Allgemeinheit der Definition macht es aber auch möglich, eine Topologie auf Texten zu definieren. Dieses Beispiel wurde ergänzt, weil rein anschaulich z.B. Texte in der deutschen Sprache
- eine ähnliche Aussage haben können und
- unterschiedliche Wörter verwenden.
Diese Ähnlichkeit der Semantik oder auch Syntax wird als Übung in "Topologie auf Texten" näher untersucht.
Ähnlichkeit von Wörter durch Metrik beschreiben
[Bearbeiten]Stellen Sie von gesprochenen Wörtern die Buchstabenanzahl und die Menge der vorkommenden Buchstaben als Tabelle dar. Wie kann man aus der tabellarische Aufstellung einen Abstand von Wörtern ableiten. machen Sie dazu einen Vorschlag. Welche Eigenschaften hat die von Ihnen vorgeschlagene Abstandsfunktion. Ist es eine Metrik auf dem Raum der Wörter?
Aufgabe - Abstand zwischen Wörtern
[Bearbeiten]- Betrachten Sie die Wörter "Eimer", "Eimr", "Eimerr". Wie können Sie die Unterschiede der Wörter durch eine Metrik ausdrücken
- Phonetische Ähnlichkeit Wörter "Aihmähr" und "Eimer" haben eine phonetische Ähnlichkeit, aber von der Sequenz von Buchstaben unterscheiden sich die Schreibweisen stark. Wie können Sie Ähnlichkeit von gesprochen Wörtern (Spracherkennung) durch eine phonetische Schreibweise notieren und in dieser Notation der Phoneme eine Ähnlichkeit der Wörter ebenfalls ausdrücken.
Klassifikation topologischer Räume
[Bearbeiten]Bedeutung: Notation Topologie
[Bearbeiten]- (T1) leere Menge und die Grundmenge sind offene Mengen
- (T2) für alle : Der Durchschnitt endlich vieler offener Mengen ist eine offene Menge.
- (T3) Die Vereinigung beliebig vieler offener Mengen ist wieder eine offene Menge.
Semantik: Metrik
[Bearbeiten]Eine Metrik ordnet mit zwei Elementen aus einem Grundraum den Abstand zwischen und zu.
Definition: Metrik
[Bearbeiten]Sei eine beliebige Menge. Eine Abbildung heißt Metrik auf , wenn für beliebige Elemente , und von die folgenden Eigenschaften erfüllt sind:
- (M1) Trennung: ,
- (M2) Symmetrie: ,
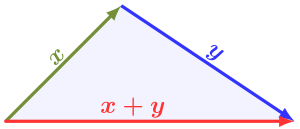
- (M3) Dreiecksungleichung: .
Definition: Metrischer Raum
[Bearbeiten]Sei auf eine Metrik, dann nennt bezeichnet mit eine metrischen Raum.
Aufgabe
[Bearbeiten]Zeigen Sie, dass jeder metrische Raum ein Hausdorff-Raum ist.
Veranschaulichung: Metrik Dreiecksungleichung
[Bearbeiten]Nicht-Negativität
[Bearbeiten]Aus den drei Eigenschaften der Metrik folgt die Nicht-Negativität, d.h. für alle gilt. . Die Nicht-Negativität folgt aus den anderen Eigenschaften mit:
Definition - Halbmetrik
[Bearbeiten]Sei eine beliebige Menge. Eine Abbildung heißt Pseudometrik, Halbmetrik oder Spanne, wenn für beliebige Elemente , und von die folgenden Bedingungen erfüllt sind:
- (HM1) ,
- (HM2) (Symmetrie) und
- (HM3) (Dreiecksungleichung).
Offene Mengen in metrischen Räumen
[Bearbeiten]- In einem metrische Raum definiert man eine Menge als offen (d.h. ), wenn es zu jedem ein gibt, dass die -Kugel ganz in liegt (d.h. )
- Zeigen Sie, dass mit diesem definierten das Paar ein topologischer Raum ist (d.h. (T1), (T2), (T3) erfüllt).
Norm auf Vektorräumen
[Bearbeiten]Eine Norm ist eine Abbildung von einem Vektorraum über dem Körper der reellen oder der komplexen Zahlen in die Menge der nichtnegativen reellen Zahlen . Dabei ordnet die Norm jedem Vektor seine Länge zu.
Definition: Norm
[Bearbeiten]Sei ein -Vektorraum und eine Abbildung Erfüllt die folgenden Eigenschaften N1,N2, N3, so heißt Norm auf .
- (N1) Definitheit: für alle ,
- (N2) absolute Homogenität: für alle und
- (N3) Dreiecksungleichung: für alle .
Definition Halbnorm
[Bearbeiten]Gelten für ein Funktional nur die Bedingungen (N2) und (N3) dann nennt man dieses Funktional Halbnorm.
Bemerkung: N1
[Bearbeiten]Das Eigenschaft (N1) ist eigentlich eine Äquivalenz und es gilt in jedem normierten Raum ( ist der Nullvektor in und ist die Null im Körper , wenn ein -Vektorraum ist).
- (N1)' Definitheit: für alle ,
- Da man für Definitionen ein Minimalitätsprinzip für die definierenden Eigenschaft verwendet, würde man keine stärkere Formulierung (N1)' in der Definition für (N1) verwenden, da die Äquivalenz aus den definierenden Eigenschaften der Norm den Eigenschaften des Vektorraumes bereits für jeden normierten Raum folgen.
Normierter Raum / Metrischer Raum
[Bearbeiten]Ein normierter Raum ist zugleich auch ein metrischer Raum.
- Ein Norm ordnet einem Vektor seine Vektorlänge zu.
- Mit der Norm kann man über eine Metrik definieren, die den Abstand zwischen und angibt.
Aufgabe: Metrik aus gegebener Norm generieren
[Bearbeiten]Sei ein normierter Raum mit der Norm . Zeigen Sie, dass die definierte Abbildung mit die Eigenschaften einer Metrik erfüllt.
Notation: Norm
[Bearbeiten]- In der Eigenschaft (N2) bezeichnet den Betrag des Skalars. ""-Zeichen: Äußere Verknüpfung im Vektorraum bzw. Multiplikation .
- gibt die Länge des Vektors an.
- In (N3) für alle . ""-Zeichen bezeichnet zwei unterschiedliche Verknüpfungen (d.h. Addition in bzw.
Veranschaulichung: Norm Dreiecksungleichung
[Bearbeiten]Def: Konvergenz im normierten Raum
[Bearbeiten]Sei ein normierter Raum und eine Folge in und :
Def: Konvergenz im metrischen Raum
[Bearbeiten]Sei ein metrischer Raum und eine Folge in und :
Def: Cauchy-Folgen in metrischen Räumen
[Bearbeiten]Sei ein metrischer Raum und eine Folge in . heißt Cauchy-Folge in :
Äquivalenz: Normen
[Bearbeiten]Seien zwei Normen und auf dem -Vektorraum gegeben. Die beiden Normen sind äquivalent, wenn gilt:
Zeigen Sie, dass eine Folge genau dann in konvergiert, wenn es auch bzgl. konvergiert.
Äquivalenz von topologieerzeugende Funktionalen
[Bearbeiten]Die Äquivalenz von Normen ist ein Spezialfall von topologieerzeugende Funktionalen, sogenannten Äquivalenz von Gaugefunktionalsystemen.
Betrag in komplexen Zahlen
[Bearbeiten]Sei eine komplexe Zahl mit . Zeigen Sie, dass eine Norm auf dem -Vektorraum ist!
Historische Anmerkung: Norm
[Bearbeiten]Diese axiomatische Definition der Norm wurde von Stefan Banach 1922 in seiner Dissertation aufgestellt. Das heute übliche Normsymbol wurde erstmals von Erhard Schmidt 1908 als Abstand zwischen Vektoren und verwendet.
Aufgaben
[Bearbeiten]In den folgenden Aufgaben geht es darum, definierende Eigenschaften einer Norm, einer Metrik oder allgemein eines topologischen Raumes nachzuweisen.
Aufgabe: Metrische Räume
[Bearbeiten]Zeigen Sie, dass die folgende Abbildung auf mit als Menge der stetigen Abbildungen von dem Intervall nach eine Metrik ist.
- mit
Weisen Sie also die 3 Eigenschaften einer Metrik nach. Berechnen Sie dann den Abstand zwischen den beiden Funktionen und mit und mit !
Optionale Aufgabe: Normierte Räume
[Bearbeiten]Zeigen Sie, dass der metrische Raum mit
nicht vollständig ist. Betrachten Sie dazu z.B. stetige Funktionen, die stückweise aus linearen und konstanten Funktionen definiert sind.
Funktionenfolge definieren
[Bearbeiten]Sei und definieren Sie eine Funktionenfolge mit expliziten Funktionen mit Funktionsterm.
- für alle für alle .
- für alle .
- der Graph von interpoliert die Punkte bzw. und .
Zeigen Sie, dass eine Cauchy-Folge in dem oben definierte Funktionenraum ist und die Folge keinen Grenzwert in besitzt.
Aufgabe: Topologische Räume
[Bearbeiten]Betrachten Sie als Grundmenge des toplogischen Raumes das Intervall und die Mengen , die die Topologie enthalten soll. Erweitern Sie die Erzeugermenge minimal mit weiteren Menge, damit mit zu einem topologischen Raum wird.
- besteht aus 3 offenen Intervallen
- besteht aus 2 offenen Intervallen
- , wobei der Erzeuger der Topologie alle Einpunktmengen aus enthalten soll.
Quiz
[Bearbeiten]Siehe auch
[Bearbeiten]- Topologie auf Texten
- Gaugefunktionale in topologischen Vektorräumen
- Äquivalenz von Gaugefunktionalsystemen
- Netze (Mathematik)
- Hausdorff-Raum
- Grenzen des Folgenbegriffs
- Korrespondenz-Lemma für p-Halbnormen
- Polynomalgebren
- Epidemiologische Distanzen
- Normenäquivalenzsatz
- Topologische Algebra
- COVID-19/Mathematische Modellbildung - für epidemiologische Distanzen im Unterschied zu euklidischen Distanzen in einem Vektorraum.
- Kurs:Topologische Invertierbarkeitskriterien
- Konvexkombination
- Cauchy-Folgen
- Kurs:Maßtheorie auf topologischen Räumen
Seiteninformation
[Bearbeiten]Diese Lernresource wurde als Wiki2Reveal Foliensatz erstellt.
Wiki2Reveal
[Bearbeiten]Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Funktionalanalysis erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.
- Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
- Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Normen,%20Metriken,%20Topologie
- siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.
Nächste Inhalte
[Bearbeiten]- Inhalte der Seite basieren auf:
- Diese Seite ist ein PanDocElectron-SLIDE Dokumententyp
- Quelle: Wikiversity DE https://de.wikiversity.org/wiki/Normen,_Metriken,_Topologie
- siehe Wiki2Reveal zur Funktionsweise von Wiki2Reveal.
- Nächste Inhalte des Kurses sind Netze



































































































































![{\displaystyle V:={\mathcal {C}}([a,b],\mathbb {R} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ba935781730b6339df9ea4dd1ed187114eb53e7)

![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)






![{\displaystyle (V,\|\cdot \|):=({\mathcal {C}}([a,b],\mathbb {R} ),\|\cdot \|)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1a73860715f75422c8146a92683eb76c80d4054)

![{\displaystyle [a,b]:=[-2,+2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9451b3a661d5fa0a3726476839a68180364ca8a2)

![{\displaystyle f_{n}:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f98e29dd6e691983a9a4c597d60cab209d01d80)

![{\displaystyle x\notin \textstyle \left[-{\frac {1}{n}},+{\frac {1}{n}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d5f2e385abb02d554707843af0fbbc17ea43e82)





![{\displaystyle ({\mathcal {C}}([a,b],\mathbb {R} ),\|\cdot \|)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9faf376368b91957acc175265ff59f039cf1bbd0)
![{\displaystyle {\mathcal {C}}([a,b],\mathbb {R} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23f380817b9ebaf6a6afb1036f63f41b10311a9b)
![{\displaystyle X:=[0,3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bab48e5d58680a1efb845490e6191cc395a04e9e)





![{\displaystyle {\mathfrak {E}}_{2}:=[0,3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ce37ca966bc492b97878845bbea7161050903e0)
![{\displaystyle X=[0,3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65c39ff738b885a767f94f479d1390de9cf56079)