Kurs:Mathematik für Anwender (Osnabrück 2011-2012)/Teil I/Vorlesung 2
- Körper
Wir werden nun die Eigenschaften der reellen Zahlen besprechen. Grundlegende Eigenschaften von mathematischen Strukturen werden als Axiome bezeichnet. In der Mathematik werden sämtliche Eigenschaften aus den Axiomen logisch abgeleitet. Die Axiome für die reellen Zahlen gliedern sich in algebraische Axiome, Anordnungsaxiome und das Vollständigkeitsaxiom. Die algebraischen Axiome werden im Begriff des Körpers zusammengefasst. Unter algebraischen Eigenschaften versteht man solche Eigenschaften, die sich auf die Rechenoperationen, also die Addition, die Subtraktion, die Multiplikation und die Division, beziehen. Diese Operationen ordnen zwei Elementen der gegebenen Menge , also beispielsweise zwei reellen Zahlen, ein weiteres Element der Menge zu, es handelt sich also um Verknüpfungen.
Eine Menge heißt ein Körper, wenn es zwei Verknüpfungen (genannt Addition und Multiplikation)
und zwei verschiedene Elemente gibt, die die folgenden Eigenschaften erfüllen.
- Axiome der Addition
- Assoziativgesetz: Für alle gilt: .
- Kommutativgesetz: Für alle gilt .
- ist das neutrale Element der Addition, d.h. für alle ist .
- Existenz des Negativen: Zu jedem gibt es ein Element mit .
- Axiome der Multiplikation
- Assoziativgesetz: Für alle gilt: .
- Kommutativgesetz: Für alle gilt .
- ist das neutrale Element der Multiplikation, d.h. für alle ist .
- Existenz des Inversen: Zu jedem mit gibt es ein Element mit .
- Distributivgesetz: Für alle gilt .
Dass all diese Axiome für die reellen Zahlen (und die rationalen Zahlen) mit den natürlichen Verknüpfungen gelten, ist aus der Schule bekannt.
In einem Körper gilt die Klammerkonvention, dass die Multiplikation stärker bindet als die Addition. Man kann daher statt schreiben. Zur weiteren Notationsvereinfachung wird das Produktzeichen häufig weggelassen. Die besonderen Elemente und in einem Körper werden als Nullelement und als Einselement bezeichnet. Nach der Definition müssen sie verschieden sein.
Die wichtigsten Beispiele für einen Körper sind für uns die rationalen Zahlen, die reellen Zahlen und die komplexen Zahlen, die wir in der nächsten Vorlesung kennenlernen werden.
In einem Körper ist zu einem Element das Element mit eindeutig bestimmt. Bei ist auch das Element mit eindeutig bestimmt.
Es sei vorgegeben und seien und Elemente mit . Dann gilt
Insgesamt ist also . Für den zweiten Teil sei mit vorgegeben. Es seien und Elemente mit . Dann ist
Also ist .
Zu einem Element
nennt man das nach diesem Lemma eindeutig bestimmte Element mit
das Negative von und bezeichnet es mit . Es ist
,
da wegen
das Element gleich dem eindeutig bestimmten Negativen von ist.
Statt schreibt man abkürzend und spricht von der Differenz. Die Differenz ist also keine grundlegende Verknüpfung, sondern wird auf die Addition mit dem Negativen zurückgeführt.
Das zu , , nach diesem Lemma eindeutig bestimmte Element mit nennt man das Inverse von und bezeichnet es mit .
Für , , schreibt man auch abkürzend
Die beiden linken Ausdrücke sind also eine Abkürzung für den rechten Ausdruck.
Zu einem Körperelement und wird als das -fache Produkt von mit sich selbst definiert, und bei wird als interpretiert.
Ein „kurioser“ Körper wird im folgenden Beispiel beschrieben. Dieser Körper mit zwei Elementen ist in der Informatik und der Kodierungstheorie wichtig, wird für uns aber keine große Rolle spielen. Er zeigt, dass es nicht für jeden Körper sinnvoll ist, seine Elemente auf der Zahlengeraden zu verorten.
Wir suchen nach einer Körperstruktur auf der Menge . Wenn das neutrale Element einer Addition und das neutrale Element einer Multiplikation sein soll, so ist dadurch schon alles festgelegt, da sein muss, da ein inverses Element bezüglich der Addition besitzen muss, und da in jedem Körper nach Lemma 2.4 (1) gelten muss. Die Operationstafeln sehen also wie folgt aus.
und
Durch etwas aufwändiges Nachrechnen stellt man fest, dass es sich in der Tat um einen Körper
handelt.
Die folgenden Eigenschaften sind für den Körper der reellen Zahlen vertraut, wir beweisen sie aber allein aus den Axiomen eines Körpers. Sie gelten daher für einen jeden Körper.
Es sei ein Körper und seien Elemente aus . Dann gelten folgende Aussagen.
- (Annullationsregel).
(Vorzeichenregel).
- Aus folgt oder (Nichtnullteilereigenschaft).
- (allgemeines Distributivgesetz).
- Es ist . Durch beidseitiges Abziehen (also Addition mit dem Negativen von ) von ergibt sich die Behauptung.
-
(eindeutig bestimmte) Negative von . Die zweite Gleichheit folgt analog.
- Nach (2) ist und wegen folgt die Behauptung.
- Dies folgt auch aus dem bisher Bewiesenen.
- Nehmen wir an, dass
und
beide von verschieden sind. Dann gibt es dazu inverse Elemente
und
und daher ist
.
Andererseits ist aber nach Voraussetzung
und daher ist nach der Annullationsregel
ergibt.
- Dies folgt aus einer Doppelinduktion, siehe Aufgabe 2.10.
- Anordnungseigenschaften der reellen Zahlen
Bekanntlich kann man die reellen Zahlen mit einer Geraden identifizieren. Auf der Zahlengeraden liegen von zwei Punkten einer weiter rechts als der andere, was bedeutet, dass sein Wert größer ist. Wir besprechen nun diese Anordnungseigenschaften der reellen Zahlen.
Die reellen Zahlen erfüllen die folgenden Anordnungsaxiome.
- Für je zwei reelle Zahlen ist entweder oder oder .
- Aus und folgt (für beliebige ).
- Aus folgt (für beliebige ).
- Aus und folgt (für beliebige ).
- Für jede reelle Zahl gibt es eine natürliche Zahl mit .
Die ersten beiden Eigenschaften drücken aus, dass auf eine totale (oder lineare) Ordnung vorliegt; die in (2) beschriebene Eigenschaft heißt Transitivität. Die fünfte Eigenschaft heißt Archimedes-Axiom.
Statt schreibt man auch . Die Schreibweise bedeutet und . Eine wichtige Beziehung in ist, dass äquivalent[1] zu ist. Diese Äquivalenz ergibt sich durch beidseitiges Addieren von bzw. aus dem dritten Axiom. Eine reelle Zahl nennt man positiv, wenn ist, und negativ, wenn ist. Die ist demnach weder positiv noch negativ, und jedes Element ist entweder positiv oder negativ oder null. Die Elemente mit nennt man dann einfach nichtnegativ und die Elemente mit nichtpositiv. Für die entsprechenden Teilmengen der reellen Zahlen schreibt man
oder Ähnliches.
Für reelle Zahlen gelten die folgenden Eigenschaften.
- Es ist .
- Aus und folgt .
- Aus und folgt .
- Es ist .
- Aus folgt für alle .
- Aus folgt für ganze Zahlen .
- Aus folgt .
- Aus folgt .
Beweis
Das folgende Lemma fasst Folgerungen aus dem Archimedes-Axiom zusammen.
- Zu mit gibt es ein mit .
- Zu gibt es eine natürliche Zahl mit .
- Zu zwei reellen Zahlen
gibt es auch eine rationale Zahl
(mit
,
)
mit
(1). Wir betrachten . Aufgrund des
Archimedes-Axioms
gibt es ein mit
.
Da positiv ist, gilt nach
Lemma 2.6 (2)
auch
.
(2). Es ist eine wohldefinierte, nach
Lemma 2.6 (7)
positive reelle Zahl. Aufgrund des Archimedes-Axioms gibt es eine natürliche Zahl
mit
.
Dies ist nach
Lemma 2.6 (8)
äquivalent zuzusatz2
(3). Wegen ist und daher gibt es nach (2) ein mit . Wegen (1) gibt es auch ein mit . Wegen der Archimedes-Eigenschaft gibt es ein mit . Nach Lemma 2.6 (3) gilt daher . Daher gibt es auch ein derart, dass
ist. Damit ist einerseits und andererseits
wie gewünscht.
Für reelle Zahlen , , nennt man
das abgeschlossene Intervall.
das offene Intervall.
das linksseitig offene Intervall.
das rechtsseitig offene Intervall.
Für das offene Intervall wird häufig auch geschrieben. Die Zahlen und heißen die Grenzen des Intervalls (oder Randpunkte des Intervalls), genauer spricht man von unterer und oberer Grenze. Die Bezeichnung linksseitig und rechtsseitig bei den beiden letzten Intervallen (die man auch als halboffen bezeichnet) rühren von der üblichen Repräsentierung der reellen Zahlen als Zahlengerade her, bei der rechts die positiven Zahlen stehen. Manchmal werden auch Schreibweisen wie verwendet. Dies bedeutet nicht, dass es in ein Element gibt, sondern ist lediglich eine kurze Schreibweise für . Für die reellen Zahlen bilden die ganzzahligen Intervalle , , eine disjunkte Überdeckung. Deshalb ist die folgende Definition sinnvoll.
Die Anordnungseigenschaften erlauben es auch, von wachsenden und fallenden Funktionen zu sprechen.
- Der Betrag
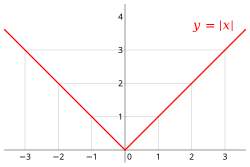
Für eine reelle Zahl ist der Betrag folgendermaßen definiert.
Der Betrag ist also nie negativ und hat nur bei den Wert , sonst ist er immer positiv. Die Gesamtabbildung
nennt man auch Betragsfunktion. Der Funktionsgraph setzt sich aus zwei Halbgeraden zusammen; eine solche Funktion nennt man auch stückweise linear.
erfüllt folgende Eigenschaften (dabei seien beliebige reelle Zahlen).
- Es ist .
- Es ist genau dann, wenn ist.
- Es ist genau dann, wenn oder ist.
- Es ist .
- Es ist .
- Für ist .
- Es ist (Dreiecksungleichung für den Betrag).
- Es ist .
Beweis
- Fußnoten
- ↑ Man sagt, dass zwei Aussagen und zueinander äquivalent sind, wenn die Aussage genau dann wahr ist, wenn die Aussage wahr ist. Dabei sind die beiden Aussagen häufig abhängig von gewissen Variablenbelegungen, und die Äquivalenz bedeutet dann, dass genau dann wahr ist, wenn wahr ist.
| << | Kurs:Mathematik für Anwender (Osnabrück 2011-2012)/Teil I | >> |
|---|
- Äquivalent (MSW)
- Axiom (MSW)
- Klammerkonvention (MSW)
- Nullelement (MSW)
- Einselement (MSW)
- Negative (MSW)
- Differenz (MSW)
- Inverses Element (MSW)
- Annullationsregel (MSW)
- Vorzeichenregel (MSW)
- Nichtnullteilereigenschaft (MSW)
- Allgemeines Distributivgesetz (MSW)
- Totale Ordnung (MSW)
- Archimedes-Axiom (MSW)
- Positiv (MSW)
- Negativ (MSW)
- Nichtnegativ (MSW)
- Nichtpositiv (MSW)
- Grenzen eines Intervalls (MSW)
- Randpunkt (MSW)
- Untere Grenze (MSW)
- Obere Grenze (MSW)
- Halboffen (MSW)
- Überdeckung (MSW)
- Betragsfunktion (MSW)
- Stückweise linear (MSW)
- Dreiecksungleichung für den Betrag (MSW)
- Kurs:Mathematik für Anwender (Osnabrück 2011-2012)/Teil I/Vorlesungen




















































































































































![{\displaystyle {}[a,b]={\left\{x\in \mathbb {R} \mid x\geq a{\text{ und }}x\leq b\right\}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/942a781865320767d856aad71cbf7630b98faea0)
![{\displaystyle {}]a,b[={\left\{x\in \mathbb {R} \mid x>a{\text{ und }}x<b\right\}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6abe1dd0eac46ffe03a32c300251ef6513a77161)
![{\displaystyle {}]a,b]={\left\{x\in \mathbb {R} \mid x>a{\text{ und }}x\leq b\right\}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c0983c9df73dbff86422b5760a99dbdbcdbc4a0)