Kurs:Mathematik für Anwender (Osnabrück 2011-2012)/Teil I/Vorlesung 3

Bernoullische Ungleichung

Die Bernoullische Ungleichung für $n=3$.

Die folgende Aussage heißt Bernoulli-Ungleichung.

Satz

Für jede reelle Zahl ${}x\geq -1$ und eine natürliche Zahl ${}n$

gilt die Abschätzung

${}(1+x)^{n}\geq 1+nx\,.$

Beweis

Wir führen Induktion über ${}n$. Bei ${}n=0$ steht beidseitig ${}1$, sodass die Aussage gilt. Es sei nun die Aussage für ${}n$ bereits bewiesen. Dann ist

${}{\begin{aligned}(1+x)^{n+1}&=(1+x)^{n}(1+x)\\&\geq (1+nx)(1+x)\\&=1+(n+1)x+nx^{2}\\&\geq 1+(n+1)x,\end{aligned}}$

da Quadrate (und positive Vielfache davon) in einem angeordneten Körper nichtnegativ sind.

$\Box$

Die Binomialkoeffizienten

Definition

Zu einer natürlichen Zahl ${}n$ nennt man die Zahl

${}n!:=n(n-1)(n-2)\cdots 3\cdot 2\cdot 1\,$

die Fakultät von ${}n$ (sprich ${}n$ Fakultät).

Man setzt ${}0!=1$.

Definition

Es seien ${}k$ und ${}n$ natürliche Zahlen mit ${}k\leq n$. Dann nennt man

${}{\binom {n}{k}}:={\frac {n!}{k!(n-k)!}}\,$

den Binomialkoeffizienten „${}n$ über ${}k$ “.

Diesen Bruch kann man auch als

${\frac {n(n-1)(n-2)\cdots (n-k+2)(n-k+1)}{k(k-1)(k-2)\cdots 2\cdot 1}}$

schreiben, da die Faktoren aus ${}(n-k)!$ auch in ${}n!$ vorkommen und daher kürzbar sind. In dieser Darstellung stehen im Zähler und im Nenner gleich viele Faktoren. Gelegentlich ist es sinnvoll, auch negative ${}k$ oder ${}k>n$ zuzulassen und in diesen Fällen die Binomialkoeffizienten gleich ${}0$ zu setzen.

Von der Definition her ist es nicht sofort klar, dass es sich bei den Binomialkoeffizienten um natürliche Zahlen handelt. Dies folgt aus der folgenden Beziehung.

Das Dreieck der Binomialkoeffizienten war in Indien und in Persien schon um 1000 bekannt,

in China heißt es Yanghui-Dreieck (nach Yang Hui (um 1238-1298)),

in Europa heißt es das Pascalsche Dreieck (nach Blaise Pascal (1623-1662)).

Lemma

Die Binomialkoeffizienten

erfüllen die rekursive Beziehung

${}{\binom {n+1}{k}}={\binom {n}{k}}+{\binom {n}{k-1}}\,.$

Beweis

Siehe Aufgabe 3.1.

$\Box$

Die folgende Formel bringt die Addition und die Multiplikation miteinander in Beziehung.

Satz

Es seien ${}a,b$ Elemente in einem Körper. Ferner sei ${}n$ eine natürliche Zahl.

Dann gilt

$(a+b)^{n}=\sum _{k=0}^{n}{\binom {n}{k}}a^{k}b^{n-k}.$

Beweis

Wir führen Induktion nach ${}n$. Für ${}n=0$ steht einerseits ${}(a+b)^{0}=1$ und andererseits ${}a^{0}b^{0}=1$. Es sei die Aussage bereits für ${}n$ bewiesen. Dann ist

${}{\begin{aligned}(a+b)^{n+1}&=(a+b)(a+b)^{n}\\&=(a+b){\left(\sum _{k=0}^{n}{\binom {n}{k}}a^{k}b^{n-k}\right)}\\&=a{\left(\sum _{k=0}^{n}{\binom {n}{k}}a^{k}b^{n-k}\right)}+b{\left(\sum _{k=0}^{n}{\binom {n}{k}}a^{k}b^{n-k}\right)}\\&=\sum _{k=0}^{n}{\binom {n}{k}}a^{k+1}b^{n-k}+\sum _{k=0}^{n}{\binom {n}{k}}a^{k}b^{n-k+1}\\&=\sum _{k=1}^{n+1}{\binom {n}{k-1}}a^{k}b^{n-k+1}+\sum _{k=0}^{n+1}{\binom {n}{k}}a^{k}b^{n-k+1}\\&=\sum _{k=1}^{n+1}{\left({\binom {n}{k-1}}+{\binom {n}{k}}\right)}a^{k}b^{n+1-k}+b^{n+1}\\&=\sum _{k=1}^{n+1}{\binom {n+1}{k}}a^{k}b^{n+1-k}+b^{n+1}\\&=\sum _{k=0}^{n+1}{\binom {n+1}{k}}a^{k}b^{n+1-k}.\end{aligned}}$

$\Box$

Bemerkung  

Für den Binomialkoeffizienten

${\binom {n}{k}}$

gibt es eine wichtige inhaltliche Interpretation. Er gibt die Anzahl der ${}k$-elementigen Teilmengen in einer ${}n$-elementigen Menge an. Z.B. gibt es in einer ${}49$-elementigen Menge genau

${}{\binom {49}{6}}={\frac {49\cdot 48\cdot 47\cdot 46\cdot 45\cdot 44}{6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1}}=13983816\,$

${}6$-elementige Teilmengen. Der Kehrwert von dieser Zahl ist die Wahrscheinlichkeit, beim Lotto sechs Richtige zu haben.

Die komplexen Zahlen

Wir führen nun ausgehend von den reellen Zahlen die komplexen Zahlen ein. Zwar haben wir noch nicht alle Eigenschaften der reellen Zahlen kennengelernt, insbesondere haben wir noch nicht die Vollständigkeit diskutiert, die ${}\mathbb {R}$ von ${}\mathbb {Q}$ unterscheidet, doch ist dies für die Konstruktion von ${}{\mathbb {C} }$ unerheblich. Damit haben wir alle für die Anfängervorlesungen relevanten Zahlbereiche zur Verfügung.

Definition

Die Menge ${}\mathbb {R} ^{2}$ mit ${}0:=(0,0)$ und ${}1:=(1,0)$, mit der komponentenweisen Addition und der durch

${}(a,b)\cdot (c,d):=(ac-bd,ad+bc)\,$

definierten Multiplikation nennt man Körper der komplexen Zahlen. Er wird mit

${\mathbb {C} }$

bezeichnet.

Die Addition ist also einfach die vektorielle Addition im ${}\mathbb {R} ^{2}$, während die Multiplikation eine neuartige Verknüpfung ist, die zwar numerisch einfach durchführbar ist, an die man sich aber dennoch gewöhnen muss. Wir werden in Korollar 21.8 (Analysis (Osnabrück 2021-2023)) noch eine geometrische Interpretation für die komplexe Multiplikation kennenlernen.

Lemma

Die komplexen Zahlen

bilden einen Körper.

Beweis

Siehe Aufgabe 3.6.

$\Box$

Wir lösen uns von der Paarschreibweise und schreiben

${}a+b{\mathrm {i} }:=(a,b)\,.$

Insbesondere ist ${}{\mathrm {i} }=(0,1)$, diese Zahl heißt imaginäre Einheit. Diese Zahl hat die wichtige Eigenschaft

${}{\mathrm {i} }^{2}=-1\,.$

Aus dieser Eigenschaft ergeben sich sämtliche algebraischen Eigenschaften der komplexen Zahlen durch die Körpergesetze. So kann man sich auch die obige Multiplikationsregel merken, es ist ja

${}(a+b{\mathrm {i} })(c+d{\mathrm {i} })=ac+ad{\mathrm {i} }+b{\mathrm {i} }c+b{\mathrm {i} }d{\mathrm {i} }=ac+bd{\mathrm {i} }^{2}+(ad+bc){\mathrm {i} }=ac-bd+(ad+bc){\mathrm {i} }\,.$

Wir fassen eine reelle Zahl ${}a$ als die komplexe Zahl ${}a+0{\mathrm {i} }=(a,0)$ auf. In diesem Sinne ist ${}\mathbb {R} \subset {\mathbb {C} }$. Es ist gleichgültig, ob man zwei reelle Zahlen als reelle Zahlen oder als komplexe Zahlen addiert oder multipliziert.

Definition

Zu einer komplexen Zahl

${}z=a+b{\mathrm {i} }\,$

heißt

${}\operatorname {Re} \,{\left(z\right)}=a\,$

der Realteil von ${}z$ und

${}\operatorname {Im} \,{\left(z\right)}=b\,$

heißt der Imaginärteil von ${}z$.

Man sollte sich allerdings die Menge der komplexen Zahlen nicht als etwas vorstellen, was weniger real als andere Zahlensysteme ist. Die Konstruktion der komplexen Zahlen aus den reellen Zahlen ist bei Weitem einfacher als die Konstruktion der reellen Zahlen aus den rationalen Zahlen. Allerdings war es historisch ein langer Prozess, bis die komplexen Zahlen als Zahlen anerkannt wurden; das Irreale daran ist, dass sie einen Körper bilden, der nicht angeordnet werden kann, und dass es sich daher scheinbar um keine Größen handelt, mit denen man sinnvollerweise etwas messen kann.

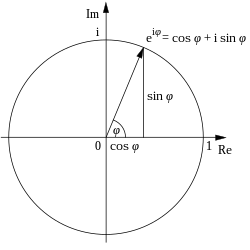
Man kann sich die komplexen Zahlen als die Punkte in einer Ebene vorstellen; für die additive Struktur gilt ja einfach ${}{\mathbb {C} }=\mathbb {R} ^{2}$. In diesem Zusammenhang spricht man von der Gaussschen Zahlenebene. Die horizontale Achse nennt man dann die reelle Achse und die vertikale Achse die imaginäre Achse.

Lemma

Real- und Imaginärteil von komplexen Zahlen erfüllen folgende Eigenschaften (für ${}z$ und ${}w$ aus ${}{\mathbb {C} }$).

1. Es ist ${}z=\operatorname {Re} \,{\left(z\right)}+\operatorname {Im} \,{\left(z\right)}{\mathrm {i} }$.
2. Es ist ${}\operatorname {Re} \,{\left(z+w\right)}=\operatorname {Re} \,{\left(z\right)}+\operatorname {Re} \,{\left(w\right)}$.
3. Es ist ${}\operatorname {Im} \,{\left(z+w\right)}=\operatorname {Im} \,{\left(z\right)}+\operatorname {Im} \,{\left(w\right)}$.
4. Für ${}r\in \mathbb {R}$ ist

   $\operatorname {Re} \,{\left(rz\right)}=r\operatorname {Re} \,{\left(z\right)}{\text{ und }}\operatorname {Im} \,{\left(rz\right)}=r\operatorname {Im} \,{\left(z\right)}.$

5. Es ist ${}z=\operatorname {Re} \,{\left(z\right)}$ genau dann, wenn ${}z\in \mathbb {R}$ ist, und dies ist genau dann der Fall, wenn ${}\operatorname {Im} \,{\left(z\right)}=0$ ist.

Beweis

Siehe Aufgabe 3.7.

$\Box$

Definition

Die Abbildung

${\mathbb {C} }\longrightarrow {\mathbb {C} },\,z=a+b{\mathrm {i} }\longmapsto {\overline {z}}:=a-b{\mathrm {i} },$

heißt komplexe Konjugation.

Zu ${}z$ heißt ${}{\overline {z}}$ die konjugiert-komplexe Zahl von ${}z$. Geometrisch betrachtet ist die komplexe Konjugation zu ${}z\in {\mathbb {C} }$ einfach die Achsenspiegelung an der reellen Achse.

Lemma

Für die komplexe Konjugation gelten die folgenden Rechenregeln (für beliebige ${}z,w\in {\mathbb {C} }$).

1. Es ist ${}{\overline {z+w}}={\overline {z}}+{\overline {w}}$.
2. Es ist ${}{\overline {-z}}=-{\overline {z}}$.
3. Es ist ${}{\overline {z\cdot w}}={\overline {z}}\cdot {\overline {w}}$.
4. Für ${}z\neq 0$ ist ${}{\overline {1/z}}=1/{\overline {z}}$.
5. Es ist ${}{\overline {\overline {z}}}=z$.
6. Es ist ${}{\overline {z}}=z$ genau dann, wenn ${}z\in \mathbb {R}$ ist.

Beweis

Siehe Aufgabe 3.15.

$\Box$

Lemma

Für eine komplexe Zahl ${}z$ gelten die folgenden Beziehungen.

1. Es ist ${}{\overline {z}}=\operatorname {Re} \,{\left(z\right)}-\operatorname {Im} \,{\left(z\right)}{\mathrm {i} }$.
2. Es ist ${}\operatorname {Re} \,{\left(z\right)}={\frac {z+{\overline {z}}}{2}}$.
3. Es ist ${}\operatorname {Im} \,{\left(z\right)}={\frac {z-{\overline {z}}}{2{\mathrm {i} }}}$.

Beweis

Siehe Aufgabe 3.12.

$\Box$

Das Quadrat ${}d^{2}$ einer reellen Zahl ist stets nichtnegativ, und die Summe von zwei nichtnegativen reellen Zahlen ist wieder nichtnegativ. Zu einer nichtnegativen reellen Zahl ${}c$ gibt es eine eindeutige nichtnegative Quadratwurzel ${}{\sqrt {c}}$, siehe Aufgabe 13.5  (das werden wir später beweisen) Daher liefert folgende Definition eine wohldefinierte nichtnegative reelle Zahl.

Definition

Zu einer komplexen Zahl

${}z=a+b{\mathrm {i} }\,$

ist der Betrag durch

${}\vert {z}\vert ={\sqrt {a^{2}+b^{2}}}\,$

definiert.

Der Betrag einer komplexen Zahl ${}z$ ist aufgrund des Satzes des Pythagoras der Abstand von ${}z$ zum Nullpunkt ${}0=(0,0)$. Insgesamt ist der Betrag eine Abbildung

${\mathbb {C} }\longrightarrow \mathbb {R} _{\geq 0},\,z\longmapsto \vert {z}\vert .$

Die Menge aller komplexen Zahlen mit einem bestimmten Betrag bilden einen Kreis mit dem Nullpunkt als Mittelpunkt und mit dem Betrag als Radius. Insbesondere bilden alle komplexen Zahlen mit dem Betrag ${}1$ den komplexen Einheitskreis.

Lemma

Für den Betrag von komplexen Zahlen gelten folgende Eigenschaften.

1. Es ist ${}\vert {z}\vert ={\sqrt {z\ {\overline {z}}}}$.
2. Für reelles ${}z$ stimmen reeller und komplexer Betrag überein.
3. Es ist ${}\vert {z}\vert =0$ genau dann, wenn ${}z=0$ ist.
4. Es ist ${}\vert {z}\vert =\vert {\overline {z}}\vert$.
5. Es ist ${}\vert {zw}\vert =\vert {z}\vert \cdot \vert {w}\vert$.
6. Für ${}z\neq 0$ ist ${}\vert {1/z}\vert =1/\vert {z}\vert$.
7. Es ist ${}\vert {\operatorname {Re} \,{\left(z\right)}}\vert ,\vert {\operatorname {Im} \,{\left(z\right)}}\vert \leq \vert {z}\vert$.
8. Es ist ${}\vert {z+w}\vert \leq \vert {z}\vert +\vert {w}\vert$ (Dreiecksungleichung).

Beweis

Wir zeigen die Dreiecksungleichung, für die anderen Aussagen siehe Aufgabe 3.9. Zunächst gilt nach (7) für jede komplexe Zahl ${}u$ die Abschätzung ${}\operatorname {Re} \,{\left(u\right)}\leq \vert {u}\vert$. Daher ist

${}\operatorname {Re} \,{\left(z{\overline {w}}\right)}\leq \vert {z}\vert \vert {w}\vert \,,$

und somit ist

${}{\begin{aligned}\vert {z+w}\vert ^{2}&=(z+w)({\overline {z}}+{\overline {w}})\\&=z{\overline {z}}+z{\overline {w}}+w{\overline {z}}+w{\overline {w}}\\&=\vert {z}\vert ^{2}+2\operatorname {Re} \,{\left(z{\overline {w}}\right)}+\vert {w}\vert ^{2}\\&\leq \vert {z}\vert ^{2}+2\vert {z}\vert \vert {w}\vert +\vert {w}\vert ^{2}\\&=(\vert {z}\vert +\vert {w}\vert )^{2}.\end{aligned}}$

Durch Wurzelziehen ergibt sich die gewünschte Abschätzung.

$\Box$

Quadratwurzeln von komplexen Zahlen

Die imaginäre Einheit ${}{\mathrm {i} }$ hat die wichtige Eigenschaft ${}{\mathrm {i} }^{2}=-1$. Das Negative von ${}{\mathrm {i} }$ besitzt die gleiche Eigenschaft, nämlich

${}(-{\mathrm {i} })^{2}=(-1)^{2}{\mathrm {i} }^{2}=-1\,.$

Damit gibt es zu jeder negativen reellen Zahl ${}-c$ (mit ${}c$ positiv) in ${}{\mathbb {C} }$ die beiden Quadratwurzeln ${}{\sqrt {c}}{\mathrm {i} }$ und ${}-{\sqrt {c}}{\mathrm {i} }$. Im folgenden Beispiel zeigen wir, dass nicht nur jede reelle Zahl in ${}{\mathbb {C} }$ eine Quadratwurzel besitzt, sondern überhaupt jede komplexe Zahl.

Beispiel

Es sei ${}z=a+b{\mathrm {i} }$ eine komplexe Zahl. Dann hat die komplexe Zahl

${}u={\frac {1}{\sqrt {2}}}{\left(\sigma {\sqrt {\vert {z}\vert +a}}+{\mathrm {i} }{\sqrt {\vert {z}\vert -a}}\right)}\,$

mit dem Vorzeichen

${}\sigma ={\begin{cases}1,{\text{ falls }}b\geq 0\,,\\-1{\text{ falls }}b<0\,,\end{cases}}\,$

die Eigenschaft

${}u^{2}=z\,.$

Insbesondere besitzt also ${}z$ zwei Quadratwurzeln, nämlich ${}u$ und ${}-u$, die bei ${}z=0$ zusammenfallen.

Wir zeigen dies für den Fall

${}b\geq 0\,.$

Dann ist

${}{\begin{aligned}u^{2}&={\left({\frac {1}{\sqrt {2}}}{\left({\sqrt {\vert {z}\vert +a}}+{\mathrm {i} }{\sqrt {\vert {z}\vert -a}}\right)}\right)}^{2}\\&={\frac {1}{2}}{\left(\vert {z}\vert +a-{\left(\vert {z}\vert -a\right)}+2{\mathrm {i} }{\sqrt {{\left(\vert {z}\vert +a\right)}{\left(\vert {z}\vert -a\right)}}}\right)}\\&={\frac {1}{2}}{\left(2a+2{\mathrm {i} }{\sqrt {\vert {z}\vert ^{2}-a^{2}}}\right)}\\&={\frac {1}{2}}{\left(2a+2{\mathrm {i} }{\sqrt {b^{2}}}\right)}\\&={\frac {1}{2}}{\left(2a+2{\mathrm {i} }b\right)}\\&=a+b{\mathrm {i} }.\end{aligned}}$

Daraus ergibt sich, dass innerhalb von ${}{\mathbb {C} }$ jede quadratische Gleichung

${}az^{2}+bz+c=0\,$

mit ${}a,b,c\in {\mathbb {C} },\,a\neq 0$, mindestens eine komplexe Lösung besitzt, siehe Aufgabe 3.16.

Fußnoten

<< | Kurs:Mathematik für Anwender (Osnabrück 2011-2012)/Teil I | >> PDF-Version dieser Vorlesung Arbeitsblatt zur Vorlesung (PDF) (PDF englisch)