Kurs:Topologische Invertierbarkeitskriterien/P-Regularität
Einleitung
[Bearbeiten]Diese Lernresource Wiki2Reveal-Foliensatz zunächst der Zusammenhang zwischen der lokalen Beschränktheit der Topologie und Quasinormen bzw. -Normen hergestellt.
Lokale Beschränktheit der Topologie
[Bearbeiten]Die lokale Beschränktheit der Topologie ist eine topologische Eigenschaft, die über das System der offenen Mengen ausgedrückt wird. Mit offenen Mengen im Kontext der Algebrerweiterungen zu arbeiten ist aber ist aber sehr aufwändig. Daher geht man zu einem topologieerzeugenden Gaugefunktional -Norm bzw. Quasinorm.
Zusammenhang - Lokale Beschränktheit - p-Norm - Quasinorm
[Bearbeiten]Wenn man nachgewiesen hat, dass die lokale Beschränkheit äquivalent zu der -Normierbarkeit der Topologie ist, wird man die -Regularität analog zum Vorgehen bei Banachalgebren bzgl. der Konstruktion der Algebraerweiterungen nach Arens (1958)[1] durchführen können.
Zusammenhang - p-Norm - Quasinorm
[Bearbeiten]Die lokale Beschränkheit ist zudem auch äquivalent zu der Quasinormierbarkeit der Topologie. Damit kann nun auch einen alternativen Beweis für die Algebraerweiterungen mit Quasinorm analog durchführen. Die Quasihalbnormen haben allerdings erst bei der Behandlung der Charakterisierung von PC-regulären Elementen in pseudokonvexen Räumen eine besondere Bedeutung.
Charakterisierung der P-Regularität
[Bearbeiten]Für kommutative lokalbeschränkte Algebren erhält man folgende Charakterisierung:
- permanent singulär (topologischer Nullteiler)
- -regulär es gibt ein mit für alle
Dabei ist eine -Norm bzw. eine Quasinorm.
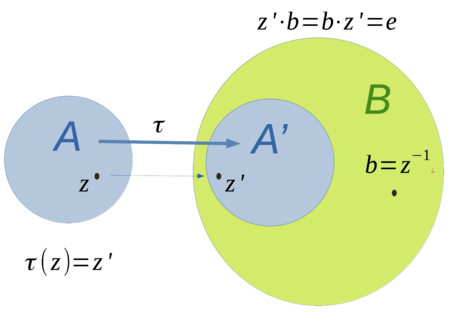
Veranschaulichung - Algebraisomorphismus
[Bearbeiten]P-Regularität über p-Normen bzw. Quasinorm
[Bearbeiten]Mit dieser Äquivalenz von p-Normierbarkeit, lokaler Beschränktheit der Topologie und Quasinormierbeit kann man die Charakterisierung der -Regularität aus Wegen erhalten.
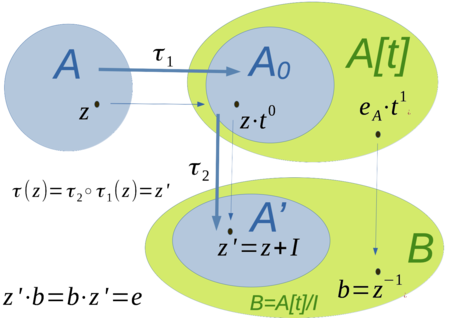
Topologisierung der Polynomalgebra
[Bearbeiten]Ein wesentlicher Schritt für den Beweis des -Regularität auf pseudokonvexen Räumen, bei den die -Halbnormen nicht multiplikativ sind, ist der Zusammenhang zwischen einer -Halbnorm und einer Quasihalbnorm, da dieser Zusammenhang für eine einzelne -Norm und der korrespondierenden Halbnorm gezeigt wird, werden wir hier nicht den Beweis -Regularität für lokal beschränkte bzw. -normierbare Räume direkt führen, sondern den Beweis direkt für korrespondierende Quasinorm führen. Später wird dann das Systems der topologieerzeugenden -Halbnormen durch ein System von Quasihalbnormen ersetzt und für diese System die Algebraerweiterung konstruiert.
Bemerkung: Polynomalgebren
[Bearbeiten]Bei der Konstruktion der Algebraerweiterung, in der ein invertierbar ist, wird in einem ersten Schritt die Algebra der Polynome betrachtet. Die folgende Abbildung zeigt, wie die Algebraerweiterung über die Polynomalgebra konstruiert wird.
Bemerkung: Zusammenhang zwischen p-Norm und Quasinorm
[Bearbeiten]Der Beweis für einen -normierbaren Raum kann analog zur Banachalgebraerweiterungen der -Regularität (nach Arens 1958[1]) geführt werden.
Der Beweis für den Zusammenhang -Norm und einer Quasihalbnorm findet man bei Köthe (1966)[2]
Bemerkung zum Satz über die Quasinormierbarkeit
[Bearbeiten]Ein wesentlicher Teil des Korrespondenzsatzes zwischen p-Normen und Quasinormen nach Köthe[2] ist der Zusammenhang, zwischen eine lokalbeschränkten Topologie auf einem Vektorraum und der Quasinormierbarkeit des Raumes.
Bemerkung zum Satz über die p-Normierbarkeit
[Bearbeiten]Der zweite Teil für den Nachweis des Korrespondenzsatzes zwischen p-Normen und Quasinormen liefert der Zusammenhang, dass jede lokalbeschränkte Topologie auf einem Vektorraum auch durch ein -Norm erzeugt werden kann.
Aufgabe für Studierende
[Bearbeiten]Sei eine topologische Algebra, für die die Topologie durch eine -Norm erzeugt wird.
- (Topologische Nullteiler) Formulieren Sie ein äquivalentes Kriterium für über die -Norm.
- (Homogenität der Norm) Analysieren Sie die Charakterisierung der -Regularität mit bzw. und identifizieren die Stellen, an denen die Homogenität der Norm verwendet die allgemeinere Eigenschaft der -Homogenität ersetzen werden muss?
Definition: Lokalbeschränkt
[Bearbeiten]Sei ein topologischer Vektorraum. Eine Menge heißt beschränkt, falls gilt:
heißt lokalbeschränkt, falls es eine beschränkte Nullumgebung gibt.
Aufgabe für Studierende
[Bearbeiten]Betrachten Sie, den topologische Algebra der stetigen Funktionen mit den Maximumshalbnormen
Mit dem Halbnormensystem ist eine lokalkonvexer Vektorraum.
- Zeigen Sie mit dem Topologisierungslemma, dass eine topologische Algebra mit Multiplikation und für ist.
- Zeigen Sie, dass nicht lokalbeschränkt ist (Beweis durch Widerspruch).
Hinweis zur Aufgabe
[Bearbeiten]- Nehmen Sie an, dass die -Umgebung lokal beschränkt ist. Dabei sei
- Dann verwenden Sie die Funktionenfolge mit folgender Eigenschaft:
Aufgaben - Mengeninklusion
[Bearbeiten]- Zeigen Sie mit den Definitionen von -Umgebung , dass für alle die Teilmengenbeziehung gilt!
- Beschreiben Sie, welche Funktionen in liegen!
Zeichnen der Funktionsgraphen
[Bearbeiten]- Zeichnen Sie die Funktionen und erläutern Sie, dass für alle die Bedingung gilt.
- Ferner gibt es für alle eine Funktion , die nicht in und erläutern Sie, dass für alle die Bedingung gilt und damit die Bedingung .
Satz: Quasinormierbarkeit
[Bearbeiten]Die Topologie eines topologischen Vektorraums kann genau dann durch eine Quasinorm gegeben werden, wenn lokalbeschränkt ist.
Beweis
[Bearbeiten]siehe Satz - Quasinormierbarkeit
Zusammenhang Minkowski-Funktionale und absolut p-konvex Menge
[Bearbeiten]Wenn eine Menge eine absolut p-konvexe Teilmenge eines Vektorraums ist, dann ist das zugehörige Minkowski-Funktional ein -Gaugefunktional mit , das zusätzlich die Dreiecksungleichung für alle erfüllt
Aus diesem Grund wird für die -Regularität wird der Begriff eine absolute -konvexen Mengen als Verallgemeinerung von konvexen Mengen und einer konvexen Mengen benötigt.
Definition: absolut p-konvex
[Bearbeiten]Sei eine Teilmenge eines Vektorraums und , dann heißt absolut -konvex, wenn gilt
Definition: absolut p-konvexe Hülle
[Bearbeiten]Die absolut -konvexe Hülle der Menge (Bezeichnung: ) ist der Schnitt über alle absolut -konvexen Mengen, die enthalten.
Lemma: Darstellung der absolut p-konvexen Hülle
[Bearbeiten]Sei eine Teilmenge eines Vektorraums über dem Kör\-per und , dann läßt sich die absolut -konvexe Hülle von wie folgt schreiben:
Beweisidee
[Bearbeiten]Der vollständige Beweis werden 3 Teilbehauptungen gezeigt, wobei (1) und (2) liefert und (3) die Teilmengenbeziehung .
- (Beweisteil 1) ,
- (Beweisteil 2) ist absolut -konvex und
- (Beweisteil 3) ist in jeder absolut -konvexen Menge enthalten. Für den vollständigen Beweis siehe p-konvexe Hülle.
Satz: p-Normbierbarkeit der Topologie
[Bearbeiten]Ein topologischer Vektorraum ist genau dann -normierbar, wenn dieser eine -konvexe beschränkte Nullumgebung besitzt mit .
Beweis
[Bearbeiten]siehe Satz über die p-Normierbarkeit von topologischen Vektorräume.
Korrespondenzsatz für p-Normen und Quasinormen
[Bearbeiten]Die Topologie eines -normierbaren topologischen Vektorraums kann durch eine Quasinorm erzeugt werden.
Beweis
[Bearbeiten]Jeder -normierbare topologische Vektorraum ist lokal beschränkt und auch jeder Raum ist genau dann quasinormierbar, wenn die Topologie lokal beschränkt. Damit erhält man
- .
Damit sind die drei Begriffe äquivalent für die Eigenschaft der Topologie und man kann für jede -Norm eine korrespondierende Quasinorm finden, die die gleiche Topologie auf erzeugt. .
Zusammenhang von p in der p-Norm und der Stetigkeitskonstante
[Bearbeiten]Umgekehrt soll nun gezeigt werden, dass jeder lokalbeschränkte Raum für ein geeignet gewähltes auch -normierbar ist. Zunächst noch eine Definition die im Zusammenhang mit der Stetigkeitskonstanten der Addition einer Quasinorm steht. Der folgende Beweis zeigt, wie man dieses identifiziert (siehe Köthe[2]).
Definition: Konkavitätsmodul
[Bearbeiten]Sei ein lokalbeschränkter topologischer Vektorraum und eine beschränkte Nullumgebung, dann heißt
- Konkavitätsmodul der Nullumgebung und
- Konkavitätsmodul der Topologie .
Satz: Konkavitätsmodul lokalbeschränkter Räume
[Bearbeiten]Ist der Konkavitätsmodul von einem lokalbeschränkten topologischen Vektorraum , so gibt es zu jedem eine topologieerzeugende -Norm auf .
Bemerkung
[Bearbeiten]Der Konkavitätsmodul liefert Informationen darüber, wie man eine Nullumgebung mit "aufgeblasen" muss, damit beliebige Summe von zwei Elementen aus wieder in der "aufgeblasenen" Nullumgebung liegen.
Beweis
[Bearbeiten]siehe Satz zum Konkavitätsmodul in lokalbeschränkten Algebren.
Zusammenfassung Korrespondenzsatz
[Bearbeiten]Ein topologischer Vektorraum ist genau dann quasinormierbar (d.h. es gibt eine Quasinorm, die die Topologie auf erzeugt), wenn -normierbar ist. In den obigen Beweisen wurde allerdings noch nicht berücksichtigt, dass für die -Regularität auch die Multiplikation stetig sein muss. Dieses erfolgt nun.
Stetigkeit der Multiplikation in der Algebra
[Bearbeiten]Allgemein gibt es mit der Stetigkeit der Multiplikation in einer topologischen Algebra auch für jede Nullumgebung und damit auch für die beschränkte Nullumgebung ein Nullumgebung mit .
Lokalbeschränkte Topologie
[Bearbeiten]Da eine Umgebungsbasis der Topologie darstellt, gibt es mit und man erhält:
Anwendung auf Quasinormen 1
[Bearbeiten]Wendet man diese Mengeninklusion auf die Quasinorm als Minkowski-Funktional der lokalbeschränkten kreisförmigen Nullumgebung an, gilt für alle
und man erhält mit
Anwendung auf Quasinormen 2
[Bearbeiten]Die Eigenschaft der Homogenität der Quasinorm liefert dann
Da die obige Ungleichung für alle gilt, erhält man ebenfalls
Stetigkeitskonstante der Multiplikation
[Bearbeiten]Der Faktor ist hier die Stetigkeitskonstante der Multiplikation, die neben der Konstante aus der Negation der Definition eines topologischen Nullteilers ebenfalls für die Topologisierung der Polynomalgebra berücksichtigt werden muss.
Anwendung auf Quasinormen 3
[Bearbeiten]Die Ungleichung wurde für . Falls oder gilt, ist die Ungleichung sogar eine Gleichheit mit
Aufgabe für Studierende
[Bearbeiten]- Zeigen Sie die obigen Ungleichung für die korrespondierende -Norm zur Quasinorm.
- Erläutern Sie, wie Sie mit der -Homogenität beim Nachweis der Ungleichung für umgehen müssen, damit Sie eine ähnliche Ungleichung erhalten.
- Bestimmen Sie für die Stetigkeitskonstante der Multiplikation mit:
Siehe auch
[Bearbeiten]- Algebraerweiterung
- Konstruktion des Algebraisomorphismus
- Lemma - Subadditivität p-Konvexität
- Normen, Metriken, Topologie
- Minkowski-Funktional
- Konvexkombination
- B-Regularität
- P-Regularität über p-Normen
- P-Regularität über Quasinormen
- MLC-Regularität
- MPC-Regularität
- LC-Regularität
- PC-Regularität
- Topologisierungslemma für Algebren
- Topologische Nullteiler
- Satz zur Quasinormierbarkeit
- Satz zur p-Normierbarkeit
- Satz - Konkavitätsmodul
Quellennachweis
[Bearbeiten]- ↑ a b Arens R., Inverse producing extensions of normed algebras, Trans. Amer. Math. Soc. 88, (1958), S. 536-548
- ↑ a b c Gottfried Köthe (1966) Topologische lineare Räume, 15.10, S.162-166.
Seiteninformation
[Bearbeiten]Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.
Wiki2Reveal
[Bearbeiten]Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Topologische Invertierbarkeitskriterien' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.
- Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
- Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Topologische%20Invertierbarkeitskriterien/P-Regularit%C3%A4t
- siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.













![{\displaystyle A[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13daf73f25e64310e7e5d67c5aa8dd4f97cb884f)











![{\displaystyle \|\cdot \|_{n}:=\displaystyle \max _{x\in [-n,n]}|f(x)|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b150bdc500a9ba51cffedff9df6d0181f13c7b8)




































![{\textstyle p\in (0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d5759f236d7ea252b2d4724167f38f65c88f4bb)































