Kurs:Mathematik (Osnabrück 2009-2011)/Teil I/Vorlesung 5
Für zwei natürliche Zahlen gilt genau dann, wenn man mit einem schreiben kann (siehe Aufgabe 4.12). In diesem Fall ist das aufgrund der Abziehregel eindeutig bestimmt und heißt die Differenz von und , geschrieben . Bei gibt es innerhalb von keine Lösung für die Gleichung . Innerhalb der ganzen Zahlen gibt es die negative Lösung .
- Die ganzen Zahlen
Wir wollen die ganzen Zahlen ausgehend von den natürlichen Zahlen konstruieren. Für viele Konstruktionen in der Mathematik ist der Begriff der Äquivalenzrelation entscheidend. Die Strategie ist dabei, zuerst eine „ziemlich große“ Menge zu konstruieren, die alle Elemente der beabsichtigten Menge (in aller Regel mehrfach) „repräsentiert“, und dann Elemente zu „identifizieren“, damit jedes Zielobjekt einen eindeutigen Repräsentanten bekommt.
Es seien und zwei Mengen, auf denen jeweils eine Verknüpfung festgelegt ist. Dann heißt die auf der Produktmenge
(oder komponentenweise Verknüpfung).
Dies ist ein einfacher Begriff, beispielsweise wird auf dem die Vektorraumaddition komponentenweise erklärt. Eigenschaften der Einzelverknüpfungen übertragen sich direkt auf die Produktverknüpfung. Wenn beispielsweise beide Verknüpfungen assoziativ sind, so gilt das auch für die Produktverknüpfung. Wir verwenden den Begriff in der folgenden Konstruktion.
Es sei die Menge der natürlichen Zahlen und die Produktmenge mit der komponentenweisen Addition.[1] Wir erklären auf eine Relation durch[2]
Dies ist bei genau dann der Fall, wenn es ein (nämlich ) mit
gibt. D.h. die beiden Paare unterscheiden sich um ein Diagonalelement, also um ein Paar, wo beide Komponenten übereinstimmen. Diese Relation ist eine Äquivalenzrelation auf , siehe Aufgabe 5.1. Wenn man als ein quadratisches Gitter anordnet (das ist ein „diskretes Koordinatensystem“), so sind die Äquivalenzklassen durch die Punkte auf einer zur Diagonalen parallelen „diskreten Geraden“ gegeben. Die Punkte mit sind äquivalent zu , sie haben also einen Repräsentanten, bei dem die zweite Komponente ist. Die Punkte mit sind äquivalent zu , sie haben also einen Repräsentanten, bei dem die erste Komponente ist. Die Punkte sind zu äquivalent. Den Repräsentanten einer Äquivalenzklasse, bei dem mindestens eine Komponente ist, nennen wir den Standardvertreter dieser Äquivalenzklasse. Die Standardvertreter sind die diskreten Punkte des begrenzenden Viertelkreuzes; zu einem Punkt ergibt sich der Standardvertreter, wenn man parallel zur Diagonalen in Richtung der Halbachsen wandert, bis man auf einer der Halbachsen landet. Zwei Punkte sind genau dann äquivalent, wenn sie den gleichen Standardvertreter besitzen.
Wir bezeichnen nun die Quotientenmenge, also die Menge der Äquivalenzklassen unter dieser Äquivalenzrelation, als Menge der ganzen Zahlen und bezeichnen sie mit . Jede ganze Zahl hat dann genau einen Standardvertreter der Form mit , der Form oder der Form mit . Eine natürliche Zahl fassen wir von nun an als die ganze Zahl auf.
Wir wollen nun zwei ganze Zahlen, also zwei solche Äquivalenzklassen und miteinander „addieren“, also eine Verknüpfung auf einführen. Der naheliegende Ansatz ist, diese Verknüpfung mittels der komponentenweisen Addition als
zu definieren. Hier tritt das Problem der Wohldefiniertheit auf, denn die Verknüpfung wird erklärt unter Bezug auf Repräsentanten, und es ist nicht von vornherein klar, dass unterschiedliche Repräsentanten zum gleichen Ergebnis führen. Wenn also und sind, so muss man überprüfen, dass
und damit ist. Dies ist der Fall, siehe Aufgabe 5.2. Man kann weiterhin zeigen, dass die so definierte Verknüpfung auf assoziativ und kommutativ ist, dass das neutrale Element der Verknüpfung ist und dass es zu jedem Element ein inverses Element gibt, nämlich .
Wir definieren nun eine Multiplikation auf durch
Dies ist wieder wohldefiniert und man kann zeigen, dass die Multiplikation assoziativ und kommutativ ist mit als neutralem Element und dass das Distributivgesetz gilt.
Um die Eigenschaften der Verknüpfungen, die wir auf den ganzen Zahlen haben, prägnant beschreiben zu können, dient der Begriff des kommutativen Ringes.
Ein kommutativer Ring ist eine Menge mit zwei Verknüpfungen und (genannt Addition und Multiplikation) und mit zwei ausgezeichneten Elementen und derart, dass folgende Bedingungen erfüllt sind:
- ist eine kommutative Gruppe.
- Die Multiplikation ist eine assoziative und kommutative Verknüpfung und ist das neutrale Element der Multiplikation.
- Es gilt das Distributivgesetz, also
Von nun an stellen wir uns als eine beidseitige diskrete Zahlengerade vor.
- Körper
Wir werden von nun an den axiomatischen Aufbau der reellen Zahlen besprechen. Diese Axiome gliedern sich in algebraische Axiome, Anordnungsaxiome und das Vollständigkeitsaxiom. Die algebraischen Axiome werden im Begriff des Körpers zusammengefasst. Ein Körper ist ein kommutativer Ring mit , bei dem zusätzlich jedes Element ein Inverses bzgl. der Multiplikation bestizt. In der folgenden Definition werden alle Eigenschaften eines Körpers aufgeführt.
Eine Menge heißt ein Körper, wenn es zwei Verknüpfungen (genannt Addition und Multiplikation)
und zwei verschiedene Elemente gibt, die die folgenden Eigenschaften erfüllen.
- Axiome der Addition
- Assoziativgesetz: Für alle gilt: .
- Kommutativgesetz: Für alle gilt .
- ist das neutrale Element der Addition, d.h. für alle ist .
- Existenz des Negativen: Zu jedem gibt es ein Element mit .
- Axiome der Multiplikation
- Assoziativgesetz: Für alle gilt: .
- Kommutativgesetz: Für alle gilt .
- ist das neutrale Element der Multiplikation, d.h. für alle ist .
- Existenz des Inversen: Zu jedem mit gibt es ein Element mit .
- Distributivgesetz: Für alle gilt .
In einem Körper gilt die Klammerkonvention, dass die Multiplikation stärker bindet als die Addition. Man kann daher statt schreiben. Zur weiteren Notationsvereinfachung wird das Produktzeichen häufig weggelassen. Die besonderen Elemente und in einem Körper werden als Nullelement und als Einselement bezeichnet. Nach der Definition müssen sie verschieden sein.
Die wichtigsten Beispiele für einen Körper sind für uns die rationalen Zahlen und die reellen Zahlen.
Die additiven Körperaxiome kann man so lesen, dass die Menge zusammen mit dem ausgezeichneten Element und der Addition als Verknüpfung eine Gruppe bildet, die zusätzlich kommutativ ist. Ebenso bildet die Menge (also ganz ohne die ) mit dem neutralen Element (das wegen der expliziten Voraussetzung der Körperaxiome von verschieden ist und daher zu gehört) und der Multiplikation eine (ebenfalls kommutative) Gruppe. Wenn ein Körper vorliegt, so hat man also zugleich zwei Gruppen vorliegen, es ist aber falsch zu sagen, dass auf zweifache Weise eine Gruppe ist, da einerseits mit der Addition und andererseits (und eben nicht ) eine Gruppe mit der Multiplikation bildet.
In einem Körper ist zu einem Element das Element mit eindeutig bestimmt. Bei ist auch das Element mit eindeutig bestimmt.
Beweis
Zu einem Element nennt man das nach diesem Lemma eindeutig bestimmte Element mit das Negative von und bezeichnet es mit . Statt schreibt man abkürzend und spricht von der Differenz. Die Differenz ist also keine grundlegende Verknüpfung, sondern wird auf die Addition mit Negativen zurückgeführt.
Das zu , , nach diesem Lemma eindeutig bestimmte Element mit nennt man das Inverse von und bezeichnet es mit .
Für , , schreibt man auch abkürzend
In jedem Körper findet man die natürlichen Zahlen und auch die ganzen Zahlen wieder, und zwar wird die natürliche Zahl als die -fache Summe von mit sich selbst in interpretiert. Entsprechend wird die negative Zahl als die -fache Summe von interpretiert, siehe die Aufgaben. Zu einem Körperelement und wird als das -fache Produkt von mit sich selbst definiert, und bei wird als interpretiert.
Wir wollen ausgehend von der Menge der ganzen Zahlen , die einen kommutativen Ring bildet, die Menge der rationalen Zahlen konstruieren. Wir gehen dabei wieder ähnlich wie bei der Konstruktion der ganzen Zahlen aus den natürlichen Zahlen vor, indem wir auf einer „zu großen“ Menge eine Äquivalenzrelation einführen, sodass die Quotientenmenge ein Modell für die rationalen Zahlen sind.
Wir starten mit der Produktmenge
Zur Orientierung sei schon jetzt gesagt, dass das Paar später den Bruch repräsentieren soll.[3] Auf wollen wir eine Äquivalenzrelation definieren, wobei zwei Paare als äquivalent gelten sollen, wenn sie „den gleichen Bruch“ repräsentieren (den es noch nicht gibt). Wir definieren
Diese Relation wird also unter Bezug auf die Gleichheit in erklärt. Es handelt sich dabei um eine Äquivalenzrelation, wie man direkt nachrechnen kann, siehe Aufgabe 5.6. Die Quotientenmenge unter dieser Äquivalenzrelation nennen wir . Für die Elemente in schreiben wir vorläufig noch .
Es ist hilfreich, sich diese Situation zu veranschaulichen, indem man die diskrete obere Halbebene[4]
betrachtet. Ein Paar ist dann ein Gitterpunkt, wobei wir uns die ganzen Zahlen als die Punkte(wo also die zweite Komponente konstant ist.) bezeichnen wir mit . Ein jeder Punkt definiert eine eindeutige Gerade, die durch diesen Punkt und durch den Nullpunkt verläuft. In dieser geometrischen Interpretation sind zwei Punkte und genau dann äquivalent, wenn sie die gleiche Gerade definieren, und dies ist genau dann der Fall, wenn ihre „Steigungen“ übereinstimmen. Zwei Punkte liegen ja auf der gleichen Geraden genau dann, wenn sie, wenn man durch Streckung ihre zweite Koordinate zur Übereinstimmung bringt, dann auch die erste Koordinate übereinstimmt. Wenn man den ersten Punkt mit streckt (multipliziert) und den zweiten Punkt mit , so erhält man die beiden Punkte und , und die Gleichheit vorne war die Definition für die Relation.
Auch die Identifizierungsabbildung zu dieser Äquivalenzrelation kann man sich gut vorstellen. Der Schnittpunkt der durch einen Punkt definierten Geraden mit der Zahlengeraden ist ein Punkt, der dem Bruch entspricht.
Wir wollen nun auf eine Addition und eine Multiplikation definieren. Wir setzen[5]
Man muss jetzt zeigen, dass diese Verknüpfungen wohldefiniert sind, also unabhängig von der Wahl des Repräsentanten, siehe Aufgabe 5.14. Sodann kann man mit einigem Aufwand nachweisen, dass mit diesen Verknüpfungen und mit den ausgezeichneten Elementen
einen Körper bilden, siehe Aufgabe 5.15. Das Negative eines Elementes ist und das Inverse eines von null verschiedenen Elementes ist (bzw. , falls negativ ist).
Aufgrund von dieser Konstruktion können wir uns die rationalen Zahlen als Punkte auf einer Zahlengeraden vorstellen (in der Konstruktion die Geraden mit .)
Wir suchen nach einer Körperstruktur auf der Menge . Wenn das neutrale Element einer Addition und das neutrale Element einer Multiplikation sein soll, so ist dadurch schon alles festgelegt, da sein muss, da ein inverses Element bezüglich der Addition besitzen muss, und da in jedem Körper nach Lemma 5.9 (1) gelten muss. Die Operationstafeln sehen also wie folgt aus.
und
Durch etwas aufwändiges Nachrechnen stellt man fest, dass es sich in der Tat um einen Körper
handelt.
Es sei ein Körper und seien Elemente aus . Dann gelten folgende Aussagen.
- (Annullationsregel).
(Vorzeichenregel).
- Aus folgt oder (Nichtnullteilereigenschaft).
- (allgemeines Distributivgesetz).
- Es ist . Durch beidseitiges Abziehen (also Addition mit dem Negativen von ) von ergibt sich die Behauptung.
-
(eindeutig bestimmte) Negative von . Die zweite Gleichheit folgt analog.
- Nach (2) ist und wegen folgt die Behauptung.
- Dies folgt auch aus dem bisher Bewiesenen.
- Nehmen wir an, dass
und
beide von verschieden sind. Dann gibt es dazu inverse Elemente
und
und daher ist
.
Andererseits ist aber nach Voraussetzung
und daher ist nach der Annullationsregel
ergibt.
- Dies folgt aus einer Doppelinduktion, siehe Aufgabe 5.17.
- Die Binomialkoeffizienten
Es seien und natürliche Zahlen mit . Dann nennt man
den Binomialkoeffizienten „ über “.
Diesen Bruch kann man auch als
schreiben, da die Faktoren aus auch in vorkommen und daher kürzbar sind. In dieser Darstellung stehen im Zähler und im Nenner gleich viele Faktoren. Gelegentlich ist es sinnvoll, auch negative oder zuzulassen und in diesen Fällen die Binomialkoeffizienten gleich zu setzen.
Von der Definition her ist es nicht sofort klar, dass es sich bei den Binomialkoeffizienten um natürliche Zahlen handelt. Dies folgt aus der folgenden Beziehung.


Die folgende Formel bringt die Addition und die Multiplikation miteinander in Beziehung.
Wir führen Induktion nach . Für steht einerseits und andererseits . Es sei die Aussage bereits für bewiesen. Dann ist
- Fußnoten
| << | Kurs:Mathematik (Osnabrück 2009-2011)/Teil I | >> |
|---|
- ↑ Passende Interpretationen für die Paare in diesem Kontext sind beispielsweise: Das Paar repräsentiert das Ergebnis eines Fußballspieles, wobei die Toranzahl der Heimmannschaft und die Toranzahl der Gastmannschaft repräsentiert, oder: Das Paar repräsentiert das Alter eines menschlichen Paares, wobei für das Alter der Frau und für das Alter des Mannes steht. Der Übergang zu den Äquivalenzklassen bedeutet dann, sich nur noch für die Tordifferenz bzw. den Altersunterschied zu interessieren, nicht mehr für das genaue Ergebnis bzw. das Alter der einzelnen Personen. Man kann auch das Paar als eine Schrittfolge aus Schritten nach rechts und Schritten nach links ansehen.
- ↑ Das Paar wird später die Differenz repräsentieren.
- ↑ Man kann sich vorstellen, dass in die erste Zahl eine Anzahl an Kuchen und die zweite Zahl eine Anzahl von Personen bedeutet.
- ↑ Man könnte auch nehmen.
- ↑ Die Definition der Addition kann man als Addition der Steigung sehen.
- Differenz (MSW)
- Standardvertreter (MSW)
- Menge der ganzen Zahlen (MSW)
- Wohldefiniertheit (MSW)
- Addition (MSW)
- Multiplikation (MSW)
- Distributivgesetz (MSW)
- Klammerkonvention (MSW)
- Nullelement (MSW)
- Einselement (MSW)
- Negative (MSW)
- Inverses Element (MSW)
- Rationale Zahlen (MSW)
- Annullationsregel (MSW)
- Vorzeichenregel (MSW)
- Nichtnullteilereigenschaft (MSW)
- Allgemeines Distributivgesetz (MSW)
- Dreieck der Binomialkoeffizienten (MSW)
- Yanghui-Dreieck (MSW)
- Pascalsches Dreieck (MSW)
- Kurs:Mathematik (Osnabrück 2009-2011)/Teil I/Vorlesungen


















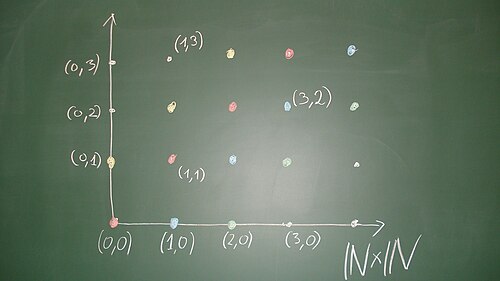






















![{\displaystyle {}[(a,b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad856e5411d0b9ea10ddb04a48932aef19892e7a)
![{\displaystyle {}[(c,d)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b865712c6f9654641f6315839d7fb250d5ed6fa1)

![{\displaystyle {}[(a,b)]\oplus [(c,d)]:=[(a+c,b+d)]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a778629177dd8a896f6ce8cb000f41b321dc395)



![{\displaystyle {}[(a+c,b+d)]=[(a'+c',b'+d')]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b9bc368eabf53b7c89081c97a70ea09b665f4fb)
![{\displaystyle {}[(0,0)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/475a6889495e16a90a7bddd389ad803ee5e078f9)
![{\displaystyle {}[(b,a)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7257885d4524a38fea17a5ad720d33f256cdeaf8)
![{\displaystyle {}[(a,b)]\cdot [(c,d)]:=[(ac+bd,ad+bc)]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e886953fa3c1d350ffa773ec3c5eee3948d2a80c)
![{\displaystyle {}1=[(1,0)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7def7a0131953ef73e591cb841fb440c9b19b53b)




































































![{\displaystyle [(a,b)]+[(c,d)]:=[(ad+bc,bd)]{\text{ und }}[(a,b)]\cdot [(c,d)]=[(ac,bd)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/befa9c93d1b9f9610cc74339da1f55dbb1211643)
![{\displaystyle 0:=[(0,1)]{\text{ und }}1:=[(1,1)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/462ddbe230fcd71a9407c7cd6a1b6ef6713facbf)
![{\displaystyle {}[(-a,b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb5fc95544e383aaaa75c29f2bd3e4cc96b40ae6)
![{\displaystyle {}[(-b,-a)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84b29d3ae234a512f754d83e1f162e573ceacc47)












































