Kurs:Mathematik (Osnabrück 2009-2011)/Teil I/Vorlesung 6

Angeordnete Körper

Definition

Ein Körper ${}K$ heißt angeordnet, wenn es eine totale Ordnung ${}\geq$ auf ${}K$ gibt, die die beiden Eigenschaften

1. Aus ${}a\geq b$ folgt ${}a+c\geq b+c$ (für beliebige ${}a,b,c\in K$),
2. Aus ${}a\geq 0$ und ${}b\geq 0$ folgt ${}ab\geq 0$ (für beliebige ${}a,b\in K$),

erfüllt.

Statt ${}a\geq b$ schreibt man auch ${}b\leq a$. Die Schreibweise ${}a>b$ bedeutet ${}a\geq b$ und ${}a\neq b$. Eine wichtige Beziehung in einem angeordneten Körper ist, dass ${}a\geq b$ äquivalent zu ${}a-b\geq 0$ ist. Diese Äquivalenz ergibt sich durch beidseitiges Addieren von ${}-b$ bzw. ${}b$ aus dem ersten Axiom. In einem angeordneten Körper nennt man ein Element ${}a\in K$ positiv, wenn ${}a>0$ ist, und negativ, wenn ${}a<0$ ist. Die ${}0$ ist demnach weder positiv noch negativ, und jedes Element ist entweder positiv oder negativ oder null. Die Elemente ${}a$ mit ${}a\geq 0$ nennt man dann einfach nichtnegativ und die Elemente ${}a$ mit ${}a\leq 0$ nichtpositiv. Für die entsprechenden Mengen schreibt man

$K_{+},\,K_{-},\,K_{\geq 0}=K_{+}^{0},\,K_{\leq 0}=K_{-}^{0}$

oder Ähnliches. Die wichtigsten Beispiele für angeordnete Körper sind der Körper der rationalen Zahlen ${}\mathbb {Q}$ und der Körper der reellen Zahlen ${}\mathbb {R}$.

Lemma

In einem angeordneten Körper gelten die folgenden Eigenschaften.

1. ${}1>0$,
2. Aus ${}a\geq b$ und ${}c\geq 0$ folgt ${}ac\geq bc$,
3. Aus ${}a\geq b$ und ${}c\leq 0$ folgt ${}ac\leq bc$.

Beweis

Siehe Aufgabe 6.2.

$\Box$

Definition

Es sei ${}K$ ein angeordneter Körper. Zu ${}a,b\in K$, ${}a\leq b$, nennt man

• ${}[a,b]={\left\{x\in K\mid a\leq x{\text{ und }}x\leq b\right\}}$

das abgeschlossene Intervall.

• ${}]a,b[={\left\{x\in K\mid a<x{\text{ und }}x<b\right\}}$

das offene Intervall.

• ${}]a,b]={\left\{x\in K\mid a<x{\text{ und }}x\leq b\right\}}$

das linksseitig offene Intervall.

• ${}[a,b[={\left\{x\in K\mid a\leq x{\text{ und }}x<b\right\}}$

das rechtsseitig offene Intervall.

Für das offene Intervall wird häufig auch ${}(a,b)$ geschrieben. Die Zahlen ${}a$ und ${}b$ heißen die Grenzen des Intervalls, genauer spricht man von oberer und unterer Grenze. Die Bezeichnung linksseitig und rechtsseitig bei den beiden letzten Intervallen (die man auch als halboffen bezeichnet) rühren von der üblichen Repräsentierung der reellen Zahlen als Zahlengerade her, bei der rechts die positiven Zahlen stehen. Zutreffender (also weniger konventionsverhaftet) wäre es von „größerseitig offen“ und „kleinerseitig offen“ zu sprechen. Manchmal werden auch Schreibweisen wie ${}(a,\infty )$ verwendet. Dies bedeutet nicht, dass es in ${}K$ ein Element ${}\infty$ gibt, sondern ist lediglich eine kurze Schreibweise für ${}{\left\{x\in K\mid x>a\right\}}$.

Bemerkung

Ein äquivalenter Zugang zum Begriff des angeordneten Körpers funktioniert so: Man hat einen Körper ${}K$, bei dem eine Teilmenge ${}P\subseteq K$ (die „positive Hälfte“) ausgezeichnet ist mit den folgenden Eigenschaften

1. Entweder ${}x\in P$ oder ${}-x\in P$ oder ${}x=0$.
2. Aus ${}x,y\in P$ folgt ${}x+y\in P$.
3. Aus ${}x,y\in P$ folgt ${}x\cdot y\in P$.

In einem angeordneten Körper erfüllen die positiven Elemente diese Bedingungen. Man kann aber umgekehrt aus einem Körper mit einer solchen positiven Teilmenge einen angeordneten Körper machen, indem man

$x\geq y{\text{ durch }}x=y{\text{ oder }}x-y\in P$

definiert, siehe Aufgabe 6.19.

Der Betrag

Definition (Betrag)

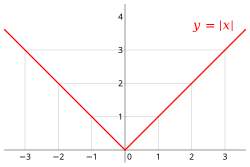
In einem angeordneten Körper ${}K$ ist der Betrag eines Elementes ${}x\in K$ folgendermaßen definiert.

${}\vert {x}\vert ={\begin{cases}x,\,{\text{ falls }}x\geq 0\,,\\-x,\,{\text{ falls }}x<0\,.\end{cases}}\,$

Der Betrag ist also nie negativ und hat nur bei ${}x=0$ den Wert ${}0$, sonst ist er immer positiv. Die Gesamtabbildung

$K\longrightarrow K,\,x\longmapsto \vert {x}\vert ,$

nennt man auch Betragsfunktion. Der Funktionsgraph setzt sich aus zwei Halbgeraden zusammen; eine solche Funktion nennt man auch stückweise linear.

Lemma

Es sei ${}K$ ein angeordneter Körper.

Dann erfüllt die Betragsfunktion

$K\longrightarrow K,\,x\longmapsto \vert {x}\vert ,$

folgende Eigenschaften (dabei seien ${}x,y$ beliebige Elemente in ${}K$).

1. Es ist ${}\vert {x}\vert \geq 0$.
2. Es ist ${}\vert {x}\vert =0$ genau dann, wenn ${}x=0$ ist.
3. Es ist ${}\vert {x}\vert =\vert {y}\vert$ genau dann, wenn ${}x=y$ oder ${}x=-y$ ist.
4. Es ist ${}\vert {y-x}\vert =\vert {x-y}\vert$.
5. Es ist ${}\vert {xy}\vert =\vert {x}\vert \vert {y}\vert$.
6. Für ${}x\neq 0$ ist ${}\vert {x^{-1}}\vert =\vert {x}\vert ^{-1}$.
7. Es ist ${}\vert {x+y}\vert \leq \vert {x}\vert +\vert {y}\vert$ (Dreiecksungleichung für den Betrag).
8. Es ist ${}\vert {x+y}\vert \geq \vert {x}\vert -\vert {y}\vert$.

Beweis

Siehe Aufgabe 6.20.

$\Box$

Bernoulli'sche Ungleichung

In der folgenden Aussage verwenden wir für ein Element ${}z\in K$ in einem Körper und einer natürlichen Zahl ${}n\in \mathbb {N}$ die Schreibweisen

$nz=\underbrace {z+\cdots +z} _{n{\text{-mal}}}{\text{ und }}z^{n}=\underbrace {z{\cdots }z} _{n{\text{-mal}}}.$

Satz (Bernoulli Ungleichung)

Es sei ${}K$ ein angeordneter Körper und ${}n$ eine natürliche Zahl. Dann gilt für jedes ${}x\in K$ mit ${}x\geq -1$ die Abschätzung

${}(1+x)^{n}\geq 1+nx\,.$

Beweis

Wir führen Induktion über ${}n$. Bei ${}n=0$ steht beidseitig ${}1$, sodass die Aussage gilt. Es sei nun die Aussage für ${}n$ bereits bewiesen. Dann ist

${}{\begin{aligned}(1+x)^{n+1}&=(1+x)^{n}(1+x)\\&\geq (1+nx)(1+x)\\&=1+(n+1)x+nx^{2}\\&\geq 1+(n+1)x,\end{aligned}}$

da Quadrate (und positive Vielfache davon) in einem angeordneten Körper nichtnegativ sind.

$\Box$

Archimedisch angeordnete Körper

Wenn man sich wie üblich die reellen Zahlen als Zahlengerade vorstellt, so ist das nächste Axiom selbstverständlich. Es gibt aber auch sehr interessante angeordnete Körper, in denen dieses Axiom nicht gilt; es gilt auch nicht im Rahmen der sogenannten Nichtstandardanalysis. Zur Formulierung dieses Axioms muss man jede natürliche Zahl in einem Körper ${}K$ interpretieren können. Dies geschieht, indem man einer natürlichen Zahl ${}n\in \mathbb {N}$ das Körperelement

${}n_{K}=\underbrace {1_{K}+\cdots +1_{K}} _{n{\text{-mal}}}\,$

zuordnet.

Archimedes (ca. 287 -212 v. C.)

Definition

Es sei ${}K$ ein angeordneter Körper. Dann heißt ${}K$ archimedisch angeordnet, wenn das folgende Archimedische Axiom gilt, d.h. wenn es zu jedem ${}x\in K$ eine natürliche Zahl ${}n$ mit

${}n\geq x\,$

gibt.

Diese Eigenschaft ist für negative Elemente stets erfüllt, für positive Elemente handelt es sich aber um eine echte neue Bedingung, die nicht jeder angeordnete Körper erfüllt. Die rationalen Zahlen und die reellen Zahlen bilden jeweils einen archimedisch angeordneten Körper, ein nicht-archimedisch angeordneter Körper wird in Aufgabe 17.24 besprochen. Einen archimedisch angeordneten Körper kann man sich als eine Zahlengerade vorstellen, auf denen auch die ganzen Zahlen liegen. Mit Zahlengerade wird noch nichts genaues über „Lücken“ oder „Kontinuität“ behauptet.

Lemma

Es sei ${}K$ ein archimedisch angeordneter Körper.

Dann gibt es zu ${}x,y\in K$ mit ${}x>0$ stets ein ${}n\in \mathbb {N}$ mit ${}nx>y$.

Beweis

Wir betrachten ${}y/x$. Aufgrund des Archimedes-Axioms gibt es ein ${}n$ mit ${}n\geq y/x$. Da ${}x$ positiv ist, gilt nach Lemma 6.2  (6) auch ${}nx\geq y$.

$\Box$

Lemma

Es sei ${}K$ ein archimedisch angeordneter Körper. Es sei ${}x>0$.

Dann gibt es eine natürliche Zahl ${}n\in \mathbb {N}$ mit ${}{\frac {1}{n}}\leq x$.

Beweis

Es ist ${}x^{-1}$ eine nach Fakt *****  (1) positive Zahl und daher gibt es eine natürliche Zahl ${}n\in \mathbb {N}$ mit ${}n\geq x^{-1}>0$. Dies ist nach Fakt *****  (4) äquivalent zu

${}{\frac {1}{n}}=n^{-1}\leq {\left(x^{-1}\right)}^{-1}=x\,.$

$\Box$

Im folgenden Lemma verwenden wir, dass man zunächst die ganzen Zahlen ${}\mathbb {Z}$ in einem angeordneten Körper ${}K$ wiederfindet und dass man dann auch die rationalen Zahlen ${}\mathbb {Q}$ in ${}K$ wiederfindet. Die rationale Zahl ${}n/m$ ist als das Element ${}n_{K}\cdot (m_{K})^{-1}$ zu interpretieren, siehe auch Aufgabe 6.17.

Lemma

Es sei ${}K$ ein archimedisch angeordneter Körper.

Dann gibt es zwischen je zwei Elementen ${}x<y$ auch eine rationale Zahl ${}n/k$ (mit ${}n\in \mathbb {Z} ,\,k\in \mathbb {N} _{+}$) mit

${}x<{\frac {n}{k}}<y\,.$

Beweis

Wegen ${}y>x$ ist ${}y-x>0$ und daher gibt es nach Lemma 6.10 ein ${}k\in \mathbb {N}$ mit ${}{\frac {1}{k}}<y-x$. Nach Lemma 6.9 gibt es auch ein ${}n\in \mathbb {N}$ mit

${}n{\frac {1}{k}}>x\,$

und ein ${}n'\in \mathbb {Z} _{-}$ mit

${}n'{\frac {1}{k}}\leq x\,.$

Daher gibt es auch ein ${}n\in \mathbb {Z}$ derart, dass

$n{\frac {1}{k}}>x\,\,{\text{ und }}\,\,(n-1){\frac {1}{k}}\leq x$

ist. Damit ist einerseits

${}x<{\frac {n}{k}}\,$

und andererseits

${}{\frac {n}{k}}={\frac {n-1}{k}}+{\frac {1}{k}}<x+y-x=y\,$

wie gewünscht.

$\Box$

In einem archimedisch angeordneten Körper bilden die ganzzahligen Intervalle ${}[n,n+1[$, ${}n\in \mathbb {Z}$, eine disjunkte Überdeckung. Deshalb ist die folgende Definition sinnvoll.

Definition

Es sei ${}K$ ein archimedisch angeordneter Körper und ${}x\in K$. Die Gaußklammer von ${}x$ ist durch

$\left\lfloor x\right\rfloor =n,{\text{ falls }}x\in [n,n+1[{\text{ und }}n\in \mathbb {Z} ,$

definiert.

Da die Werte der Gaußklammer die ganzen Zahlen sind, kann man die Gaußklammer auch als eine Abbildung ${}K\rightarrow \mathbb {Z}$ auffassen.

Lemma

Es sei ${}K$ ein archimedisch angeordneter Körper und ${}x>1$.

Dann gibt es zu jedem ${}B\in K$ eine natürliche Zahl ${}n\in \mathbb {N}$ mit

${}x^{n}\geq B\,.$

Beweis

Wir schreiben ${}x=1+u$ mit ${}u>0$. Aufgrund von Lemma 6.9 gibt es eine natürliche Zahl ${}n$ mit ${}nu\geq B-1$. Damit gilt unter Verwendung der Bernoulli-Ungleichung die Abschätzung

${}x^{n}=(1+u)^{n}\geq 1+nu\geq 1+B-1=B\,.$

$\Box$

Tupel

In der Definition einer Abbildung sind die Definitionsmenge und die Wertemenge grundsätzlich gleichwichtig. Dennoch gibt es Situationen, wo mal das Hauptgewicht auf der einen oder der anderen Menge liegt. Der allgemeine Abbildungsbegriff deckt eben auch Situationen ab, bei denen man zunächst gar nicht unbedingt an Abbildungen denkt.

Betrachten wir beispielsweise die Potenzmenge einer Menge ${}M$. Jede Teilmenge von ${}M$ kann man mit einer Abbildung von ${}M$ in die zweielementige Menge ${}\{0,1\}$ identifizieren, siehe Aufgabe 1.15. Hier ist also die Wertemenge extrem einfach und die Abbildung repräsentiert an jeder Stelle eine Ja/Nein-Entscheidung.

Andererseits kann man (geordnete) Paare ${}(x,y)$ zu einer Menge ${}M$, also Elemente aus der Produktmenge ${}M\times M$, als eine Abbildung

$f\colon \{1,2\}\longrightarrow M$

ansehen, mit ${}f(1)=x$ und ${}f(2)=y$. Hier identifiziert man also die Abbildung mit der geordneten Aufzählung der Werte. In einer solchen Situation bezeichnet man die Abbildung häufig mit einem Symbol, das sich an den Bezeichnungen für die Elemente aus ${}M$ anlehnt. Wenn man beispielsweise die Elemente aus ${}M$ mit ${}x$ bezeichnet, so schreibt man für ein Paar häufig

${}x=(x_{1},x_{2})\,$

In der Sprache der Abbildungen ist dabei ${}x_{i}$ der Wert der Abbildung ${}x$ an der Stelle ${}i$. Die Schreibweise ${}x_{i}$ (statt ${}x(i)$) suggeriert, dass das Hauptgewicht darauf liegt, was in der Wertemenge ${}M$ passiert, und nicht in der Definitionsmenge.

Definition

Es seien ${}I$ und ${}M$ Mengen. Dann nennt man eine Abbildung

$x\colon I\longrightarrow M,\,i\longmapsto x_{i},$

auch ein ${}I$-Tupel in ${}M$. Bei ${}I=\{1,\ldots ,n\}$ spricht man von einem ${}n$-Tupel in ${}M$.

Die Menge ${}I$ heißt in diesem Zusammenhang auch Indexmenge, ein Element aus der Indexmenge heißt Index. Bei einem ${}I$-Tupel ${}x$ sind die Elemente durch die Indices indiziert. Zu ${}i\in I$ heißt ${}x_{i}$ die ${}i$-te Komponente des Tupels. Ein ${}n$-Tupel schreibt man meist als

$(x_{1},x_{2},\ldots ,x_{n}).$

Bei einer zweielementigen Indexmenge spricht man von einem Paar, bei einer dreielementigen Menge von einem Tripel.

Die Menge aller ${}I$-Tupel wird mit

${}M^{I}=\{f:I\rightarrow M\}=\operatorname {Abb} \,{\left(I,M\right)}\,$

bezeichnet. Bei ${}I=\{1,\ldots ,n\}$ schreibt man auch

$M^{n}=M^{\{1,\ldots ,n\}}=\underbrace {M\times \cdots \times M} _{n{\text{-mal}}}.$

Die reelle Ebene ${}\mathbb {R} ^{2}$ ist also nichts anderes als die Menge der Zweitupel von reellen Zahlen, der reelle Raum ${}\mathbb {R} ^{3}$ besteht aus allen reellen Tripeln.

Bei ${}I=\mathbb {N}$ spricht man von Folgen in ${}M$, worauf wir in aller Ausführlichkeit noch eingehen werden. Eine endliche Indexmenge kann man stets durch eine Menge der Form ${}\{1,\ldots ,n\}$ ersetzen (diesen Vorgang kann man eine Nummerierung der Indexmenge nennen), doch ist das nicht immer sinnvoll. Wenn man z.B. mit einer Indexmenge ${}I=\{1,\ldots ,n\}$ startet und sich dann für gewisse Teilindexmengen ${}J\subseteq I$ interessiert, so ist es natürlich, die von ${}I$ ererbten Bezeichnungen beizubehalten, anstatt ${}J$ mit einer neuen Nummerierung ${}\{1,\ldots ,m\}$ zu versehen. Häufig gibt es für ein bestimmtes Problem „natürliche“ Indexmengen, die (allein schon mnemotechnisch)

einen Teil des strukturellen Gehalts des Problems widerspiegeln. Eine lineare Abbildung vom ${}\mathbb {R} ^{n}$ in den ${}\mathbb {R} ^{m}$ wird z.B. durch eine Matrix mit ${}m$ Zeilen und ${}n$ Spalten beschrieben, also insgesamt mit ${}mn$ Einträgen. Diese Matrixeinträge indiziert man am einfachsten mit einem Doppelindex

$a_{ij},$

wobei der eine Index für den Spaltenindex und der andere für den Zeilenindex steht. Durch eine solche natürliche Bezeichnung ist stets der Bezug klar, und dieser würde völlig verloren gehen, wenn man eine neue Indexmenge der Form ${}\{1,2,\ldots ,mn\}$ einführen würde.

Familien von Mengen

Es können nicht nur Elemente, sondern auch Mengen durch eine Indexmenge indiziert werden. Dann spricht man von einer Mengenfamilie.

Definition

Es sei ${}I$ eine Menge und zu jedem ${}i\in I$ sei eine Menge ${}M_{i}$ gegeben. Eine solche Situation nennt man eine Familie von Mengen

$M_{i}{\text{ , }}i\in I.$

Die Menge ${}I$ heißt dabei die Indexmenge der Mengenfamilie.

Dabei können die Mengen völlig unabhängig voneinander sein, es kann aber auch sein, dass sie alle Teilmengen einer bestimmten Grundmenge sind.

Definition

Es sei ${}M_{i}$, ${}i\in I$, eine Familie von Teilmengen einer Grundmenge ${}G$. Dann heißt

${}\bigcap _{i\in I}M_{i}={\left\{x\in G\mid x\in M_{i}{\text{ für alle }}i\in I\right\}}\,$

der Durchschnitt der Mengen und

${}\bigcup _{i\in I}M_{i}={\left\{x\in G\mid {\text{es gibt ein }}i\in I{\text{ mit }}x\in M_{i}\right\}}\,$

die Vereinigung der Mengen.

Man beachte, dass dabei der Durchschnitt und die Vereinigung auf den All- bzw. den Existenzquantor zurückgeführt wird.

Definition

Es sei ${}I$ eine Menge und zu jedem ${}i\in I$ sei eine Menge ${}M_{i}$ gegeben. Dann nennt man die Menge

${}M=\prod _{i\in I}M_{i}=\{(x_{i})_{i\in I}:\,x_{i}\in M_{i}{\text{ für alle }}i\in I\}\,$

die Produktmenge der ${}M_{i}$.

Sobald eine der beteiligten Mengen ${}M_{i}$ leer ist, ist auch das Produkt leer, da es dann für die ${}i$-te Komponente keinen möglichen Wert gibt. Wenn aber umgekehrt alle Mengen ${}M_{i}$ nicht leer sind, so ist auch ihr Produkt nicht leer, da man für jeden Index ${}i$ dann ein Element ${}x_{i}\in M_{i}$ wählen kann. Bei einem formalen axiomatischen Aufbau der Mengentheorie muss man übrigens fordern, dass dieses Wählen möglich ist. Dies ist der Inhalt des Auswahlaxioms.

Beispiel

Zu ${}n\in \mathbb {N}$ sei

${}M_{n}={\left\{x\in \mathbb {N} \mid x\geq n\right\}}\,$

die Menge aller natürlichen Zahlen, die mindestens so groß wie ${}n$ sind. Diese ist eine durch die natürlichen Zahlen indizierte Familie von Teilmengen von ${}\mathbb {N}$. Es gelten die Inklusionen

$M_{n}\subseteq M_{m}{\text{ für }}n\geq m.$

Der Durchschnitt

$\bigcap _{n\in \mathbb {N} }M_{n}$

ist leer, da es keine natürliche Zahl gibt, die größer/gleich jeder anderen natürlichen Zahl ist.

Beispiel

Zu ${}n\in \mathbb {N} _{+}$ sei

${}\mathbb {N} n={\left\{x\in \mathbb {N} _{+}\mid x{\text{ ist ein Vielfaches von }}n\right\}}\,$

die Menge aller positiven natürlichen Zahlen, die Vielfache von ${}n$ sind. Dies ist eine durch die positiven natürlichen Zahlen indizierte Familie von Teilmengen von ${}\mathbb {N}$. Es gelten die Inklusionen

$\mathbb {N} n\subseteq \mathbb {N} m{\text{ für }}m{\text{ teilt }}n.$

Der Durchschnitt

$\bigcap _{n\in \mathbb {N} _{+}}\mathbb {N} n$

ist leer, da es keine positive natürliche Zahl gibt, die ein Vielfaches von jeder positiven natürlichen Zahl ist (die ${}0$ ist ein solches Vielfaches).

Beispiel

Es sei ${}x$ eine reelle Zahl und es sei ${}x_{n}$ diejenige rationale Zahl, die sich aus allen Vorkommaziffern und den ersten ${}n$ Nachkommaziffern von ${}x$ im Dezimalsystem ergibt. Wir definieren die Intervalle

${}M_{n}=\left[x_{n},x_{n}+{\left({\frac {1}{10}}\right)}^{n}\right]\subset \mathbb {R} \,.$

Dies sind Intervalle der Länge ${}{\left({\frac {1}{10}}\right)}^{n}$ und es ist

${}\{x\}=\bigcap _{n\in \mathbb {N} }M_{n}\,.$

Die Familie ${}M_{n}$, ${}n\in \mathbb {N}$, ist also eine Intervallschachtelung für ${}x$.

Beispiel

Es sei ${}M$ eine Menge. Für ${}n\in \mathbb {N}$ definieren wir rekursiv

$M_{0}=M{\text{ und }}M_{n}={\mathfrak {P}}\,(M_{n-1}){\text{ für }}n\geq 1.$

Man nimmt also jeweils von der Vorgängermenge die Potenzmenge. Ein Element aus dem Produkt

$(x_{n})\in \prod _{n\in \mathbb {N} }M_{n}$

besteht also in der nullten Komponenten aus einem Element aus ${}M$, in der ersten Komponenten aus einer Teilmenge von ${}M$, in der zweiten Komponenten aus einer Menge von Teilmengen von ${}M$ usw. Zwischen den einzelnen Mengen aus der Familie besteht keine Inklusionsbeziehung.

Fußnoten

<< | Kurs:Mathematik (Osnabrück 2009-2011)/Teil I | >> PDF-Version dieser Vorlesung Arbeitsblatt zur Vorlesung (PDF)