Kurs:Grundkurs Mathematik (Osnabrück 2018-2019)/Teil II/Vorlesung 40
Wir besprechen nun mit Hilfe von Äquivalenzrelationen, Äquivalenzklassen und Quotientenmengen erneut, wie man aus den natürlichen Zahlen die ganzen Zahlen und wie man aus den ganzen Zahlen die rationalen Zahlen konstruieren kann. Dieser Zugang ist zwar abstrakter, aber konzeptionell klarer, allgemeiner und systematischer. In einigen Wochen werden wir die reellen Zahlen aus den rationalen Zahlen ebenfalls mittels Äquivalenzrelationen definieren.
- Die Konstruktion der ganzen Zahlen
Die ganzen Zahlen haben wir in der 18. Vorlesung einfach als die disjunkte Vereinigung von natürlichen und negativen Zahlen eingeführt und dann nach und nach die Verknüpfungen und die Ordnungsrelation festgelegt und die wichtigsten Eigenschaften bewiesen. Dabei hatten wir es häufig, beispielsweise beim Nachweis der Assoziativität für die Multiplikation, mit einer Vielzahl von Fallunterscheidungen zu tun, die wir im Einzelnen gar nicht alle ausgeführt haben.
Es sei die Menge der natürlichen Zahlen und die Produktmenge mit der komponentenweisen Addition. Wir erklären auf eine Relation durch
Es wird hier also über Kreuz addiert, um diese Relation zu erhalten. Diese Relation ist bei genau dann erfüllt, wenn es ein (nämlich die natürliche Zahl ) mit
gibt und bei genau dann erfüllt, wenn es ein (nämlich ) mit
gibt. So oder so kann man sagen, dass die Paare und zueinander äquivalent sind, wenn sie sich um ein Diagonalelement, also um ein Paar, wo beide Komponenten übereinstimmen, unterscheiden. Diese Relation ist eine Äquivalenzrelation auf . Das ist von der soeben etablierten Interpretation als „gleichdiagonalig“ her klar, kann aber auch direkt gezeigt werden:
- Wegen ist , die Relation ist also reflexiv.
- Die Symmetrie folgt daraus, dass aus sofort folgt.
- Zum Nachweis der Transitivität sei
und ,
also
und
.
Dann ist
Aufgrund der Abziehregel ist dann
und dies bedeutet .
Passende Interpretationen für die Paare mit dieser Äquivalenzrelation sind beispielsweise:
- Das Paar repräsentiert das Ergebnis eines Fußballspieles, wobei die Toranzahl der Heimmannschaft und die Toranzahl der Gastmannschaft repräsentiert. Zwei Spiele gelten dann als äquivalent, wenn die „gerichtete Differenz“ gleich ist. Ein wird als äquivalent zu einem betrachtet, wenn beide Mannschaften ein weiteres Tor schießen, ändert sich zwar das Paar, aber nicht die Äquivalenzklasse. Die Äquivalenzklassen kann man charakterisieren als Unentschieden, mit einem Tor Vorsprung gewonnen, mit zwei Toren Vorsprung gewonnen, mit drei Toren Vorsprung gewonnen, ... , mit einem Tor Unterschied verloren, mit zwei Toren Unterschied verloren, mit drei Toren Unterschied verloren, ....
- Das Paar repräsentiert das Alter eines menschlichen Paares, wobei für das Alter der Frau und für das Alter des Mannes steht. Die Äquivalenzklasse ist durch den gerichteten Altersunterschied (also den Altersunterschied mit der zusätzlichen Information, wer älter ist)
festgelegt. Diese Beziehung ändert sich im Laufe des Lebens nicht, da beide gleichermaßen älter werden.
- Das Paar kann die Einnahmen und Ausgaben eines Haushaltes in einem Monat beschreiben, wobei die erste Stelle die Einnahmen und die zweite Stelle die Ausgaben repräsentieren möge. Zwei Haushalte
(oder Monate) sind dann äquivalent, wenn sie den gleichen Überschuss oder das gleiche Defizit erwirtschaftet haben. Wenn Einnahmen und Ausgaben gleichermaßen steigen oder fallen, ändert sich an dieser Gesamtbewertung nichts.
- Man kann das Paar als eine Schrittfolge aus Schritten nach rechts und Schritten nach links ansehen. Im Paar selbst wird die Anzahl der Schritte in die beiden Richtungen notiert, für die Äquivalenzrelation schaut man nur das Endergebnis des Bewegungsvorganges an.
Wenn man als ein quadratisches Gitter anordnet (das ist ein „diskretes Koordinatensystem“), so sind die Äquivalenzklassen durch die Punkte auf einer zur Diagonalen parallelen „diskreten Geraden“ gegeben. Die Punkte mit sind äquivalent zu , sie haben also einen Repräsentanten, bei dem die zweite Komponente ist. Die Punkte mit sind äquivalent zu , sie haben also einen Repräsentanten, bei dem die erste Komponente ist. Die Punkte sind zu äquivalent. Den Repräsentanten einer Äquivalenzklasse, bei dem mindestens eine Komponente ist, nennen wir den Standardvertreter dieser Äquivalenzklasse. Die Standardvertreter sind die diskreten Punkte des begrenzenden Viertelkreuzes; zu einem Punkt ergibt sich der Standardvertreter, indem man parallel zur Diagonalen in Richtung der Halbachsen wandert, bis man auf einer der Halbachsen landet. Zwei Punkte sind genau dann äquivalent, wenn sie den gleichen Standardvertreter besitzen.
Wir bezeichnen nun die Quotientenmenge, also die Menge der Äquivalenzklassen unter dieser Äquivalenzrelation, als Menge der ganzen Zahlen und bezeichnen sie mit . Wir sprechen vom Äquivalenzklassenmodell oder Paarmodell für die ganzen Zahlen. Diese Quotientenmenge ist die Menge der zur Diagonalen parallelen diskreten Geraden, bei der kanonischen Projektion wird jedes Paar auf die Gerade abgebildet, auf der es liegt. Jede ganze Zahl hat genau einen Standardvertreter der Form mit , der Form oder der Form mit . Eine natürliche Zahl fassen wir in diesem Modell als die ganze Zahl auf, und negative Zahlen werden als spezielle Äquivalenzklassen eingeführt.
Wir wollen nun zwei ganze Zahlen, also zwei solche Äquivalenzklassen und , miteinander „addieren“, also eine Verknüpfung auf einführen. Ein Ansatz, der sich durch den Zugang über Äquivalenzklassen eröffnet, ist es, auf der Menge der Paare die Addition zu nehmen und zu versuchen, diese Addition auf die Äquivalenzklassen zu übertragen. Die komponentenweise Addition auf , also die Verknüpfung
ist recht einfach und insbesondere ist diese Verknüpfung kommutativ, assoziativ und ist das neutrale Element. Diese Addition hat in den oben angegebenen Beispielen eine sinnvolle Interpretation, wie wenn man die Ergebnisse von zwei Fußballspielen miteinander addiert (Hin- und Rückspiel, allerdings muss man die Reihenfolge beibehalten) oder das Haushaltsgeschehen von mehreren Monaten addiert.
Durch die Festlegung
erhält man auf (dem Äquivalenzklassenmodell von) eine Verknüpfung, die kommutativ und assoziativ ist und die als neutrales Element besitzt. Darüber hinaus besitzt jedes Element ein inverses Element, und zwar sind und invers zueinander.
Wir müssen zuerst die Wohldefiniertheit überprüfen, da die Verknüpfung unter Bezug auf Repräsentanten erklärt wird und daher nicht von vornherein klar ist, dass unterschiedliche Repräsentanten zum gleichen Ergebnis (zur gleichen Äquivalenzklasse) führen. Zu und muss man überprüfen, dass
und damit gilt. Die beiden Voraussetzungen bedeuten ausgeschrieben und . Damit ist durch Addition der beiden Gleichungen
was die Äquivalenz bedeutet. Die kanonische Abbildung
verträgt sich nach Konstruktion mit der Addition auf der Produktmenge und der soeben etablierten Addition auf , es ist also
für alle . In einer solchen Situation übertragen sich wegen der Surjektivität der kanonischen Abbildung Rechengesetze von direkt auf die Quotientenmenge. Für das Assoziativgesetz beispielsweise betrachten wir Elemente . Es gibt mit , , . Somit ist
Der Nachweis der Kommutativität und dass das neutrale Element der Verknüpfung ist, verläuft ähnlich einfach. Wegen
ist in der Tat das inverse Element zu .
Durch die Festlegung
erhält man auf (dem Äquivalenzklassenmodell von) eine Verknüpfung, die kommutativ und assoziativ ist und die als neutrales Element besitzt.
Beweis
Das Äquivalenzklassenmodell von ist mit der Addition
der Multiplikation
dem Nullelement und dem Einselement
ein kommutativer Ring.
Aufgrund von Lemma 40.1 und Lemma 40.2 müssen wir nur noch das Distributivgesetz überprüfen. Dieses ist wegen
erfüllt.
Das Äquivalenzklassenmodell von ist mit der Addition
der Multiplikation
dem Nullelement , dem Einselement und der durch
falls
definierten Ordnung
ein angeordneter Ring.
Nach Satz 40.3 ist ein kommutativer Ring und nach Lemma 40.4 ist eine totale Ordnung. Wir müssen also lediglich noch die Verträglichkeit der Ordnung mit der Addition und der Multiplikation überprüfen. Sei
also , und beliebig. Dann ist auch
also
Wenn und ist, so ist und . Mit Aufgabe 10.30 ergibt sich
was
bedeutet.
Die natürlichen Zahlen sind über die Zuordnung
in den ganzen Zahlen enthalten. Diese Zuordnung ist mit der Addition, der Multiplikation und der Ordnung verträglich, siehe Aufgabe 40.7. Statt schreibt man einfach . Die ganzen Zahlen, die durch mit repräsentiert werden, heißen negative Zahlen. Statt schreibt man einfach .
In den Aufgaben wird gezeigt, dass das Paarmodell für mit dem im ersten Semester eingeführten Modell übereinstimmt.
- Die Konstruktion der rationalen Zahlen
Wir wollen ausgehend von der Menge der ganzen Zahlen , die einen kommutativen Ring bildet, die Menge der rationalen Zahlen konstruieren. Wir gehen dabei ähnlich wie bei der Konstruktion der ganzen Zahlen aus den natürlichen Zahlen vor, indem wir auf einer „zu großen“ Menge eine Äquivalenzrelation einführen, sodass die Quotientenmenge ein Modell für die rationalen Zahlen ist. Die Konstruktion und die Beweise sind nicht wesentlich verschieden von den in der 23. Vorlesung durchgeführten, als wir die Sprache der Äquivalenzrelationen noch nicht zur Verfügung hatten.
Wir starten mit der Produktmenge
Zur Orientierung sei schon jetzt gesagt, dass das Paar später den Bruch repräsentieren soll.
Man kann sich vorstellen, dass in die erste Zahl eine Anzahl an Kuchen und die zweite Zahl eine Anzahl an Personen bedeutet, oder die Anzahl der Frauen und die Anzahl der Männer auf einer Party, oder irgendein Paar, das einen proportionalen Zusammenhang repräsentiert.
Auf wollen wir eine Äquivalenzrelation definieren, wobei zwei Paare als äquivalent gelten sollen, wenn sie „den gleichen Bruch“ repräsentieren (den es noch nicht gibt). Wir definieren
Diese Relation wird also unter Bezug auf die Gleichheit in erklärt. Es handelt sich dabei um eine Äquivalenzrelation, wie man direkt nachrechnen kann, siehe Aufgabe 40.5. Insbesondere sind und für zueinander äquivalent.
Es ist hilfreich, sich diese Situation zu veranschaulichen, indem man die diskrete obere Halbebene[1]
betrachtet. Ein Paar ist dann ein Gitterpunkt, wobei wir uns die ganzen Zahlen als die Punkte(wo also die zweite Komponente konstant ist.) bezeichnen wir mit . Ein jeder Punkt definiert eine eindeutige Gerade, die durch diesen Punkt und durch den Nullpunkt verläuft. In dieser geometrischen Interpretation sind zwei Punkte und genau dann äquivalent, wenn sie die gleiche Gerade definieren, und dies ist genau dann der Fall, wenn ihre „Steigungen“ übereinstimmen. Zwei Punkte liegen ja genau dann auf der gleichen Geraden, wenn sie, wenn man durch Streckung ihre zweite Koordinate zur Übereinstimmung bringt, dann auch die erste Koordinate übereinstimmt. Wenn man den ersten Punkt mit streckt (multipliziert) und den zweiten Punkt mit , so erhält man die beiden Punkte und , und die Gleichheit vorne war die Definition für die Relation. Die Äquivalenzklassen sind die „diskreten Geraden“ durch den Nullpunkt und einen weiteren Gitterpunkt.
Auch die Identifizierungsabbildung zu dieser Äquivalenzrelation kann man sich gut vorstellen. Der Schnittpunkt der durch einen Punkt und dem Nullpunkt definierten Geraden mit der Zahlengeraden ist ein Punkt, der dem Bruch entspricht (die Steigung der Geraden ist aber ).
Die Quotientenmenge unter dieser Äquivalenzrelation nennen wir und sprechen vom Äquivalenzklassenmodell für . Für die Elemente in schreiben wir vorläufig noch . Wir wollen nun auf eine Addition und eine Multiplikation definieren.
Durch die Festlegung
erhält man auf (dem Äquivalenzklassenmodell von) eine Verknüpfung, die kommutativ und assoziativ ist und die als neutrales Element besitzt. Darüber hinaus besitzt jedes Element ein inverses Element, und zwar sind und invers zueinander.
Zum Nachweis der Wohldefiniertheit seien und , also und . Dann ist
und somit
Die Kommutativität und die Eigenschaft, dass das neutrale Element der Verknüpfung ist, folgen unmittelbar aus der Definition. Zum Beweis der Assoziativität seien gegeben. Es ist dann
Ferner ist
Durch die Festlegung
erhält man auf (dem Äquivalenzklassenmodell von) eine Verknüpfung, die kommutativ und assoziativ ist und die als neutrales Element besitzt. Darüber hinaus besitzt jedes Element ein inverses Element, und zwar sind bei die Klassen und und bei die Klassen und invers zueinander.
Beweis
Das Äquivalenzklassenmodell von ist mit der Addition
der Multiplikation
dem Nullelement und dem Einselement
ein Körper.
Dies folgt aus Lemma 40.6 und aus Lemma 40.7, es ist somit lediglich noch das Distributivgesetz zu begründen. Dies ergibt sich aus
Durch die Festlegung , falls ,
erhält man auf (dem Äquivalenzklassenmodell von) eine totale Ordnung.
Beweis
Das Äquivalenzklassenmodell von ist mit der Addition
der Multiplikation
dem Nullelement , dem Einselement und der durch
falls
definierten Ordnung
ein angeordneter Körper.
Dies folgt aus Satz 40.8 und Lemma 40.9, es bleibt nur noch die Verträglichkeit der Ordnung mit den Verknüpfungen zu zeigen. Sei
also , und beliebig. Wegen ist dann auch und somit
Wenn und ist, so sind positiv und dann ist auch positiv, also
Die ganzen Zahlen sind über die Zuordnung
in den rationalen Zahlen enthalten. Diese Zuordnung ist mit der Addition, der Multiplikation und der Ordnung verträglich, siehe Aufgabe 40.14. Für die Äquivalenzklasse schreibt man abkürzend .
- Fußnoten
- ↑ Man könnte auch nehmen.
| << | Kurs:Grundkurs Mathematik (Osnabrück 2018-2019)/Teil II | >> |
|---|




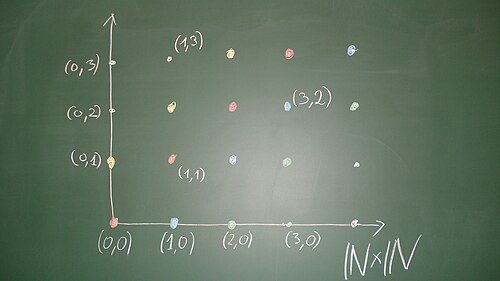








































![{\displaystyle {}[(a,b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad856e5411d0b9ea10ddb04a48932aef19892e7a)
![{\displaystyle {}[(c,d)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b865712c6f9654641f6315839d7fb250d5ed6fa1)



![{\displaystyle {}[(a,b)]+[(c,d)]:=[(a+c,b+d)]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df3c8ae9fedcdfe86d6be396243b2aaa93a5465d)
![{\displaystyle {}[(0,0)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/475a6889495e16a90a7bddd389ad803ee5e078f9)
![{\displaystyle {}[(b,a)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7257885d4524a38fea17a5ad720d33f256cdeaf8)



![{\displaystyle {}[(a+c,b+d)]=[(a'+c',b'+d')]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b9bc368eabf53b7c89081c97a70ea09b665f4fb)



![{\displaystyle q\colon \mathbb {N} \times \mathbb {N} \longrightarrow \mathbb {Z} ,\,(a,b)\longmapsto [(a,b)],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d579ea0ed3a15555fc962cce8c7abecb628a9577)








![{\displaystyle {}[(a,b)]+[(b,a)]=[(a+b,a+b)]=[(0,0)]=0\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30f5374e76e9009d2e2dbd60105b4efe5b036407)

![{\displaystyle {}[(a,b)]\cdot [(c,d)]:=[(ac+bd,ad+bc)]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/271e150f46d092c8a4e0ae63c57aeb711ce6f96d)
![{\displaystyle {}[(1,0)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/729d0600c281952f3efa4039a3bab1a6d0c9833c)
![{\displaystyle {}[(a,b)]+[(c,d)]:=[(a+c,b+d)]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26a52d48bd8d6752f000b989c01ac00bcf01a57c)
![{\displaystyle {}[(a,b)]\cdot [(c,d)]:=[(ac+bd,ad+bc)]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b51e69acf3691a66a51c3e1ceab6b3409966341)
![{\displaystyle {}{\begin{aligned}\,[(a,b)]{\left([(c,d)]+[(e,f)]\right)}&=[(a,b)][(c+e,d+f)]\\&=[(ac+ae+bd+bf,ad+af+bc+be)]\\&=[(ac+bd,ad+bc)]+[(ae+bf,af+be)]\\&=[(a,b)][(c,d)]+[(a,b)][(e,f)]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67e7270a328cd2dd219470b02b9b5b37d5c40df3)
![{\displaystyle {}[(a,b)]\geq [(c,d)]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2391d3d11caaf252146ce25295282921cd03a980)



![{\displaystyle {}[(e,f)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/950de1f8b81cd13973e091bc0624d31c8b02ec5b)

![{\displaystyle {}[(a,b)]+[(e,f)]=[(a+e,b+f)]\geq [(c+e,d+f)]=[(c,d)]+[(e,f)]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fb89e90d55c6ffb32049a8b7957801613ade863)
![{\displaystyle {}[(a,b)]\geq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31a6b964ca907a4cac05f73b2f3c514df5e6621f)
![{\displaystyle {}[(c,d)]\geq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f31586de78745b4a1bd461ab37f6fe9e1100600)


![{\displaystyle {}[(a,b)]\cdot [(c,d)]=[(ac+bd,ad+bc)]\geq 0\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e24997a1efecaea2c8d611c80994c486c8d0a8df)
![{\displaystyle \mathbb {N} \longrightarrow \mathbb {Z} ,\,n\longmapsto [(n,0)],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df42efcb5d068e5db603918e70ac6e888c3dc981)



















![{\displaystyle {}[(a,b)]+[(c,d)]:=[(ad+bc,bd)]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10a5b68f3231d9d43b6c4a425e3f8e104e9ff3fd)
![{\displaystyle {}[(0,1)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1cbcfba51167f69412ad00f1d9f60283d0c1c219)
![{\displaystyle {}[(-a,b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb5fc95544e383aaaa75c29f2bd3e4cc96b40ae6)
![{\displaystyle {}[(a,b)]=[(a',b')]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8209f45a1f6a06ecfc9208e0b7f0003b817107b7)
![{\displaystyle {}[(c,d)]=[(c',d')]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7db12e4064519838da28e989dc1d3aa34d4b15e5)



![{\displaystyle {}[(ad+bc,bd)]=[(a'd'+b'c',b'd')]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc8434deeb1f3314b95277add9dea42a78fd17bc)
![{\displaystyle {}[(a,b)],[(c,d)],[(e,f)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0f812b3de2f2439c6e1a9894ec88c850b19519c)
![{\displaystyle {}{\begin{aligned}\ [(a,b)]+{\left([(c,d)]+[(e,f)]\right)}&=[(a,b)]+[(cf+de,df)]\\&=[(bcf+bde+adf,bdf)]\\&=[(ad+bc,bd)]+[(e,f)]\\&={\left([(a,b)]+[(c,d)]\right)}+[(e,f)].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a96564424670b9263b1ac05aa5032c2e7f37d647)
![{\displaystyle {}[(a,b)]+[(-a,b)]=[ab-ab,b^{2}]=[(0,b^{2})]=[(0,1)]=0\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a5782492d482f47a685841174e7e97798e19e48)
![{\displaystyle {}[(a,b)]\cdot [(c,d)]:=[(ac,bd)]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3127bd5b687c7bca0cd320ad7b490ad21642c4cb)
![{\displaystyle {}[(1,1)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20a4684316706eb5005e009008481ec58079c359)



![{\displaystyle {}[(-b,-a)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84b29d3ae234a512f754d83e1f162e573ceacc47)
![{\displaystyle {}[(a,b)]+[(c,d)]:=[(ad+bc,bd)]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/945cd640953fcab7d25b9e55833fd9ba6d90946c)
![{\displaystyle {}[(a,b)]\cdot [(c,d)]:=[(ac,bd)]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8340b33dcc2b5a621bcaf9be3996c8311b1ef2e)
![{\displaystyle {}{\begin{aligned}\,[(a,b)]{\left([(c,d)]+[(e,f)]\right)}&=[(a,b)][(cf+de,df)]\\&=[(acf+ade,bdf)]\\&=[(acf,bdf)]+[(ade,bdf)]\\&=[(ac,bd)]+[(ae,bf)]\\&=[(a,b)][(c,d)]+[(a,b)][(e,f)].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41f4d4c53e656f412f7f8c743467f7b43049be5b)
![{\displaystyle {}[(a,b)]\geq [(c,d)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67b01e6fa6be8d7d03538cb576d108b582fa43fe)




![{\displaystyle {}{\begin{aligned}\,[(a,b)]+[(e,f)]&=[(af+be,bf)]\\&=[(adf+bde,bdf)]\\&\geq [(bcf+bde,bdf)]\\&=[(cf+de,df)]\\&=[(c,d)]+[(e,f)].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd6b12dc1c70b77480a7e369e6a845987eb0c4cd)


![{\displaystyle {}[(a,b)][(c,d)]=[ac,bd]\geq 0\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9f572004cba1ea9b07ac97dd67c2e4a31ab809f)
![{\displaystyle \mathbb {Z} \longrightarrow \mathbb {Q} ,\,n\longmapsto [(n,1)],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48fa2d6f2edf98cc1f51f9283cc38daee5d5332d)

