Kurs:Körper- und Galoistheorie (Osnabrück 2018-2019)/Vorlesung 25

Die Quadratur des Rechtecks

Die Spirale des Theodorus. In dieser Weise kann man alle Quadratwurzeln von natürlichen Zahlen konstruieren.

Korollar

Es sei ein Rechteck in der Ebene gegeben.

Dann lässt sich mit Zirkel und Lineal ein flächengleiches Quadrat konstruieren.

Beweis

Die Längen der Rechteckseiten seien ${}a$ und ${}b$. Wir wählen einen Eckpunkt des Rechtecks als Nullpunkt und verwenden die Geraden durch die anliegenden Rechteckseiten als Koordinatenachsen. Wir wählen willkürlich einen Punkt ${}1$ (${}\neq 0$) auf einer der Achsen und schlagen einen Kreis um den Nullpunkt durch den Eckpunkt auf der anderen Achse, sodass beide Seitenlängen auf der mit ${}0$ und ${}1$ markierten Achse liegen. Darauf führen wir die Multiplikation ${}ab$ nach Lemma 24.8 durch. Aus diesem Produkt zieht man nun gemäß Lemma 24.10 die Quadratwurzel und erhält somit ${}{\sqrt {ab}}$. Mit dieser Streckenlänge konstruiert man ein Quadrat, dessen Flächeninhalt gleich dem Flächeninhalt des vorgegebenen Rechtecks ist.

$\Box$

Man beachte, dass im Beweis der vorstehenden Aussage die Zahl ${}ab$ (also der Punkt auf der Achse) von der Wahl der ${}1$ abhängt, nicht aber ${}{\sqrt {ab}}$ und damit natürlich auch nicht die Seitenlänge des konstruierten Quadrats.

Konstruierbare und algebraische Zahlen

Wir wollen nun die konstruierbaren Zahlen algebraisch mittels quadratischer Körpererweiterungen charakterisieren. Unter einer reell-quadratischen Körpererweiterung eines Körpers ${}K\subseteq \mathbb {R}$ verstehen wir eine quadratische Körpererweiterung ${}K\subseteq K'$ mit ${}K'\subseteq \mathbb {R}$, die sich also innerhalb der reellen Zahlen abspielt. Eine solche Körpererweiterung ist immer durch die Adjunktion einer Quadratwurzel einer positiven reellen Zahl ${}{\sqrt {c}}$ mit ${}c\in K$, ${}{\sqrt {c}}\notin K$ gegeben. Es gilt die Isomorphie

${}K[{\sqrt {c}}]\cong K[X]/{\left(X^{2}-c\right)}\,.$

Lemma

Es sei ${}K\subseteq \mathbb {R}$ ein Körper. Es sei ${}P\in {\mathbb {C} }$ ein Punkt, der sich aus ${}K^{2}=K+K{\mathrm {i} }$ in einem Schritt konstruieren lässt.

Dann liegen die Koordinaten von ${}P$ in einer reell-quadratischen Körpererweiterung von ${}K$.

Beweis

Wir gehen die drei Möglichkeiten durch, einen Punkt aus ${}K^{2}$ in einem Schritt zu konstruieren. Es sei ${}P$ der Schnittpunkt von zwei verschiedenen Geraden ${}G_{1}$ und ${}G_{2}$, die über ${}K$ definiert sind. Es sei also ${}G_{1}={\left\{(x,y)\mid a_{1}x+b_{1}y+c_{1}=0\right\}}$ und ${}G_{2}={\left\{(x,y)\mid a_{2}x+b_{2}d+c_{2}=0\right\}}$ mit ${}a_{1},b_{1},c_{1},a_{2},b_{2},c_{2}\in K$. Dann gehört der Schnittpunkt zu ${}K^{2}$ und seine Koordinaten gehören zu ${}K$.
Es sei ${}G$ eine über ${}K$ definierte Gerade und ${}C$ ein über ${}K$ definierter Kreis. Dann ist ${}G={\left\{(x,y)\mid ax+by+c=0\right\}}$ und ${}C={\left\{(x,y)\mid (x-r)^{2}+(y-s)^{2}=d\right\}}$ mit ${}a,b,c,r,s,d\in K$. Wir können annehmen, dass ${}b\neq 0$ ist, sodass die Geradengleichung auf die Form ${}y=ux+v$ gebracht werden kann. Einsetzen von dieser Gleichung in die Kreisgleichung ergibt eine quadratische Gleichung für ${}x$ über ${}K$. Die reellen Koordinaten der (eventuell komplexen) Lösungen davon liegen in einer quadratischen Erweiterung von ${}K$. Das gilt dann auch für die zugehörigen Lösungen für ${}y$.
Es seien nun ${}C_{1}$ und ${}C_{2}$ zwei über ${}K$ definierte verschiedene Kreise. Es seien ${}C_{1}={\left\{(x,y)\mid (x-r_{1})^{2}+(y-s_{1})^{2}-a_{1}=0\right\}}$ und ${}C_{2}={\left\{(x,y)\mid (x-r_{2})^{2}+(y-s_{2})^{2}-a_{2}=0\right\}}$ die Kreisgleichungen. Ein Schnittpunkt der beiden Kreise muss auch jede Linearkombination der beiden Gleichungen erfüllen. Wir betrachten die Differenz der beiden Gleichungen, die die Gestalt

${}x(-2r_{1}+2r_{2})+r_{1}^{2}-r_{2}^{2}+y(-2s_{1}+2s_{2})+s_{1}^{2}-s_{2}^{2}-a_{1}+a_{2}=0\,$

besitzt. D.h. dies ist eine Geradengleichung, und die Schnittpunkte der beiden Kreise stimmen mit den Schnittpunkten eines Kreises mit dieser Geraden überein. Wir sind also wieder im zweiten Fall.

$\Box$

Beispiel

Wir betrachten die beiden Kreise mit den Kreisgleichungen

$x^{2}+y^{2}=1{\text{ und }}(x-2)^{2}+y^{2}=3.$

Die Differenz der beiden Gleichungen ist

${}x^{2}-(x-2)^{2}+2=0\,$

bzw.

$4x=2{\text{ und somit }}x={\frac {1}{2}}.$

Die Schnittpunkte der beiden Kreise müssen also auch auf der durch ${}x={\frac {1}{2}}$ gegebenen Geraden liegen. Setzt man diese Geradenbedingung in die erste Kreisgleichung ein, so erhält man

${}y^{2}=1-x^{2}=1-{\frac {1}{4}}={\frac {3}{4}}\,,$

also

${}y=\pm {\frac {\sqrt {3}}{2}}\,.$

Satz

Es sei ${}P\in {\mathbb {C} }$ eine komplexe Zahl. Dann ist ${}P$ eine konstruierbare Zahl genau dann,

wenn es eine Kette von reell-quadratischen Körpererweiterungen

${}\mathbb {Q} \subset K_{1}\subset K_{2}\subset \ldots \subset K_{n}\,$

derart ist, dass die Koordinaten von ${}P$ zu ${}K_{n}$ gehören.

Beweis

Es sei ${}P\in {\mathbb {C} }$ eine konstruierbare komplexe Zahl. D.h. es gibt eine Folge von Punkten ${}P_{1},\ldots ,P_{n}=P$ derart, dass ${}P_{i+1}$ aus den Vorgängerpunkten ${}\{0,1,P_{1},\ldots ,P_{i}\}$ in einem Schritt konstruierbar ist. Es sei ${}P_{i}=\left(a_{i},\,b_{i}\right)$ und es sei

${}K_{i}=\mathbb {Q} (a_{1},b_{1},\ldots ,a_{i},b_{i})\,$

der von den Koordinaten der Punkte erzeugte Unterkörper von ${}\mathbb {R}$. Nach Lemma 25.2 liegt ${}K_{i+1}$ in einer reell-quadratischen Körpererweiterung von ${}K_{i}$ (und zwar ist ${}K_{i+1}=K_{i}$ oder ${}K_{i+1}$ ist eine reell-quadratische Körpererweiterung von ${}K_{i}$). Die Koordinaten von ${}P$ liegen also in ${}K_{n}$, und ${}K_{n}$ ist das Endglied in einer Folge von quadratischen Körpererweiterungen von ${}\mathbb {Q}$.
Es sei umgekehrt angenommen, dass die Koordinaten eines Punktes ${}P=(a,b)$ in einer Kette von reell-quadratischen Körpererweiterungen von ${}\mathbb {Q}$ liegen. Wir zeigen durch Induktion über die Länge der Körperkette, dass die Zahlen in einer solchen Kette aus quadratischen Körpererweiterungen konstruierbar sind. Bei ${}n=0$ ist ${}K_{0}=\mathbb {Q}$, und diese Zahlen sind konstruierbar. Es sei also schon gezeigt, dass alle Zahlen aus ${}K_{n}$ konstruierbar sind, und sei ${}K_{n}\subset K_{n+1}$ eine reell-quadratische Körpererweiterung. Nach Lemma 2.7 ist ${}K_{n+1}=K_{n}[{\sqrt {c}}]$ mit einer positiven reellen Zahl ${}c\in K_{n}$. Nach Induktionsvoraussetzung ist ${}c$ konstruierbar und nach Lemma 24.10 ist ${}{\sqrt {c}}$ konstruierbar. Daher ist auch jede Zahl ${}u+v{\sqrt {c}}$ mit ${}u,v\in K_{n}$, konstruierbar. Damit sind die Koordinaten von ${}P$ konstruierbar und somit ist nach Lemma 24.7 auch ${}P$ selbst konstruierbar.

$\Box$

Wir werden in der nächsten Vorlesung zeigen, dass eine komplex-algebraische Zahl ${}z$ genau dann konstruierbar ist, wenn der Grad des Zerfällungskörpers des Minimalpolynoms von ${}z$ eine Potenz von ${}2$ ist. Für viele Anwendungen sind allerdings schon die oben vorgestellte Charakterisierung und die folgenden Korollare ausreichend.

Korollar

Eine mit Zirkel und Lineal konstruierbare Zahl

ist algebraisch.

Beweis

Dies folgt direkt aus Satz 25.4, aus Satz 2.8 und aus Satz 10.4.

$\Box$

Korollar

Es sei ${}z\in {\mathbb {C} }$ eine konstruierbare Zahl.

Dann ist der Grad des Minimalpolynoms von ${}z$ eine Potenz von zwei.

Beweis

Die Koordinaten der konstruierbaren Zahl ${}z$ liegen nach Satz 25.4 in einer Folge von reell-quadratischen Körpererweiterungen

${}\mathbb {Q} \subset K_{1}\subset K_{2}\subset \ldots \subset K_{n}\,.$

Diese Kette kann man um die komplex-quadratische Körpererweiterung ${}K_{n}\subset K_{n}[{\mathrm {i} }]=L$ ergänzen mit ${}z\in L$. Nach der Gradformel ist der Grad von ${}L$ über ${}\mathbb {Q}$ gleich ${}2^{n+1}$. Dabei ist ${}\mathbb {Q} (z)=\mathbb {Q} [z]\subseteq L$ ein Unterkörper und daher ist, wieder nach der Gradformel, der Grad von ${}\mathbb {Q} [z]$ über ${}\mathbb {Q}$ ein Teiler von ${}2^{n+1}$, also selbst eine Potenz von ${}2$.

$\Box$

Das Delische Problem

Die Bewohner der Insel Delos befragten während einer Pestepidemie 430 v. Chr. das Orakel von Delphi. Sie wurden aufgefordert, den würfelförmigen Altar des Apollon zu verdoppeln.

Wir kommen zur ersten Konsequenz von unserer systematischen Untersuchung der konstruierbaren Zahlen für die klassischen Konstruktionsprobleme.

Korollar

Die Würfelverdopplung mit Zirkel und Lineal ist nicht möglich.

Beweis

Wir betrachten einen Würfel mit der Kantenlänge ${}1$ und dem Volumen ${}1$. Die Konstruktion eines Würfels mit dem doppelten Volumen würde bedeuten, dass man die neue Kantenlänge, also ${}2^{1/3}$ mit Zirkel und Lineal konstruieren könnte. Das Minimalpolynom von ${}2^{1/3}$ ist ${}X^{3}-2$, da dieses offenbar ${}2^{1/3}$ annulliert und nach Satz 17.9 irreduzibel ist. Nach Korollar 25.6 ist ${}2^{1/3}$ nicht konstruierbar, da ${}3$ keine Zweierpotenz ist.

$\Box$

Die Quadratur des Kreises

Satz

Es ist nicht möglich, zu einem vorgegebenen Kreis ein flächengleiches Quadrat mit Zirkel und Lineal zu konstruieren.

Beweis

Wenn es ein Konstruktionsverfahren gäbe, so könnte man insbesondere den Einheitskreis mit dem Radius ${}1$ quadrieren, d.h. man könnte ein Quadrat mit der Seitenlänge ${}{\sqrt {\pi }}$ mit Zirkel und Lineal konstruieren. Nach Korollar 25.5 muss aber eine konstruierbare Zahl algebraisch sein. Nach dem Satz von Lindemann ist aber ${}\pi$ und damit auch ${}{\sqrt {\pi }}$ transzendent.

$\Box$

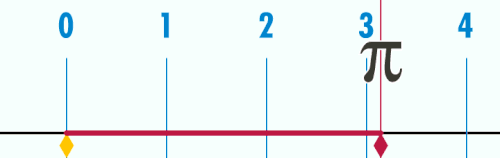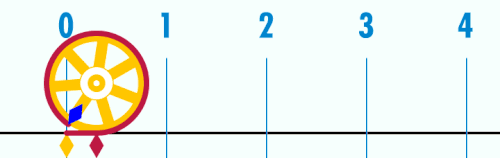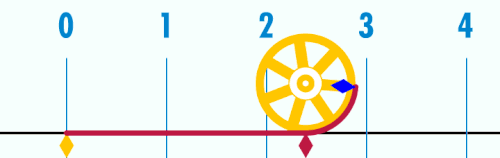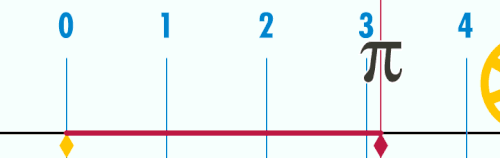
Es gibt natürlich einige geometrische Methoden die Zahl ${}\pi$ zu erhalten, z.B. die Abrollmethode und die Schwimmbadmethode.

Beispiel

Die einfachste Art, die Zahl ${}\pi$ geometrisch zu konstruieren, ist die Abrollmethode, bei der man einen Kreis mit Durchmesser ${}1$ einmal exakt abrollt. Die zurückgeführte Entfernung ist genau der Kreisumfang, also ${}\pi$.

Beispiel

Man kann die Zahl ${}\pi$ auch mit Hilfe von Schwimmbecken und einer idealen Flüssigkeit erhalten.

• 
  Wir starten mit einem Einheitskreis,
• 
  den wir als Grundfläche
• 
  eines Schwimmbeckens der Höhe 1 nehmen.
• 
  Das füllen wir randvoll mit Wasser auf.
• 
  Wir nehmen ein zweites Schwimmbecken mit quadratischer Grundfläche ${}1\times 1$ und Höhe 4.
• 
  Der Inhalt des ersten Schwimmbeckens wird
• 
  in das zweite Schwimmbecken gegossen.
• 
  Der Wasserstand im zweiten Schwimmbecken ist exakt ${}\pi$.

<< | Kurs:Körper- und Galoistheorie (Osnabrück 2018-2019) | >> PDF-Version dieser Vorlesung Arbeitsblatt zur Vorlesung (PDF)