Kurs:Mathematik für Anwender (Osnabrück 2011-2012)/Teil II/Arbeitsblatt 34

Aufwärmaufgaben

Aufgabe

Bestimme die Ableitung der Kurve

$f\colon \mathbb {R} \longrightarrow \mathbb {R} ^{3},\,t\longmapsto f(t)={\left(t^{2}-\sin t,e^{-t}+2t^{3},t\cdot \sinh t+{\frac {1}{t^{2}+1}}\right)},$

in jedem Punkt ${}t\in \mathbb {R}$.

Aufgabe

Skizziere die Bilder und die Graphen der folgenden Kurven im ${}\mathbb {R} ^{2}$.

1. ${}t\longmapsto {\left(t^{2},t^{2}\right)}$,
2. ${}t\longmapsto {\left(t^{2},-t^{2}\right)}$,
3. ${}t\longmapsto {\left(t^{2},t\right)}$,
4. ${}t\longmapsto {\left(2t,3t\right)}$,
5. ${}t\longmapsto {\left(t^{2},t^{3}\right)}$.

Aufgabe

Sei ${}V$ ein euklidischer Vektorraum und ${}v,w\in V$. Zeige, dass die Abbildung

$f\colon \mathbb {R} \longrightarrow V,\,t\longmapsto tv+w,$

differenzierbar ist mit der Ableitung ${}f'(t)=v$.

Aufgabe

Es sei ${}I$ ein reelles Intervall und ${}V$ ein euklidischer Vektorraum. Es seien

$f,g\colon I\longrightarrow V$

zwei in ${}t_{0}\in I$ differenzierbare Kurven und es sei

$h\colon I\longrightarrow \mathbb {R}$

eine in ${}t_{0}$ differenzierbare Funktion. Zeige, dass folgende Aussagen gelten.

1. Die Summe

   $f+g\colon I\longrightarrow V,\,t\longmapsto f(t)+g(t),$

   ist in ${}t_{0}$ differenzierbar mit

   $(f+g)'(t_{0})=f'(t_{0})+g'(t_{0}).$

2. Das Produkt

   $hf\colon I\longrightarrow V,\,t\longmapsto h(t)f(t),$

   ist differenzierbar in ${}t_{0}$ mit

   $(hf)'(t_{0})=h(t_{0})f'(t_{0})+h'(t_{0})f(t_{0}).$

   Insbesondere ist für ${}c\in \mathbb {R}$ auch ${}cf$ differenzierbar in ${}t_{0}$ mit

   $(cf)'(t_{0})=cf'(t_{0}).$

3. Wenn ${}h$ nullstellenfrei ist, so ist auch die Quotientenfunktion

   ${\frac {f}{h}}\colon I\longrightarrow V,\,t\longmapsto {\frac {f(t)}{h(t)}},$

   in ${}t_{0}$ differenzierbar mit

   ${\left({\frac {f}{h}}\right)}'(t_{0})={\frac {h(t_{0})f'(t_{0})-h'(t_{0})f(t_{0})}{(h(t_{0}))^{2}}}.$

Aufgabe

Sei ${}(M,d)$ ein metrischer Raum, sei ${}T\subseteq M$ eine Teilmenge und sei ${}a\in M$ ein Berührpunkt von ${}T$. Es sei

$f\colon T\longrightarrow V$

eine Abbildung in einen euklidischen Vektorraum ${}V$ mit den Komponentenfunktionen

$f_{1},\ldots ,f_{n}\colon T\longrightarrow \mathbb {R}$

bezüglich einer Basis von ${}V$. Zeige, dass der Limes

$\operatorname {lim} _{x\rightarrow a}\,f(x)$

genau dann existiert, wenn sämtliche Limiten

$\operatorname {lim} _{x\rightarrow a}\,f_{j}(x)$

existieren.

Aufgabe

Es seien

$f,g\colon \mathbb {R} \longrightarrow \mathbb {R} ^{n}$

zwei differenzierbare Kurven. Berechne die Ableitung der Funktion

$\mathbb {R} \longrightarrow \mathbb {R} ,\,t\longmapsto \left\langle f(t),g(t)\right\rangle .$

Aufgabe

Für welche Punkte ${}t\in \mathbb {R}$ ist der Abstand der Bildpunkte der Kurve

$\mathbb {R} \longrightarrow \mathbb {R} ^{2},\,t\longmapsto (2\sin t,3\cos t),$

zum Nullpunkt ${}(0,0)$ maximal, für welche minimal?

Aufgabe

Das Bild der durch

$\mathbb {R} \longrightarrow \mathbb {R} ^{2},\,t\longmapsto \left(t^{2},\,t^{3}\right),$

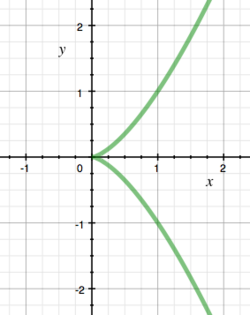
definierten Kurve heißt Neilsche Parabel. Zeige, dass ein Punkt ${}(x,y)\in \mathbb {R} ^{2}$ genau dann zu diesem Bild gehört, wenn er die Gleichung ${}x^{3}=y^{2}$ erfüllt.

Aufgabe (4 Punkte)

Es seien ${}P_{1},\ldots ,P_{n}\in \mathbb {R} ^{2}$ endlich viele Punkte und sei ${}M=\mathbb {R} ^{2}\setminus \{P_{1},\ldots ,P_{n}\}$. Zeige, dass es zu je zwei Punkten ${}P,Q\in M$ eine differenzierbare Kurve

$\varphi \colon [0,1]\longrightarrow M$

mit ${}\varphi (0)=P$ und ${}\varphi (1)=Q$ gibt.

Aufgaben zum Abgeben

Aufgabe (3 Punkte)

Bestimme die Ableitung der Kurve

$\varphi \colon \mathbb {R} _{+}\longrightarrow \mathbb {R} ^{3},\,t\longmapsto {\left({\frac {\sin t^{2}}{t^{5}}},4^{t},{\frac {e^{-t}}{\sqrt {t}}}\right)},$

für jeden Punkt ${}t\in \mathbb {R} _{+}$.

Aufgabe (4 Punkte)

Betrachte die Kurve

$f\colon \mathbb {R} \longrightarrow \mathbb {R} ^{3},\,x\longmapsto \left(x^{2}-x,\,x^{3}+\sinh x,\,\sin(x^{2})\right).$

a) Bestimme die Ableitung von ${}f$ in jedem Punkt ${}x$.

b) Bestimme die Komponentenfunktionen von ${}f$ bezüglich der neuen Basis

$(1,0,3),(2,4,6),(1,-1,0)$

von ${}\mathbb {R} ^{3}$.

c) Berechne die Ableitung in der neuen Basis direkt und mit Hilfe von Lemma 34.10.

Aufgabe (4 (2+1+1) Punkte)

Auf einem Jahrmarkt befindet sich ein „Doppel-Karussell“, bei dem sich ein Sitz alle ${}2$ Sekunden um einen kleinen Kreis mit Radius ${}3$ Meter dreht, wobei sich der Mittelpunkt dieses Kreises seinerseits alle ${}8$ Sekunden um einen großen Kreis mit Radius ${}10$ Meter dreht. Beide Drehungen sind im Uhrzeigersinn. Zum Zeitpunkt ${}t=0$ besitzt der Sitz zum Mittelpunkt den Abstand ${}13$ Meter.

a) Beschreibe diesen Bewegungsvorgang (in einem geeigneten Koordinatensystem) als eine differenzierbare Kurve.

b) Berechne den Geschwindigkeitsvektor dieser Bewegung zu jedem Zeitpunkt.

c) Berechne die Geschwindigkeit (den Betrag des Geschwindigkeitsvektors) dieser Bewegung zu jedem Zeitpunkt.

Aufgabe (6 Punkte)

Bestimme in der Situation von Aufgabe 34.12 die Zeitpunkte, an denen die Geschwindigkeit maximal oder minimal wird.

Aufgabe (4 Punkte)

Sei

$f\colon \mathbb {R} \longrightarrow \mathbb {R} ^{2},\,t\longmapsto \left(t^{2},\,t^{3}\right).$

Bestimme die Punkte ${}t_{0}\in \mathbb {R}$, für die der Abstand der zugehörigen Kurvenpunkte ${}f(t)=\left(t^{2},\,t^{3}\right)$ zum Punkt ${}(1,0)$ minimal wird.

Aufgabe (4 Punkte)

Es sei

$f\colon \mathbb {R} \longrightarrow \mathbb {R} ^{n}$

eine differenzierbare Kurve und ${}P\in \mathbb {R} ^{n}$ ein Punkt. Es sei ${}t_{0}\in \mathbb {R}$ derart, dass der Abstand ${}d(P,f(t))$ (zwischen ${}P$ und einem Kurvenpunkt) in ${}t_{0}$ minimal werde. Zeige, dass ${}P-f(t_{0})$ senkrecht zu ${}f'(t_{0})$ ist.

Aufgabe zum Hochladen

Aufgabe * (6 Punkte)

Erstelle eine Animation zu Aufgabe 34.12.

Fußnoten