Kurs:Mathematik für Anwender (Osnabrück 2011-2012)/Teil II/Vorlesung 38
- Differentialgleichungen höherer Ordnung
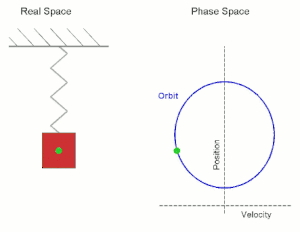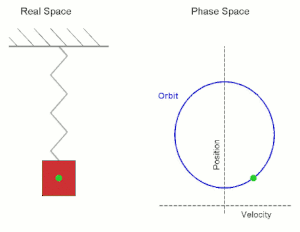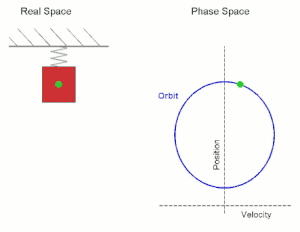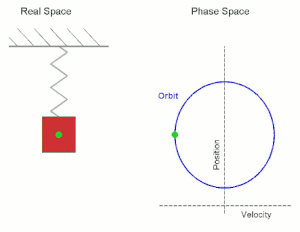
Viele physikalische Bewegungsprozesse sind nicht dadurch determiniert, dass zu jedem Zeit- und Ortspunkt die Bewegungsrichtung (also die gerichtete Geschwindigkeit) vorgegeben wird, sondern dadurch, dass zu jedem Zeit- und Ortspunkt eine Kraft auf ein Teilchen wirkt, die dieses beschleunigt. In diesem Fall kann die Bewegung also nicht durch die erste Ableitung (Geschwindigkeit) modelliert werden, sondern durch die zweite Ableitung (Beschleunigung). Typische Beispiele hierzu sind die durch die Gravitation oder eine Federkraft hervorgerufenen Bewegungen.
Wir betrachten die Bewegung eines Punktes auf einer Geraden, wobei die auf den Punkt (in Richtung des Nullpunkts) wirkende Kraft (bzw. Beschleunigung) proportional zur Lage des Punktes sein soll. Wenn der Punkt sich in befindet und sich in die positive Richtung bewegt, so wirkt diese Kraft bremsend, wenn er sich in die negative Richtung bewegt, so wirkt die Kraft beschleunigend. Mit der Proportionalitätskonstante gelangt man zur Differentialgleichung (zweiter Ordnung)
die diesen Bewegungsvorgang beschreibt. Als Anfangsbedingung wählen wir und , zum Zeitpunkt soll die Bewegung also durch den Nullpunkt gehen und dort die Geschwindigkeit besitzen. Man kann sofort die Lösung
angeben.
Ein Gegenstand der Masse wird aus der Höhe losgelassen und fällt unter dem Einfluss der Gravitation zu Boden. Dabei wirkt auf den Körper einerseits die Gravitationskraft (die Erdbeschleunigung nehmen wir für diesen Bewegungsvorgang als konstant an), die ihn beschleunigt, andererseits wird diese Beschleunigung durch den Luftwiderstand verringert. Nach einem physikalischen Gesetz ist die Reibung (bei relativ kleinen Geschwindigkeiten) proportional und entgegengesetzt zur Geschwindigkeit des Körpers. Es sei der Reibungswiderstand, also dieser Proportionalitätsfaktor. Die auf den Körper (nach unten) wirkende Gesamtkraft ist daher
Wegen
gilt daher für diesen Bewegungsvorgang die Differentialgleichung zweiter Ordnung
Wenn wir dies mit der Ableitungsfunktion schreiben, so erhalten wir die Bedingung
die nach Beispiel 29.11 die Lösungen
besitzt. Durch Intergration erhält man für die Differentialgleichung zweiter Ordnung die Lösungsfunktionen
Es sei ein offenes Intervall, offen und
eine Funktion. Dann nennt man den Ausdruck
eine Differentialgleichung der Ordnung .
Unter einer Lösung einer Differentialgleichung höherer Ordnung versteht man eine -mal differenzierbare Funktion
(wobei ein offenes Teilintervall ist) derart, dass
für alle gilt.
Differentialgleichungen beliebiger Ordnung können unter Inkaufnahme von neuen Variablen auf ein Differentialgleichungssystem erster Ordnung zurückgeführt werden.
Es sei ein Intervall, eine offene Menge und
eine Funktion.
Dann ist die Differentialgleichung höherer Ordnung
über die Beziehung
äquivalent zum Differentialgleichungssystem
Wenn
eine Lösung der Differentialgleichung höherer Ordnung
ist, so sind alle Funktionen für differenzierbar, und es gilt für nach Definition und schließlich
Wenn umgekehrt
eine Lösung des Differentialgleichungssystems zum Vektorfeld
ist, so ergibt sich sukzessive aus den ersten Gleichungen, dass -mal differenzierbar ist, und die letzte Gleichung des Differentialgleichungssystems besagt gerade
Mit dieser Umformung ist auch klar, wie sinnvolle Anfangsbedingungen für eine Differentialgleichung höherer Ordnung aussehen. Man muss nicht nur einen Startwert
,
sondern auch die höheren Ableitungen
,
,
usw. festlegen.
Es ist im Allgemeinen schwierig, eine Differentialgleichung explizit zu lösen. Wir besprechen daher zunächst zwei approximierende Verfahren, nämlich das eulersche Polygonzugverfahren und den Potenzreihenansatz.
- Polygonzugverfahren
Mit dem (eulerschen) Polygonzugverfahren wird die Lösungskurve einer Differentialgleichung diskret approximiert.
Es sei ein Vektorfeld
auf einer offenen Menge und eine Anfangsbedingung gegeben. Das eulersche Polygonzugverfahren funktioniert folgendermaßen: Man wählt eine Schrittweite und berechnet rekursiv die Punktfolge , , durch und
Zu einem schon konstruierten Punkt wird also das -fache des Richtungsvektors zum Zeitpunkt an diesem Punkt hinzuaddiert. Dies funktioniert nur, solange die Punkte im Definitionsbereich des Vektorfeldes liegen. Der zu dieser Punktfolge gehörende Streckenzug oder Polygonzug
ist die lineare Interpolation mit , d.h. für mit ist
Dieser Streckenzug stellt eine stückweise lineare Approximation der Lösungskurve des Anfangswertproblems dar. Für eine kleinere Schrittweite wird die Approximation im Allgemeinen besser.
Bei einer eindimensionalen ortsunabhängigen Differentialgleichung
ergibt sich einfach als eine Stammfunktion zu . Wendet man in dieser Situation Verfahren 38.5 zum Startzeitpunkt , zum Startpunkt und zur Schrittweite an, so ergibt sich die rekursive Beziehung
Daher ist offenbar
D.h. dass man zu dem Ausgangswert das Treppenintegral zur äquidistanten Unterteilung (und zur durch auf dem Teilintervall gegebenen Treppenfunktion) hinzuaddiert. Der zugehörige Streckenzug ist die (stückweise lineare) Integralfunktion zu dieser Treppenfunktion.
Wir wollen für das Differentialgleichungssystem
mit der Anfangsbedingung
gemäß Verfahren 38.5 einen approximierenden Streckenzug berechnen. Wir wählen die Schrittweite . Somit ist
und
- Potenzreihenansatz
Nicht alle Differentialgleichungen sind explizit lösbar, und selbst wenn es eine explizite Lösung gibt, so ist es häufig schwierig, diese zu finden. Statt der vollen Information einer Lösungskurve begnügt man sich häufig mit der Teilinformation, die in der Taylor-Entwicklung der Kurve (bis zu einem bestimmten Grad) enthalten ist, d.h. man bestimmt gewisse Ableitungen der Kurve zu einem bestimmten Zeit- und Ortspunkt. Diese Information kann man häufig direkt aus der Differentialgleichung ablesen, ohne die Lösungskurve zu bestimmen. Diese Vorgehensweise setzt voraus, dass das Vektorfeld durch „analytische“ (beispielsweise polynomiale) Daten gegeben ist.
Es sei ein Anfangswertproblem
zu einem Vektorfeld
gegeben, wobei die Komponentenfunktionen , , polynomial (oder durch Potenzreihen gegeben) seien. Dann lässt sich ein Potenzreihenansatz für die Lösung durchführen. Das bedeutet, dass man den Ansatz mit unbestimmten Koeffizienten macht, und diese Koeffizienten (bis zu einem gewünschten Grad) aus den Gleichungen
sukzessive bestimmt. Die Anfangsbedingungen
legen dabei die konstanten Koeffizienten der Potenzreihen fest. In das Differentialgleichungssystem werden die Potenzreihen links und rechts eingesetzt und ausgewertet, wobei die Ableitung links formal zu nehmen ist und rechts die Reihen formal zu addieren und zu multiplizieren sind. Dies ergibt Gleichungen für Potenzreihen in , die durch Koeffizientenvergleich, beginnend mit den Koeffizienten von kleinem Grad, gelöst werden können.
Wir betrachen das Anfangswertproblem
und wollen es mit einem Potenzreihenansatz lösen. Es sei also
die auszuwertende Potenzreihengleichung ist somit
Die Anfangsbedingung legt fest. Für den konstanten Term (also zu ) ergibt sich aus der Potenzreihengleichung
Für ergibt sich
Für ergibt sich
also ist . Für ergibt sich
also ist . Für ergibt sich
also ist . Die Taylor-Entwicklung der Lösungskurve bis zur Ordnung ist demnach
Wir betrachten das Anfangswertproblem
und machen den Potenzreihenansatz und . Aufgrund der Anfangsbedingung ist
Das Differentialgleichungssystem führt auf die beiden Potenreihengleichungen
und
die wir gradweise auswerten. Für den Grad (der Potenzreihengleichungen) ergeben sich daraus die beiden Gleichungen
Für den Grad ergeben sich daraus die beiden Gleichungen
also ist und . Für den Grad ergeben sich daraus die beiden Gleichungen
also ist und . Für den Grad ergeben sich daraus die beiden Gleichungen
also ist und . Die Taylor-Entwicklung der Lösungskurve bis zur Ordnung ist demnach
Eine Differentialgleichung höherer Ordnung
kann man entsprechend Verfahren 38.8 mit einem Potenzreihenansatz, also mit einem Ansatz der Form
mit unbestimmten Koeffizienten , (bis zu einer gewissen Ordnung) lösen. Dazu muss die Funktion polynomial (oder durch eine Potenzreihe gegeben) sein. Damit die Lösung eindeutig ist, müssen zusätzlich Anfangsbedingungen
vorgegeben sein. Die Koeffizienten werden sukzessive unter Verwendung der Differentialgleichung und der Anfangsbedingungen gelöst.
Wir betrachen das Anfangswertproblem
und wollen es mit einem Potenzreihenansatz lösen. Es sei also
die auszuwertende Potenzreihengleichung ist somit
Die Anfangsbedingung legt und fest. Für den konstanten Term (also zu ) ergibt sich aus der Potenzreihengleichung
also ist . Für ergibt sich
also ist . Für ergibt sich
also ist . Für ergibt sich
also ist . Die Taylor-Entwicklung der Lösungskurve bis zur Ordnung ist demnach
| << | Kurs:Mathematik für Anwender (Osnabrück 2011-2012)/Teil II | >> |
|---|