Kurs:Mathematik (Osnabrück 2009-2011)/Teil II/Vorlesung 54
- Zur Eindeutigkeit der Lösungen von Differentialgleichungen
Es sei ein endlichdimensionaler reeller Vektorraum, ein reelles Intervall, eine offene Menge und
ein stetiges Vektorfeld auf das lokal einer Lipschitz-Bedingung genügt. Es sei ein offenes Teilintervall und es seien
Lösungen des Anfangswertproblems
Dann ist .
Wir betrachten die Menge
Wegen
ist diese Menge nicht leer.
Zu jedem Punkt
gibt es nach
Satz 53.4
eine offene Intervallumgebung
,
worauf es zu gegebener Anfangsbedingung
genau eine Lösung der Differentialgleichung gibt. Wenn
ist, so ist
und daher stimmen
und
in einer offenen Umgebung
mit der eindeutigen Lösung und damit untereinander überein. Also ist
.
Dies bedeutet, dass eine
offene
Teilmenge von ist.
Andererseits sind
und
stetig
und daher ist nach
Aufgabe 54.1
die Menge auch
abgeschlossen
in .
Da ein Intervall
nach Satz 21.2 zusammenhängend
ist, folgt
.
Das folgende Beispiel zeigt, dass ohne die Lipschitz-Bedingung die Lösung eines Anfangswertproblems nicht eindeutig bestimmt ist.
Wir betrachten das Anfangswertproblem
zum zeitunabhängigen Vektorfeld
Offensichtlich gibt es die stationäre Lösung
aber auch
ist eine Lösung, wie man durch Nachrechnen sofort bestätigt. Aus diesen beiden Lösungen kann man sich noch weitere Lösungen basteln. Es seien dazu reelle Zahlen. Dann ist auch
eine Lösung. D.h. es gibt Lösungen, bei denen das Teilchen beliebig lange (im Zeitintervall von nach ) ruht und danach (und davor) sich bewegt. Sobald sich das Teilchen in einem Punkt befindet, ist der Bewegungsablauf lokal eindeutig bestimmt.
Zu einem stetigen Vektorfeld
kann man sich fragen, ob es ein maximales Definitionsintervall für die Lösung eines Anfangswertproblems
gibt. Dies ist in der Tat der Fall, wenn das Vektorfeld lokal einer Lipschitz-Bedingung genügt! Man kann nämlich alle Teilmengen
betrachten. Wegen Satz 54.1 stimmen zwei Lösungen und auf dem Durchschnitt überein, und liefern daher eine eindeutige Lösung auf der Vereinigung . Daher enthält die Menge der Teilintervalle, auf denen eine Lösung definiert ist, ein maximales Teilintervall .
Dieses Teilintervall kann kleiner als sein. Die Grenzen des maximalen Teilintervalls, auf dem eine Lösung definiert ist, heißen auch Entweichzeiten.
- Gradientenfelder
Es sei ein euklidischer Vektorraum, offen und
eine differenzierbare Funktion. Dann nennt man die Abbildung
das zugehörige Gradientenfeld.
Ein Gradientenfeld ist also ein zeitunabhängiges Vektorfeld. Man spricht auch von einem Potentialfeld, die Funktion (manchmal ) heißt dann ein Potential des Vektorfeldes. Wenn zweimal stetig differenzierbar ist, so genügt nach Lemma 52.10 das zugehörige Gradientenfeld lokal einer Lipschitz-Bedingung.
Die folgende Aussage zeigt, dass die Lösungskurven der zugehörigen Differentialgleichung senkrecht auf den Fasern von liegen. Die Fasern beschreiben, wo das Potential (oder die Höhenfunktion) konstant ist, die Lösungen beschreiben nach Satz 46.3 den Weg des steilsten Anstiegs. Wenn beispielsweise die Höhenfunktion eines Gebirges ist, so gibt das Gradientenfeld in jedem Punkt den steilsten Anstieg an und die Trajektorie einer Lösungskurve beschreibt den Verlauf eines Baches (wir behaupten nicht, dass die Bewegung eines Wassermoleküls im Bach durch diese Differentialgleichung bestimmt ist, sondern lediglich, dass der zurückgelegte Weg, also das Bild der Kurve, mit dem Bild der Lösungskurve übereinstimmt). Der Bach verläuft immer senkrecht zu den Höhenlinien.
Es sei ein euklidischer Vektorraum, offen,
eine differenzierbare Funktion und
das zugehörige Gradientenfeld. Es sei
eine Lösung der Differentialgleichung
Dann steht senkrecht auf dem Tangentialraum der Faser von durch für , für die reguläre Punkte von sind.
Sei ein regulärer Punkt von und sei ein Vektor aus dem Tangentialraum. Dann gilt direkt
Wir betrachten die Produktabbildung
Das zugehörige Gradientenfeld ist
Die Fasern von sind das Achsenkreuz (die Faser über ) und die durch , , gegebenen Hyperbeln. Die Lösungen der linearen Differentialgleichung
sind von der Form
mit beliebigen , wie man direkt nachrechnet und was sich auch aus Lemma 56.1 bzw. Aufgabe ***** ergibt. Dabei ist . Für ist dies die stationäre Lösung im Nullpunkt, in dem die Produktabbildung nicht regulär ist. Bei ist , das Bild dieser Lösung ist die obere Halbdiagonale (ohne den Nullpunkt), bei ist , das Bild dieser Lösung ist die untere Halbdiagonale, bei und ist , das Bild dieser Lösung ist die untere Hälfte der Nebendiagonalen, bei und ist , das Bild dieser Lösung ist die obere Hälfte der Nebendiagonalen.
Ansonsten treffen die Lösungskurven das Achsenkreuz in einem Punkt . Wenn man diesen Punkt als Anfangswert zum Zeitpunkt nimmt, so kann man die Lösungskurven als
(zum Zeitpunkt befindet sich die Lösung auf der Achse im Punkt ),
und als(zum Zeitpunkt befindet sich die Lösung auf der Achse im Punkt ) realisieren. Die Bahnen dieser Lösungen erfüllen die Gleichung bzw. , d.h. sie sind selbst Hyperbeln.
- Differentialgleichungen höherer Ordnung
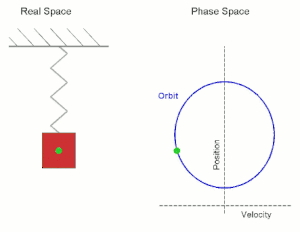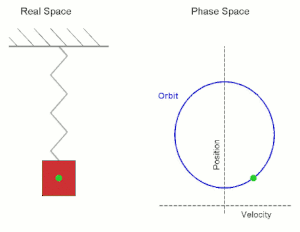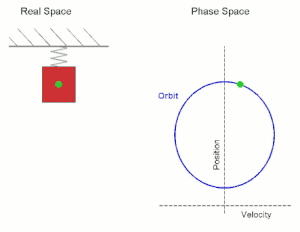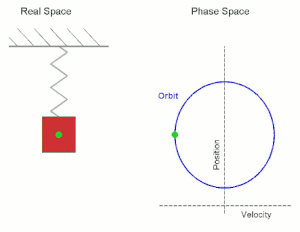
Viele physikalische Bewegungsprozesse sind nicht (wie im Fall eines Löwenzahnfallschirmchens, siehe Vorlesung 37) dadurch determiniert, dass zu jedem Zeit- und Ortspunkt die Bewegungsrichtung (also die gerichtete Geschwindigkeit) vorgegeben wird, sondern dadurch, dass zu jedem Zeit- und Ortspunkt eine Kraft auf ein Teilchen wirkt, die dieses beschleunigt. In diesem Fall kann die Bewegung also nicht durch die erste Ableitung (Geschwindigkeit) modelliert werden, sondern durch die zweite Ableitung (Beschleunigung). Typische Beispiele hierzu sind die durch Gravitation oder Federkraft hervorgerufenen Bewegungen.
Es sei ein offenes Intervall, offen und
eine Funktion. Dann nennt man den Ausdruck
eine Differentialgleichung der Ordnung .
Unter einer Lösung einer Differentialgleichung höherer Ordnung versteht man eine -mal differenzierbare Funktion
(wobei ein offenes Teilintervall ist) derart, dass
für alle gilt.
Differentialgleichungen beliebiger Ordnung können unter Inkaufnahme von neuen Variablen auf ein Differentialgleichungssystem erster Ordnung zurückgeführt werden.
Es sei ein Intervall, eine offene Menge und
eine Funktion.
Dann ist die Differentialgleichung höherer Ordnung
über die Beziehung
äquivalent zum Differentialgleichungssystem
Wenn
eine Lösung der Differentialgleichung höherer Ordnung
ist, so sind alle Funktionen für differenzierbar, und es gilt für nach Definition und schließlich
Wenn umgekehrt
eine Lösung des Differentialgleichungssystems zum Vektorfeld
ist, so ergibt sich sukzessive aus den ersten Gleichungen, dass -mal differenzierbar ist, und die letzte Gleichung des Differentialgleichungssystems besagt gerade
Mit dieser Umformung ist auch klar, wie sinnvolle Anfangsbedingungen für eine Differentialgleichung höherer Ordnung aussehen. Man muss nicht nur einen Startwert
,
sondern auch die höheren Ableitungen
,
,
usw. festlegen.
| << | Kurs:Mathematik (Osnabrück 2009-2011)/Teil II | >> |
|---|

























![{\displaystyle f\colon \mathbb {R} \longrightarrow \mathbb {R} ,\,v\longmapsto 3v^{2/3}=3{\sqrt[{3}]{v^{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b10707eb391264abba326c5d368f7f17b1a844a7)