Kurs:Mathematik für Anwender (Osnabrück 2019-2020)/Teil I/Repetitorium/Vorlesung 16
- Ableitung von Potenzreihen
Viele wichtige Funktionen wie die Exponentialfunktion oder die trigonometrischen Funktionen werden durch eine Potenzreihe dargestellt. Der folgende Satz zeigt, dass diese Funktionen differenzierbar sind und ihre Ableitung durch diejenige Potenzreihe dargestellt wird, die sich durch gliedweises Ableiten ergibt.
Es sei
eine Potenzreihe, die auf dem offenen Intervall konvergiere und dort die Funktion darstellt.
Dann ist auch die formal abgeleitete Potenzreihe
auf konvergent. Die Funktion ist in jedem Punkt dieses Intervalls differenzierbar mit
Der Beweis erfordert ein genaues Studium von Potenzreihen.
Im Satz haben wir für die Potenzreihe und für die dadurch festgelegte Funktion geschrieben, um die Rollen deutlicher zu machen. Von nun an ist diese Unterscheidung nicht mehr nötig.
Eine durch eine Potenzreihe gegebene Funktion
ist auf ihrem Konvergenzintervall unendlich oft differenzierbar.
Dies ergibt sich direkt aus Satz 16.1.
Nach Definition 12.15 ist
Die Ableitung nach ist aufgrund von Satz 16.3 unter Verwendung der Kettenregel gleich
Bei einer reellen Exponentialfunktion
gilt nach Satz 16.4 die Beziehung
es besteht also ein proportionaler Zusammenhang zwischen der Funktion und ihrer Ableitung mit dem Proportionalitätsfaktor . Dies gilt auch dann, wenn mit einer Konstanten multipliziert wird. Wenn man unter eine von der Zeit abhängige Größe versteht, so beschreibt das momentane Wachstum zu einem Zeitpunkt. Die Gleichung bedeutet dann, dass das momentane Wachstum in jedem Zeitpunkt proportional zur momentanen Größe ist. Ein solches Wachstum (bzw. Schrumpfung bei bzw. ) kommt in der Natur bei einer Population dann vor, wenn es keine nennenswerte Nahrungskonkurrenz und vernachlässigbare Sterberaten gibt (die Anzahl der Mäuse ist dann proportional zur Anzahl der geborenen Mäuse). Eine Bedingung der Form
ist ein Beispiel für eine Differentialgleichung. Dies ist eine Gleichung für eine Funktion, die Bedingungen an die Ableitung der Funktion ausdrückt. Eine Lösung einer solchen Differentialgleichung ist eine differenzierbare Funktion, die diese Ableitungsbedingung erfüllt. Die Lösungen der zuletzt formulierten Differentialgleichung sind die Funktionen
Wir werden uns im zweiten Semester mit Differentialgleichungen intensiv beschäftigen.
Nach Definition 12.15 ist
Die Ableitung nach ist aufgrund von Satz 16.3 und Korollar 16.6 unter Verwendung der Kettenregel gleich
Aufgrund der Quotientenregel, Satz 16.8 und der Kreisgleichung ergibt sich
Das Argument für die Ableitung des Kotangens ist entsprechend.
- Die Zahl
Die Zahl ist der Flächeninhalt bzw. der halbe Kreisumfang eines Kreises mit Radius . Um darauf eine präzise Definition dieser Zahl aufzubauen müsste man zuerst die Maßtheorie (bzw. die Länge von „krummen Kurven“) entwickeln. Auch die trigonometrischen Funktionen haben eine intuitive Interpretation am Einheitskreis, doch auch diese setzt das Konzept der Bogenlänge voraus. Ein alternativer Zugang ist es, die Zahl über analytische Eigenschaften der durch ihre Potenzreihen definierten Funktionen Sinus und Kosinus zu definieren und dann erst nach und nach die Beziehung zum Kreis herzustellen (siehe Beispiel 20.10 und Beispiel *****).
Die Kosinusfunktion
besitzt im reellen Intervall genau eine Nullstelle.
Wir betrachten die Kosinusreihe
Für ist . Für kann man geschickt klammern und erhält
Nach dem
Zwischenwertsatz
gibt es also mindestens eine Nullstelle im angegebenen Intervall.
Zum Beweis der Eindeutigkeit betrachten wir die
Ableitung
des Kosinus, diese ist nach
Satz 16.8
Es genügt zu zeigen, dass der Sinus im Intervall positiv ist, denn dann ist das Negative davon stets negativ und der Kosinus ist dann nach Satz 15.7 im angegebenen Intervall streng fallend, sodass es nur eine Nullstelle gibt. Für gilt
Es sei die eindeutig bestimmte reelle Nullstelle der Kosinusfunktion aus dem Intervall . Die Kreiszahl ist durch
definiert.
Die Sinusfunktion und die Kosinusfunktion erfüllen in folgende Periodizitätseigenschaften.
- Es ist und für alle .
- Es ist und für alle .
- Es ist und für alle .
- Es ist , , , und .
- Es ist , , , und .
Aufgrund der Kreisgleichung
ist , also ist wegen der Überlegung im Beweis zu Lemma 16.10. Daraus folgen mit den Additionstheoremen die in (3) angegebenen Beziehungen zwischen Sinus und Kosinus, beispielsweise ist
Es genügt daher, die Aussagen für den Kosinus zu beweisen. Alle Aussagen folgen dann aus der Definition von und aus (3).
Die beiden trigonometrischen Funktionen sind also periodische Funktionen mit der Periodenlänge .
- Die inversen trigonometrischen Funktionen
induziert eine bijektive, streng wachsende Funktion
und die reelle Kosinusfunktion induziert eine bijektive streng fallende Funktion
Beweis
Die reelle Tangensfunktion induziert eine bijektive, streng wachsende Funktion
und die reelle Kotangensfunktion induziert eine bijektive streng fallende Funktion
Beweis
Aufgrund der Bijektivität von Sinus, Kosinus, Tangens und Kotangens auf geeigneten Intervallen gibt es die folgenden Umkehrfunktionen.
Die inversen trigonometrischen Funktionen besitzen die folgenden Ableitungen.
Für den Arkustangens gilt beispielsweise nach Satz 14.9
| << | Kurs:Mathematik für Anwender (Osnabrück 2019-2020)/Teil I/Repetitorium | >> |
|---|


![{\displaystyle {}]-r,r[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be92ec31de8ca4b998ea7227b7b3b5c363713765)
![{\displaystyle {}f\colon ]-r,r[\rightarrow \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9986ed78b089d43e6e6ca0846ffe3ff3e49d02ca)













































![{\displaystyle {}[0,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16a500881b91a2cffe370f70cb70d470f894e184)






![{\displaystyle {}]0,2[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad4b5eda7dcd4e7f1ff19cca0efe58996d75e76e)
![{\displaystyle {}x\in {]0,2]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87a6aae3d6ff3d676031259a6b2448264371119c)





























![{\displaystyle [-\pi /2,\pi /2]\longrightarrow [-1,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/527f8bc31212ec82e3778cde36b1ed32192bf657)
![{\displaystyle [0,\pi ]\longrightarrow [-1,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8dbd9728b307c63938254cd4e4aff49bc8e2f2a7)
![{\displaystyle ]-\pi /2,\pi /2[\longrightarrow \mathbb {R} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f54b80848470e2b293193379bd774648a7d69df6)
![{\displaystyle ]0,\pi [\longrightarrow \mathbb {R} .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ee76be0ff249a9e5158134ec10b2585d1deacb1)

![{\displaystyle [-1,1]\longrightarrow [-{\frac {\pi }{2}},{\frac {\pi }{2}}],\,x\longmapsto \arcsin x,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c24a8a90340b8ae29506b60069c96a906c84497)

![{\displaystyle [-1,1]\longrightarrow [0,\pi ],\,x\longmapsto \arccos x,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/204deb80b68913b620eba6f2a76dd3db16804d7a)
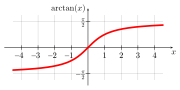
![{\displaystyle \mathbb {R} \longrightarrow ]-{\frac {\pi }{2}},{\frac {\pi }{2}}[,\,x\longmapsto \arctan x,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa0f4921b59ab4688759dda8d4bbf7ccb8deab26)

![{\displaystyle \mathbb {R} \longrightarrow ]0,\pi [,\,x\longmapsto \operatorname {arccot} x,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d619690f844a8f2dba9e0c98f4850e0b255be06a)




