Kurs:Mathematik für Anwender (Osnabrück 2019-2020)/Teil I/Repetitorium/Vorlesung 26

„Man muß nur Ein Wesen recht von Grund aus lieben, da kommen einem die übrigen alle liebenswürdig vor!“

Johann Wolfgang von Goethe

Rang von Matrizen

Definition

Es sei ${}K$ ein Körper und sei ${}M$ eine ${}m\times n$- Matrix über ${}K$. Dann nennt man die Dimension des von den Spalten erzeugten Untervektorraums von ${}K^{m}$ den (Spalten-)Rang der Matrix, geschrieben

$\operatorname {rang} \,M.$

Lemma

Es sei ${}K$ ein Körper und es seien ${}V$ und ${}W$ Vektorräume über ${}K$ der Dimension ${}n$ bzw. ${}m$. Es sei

$\varphi \colon V\longrightarrow W$

eine lineare Abbildung, die bezüglich zweier Basen durch die Matrix ${}M\in \operatorname {Mat} _{m\times n}(K)$ beschrieben werde.

Dann gilt

${}\operatorname {rang} \,\varphi =\operatorname {rang} \,M\,.$

Beweis

Siehe Aufgabe 26.21.

$\Box$

Zur Formulierung der nächsten Aussage führen wir den Zeilenrang einer ${}m\times n$-Matrix als die Dimension des von den Zeilen erzeugten Untervektorraumes von ${}K^{n}$ ein.

Lemma

Es sei ${}K$ ein Körper und sei ${}M$ eine ${}m\times n$- Matrix über ${}K$.

Dann stimmt der Spaltenrang mit dem Zeilenrang überein.

Wenn man ${}M$ im Sinne von Satz 21.9 mittels elementarer Zeilenumformungen in eine Matrix ${}M'$ in Stufenform transformiert, so ist der Rang gleich der Anzahl der relevanten Zeilen von ${}M'$.

Beweis

Es sei ${}r$ die Anzahl der relevanten Zeilen in der durch elementare Zeilenumformungen gewonnenen Matrix ${}M'$ in Stufenform. Wir zeigen, dass diese Zahl sowohl mit dem Spaltenrang als auch mit dem Zeilenrang von ${}M'$ und von ${}M$ übereinstimmt. Bei elementaren Zeilenumformungen ändert sich der von den Zeilen erzeugte Untervektorraum nicht, und damit ändert sich auch nicht der Zeilenrang. Der Zeilenrang von ${}M$ stimmt also mit dem Zeilenrang von ${}M'$ überein. Diese Matrix hat den Zeilenrang ${}r$, da die ersten ${}r$ Zeilen linear unabhängig sind und ansonsten nur Nullzeilen auftauchen. Sie hat aber auch den Spaltenrang ${}r$, da die ${}r$ Spalten, in denen eine neue Stufe auftritt, linear unabhängig sind und die weiteren Spalten Linearkombinationen dieser ${}r$ Spalten sind. Die Aufgabe 26.2 zeigt, dass sich bei elementaren Zeilenumformungen auch der Spaltenrang nicht ändert.

$\Box$

Beide Ränge stimmen also überein, so dass wir im Folgenden nur noch vom Rang einer Matrix sprechen werden.

Korollar

Es sei ${}K$ ein Körper und sei ${}M$ eine ${}n\times n$- Matrix über ${}K$. Dann sind folgende Aussagen äquivalent.

1. ${}M$ ist invertierbar.
2. Der Rang von ${}M$ ist ${}n$.
3. Die Zeilen von ${}M$ sind linear unabhängig.
4. Die Spalten von ${}M$ sind linear unabhängig.

Beweis

Die Äquivalenz von (2), (3) und (4) folgt aus der Definition und aus Lemma 26.3.
Für die Äquivalenz von (1) und (2) betrachten wir die durch ${}M$ definierte lineare Abbildung

$\varphi \colon K^{n}\longrightarrow K^{n}.$

Die Eigenschaft, dass der Spaltenrang gleich ${}n$ ist, ist äquivalent zur Surjektivität der Abbildung, die aufgrund von Korollar 25.4 äquivalent zur Bijektivität der Abbildung ist. Die Bijektivität ist nach Lemma 25.11 äquivalent zur Invertierbarkeit der Matrix.

$\Box$

Determinanten

Definition

Es sei ${}K$ ein Körper und sei ${}M={\left(a_{ij}\right)}_{ij}$ eine ${}n\times n$- Matrix über ${}K$. Zu ${}i\in {\{1,\ldots ,n\}}$ sei ${}M_{i}$ diejenige ${}(n-1)\times (n-1)$-Matrix, die entsteht, wenn man in ${}M$ die erste Spalte und die ${}i$-te Zeile weglässt. Dann definiert man rekursiv die Determinante von ${}M$ durch

${}\det M={\begin{cases}a_{11}\,,&{\text{falls }}n=1\,,\\\sum _{i=1}^{n}(-1)^{i+1}a_{i1}\det M_{i}&{\text{ für }}n\geq 2\,.\end{cases}}\,$

Die Determinante ist nur für quadratische Matrizen definiert. Die in der Definition auftretenden Matrizen nennt auch Streichungsmatrizen. Für kleine ${}n$ kann man die Determinante einfach ausrechnen.

Beispiel

Für eine ${}2\times 2$-Matrix

${}M={\begin{pmatrix}a&b\\c&d\end{pmatrix}}\,$

ist

$\det {\begin{pmatrix}a&b\\c&d\end{pmatrix}}=ad-cb.$

Als Merkregel für eine ${}3\times 3$-Matrix verwendet man die Regel von Sarrus. Man wiederholt die erste Spalte als vierte Spalte und die zweite Spalte als fünfte Spalte. Die Produkte der durchgezogenen Diagonalen werden positiv genommen, die Produkte der gestrichelten Diagonalen negativ.

Beispiel

Für eine ${}3\times 3$- Matrix ${}M={\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{pmatrix}}$ ist

$\det {\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{pmatrix}}=a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{13}a_{22}a_{31}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}.$

Dies nennt man die Regel von Sarrus.

Lemma

Für eine obere Dreiecksmatrix

${}M={\begin{pmatrix}b_{1}&\ast &\cdots &\cdots &\ast \\0&b_{2}&\ast &\cdots &\ast \\\vdots &\ddots &\ddots &\ddots &\vdots \\0&\cdots &0&b_{n-1}&\ast \\0&\cdots &\cdots &0&b_{n}\end{pmatrix}}\,$

ist

${}\det M=b_{1}b_{2}{\cdots }b_{n-1}b_{n}\,.$

Insbesondere ist für die Einheitsmatrix ${}\det E_{n}=1$.

Beweis

Dies folgt mit einer einfachen Induktion direkt aus der Definition der Determinante.

$\Box$

Multilinearität

Wir wollen zeigen, dass die oben rekursiv definierte Determinante eine „multilineare“ „alternierende“ Abbildung ist, wenn man die Identifizierung

${}\operatorname {Mat} _{n}(K)\cong (K^{n})^{n}\,$

vornimmt, bei der einer Matrix das ${}n$-Tupel der Zeilen der Matrix zugeordnet wird. Wir fassen also im Folgenden eine Matrix als ein Spaltentupel

${\begin{pmatrix}v_{1}\\\vdots \\v_{n}\end{pmatrix}}$

auf, wobei die einzelnen Einträge ${}v_{i}$ Zeilenvektoren der Länge ${}n$ sind.

Satz

Es sei ${}K$ ein Körper und ${}n\in \mathbb {N} _{+}$.

Dann ist die Determinante

$\operatorname {Mat} _{n}(K)=(K^{n})^{n}\longrightarrow K,\,M\longmapsto \det M,$

multilinear.

D.h., dass für jedes ${}k\in {\{1,\ldots ,n\}}$, für je ${}n-1$ Vektoren ${}v_{1},\ldots ,v_{k-1},v_{k+1},\ldots ,v_{n}\in K^{n}$ und für ${}u,w\in K^{n}$ die Gleichheit

${}\det {\begin{pmatrix}v_{1}\\\vdots \\v_{k-1}\\u+w\\v_{k+1}\\\vdots \\v_{n}\end{pmatrix}}=\det {\begin{pmatrix}v_{1}\\\vdots \\v_{k-1}\\u\\v_{k+1}\\\vdots \\v_{n}\end{pmatrix}}+\det {\begin{pmatrix}v_{1}\\\vdots \\v_{k-1}\\w\\v_{k+1}\\\vdots \\v_{n}\end{pmatrix}}\,$

und für ${}s\in K$ die Gleichheit

${}\det {\begin{pmatrix}v_{1}\\\vdots \\v_{k-1}\\su\\v_{k+1}\\\vdots \\v_{n}\end{pmatrix}}=s\det {\begin{pmatrix}v_{1}\\\vdots \\v_{k-1}\\u\\v_{k+1}\\\vdots \\v_{n}\end{pmatrix}}\,$

gilt.

Beweis

Dieser Beweis wurde in der Vorlesung nicht vorgeführt.

Es seien

$M:={\begin{pmatrix}v_{1}\\\vdots \\v_{k-1}\\u\\v_{k+1}\\\vdots \\v_{n}\end{pmatrix}}\,,M':={\begin{pmatrix}v_{1}\\\vdots \\v_{k-1}\\w\\v_{k+1}\\\vdots \\v_{n}\end{pmatrix}}{\text{ und }}{\tilde {M}}:={\begin{pmatrix}v_{1}\\\vdots \\v_{k-1}\\u+w\\v_{k+1}\\\vdots \\v_{n}\end{pmatrix}},$

wobei wir die Einträge und die Streichungsmatrizen analog bezeichnen. Insbesondere ist also ${}u=\left(a_{k1},\,\ldots ,\,a_{kn}\right)$ und ${}w=\left(a_{k1}',\,\ldots ,\,a_{kn}'\right)$. Wir beweisen die Aussage des Satzes durch Induktion nach ${}n$, wobei der Fall ${}n=1$ klar ist. Für ${}i\neq k$ ist ${}{\tilde {a}}_{i1}=a_{i1}=a'_{i1}$ und

${}\det {\tilde {M}}_{i}=\det M_{i}+\det M'_{i}\,$

nach Induktionsvoraussetzung. Für ${}i=k$ ist ${}M_{k}=M_{k}'={\tilde {M}}_{k}$ und es ist ${}{\tilde {a}}_{k1}=a_{k1}+a'_{k1}$. Insgesamt ergibt sich

${}{\begin{aligned}\det {\tilde {M}}&=\sum _{i=1}^{n}(-1)^{i+1}{\tilde {a}}_{i1}\det {\tilde {M}}_{i}\\&=\sum _{i=1,\,i\neq k}^{n}(-1)^{i+1}a_{i1}(\det {M}_{i}+\det {M}'_{i})+(-1)^{k+1}(a_{k1}+a'_{k1})(\det {\tilde {M}}_{k})\\&=\sum _{i=1,\,i\neq k}^{n}(-1)^{i+1}a_{i1}\det {M}_{i}+\sum _{i=1,\,i\neq k}^{n}(-1)^{i+1}a_{i1}\det {M}'_{i}+(-1)^{k+1}a_{k1}\det M_{k}+(-1)^{k+1}a'_{k1}\det M_{k}\\&=\sum _{i=1}^{n}(-1)^{i+1}a_{i1}\det {M}_{i}+\sum _{i=1,\,i\neq k,\,}^{n}(-1)^{i+1}a_{i1}\det {M}'_{i}+(-1)^{k+1}a'_{k1}\det M_{k}\\&=\sum _{i=1}^{n}(-1)^{i+1}a_{i1}\det {M}_{i}+\sum _{i=1}^{n}(-1)^{i+1}a'_{i1}\det {M}'_{i}\\&=\det M+\det M'.\end{aligned}}$

Die Verträglichkeit mit der skalaren Multiplikation beweist man ähnlich, siehe Aufgabe *****.

$\Box$

 

Satz

Es sei ${}K$ ein Körper und ${}n\in \mathbb {N} _{+}$. Dann besitzt die Determinante

$\operatorname {Mat} _{n}(K)=(K^{n})^{n}\longrightarrow K,\,M\longmapsto \det M,$

folgende Eigenschaften.

1. Wenn in ${}M$ zwei Zeilen übereinstimmen, so ist ${}\det M=0$. D.h., dass die Determinante alternierend ist.
2. Wenn man in ${}M$ zwei Zeilen vertauscht, so ändert sich die Determinante mit dem Faktor ${}-1$.

Beweis

Dieser Beweis wurde in der Vorlesung nicht vorgeführt.

(1) und (2) werden parallel durch Induktion über ${}n$ bewiesen, wobei es für ${}n=1$ nichts zu zeigen gibt. Es sei also ${}n\geq 2$ und ${}M={\begin{pmatrix}v_{1}\\\vdots \\v_{n}\end{pmatrix}}=(a_{ij})_{ij}$. Die relevanten Zeilen seien ${}v_{r}$ und ${}v_{s}$ mit ${}r<s$. Nach Definition ist ${}\det M=\sum _{i=1}^{n}(-1)^{i+1}a_{i1}\det M_{i}$. Nach Induktionsvoraussetzung für (1) sind dabei ${}\det M_{i}=0$ für ${}i\neq r,s$, da ja dann zwei Zeilen übereinstimmen. Damit ist

${}\det M=(-1)^{r+1}a_{r1}\det M_{r}+(-1)^{s+1}a_{s1}\det M_{s}\,,$

wobei ${}a_{r1}=a_{s1}$ ist. Die beiden Matrizen ${}M_{r}$ und ${}M_{s}$ haben die gleichen Zeilen, allerdings tritt die Zeile ${}z=v_{r}=v_{s}$ in ${}M_{r}$ als die ${}(s-1)$-te Zeile und in ${}M_{s}$ als die ${}r$-te Zeile auf. Alle anderen Zeilen kommen in beiden Matrizen in der gleichen Reihenfolge vor. Durch insgesamt ${}s-r-1$ Vertauschungen von benachbarten Zeilen kann man ${}M_{r}$ in ${}M_{s}$ überführen. Nach der Induktionsvoraussetzung für (2) unterscheiden sich daher die Determinanten um den Faktor ${}(-1)^{s-r-1}$, also ist ${}\det M_{s}=(-1)^{s-r-1}\det M_{r}$. Setzt man dies oben ein, so erhält man

${}{\begin{aligned}\det M&=(-1)^{r+1}a_{r1}\det M_{r}+(-1)^{s+1}a_{s1}\det M_{s}\\&=a_{r1}{\left((-1)^{r+1}\det M_{r}+(-1)^{s+1}(-1)^{s-r-1}\det M_{r}\right)}\\&=a_{r1}{\left((-1)^{r+1}+(-1)^{2s-r}\right)}\det M_{r}\\&=a_{r1}{\left((-1)^{r+1}+(-1)^{r}\right)}\det M_{r}\\&=0.\end{aligned}}$

Jetzt beweisen wir (2). Nach Teil (1) (für ${}n$) und aufgrund der Multilinearität ist

${}{\begin{aligned}0&=\det {\begin{pmatrix}\vdots \\v_{r}+v_{s}\\\vdots \\v_{r}+v_{s}\\\vdots \end{pmatrix}}\\&=\det {\begin{pmatrix}\vdots \\v_{r}\\\vdots \\v_{r}+v_{s}\\\vdots \end{pmatrix}}+\det {\begin{pmatrix}\vdots \\v_{s}\\\vdots \\v_{r}+v_{s}\\\vdots \end{pmatrix}}\\&=\det {\begin{pmatrix}\vdots \\v_{r}\\\vdots \\v_{r}\\\vdots \end{pmatrix}}+\det {\begin{pmatrix}\vdots \\v_{r}\\\vdots \\v_{s}\\\vdots \end{pmatrix}}+\det {\begin{pmatrix}\vdots \\v_{s}\\\vdots \\v_{r}\\\vdots \end{pmatrix}}+\det {\begin{pmatrix}\vdots \\v_{s}\\\vdots \\v_{s}\\\vdots \end{pmatrix}}\\&=\det {\begin{pmatrix}\vdots \\v_{r}\\\vdots \\v_{s}\\\vdots \end{pmatrix}}+\det {\begin{pmatrix}\vdots \\v_{s}\\\vdots \\v_{r}\\\vdots \end{pmatrix}}.\end{aligned}}$

$\Box$

 

Satz

Es sei ${}K$ ein Körper und sei ${}M$ eine ${}n\times n$- Matrix über ${}K$. Dann sind die folgenden Aussagen äquivalent.

1. Es ist ${}\det M\neq 0$.
2. Die Zeilen von ${}M$ sind linear unabhängig.
3. ${}M$ ist invertierbar.
4. Es ist ${}\operatorname {rang} \,M=n$.

Beweis

Die Beziehung zwischen Rang, Invertierbarkeit und linearer Unabhängigkeit wurde schon in Korollar 26.4 gezeigt. Es seien die Zeilen linear abhängig. Wir können nach Zeilenvertauschungen annehmen, dass ${}v_{n}=\sum _{i=1}^{n-1}s_{i}v_{i}$ ist. Dann ist nach Satz 26.9 und Satz 26.10

${}\det M=\det {\begin{pmatrix}v_{1}\\\vdots \\v_{n-1}\\\sum _{i=1}^{n-1}s_{i}v_{i}\end{pmatrix}}=\sum _{i=1}^{n-1}s_{i}\det {\begin{pmatrix}v_{1}\\\vdots \\v_{n-1}\\v_{i}\end{pmatrix}}=0\,.$

Es seien nun die Zeilen linear unabhängig. Dann kann man durch Zeilenvertauschungen, Skalierung und Addition einer Zeile zu einer anderen Zeile die Matrix sukzessive zur Einheitsmatrix transformieren. Dabei ändert sich die Determinante stets durch einen von ${}0$ verschiedenen Faktor. Da die Determinante der Einheitsmatrix nach Lemma 26.8 gleich ${}1$ ist, muss auch die Determinante der Ausgangsmatrix ${}\neq 0$ sein.

$\Box$

Bemerkung  

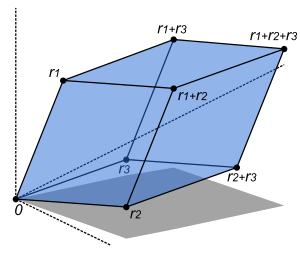
Bei ${}K=\mathbb {R}$ steht die Determinante in einer engen Beziehung zu Volumina von geometrischen Objekten. Wenn man im ${}\mathbb {R} ^{n}$ Vektoren ${}v_{1},\ldots ,v_{n}$ betrachtet, so spannen diese ein Parallelotop auf. Dieses ist definiert als

${}P:={\left\{s_{1}v_{1}+\cdots +s_{n}v_{n}\mid s_{i}\in [0,1]\right\}}\,.$

Es besteht also aus allen Linearkombinationen der Vektoren, wobei aber die Skalare auf das Einheitsintervall beschränkt sind. Wenn die Vektoren linear unabhängig sind, so handelt es sich wirklich um einen „voluminösen“ Körper, andernfalls liegt ein Objekt von niedrigerer Dimension vor. Es gilt nun die Beziehung

${}\operatorname {vol} \,P=\vert {\det {\left(v_{1},\ldots ,v_{n}\right)}}\vert \,,$

d.h. das Volumen des Parallelotops ist der Betrag der Determinante derjenigen Matrix, die entsteht, wenn man die aufspannenden Vektoren hintereinander schreibt.

Der Determinantenmultiplikationssatz und Folgerungen

Wir besprechen weitere wichtige Sätze über Determinanten, die wir aber nicht beweisen werden. Die Beweise beruhen auf einer systematischeren Untersuchung der für die Determinante charakteristischen Eigenschaften, multilinear und alternierend zu sein. Durch diese beiden Eigenschaften zusammen mit der Bedingung, dass die Determinante der Einheitsmatrix gleich ${}1$ ist, ist die Determinante nämlich schon eindeutig festgelegt.

Satz

Es sei ${}K$ ein Körper und ${}n\in \mathbb {N} _{+}$.

Dann gilt für Matrizen ${}A,B\in \operatorname {Mat} _{n}(K)$ die Beziehung

${}\det \left(A\circ B\right)=\det A\cdot \det B\,.$

Definition

Es sei ${}K$ ein Körper und sei ${}M={\left(a_{ij}\right)}_{ij}$ eine ${}m\times n$- Matrix über ${}K$. Dann nennt man die ${}n\times m$-Matrix

${M^{\text{tr}}}=(b_{ij})_{ij}{\text{ mit }}b_{ij}:=a_{ji}$

die transponierte Matrix zu ${}M$.

Die transponierte Matrix entsteht also, indem man die Rollen von Zeilen und Spalten vertauscht. Beispielsweise ist

${}{{\begin{pmatrix}t&n&o&e\\r&s&n&r\\a&p&i&t\end{pmatrix}}^{\text{tr}}}={\begin{pmatrix}t&r&a\\n&s&p\\o&n&i\\e&r&t\end{pmatrix}}\,.$

Satz

Es sei ${}K$ ein Körper und sei ${}M$ eine ${}n\times n$-Matrix über ${}K$.

Dann ist

${}\det M=\det {M^{\text{tr}}}\,.$

Daraus folgt, dass man die Determinante auch berechnen kann, indem man „nach einer Zeile entwickelt“, wie die folgende Aussage zeigt.

Korollar

Es sei ${}K$ ein Körper und sei ${}M={\left(a_{ij}\right)}_{ij}$ eine ${}n\times n$- Matrix über ${}K$. Zu ${}i,j\in {\{1,\ldots ,n\}}$ sei ${}M_{ij}$ diejenige Matrix, die entsteht, wenn man in ${}M$ die ${}i$-te Zeile und die ${}j$-te Spalte weglässt.

Dann ist (bei ${}n\geq 2$ für jedes feste ${}i$ bzw. ${}j$)

${}\det M=\sum _{i=1}^{n}(-1)^{i+j}a_{ij}\det M_{ij}=\sum _{j=1}^{n}(-1)^{i+j}a_{ij}\det M_{ij}\,.$

Beweis

Für ${}j=1$ ist die erste Gleichung die rekursive Definition der Determinante. Daraus folgt die Aussage für ${}i=1$ aufgrund von Satz 26.15. Durch Spalten- und Zeilenvertauschung folgt die Aussage daraus allgemein, siehe Aufgabe 26.12.

$\Box$

Die Determinante einer linearen Abbildung

Es sei

$\varphi \colon V\longrightarrow V$

eine lineare Abbildung eines Vektorraumes der Dimension ${}n$ in sich. Diese wird bezüglich einer Basis durch eine Matrix ${}M\in \operatorname {Mat} _{n}(K)$ beschrieben. Es liegt nahe, die Determinante dieser Matrix als Determinante der linearen Abbildung zu definieren, doch hat man hier das Problem der Wohldefiniertheit: die lineare Abbildung wird bezüglich einer anderen Basis durch eine „völlig“ andere Matrix beschrieben. Allerdings besteht zwischen den zwei beschreibenden Matrizen ${}M$ und ${}N$ und der Basiswechselmatrix ${}B$ aufgrund von Korollar 25.9 die Beziehung ${}N=BMB^{-1}$. Aufgrund des Determinantenmultiplikationssatzes ist daher

${}\det N=\det \left(BMB^{-1}\right)=(\det B)(\det M)(\det B^{-1})=(\det B)(\det B^{-1})(\det M)=\det M\,,$

so dass die folgende Definition in der Tat unabhängig von der Wahl einer Basis ist.

Definition

Es sei ${}K$ ein Körper und es sei ${}V$ ein endlichdimensionaler ${}K$- Vektorraum. Es sei

$\varphi \colon V\longrightarrow V$

eine lineare Abbildung, die bezüglich einer Basis durch die Matrix ${}M$ beschrieben werde. Dann nennt man

${}\det \varphi :=\det M\,$

die Determinante der linearen Abbildung ${}\varphi$.

<< | Kurs:Mathematik für Anwender (Osnabrück 2019-2020)/Teil I/Repetitorium | >> PDF-Version dieser Vorlesung Arbeitsblatt zur Vorlesung (PDF)