Kurs:Analysis/Teil II/19/Klausur mit Lösungen/kontrolle

Aufgabe	1	2	3	4	5	6	7	8	9	10	11	12	13	14	${}\sum$
Punkte	3	3	8	8	8	1	5	3	5	4	4	4	4	4	64

Aufgabe (3 Punkte)

Lösung

1. Unter einem euklidischen Vektorraum versteht man einen reellen endlichdimensionalen Vektorraum mit Skalarprodukt.
2. Die Menge aller Berührpunkte von ${}T$ heißt der Abschluss von ${}T$.
3. Es sei ${}I\subseteq \mathbb {R}$ ein offenes Intervall, ${}U\subseteq \mathbb {R} ^{n}$ offen und

   $h\colon I\times U\longrightarrow \mathbb {R}$

   eine Funktion. Dann nennt man den Ausdruck

   ${}y^{(n)}=h{\left(t,y,y',y^{\prime \prime },\ldots ,y^{(n-1)}\right)}\,$

   eine Differentialgleichung der Ordnung ${}n$.

4. Es sei

   ${}v'=Mv\,$

   mit

   ${}M\in \operatorname {Mat} _{n\times n}({\mathbb {K} })\,$

   eine lineare gewöhnliche Differentialgleichung mit konstanten Koeffizienten. Dann nennt man das charakteristische Polynom

   ${}\chi _{M}=\det {\left(tE_{n}-M\right)}\,$

   auch das charakteristische Polynom der Differentialgleichung.

5. Die Abbildung

   $\operatorname {Hess} _{P}\,f\colon \mathbb {R} ^{n}\times \mathbb {R} ^{n}\longrightarrow \mathbb {R} ,\,(u,v)\longmapsto D_{u}D_{v}f(P),$

   heißt die Hesse-Form im Punkt ${}P\in V$.

6. Die Faser über ${}y$ ist die Menge

   ${}F_{y}={\left\{x\in L\mid \varphi (x)=y\right\}}\,.$

Aufgabe (3 Punkte)

Lösung

1. Es sei ${}V$ ein reeller endlichdimensionaler Vektorraum. Es seien zwei Skalarprodukte ${}\left\langle -,-\right\rangle _{1}$ und ${}\left\langle -,-\right\rangle _{2}$ auf ${}V$ gegeben. Dann stimmen die über die zugehörigen Normen ${}\Vert {-}\Vert _{1}$ und ${}\Vert {-}\Vert _{2}$ definierten Topologien überein, d.h. eine Teilmenge ${}U\subseteq V$ ist genau dann offen bezüglich der einen Metrik, wenn sie offen bezüglich der anderen Metrik ist.
2. Es sei ${}\left\langle -,-\right\rangle$ eine symmetrische Bilinearform auf einem endlichdimensionalen reellen Vektorraum und sei ${}v_{1},\ldots ,v_{n}$ eine Basis von ${}V$. Es sei ${}G$ die Gramsche Matrix zu ${}\left\langle -,-\right\rangle$ bezüglich dieser Basis und es seien ${}D_{k}$ die Determinanten der quadratischen Untermatrizen

   $M_{k}=(\left\langle v_{i},v_{j}\right\rangle )_{1\leq i,j\leq k},\,k=1,\ldots ,n.$

   Dann gelten folgende Aussagen.

   1. Genau dann ist ${}\left\langle -,-\right\rangle$ positiv definit, wenn alle ${}D_{k}$ positiv sind.
   2. Genau dann ist ${}\left\langle -,-\right\rangle$ negativ definit, wenn das Vorzeichen in der Folge ${}D_{0}=1,\,D_{1},\,D_{2},\ldots ,D_{n}$ an jeder Stelle wechselt.
3. Es sei ${}U\subseteq \mathbb {R} ^{n}$ eine offene Teilmenge und sei

   $f\colon U\longrightarrow \mathbb {R} ^{m}$

   eine stetig differenzierbare Abbildung. Es sei ${}M=f^{-1}(b)$ die Faser von ${}f$ über ${}b\in \mathbb {R} ^{m}$. Es sei

   $h\colon U\longrightarrow \mathbb {R}$

   eine differenzierbare Funktion und die eingeschränkte Funktion ${}h{|}_{M}$ besitze im Punkt ${}a\in M$ ein lokales Extremum auf ${}M$ und ${}a$ sei ein regulärer Punkt von ${}f$. Dann ist

   ${}T_{a}M\subseteq \operatorname {kern} \left(Dh\right)_{a}\,,$

   d.h. die Linearform ${}\left(Dh\right)_{a}$ verschwindet auf dem Tangentialraum

   an der Faser von ${}f$ durch ${}a$.

Aufgabe (8 Punkte)

Beweise den Satz über die Charakterisierung von abgeschlossenen Mengen in einem metrischen Raum mit konvergenten Folgen.

Lösung

Es sei zunächst ${}T$ abgeschlossen und eine Folge ${}{\left(x_{n}\right)}_{n\in \mathbb {N} }\in T$ gegeben, die in ${}M$ gegen ${}x\in M$ konvergiert. Wir müssen zeigen, dass ${}x\in T$ ist. Angenommen, dies wäre nicht der Fall. Dann liegt ${}x$ im offenen Komplement von ${}T$ und daher gibt es ein ${}\epsilon >0$ derart, dass der gesamte ${}\epsilon$-Ball ${}U{\left(x,\epsilon \right)}$ im Komplement von ${}T$ liegt. Also ist

${}T\cap U{\left(x,\epsilon \right)}=\emptyset \,.$

Da die Folge aber gegen ${}x$ konvergiert, gibt es ein ${}n_{0}$ derart, dass alle Folgenglieder ${}x_{n}$, ${}n\geq n_{0}$, zu diesem Ball gehören. Da sie andererseits in ${}T$ liegen, ist dies ein Widerspruch.
  Es sei nun ${}T$ nicht abgeschlossen. Wir müssen eine Folge in ${}T$ konstruieren, die in ${}M$ konvergiert, deren Grenzwert aber nicht zu ${}T$ gehört. Da ${}T$ nicht abgeschlossen ist, ist das Komplement ${}U:=\setminus T$ nicht offen. D.h. es gibt einen Punkt ${}x\in U$ derart, dass in jedem ${}\epsilon$-Ball von ${}x$ auch Punkte außerhalb von ${}U$, also in ${}T$ liegen. Insbesondere ist also für jede natürliche Zahl ${}n\in \mathbb {N} _{+}$ der Durchschnitt

${}T\cap U{\left(x,{\frac {1}{n}}\right)}\neq \emptyset \,.$

Wir wählen aus dieser Schnittmenge ein Element ${}x_{n}$ und behaupten, dass die sich ergebende Folge die gewünschten Eigenschaften besitzt. Zunächst liegen nach Konstruktion alle Folgenglieder in ${}T$. Die Folge konvergiert gegen ${}x$, da man sich hierzu auf

${}\epsilon =1/n\,$

beschränken kann und alle Folgenglieder ${}x_{m}$, ${}m\geq n$, in ${}U{\left(x,{\frac {1}{m}}\right)}\subseteq U{\left(x,{\frac {1}{n}}\right)}$ liegen. Da der Grenzwert einer Folge im Falle der Existenz eindeutig bestimmt ist, und ${}x\notin T$ ist, konvergiert die Folge in ${}T$ nicht.

Aufgabe (8 (2+3+3) Punkte)

Es sei ${}M$ ein metrischer Raum und sei

$f\colon M\longrightarrow M$

eine Abbildung. Mit ${}f^{\circ n}$ bezeichnen wir die ${}n$-fache Hintereinanderschaltung von ${}f$ mit sich selbst.

a) Zeige, dass wenn ${}f$ Lipschitz-stetig ist, dass dann auch ${}f^{\circ n}$ Lipschitz-stetig ist.

b) Man gebe ein Beispiel für eine Lipschitz-stetige Abbildung ${}f$, die keine starke Kontraktion, wo aber jedes ${}f^{\circ n}$ für ${}n\geq 2$ eine starke Kontraktion ist.

c) Es sei ${}f$ Lipschitz-stetig und es sei ${}f^{\circ k}$ eine starke Kontraktion für ein gewisses ${}k$. Zeige, dass es ein ${}n_{0}$ derart gibt, dass ${}f^{\circ n}$ für jedes ${}n\geq n_{0}$ eine starke Kontraktion ist.

Lösung

a) Es sei ${}f$ Lipschitz-stetig mit Lipschitz-Konstante ${}L$. Es ist also

${}d(f(x),f(y))\leq Ld(x,y)\,$

für alle ${}x,y\in M$. Daher ist

${}d(f^{\circ n}(x),f^{\circ n}(y))\leq Ld(f^{\circ n-1}(x),f^{\circ n-1}(y))\leq \ldots \leq L^{n}d(x,y)\,$

und daher ist ${}f^{\circ n}$ Lipschitz-stetig mit Lipschitz-Konstante ${}L^{n}$.

b) Wir betrachten

$f\colon \mathbb {R} \longrightarrow \mathbb {R}$

mit

$f(x)={\begin{cases}0\,,{\text{ für }}x\leq 0\,,\\-2x\,,{\text{ für }}x>0\,.\end{cases}}$

Diese Funktion ist Lioschitz-stetig mit Lipschitz-Konstante ${}2$, die sich nicht verbessern lässt. Es liegt also keine starke Kontraktion vor. Da positive Zahlen auf negative Zahlen abgebildet werden und diese auf ${}0$, ist ${}f^{\circ 2}$ die Nullabbildung. Die höheren Hintereinanderschaltungen sind erst recht die Nullabbildung und dies ist eine starke Kontraktion.

c) Es sei ${}L$ eine Lipschitz-Konstante für ${}f$ und ${}c<1$ ein Kontraktionsfaktor für ${}f^{\circ k}$. Es sei ${}m$ so gewählt, dass

${}L^{k}c^{m}<1\,$

ist. Sei

${}n_{0}=mk\,.$

Für ${}n\geq n_{0}$ schreiben wir ${}n=ak+r$ mit ${}r<k$ und

${}f^{\circ n}=f^{\circ ak}\circ f^{\circ r}={\left(f^{\circ k}\right)}^{a}\circ f^{\circ r}\,.$

Da Lipschitz-Konstanten multiplikativ sind, gilt für diese Hintereinanderschaltung die Lipschitz-Konstante (${}L$ sei ${}\geq 1$)

${}c^{a}L^{r}\leq c^{a}L^{k}\leq c^{m}L^{k}<1\,.$

Es handelt sich also um starke Kontraktionen.

Aufgabe (8 (2+3+3) Punkte)

Wir betrachten einen Kreis (mit Radius ${}1$) und darin eingeschriebene regelmäßige ${}n$-Ecke.

1. 

   In den Kreis sei ein Quadrat eingeschrieben. Bestimme dessen Flächeninhalt und dessen Umfang.

2. 

   In den Kreis sei ein regelmäßiges ${}6$-Eck eingeschrieben. Bestimme dessen Flächeninhalt und dessen Umfang.

3. Der Flächeninhalt eines eingeschriebenen regelmäßigen ${}n$-Ecks ist eine Approximation für den Flächeninhalt des Kreises und der Umfang eines solchen ${}n$-Ecks ist eine Approximation für den Umfang des Kreises. Welche Approximationen sind besser?

Lösung

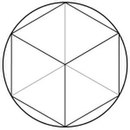
1. Die Seitenlänge des eingeschriebenen Quadrates ist nach dem Satz des Pythagoras gleich ${}{\sqrt {2}}$. Deshalb ist der Flächeninhalt des eingeschriebenen Quadrates gleich

   ${}{\sqrt {2}}\cdot {\sqrt {2}}=2\,$

   und der Umfang gleich ${}4{\sqrt {2}}$.

2. Das eingeschriebene regelmäßige Sechseck besteht aus ${}6$ gleichseitigen Dreiecken, da ja ihr Winkel im Kreismittelpunkt ${}60$ Grad beträgt, und somit ist ihre Seitenlänge gleich ${}1$. Die Höhe dieser Dreiecke ist nach dem Satz des Pythagoras gleich

   ${}{\sqrt {1-\left({\frac {1}{2}}\right)^{2}}}={\sqrt {\frac {3}{4}}}={\frac {\sqrt {3}}{2}}\,.$

   Der Flächeninhalt eines dieser Dreiecke ist

   ${}{\frac {1}{2}}\cdot 1\cdot {\frac {\sqrt {3}}{2}}={\frac {\sqrt {3}}{4}}\,,$

   somit ist der Flächeninhalt des eingeschriebenen Sechsecks gleich

   ${}6\cdot {\frac {\sqrt {3}}{4}}=3\cdot {\frac {\sqrt {3}}{2}}\,.$

   Der Umfang des Sechsecks ist ${}6$.

3. Das regelmäßige eingeschriebene ${}n$-Eck besteht aus ${}n$ gleichen gleichschenkligen Dreiecken, deren Schenkel die Länge ${}1$ haben. Deren Grundseite sei mit ${}g_{n}$ und deren Höhe sei mit ${}h_{n}$ bezeichnet (deren Werte muss man für den Vergleich der Approximationen nicht ausrechnen). Der Flächeninhalt eines solchen Dreiecks ist ${}{\frac {1}{2}}g_{n}h_{n}$ und somit ist der Flächeninhalt des eingeschriebenen ${}n$-Ecks gleich

   $n{\frac {1}{2}}g_{n}h_{n}.$

   Der Umfang des ${}n$-Ecks ist

   $ng_{n}.$

   Das Verhältnis des Flächeninhalts des ${}n$-Ecks zum Flächeninhalt des Kreises ist somit

   ${}{\frac {n{\frac {1}{2}}g_{n}h_{n}}{\pi }}=h_{n}{\frac {ng_{n}}{2\pi }}\,,$

   das Verhältnis des Umfangs des ${}n$-Ecks zum Umfang des Kreises ist

   ${\frac {ng_{n}}{2\pi }}.$

   Wegen ${}h_{n}<1$ ist die Umfangsapproximation besser als die Flächenapproximation.

Aufgabe (1 Punkt)

Skizziere den Graphen der Addition

$+\colon \mathbb {R} \times \mathbb {R} \longrightarrow \mathbb {R} ,\,(x,y)\longmapsto x+y.$

Lösung Graph (Abbildung)/R/Addition/Aufgabe/Lösung

Aufgabe (5 Punkte)

Bestimme die Lösung des Anfangswertproblems

${}{\begin{pmatrix}x\\y\\z\end{pmatrix}}'={\begin{pmatrix}5&0&t\\0&-3&0\\0&0&1\end{pmatrix}}{\begin{pmatrix}x\\y\\z\end{pmatrix}}\,$

mit der Anfangsbedingung

${}{\begin{pmatrix}x(0)\\y(0)\\z(0)\end{pmatrix}}={\begin{pmatrix}1\\1\\1\end{pmatrix}}\,.$

Lösung

${}{\begin{pmatrix}x\\y\\z\end{pmatrix}}'={\begin{pmatrix}5&0&t\\0&-3&0\\0&0&1\end{pmatrix}}{\begin{pmatrix}x\\y\\z\end{pmatrix}}\,$

Aus der dritten Zeile

${}z'=z\,$

mit der Anfangsbedingung ${}z(0)=1$ folgt direkt

${}z(t)=e^{t}\,.$

Entsprechend folgt aus der zweiten Zeile direkt

${}y(t)=e^{-3t}\,.$

Die erste Zeile liefert die eindimensionale Differentialgleichung

${}x'=5x+te^{t}\,.$

Dies ist eine eindimensionale inhomogene lineare Differentialgleichung. Die zugehörige homogene Gleichung besitzt die Lösung ${}e^{5t}$. Mit Variation der Konstanten, also dem Ansatz

${}x(t)=c(t)e^{5t}\,$

(siehe Satz 29.10 (Analysis (Osnabrück 2021-2023))), ergibt sich die Bedingung

${}c'(t)=te^{t}\cdot e^{-5t}=te^{-4t}\,.$

Die Stammfunktion hiervon sind

$-{\frac {1}{4}}te^{-4t}-{\frac {1}{16}}e^{-4t}+c.$

Somit ist

${}x(t)={\left(-{\frac {1}{4}}te^{-4t}-{\frac {1}{16}}e^{-4t}+c\right)}e^{5t}\,$

und die Anfangsbedingung legt

${}c={\frac {17}{16}}\,$

fest. Die Lösung des Anfangswertproblems ist somit

${}{\begin{aligned}{\begin{pmatrix}x(t)\\y(t)\\z(t)\end{pmatrix}}&={\begin{pmatrix}{\left(-{\frac {1}{4}}te^{-4t}-{\frac {1}{16}}e^{-4t}+{\frac {17}{16}}\right)}e^{5t}\\e^{-3t}\\e^{t}\end{pmatrix}}\\&={\begin{pmatrix}-{\frac {1}{4}}te^{t}-{\frac {1}{16}}e^{t}+{\frac {17}{16}}e^{5t}\\e^{-3t}\\e^{t}\end{pmatrix}}.\end{aligned}}$

Aufgabe (3 Punkte)

Es sei ${}f\colon \mathbb {R} ^{3}\rightarrow \mathbb {R}$ eine dreimal stetig differenzierbare Funktion. Zeige

${}{\frac {\partial }{\partial z}}{\frac {\partial }{\partial y}}{\frac {\partial }{\partial x}}f={\frac {\partial }{\partial x}}{\frac {\partial }{\partial y}}{\frac {\partial }{\partial z}}f\,.$

Lösung

Unter mehrfacher Anwendung des Satzes von Schwarz ist (die Klammern verdeutlichen, wie der Satz angewendet wird. Für die vierte Gleichung wird verwendet, dass ${\frac {\partial }{\partial y}}f$ zweimal stetig differenzierbar ist)

${}{\begin{aligned}{\frac {\partial }{\partial z}}{\frac {\partial }{\partial y}}{\frac {\partial }{\partial x}}f&={\frac {\partial }{\partial z}}{\left({\frac {\partial }{\partial y}}{\frac {\partial }{\partial x}}f\right)}\\&={\frac {\partial }{\partial z}}{\left({\frac {\partial }{\partial x}}{\frac {\partial }{\partial y}}f\right)}\\&={\left({\frac {\partial }{\partial z}}{\frac {\partial }{\partial x}}\right)}{\left({\frac {\partial }{\partial y}}f\right)}\\&={\left({\frac {\partial }{\partial x}}{\frac {\partial }{\partial z}}\right)}{\left({\frac {\partial }{\partial y}}f\right)}\\&={\frac {\partial }{\partial x}}{\left({\frac {\partial }{\partial z}}{\frac {\partial }{\partial y}}f\right)}\\&={\frac {\partial }{\partial x}}{\left({\frac {\partial }{\partial y}}{\frac {\partial }{\partial z}}f\right)}\\&={\frac {\partial }{\partial x}}{\frac {\partial }{\partial y}}{\frac {\partial }{\partial z}}f.\end{aligned}}$

Aufgabe (5 Punkte)

Beweise den Satz über totale Differenzierbarkeit und Richtungsableitungen.

Lösung

Da ${}\left(D\varphi \right)_{P}$ eine lineare Abbildung von ${}V$ nach ${}W$ ist, liefert die Anwendung dieser Abbildung auf einen Vektor ${}v\in V$ einen Vektor in ${}{\left(D\varphi \right)}_{P}{\left(v\right)}\in W$. Nach Voraussetzung haben wir

${}\varphi (P+v)=\varphi (P)+{\left(D\varphi \right)}_{P}{\left(v\right)}+\Vert {v}\Vert \cdot r(v)\,$

(mit den üblichen Bedingungen an ${}r$). Insbesondere gilt für (hinreichend kleines) ${}s\in {\mathbb {K} }$

${}\varphi (P+sv)=\varphi (P)+s{\left(D\varphi \right)}_{P}{\left(v\right)}+\vert {s}\vert \cdot \Vert {v}\Vert \cdot r(sv)\,.$

Also gilt

${}{\begin{aligned}\operatorname {lim} _{s\rightarrow 0,s\neq 0}\,{\frac {\varphi (P+sv)-\varphi (P)}{s}}&=\operatorname {lim} _{s\rightarrow 0,s\neq 0}\,{\frac {s{\left(D\varphi \right)}_{P}{\left(v\right)}+\vert {s}\vert \cdot \Vert {v}\Vert \cdot r(sv)}{s}}\\&=\operatorname {lim} _{s\rightarrow 0,s\neq 0}\,\left({\left(D\varphi \right)}_{P}{\left(v\right)}+{\frac {\vert {s}\vert }{s}}\Vert {v}\Vert \cdot r(sv)\right)\\&={\left(D\varphi \right)}_{P}{\left(v\right)},\end{aligned}}$

da ${}\operatorname {lim} _{s\rightarrow 0}\,r(sv)=0$ und der Ausdruck ${}{\frac {\vert {s}\vert }{s}}\Vert {v}\Vert$ beschränkt ist.

Aufgabe (4 (1+1+1+1) Punkte)

Wie betrachten die komplexe Invertierung

$f\colon {\mathbb {C} }\setminus \{0\}\longrightarrow {\mathbb {C} },\,z\longmapsto z^{-1}.$

1. Bestimme die Ableitung ${}f'(z)$ von ${}f$.
2. Beschreibe die Funktion

   $f\colon \mathbb {R} ^{2}\setminus \{0\}\longrightarrow \mathbb {R} ^{2}$

   mit den reellen Koordinaten ${}x,y$ (bezüglich der reellen Basis ${}1$ und ${}{\mathrm {i} }$ von ${}{\mathbb {C} }$).

3. Bestimme das totale Differential zu ${}f$ bezüglich der Basis ${}1$ und ${}{\mathrm {i} }$ in einem beliebigen Punkt.
4. Beschreibe die Multiplikation mit ${}f'(z)$ auf ${}{\mathbb {C} }$ durch eine reelle Matrix bezüglich der reellen Basis ${}1$ und ${}{\mathrm {i} }$.

Lösung

1. Die Ableitung ist

   ${}f'(z)=-{\frac {1}{z^{2}}}\,.$

2. In reellen Koordinaten ist die Abbildung durch

   $z=x+{\mathrm {i} }y\longmapsto {\frac {x}{x^{2}+y^{2}}}-{\mathrm {i} }{\frac {y}{x^{2}+y^{2}}}$

   gegeben.

3. Das totale Differential der Abbildung aus (2) ist

   ${}{\begin{pmatrix}{\frac {(x^{2}+y^{2})-2x^{2}}{(x^{2}+y^{2})^{2}}}&{\frac {-2xy}{(x^{2}+y^{2})^{2}}}\\{\frac {2xy}{(x^{2}+y^{2})^{2}}}&{\frac {-(x^{2}+y^{2})+2y^{2}}{(x^{2}+y^{2})^{2}}}\end{pmatrix}}={\begin{pmatrix}{\frac {-x^{2}+y^{2}}{(x^{2}+y^{2})^{2}}}&{\frac {-2xy}{(x^{2}+y^{2})^{2}}}\\{\frac {2xy}{(x^{2}+y^{2})^{2}}}&{\frac {-x^{2}+y^{2}}{(x^{2}+y^{2})^{2}}}\end{pmatrix}}\,.$

4. Es ist für ${}z=x+{\mathrm {i} }y$

   ${}{\begin{aligned}f'(z)&=-{\frac {1}{z^{2}}}\\&=-{\frac {1}{\left(x+{\mathrm {i} }y\right)}}\cdot {\frac {1}{\left(x+{\mathrm {i} }y\right)}}\\&=-{\frac {\left(x-{\mathrm {i} }y\right)}{x^{2}+y^{2}}}\cdot {\frac {\left(x-{\mathrm {i} }y\right)}{x^{2}+y^{2}}}\\&=-{\frac {{\left(x-{\mathrm {i} }y\right)}^{2}}{{\left(x^{2}+y^{2}\right)}^{2}}}\\&=-{\frac {x^{2}-y^{2}-2{\mathrm {i} }xy}{{\left(x^{2}+y^{2}\right)}^{2}}}\\&={\frac {-x^{2}+y^{2}+2{\mathrm {i} }xy}{{\left(x^{2}+y^{2}\right)}^{2}}}.\end{aligned}}$

   Die Multiplikation mit ${}1$ ist eben diese Zahl, die Multiplikation mit ${}{\mathrm {i} }$ ist

   ${\frac {{\left(-x^{2}+y^{2}\right)}{\mathrm {i} }-2xy}{{\left(x^{2}+y^{2}\right)}^{2}}}.$

   Dies führt zur gleichen Matrix wie in Teil (3).

Aufgabe (4 Punkte)

Es sei ${}\left\langle -,-\right\rangle$ eine Bilinearform auf einem zweidimensionalen reellen Vektorraum, die bezüglich einer Basis durch die Gramsche Matrix

${\begin{pmatrix}0&b\\b&c\end{pmatrix}}$

beschrieben werde. Bestimme den Typ der Form in Abhängigkeit von ${}b,c$.

Lösung

Wir verwenden das Eigenwertkriterium. Das charakteristische Polynom der Matrix ist

${}X(X-c)-b^{2}=X^{2}-cX-b^{2}\,.$

Bei ${}b\neq 0$ ist der Wert des charakteristischen Polynoms an der Stelle ${}0$ negativ. Somit gibt es eine negative und eine positive Nullstelle und daher ist der Typ gleich ${}(1,1)$. Es sei also ${}b=0$. Die Nullstellen des charakteristischen Polynoms sind dann ${}0$ und ${}c$. Bei ${}c=0$ liegt die Nullform mit dem Typ ${}(0,0)$ vor. Bei negativem ${}c$ ist der Typ ${}(0,1)$ und bei positivem ${}c$ ist der Typ ${}(1,0)$.

Aufgabe (4 Punkte)

Bestimme die kritischen Punkte der Funktion

$\varphi \colon \mathbb {R} ^{2}\longrightarrow \mathbb {R} ,\,(x,y)\longmapsto 3x^{2}-2xy-y^{2}+5x,$

und entscheide, ob in diesen kritischen Punkten ein lokales Extremum vorliegt.

Lösung

Die Jacobi-Matrix dieser Funktion ist

$(6x-2y+5,-2x-2y).$

Wir setzen beide Komponenten gleich ${}0$ und erhalten durch Subtraktion der beiden Gleichungen voneinander die Bedingung

$8x+5=0,$

also ist

$x=-{\frac {5}{8}}{\text{ und daher }}y={\frac {5}{8}}.$

Der einzige kritische Punkt der Funktion ist also

${}P=\left(-{\frac {5}{8}},\,{\frac {5}{8}}\right)\,.$

Wir bestimmen die Hesse-Matrix in diesem Punkt. Sie ist

${\begin{pmatrix}6&-2\\-2&-2\end{pmatrix}}.$

Wir wenden das Minorenkriterium an. Der Eintrag links oben ist positiv, die Determinante ist ${}-12-4=-16$, also negativ. Daher besitzt die Hesse-Form den Typ ${}(1,1)$, und somit liegt kein lokales Extremum vor.

Aufgabe (4 Punkte)

Man gebe für jedes ${}n\in \mathbb {N} _{+}$ eine bijektive, total differenzierbare Abbildung

$\varphi _{n}\colon \mathbb {R} ^{n}\longrightarrow \mathbb {R} ^{n}$

an, für die das totale Differential in mindestens einem Punkt nicht regulär ist.

Lösung

Für ${}n=1$ ist die Abbildung

$\mathbb {R} \longrightarrow \mathbb {R} ,\,x\longmapsto x^{3},$

bijektiv (mit der Umkehrfunktion ${}x\mapsto {\sqrt[{3}]{x}}$). Für ein ${}n\in \mathbb {N} _{+}$ betrachten wir die Abbildung

$\varphi _{n}\colon \mathbb {R} ^{n}\longrightarrow \mathbb {R} ^{n},\,(x_{1},x_{2},\ldots ,x_{n})\longmapsto (x_{1}^{3},x_{2},\ldots ,x_{n}).$

Dies ist eine polynomiale Abbildung, sodass das totale Differential durch die Jacobi-Matrix, also durch

${\begin{pmatrix}3x_{1}^{2}&0&\cdots &0\\0&1&\ddots &\vdots \\\vdots &\ddots &\ddots &0\\0&\cdots &0&1\end{pmatrix}}$

gegeben ist. Für ${}x_{1}=0$ ist diese Matrix nicht invertierbar, da ihre Determinante ${}0$ ist, und die Abbildung ist für diese Punkte nicht regulär. Dennoch ist die Abbildung bijektiv, die Umkehrabbildung wird durch

$\mathbb {R} ^{n}\longrightarrow \mathbb {R} ^{n},\,(x_{1},x_{2},\ldots ,x_{n})\longmapsto ({\sqrt[{3}]{x_{1}}},x_{2},\ldots ,x_{n})$

gegeben.

Aufgabe (4 Punkte)

Beweise den Satz über das Wegintegral in einem Gradientenfeld.

Lösung

Aufgrund der Kettenregel ist

${}{\begin{aligned}\int _{\gamma }G&=\int _{a}^{b}\left\langle G(\gamma (t)),\gamma '(t)\right\rangle dt\\&=\int _{a}^{b}\sum _{i=1}^{n}G_{i}(\gamma (t))\cdot \gamma _{i}'(t)dt\\&=\int _{a}^{b}\sum _{i=1}^{n}{\frac {\partial h}{\partial x_{i}}}(\gamma (t))\cdot \gamma _{i}'(t)dt\\&=\int _{a}^{b}(h\circ \gamma )^{\prime }(t)dt\\&=h(\gamma (b))-h(\gamma (a)).\end{aligned}}$